Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

MECHANICAL SYSTEMS, CLASSICAL MODELS

()

(), () (0)xxδϕ ϕ.

(1.1.29)

We can define the Dirac distribution also on the space

K ; it will be called, in this case,

the Dirac measure.

If the fundamental functions

∈

Kϕ are defined in

R , then we have

()

12 12

( , ,..., ), ( , ,..., ) (0, 0,...,0)

xx x xx xδϕ ϕ.

(1.1.29')

The relation

(

)

(

)

−= +

(),()(),()

xx x fx xxϕϕ,

∈

xx R ,

(1.1.30)

defines a

translated distribution

−

()

xx. In particular, for the Dirac distribution

−

()xxδ we may write

()

−=

(),()()xx x xδϕϕ,

∈

xx R .

(1.1.30')

For distributions subjected to a

homothetic transformation with respect to the

independent variable, we shall use – by definition – the formula

()

(

)

(

)

−

(),() (),

xx fx xαϕ α ϕ

∈

x R .

(1.1.31)

For

=−1α we obtain the property of symmetry and we may write

()

(

)

−=−(),() (),()

xx fx xϕϕ,

∈

x R .

(1.1.32)

In particular, we observe that

−

=() ()xxδδ, hence the Dirac distribution is even with

respect to the independent variable

∈

x R .

The equality of two distributions

()

x and ()gx is defined by the relation

(

)

(

)

gϕϕ,

∀

∈ Kϕ ;

(1.1.33)

hence, we may write

g .

(1.1.33')

A distribution

()

x is equal to zero

(

)

if, for any fundamental function ()xϕ ,

we have

()

=(), () 0

xxϕ . If the distributions

and

are generated by continuous

functions

()

x and ()gx , then the equality (1.1.33') occurs in the usual sense, i.e.

punctual, because – in this case – the distributions

and g coincide everywhere with

the functions

and

. If the functions

and

are locally integrable and coincide

almost everywhere, then the distributions generated by them will be equal and relation

(1.1.33') holds.

Newtonian model of mechanics

We define

the Heaviside function (the unit function) on the real axis in the form

(Fig.1.9)

⎧

⎪

⎨

≥

⎪

⎩

0, 0,

()

1, 0;

(1.1.34)

the distribution generated by it will be called

the Heaviside distribution. If ()

x is a

function of variable

x , defined on the real axis, then we will call its positive part the

function

defined by the relation (Fig.1.10,a)

Figure 1.9. The Heaviside function. Figure 1.10. The positive part of function ()fx (a) and

of function

()fx x= (b).

⎧

⎪

⎨

≥

⎪

⎩

0, 0,

() ()()

(), 0.

fx fx x

fx x

(1.1.35)

In particular, for the function

()

xx we can introduce the positive part (Fig.1.10,b)

⎧

⎪

⎨

≥

⎪

⎩

0, 0,

()

, 0;

xxx

(1.1.36)

obviously, to these functions correspond certain distributions of function type. We

introduce also the distribution generated by the function

=1( ) 1x , ∀∈x R

(Fig.1.11).

Figure 1.11. The function 1( ) 1x = . Figure 1.12. The characteristic function.

The characteristic function corresponding to the interval

−

[,]aa is defined in the form

(Fig.1.12)

MECHANICAL SYSTEMS, CLASSICAL MODELS

⎧

⎪

⎨

≤

⎪

⎩

0, ,

()

1, ,

> 0a ,

(1.1.37)

being thus led to a distribution of function type; this distribution may be expressed also

by the Heaviside distribution

=+−−=−() ( ) ( ) ( )hx x a x a a xθθ θ,

∈

x R .

(1.1.37')

()xψ is a function of class C

∞

, then we can write the equality

()() (0)()xx xψδ ψδ ;

(1.1.38)

in particular, for

=()

xxψ , we obtain

() 0

xxδ ,

(1.1.39)

so that the product of a distribution by a function indefinite differentiable may be equal

to zero, even if no one of its factors vanishes. Analogously,

−

=−()( ) ()( )xxa axaψδ ψδ .

(1.1.38')

We mention also the decomposition formula of a distribution

()

[]

−= −−+

()()

xa xa xa

δδδ

, > 0a ;

(1.1.40)

using formula (1.1.38'), we may write

(

)

++ −= −

()()2xa xa ax aδδ δ , > 0a .

(1.1.40')

We also have

[

]

−+ −=− − −()() ()()xa xb ab xaxbδδ δ .

(1.1.41)

R we obtain

()

()()

[

−−= −−++−

2222

1122 1122 1122

,,,

xaxa xaxa xaxa

δδδ

(

)

(

)

]

+− ++ + +

1122 1122

,,xaxa xaxaδδ, >,0ab .

(1.1.42)

We mention also formula (in

R )

() ( )

⎡⎤

−−−=−−−

⎣⎦

20 0 0 0 0 0

1 1 1 2 23 3 1 12 23 3

2,, ,,x x x x xx x x xx xx xδδ

()

−+ − −

000

112233

,,xxxxxxδ .

(1.1.43)

Newtonian model of mechanics

We call

support of the distribution

( supp

) the complement of the union of open

sets on which this distribution vanishes; therefore, the support of a distribution is a

closed set. If the support of a distribution is contained in a set

A , then we say that the

distribution is

concentrated on the set A . Thus, we may say that the Dirac distribution

()xδ is concentrated at a point (the origin). Analogously, one can define distributions

concentrated on curves or surfaces, in general distributions concentrated on a manifold

of a space

R .

Figure 1.13. A δ representative sequence.

We say that a sequence of functions

(

)

, ,...,

xx x is a δ representative

sequence

if, in the sense of the topology of K

′

is the topological dual of K ,

containing the distributions defined on this fundamental space) we have (in Fig.1.13

is given a

δ representative sequence for

1m )

()

(

)

→∞

12 12

lim , ,..., , ,...,

nm m

xx x xx xδ ;

(1.1.44)

obviously, this condition is equivalent to

()

(

)()

()

→∞

12 12

lim , ,..., , , ,..., 0,0,..., 0

nm m

xx x xx xϕϕ

(1.1.44')

From the very beginning, we mention that

the distributions admit derivatives of any

order

, which is a great advantage with respect to usual functions. Let ()

x be a

function of class

C and ()xϕ a fundamental function belonging to the fundamental

space

K ; considering the corresponding distribution of function type, we obtain the

rule of differentiation

in the form

(

)

(

)

fϕϕ

′

− .

(1.1.45)

In particular, we have

() ()xxθδ

′

(1.1.46)

MECHANICAL SYSTEMS, CLASSICAL MODELS

In case of a distribution of several variables

(

)

, ,...,

xx x , we can write

()()

∂

⎛⎞

⎜⎟

∂

⎝⎠

12 12

, ,..., , , ,...,

fxx x xx x

()()

∂

⎛⎞

=−

⎜⎟

∂

⎝⎠

12 12

, ,..., , , ,...,

fxx x xx x

ϕ ,

1,2,...,in;

(1.1.47)

one obtains also the property

∂∂

∂∂ ∂∂

ij ji

xx x x

, 1,2,...,ij n,

(1.1.48)

which shows that, in case of distributions, the derivatives do not depend on the order of

differentiation.

Let

()

x be a function of class

C everywhere, excepting at the point

x , where the

function has a discontinuity of the first species, the corresponding

jump being given by

=+−−

00 0

(0)(0)sfx fx .

(1.1.49)

We denote by

()

′

the derivative of the distribution ()

x (in the sense of the theory

of distributions

) and by ()

′



the distribution corresponding to the derivative of the

function, which generated the distribution

, in the usual sense, wherever this derivative

exists; we obtain the relation

() () ( )

xfxsxxδ

′′

=+−



(1.1.50)

It is worth to note that if the function

()

x is continuous at the point

x , then the jump

s vanishes, and formula (1.1.50) becomes

() ()

xfx

′



;

(1.1.50')

i.e., the derivative in the sense of the theory of distributions coincides with the

derivative in the usual sense.

If the function

()

x is of class

C everywhere excepting the points

x ,

= 1,2,...,in

, where it has discontinuities of the first species and if we denote by

the jump of the function at the point

x , then, by a similar procedure, we obtain a more

general formula, namely

() () ( )

xfx sxxδ

′′

=+ −

∑



(1.1.51)

A last property, which is worth to be revealed, is the following:

If the derivative of a

distribution is equal to zero, then the distribution is a constant

Newtonian model of mechanics

Let

()

x be a continuous function on [, ]ab , and ()gx a function with an integrable

derivative on the same interval; one can show that, in this case,

the Stieltjes integral

()d()

xgx

∫

exists, its computation being reduced to the computation of a Riemann

integral

' () ()d() () ()()d

SfxgxRfxgxx=

∫∫

(1.1.52)

It is important to mention that, in general, the symbol

d()gx which appears in the

Stieltjes integral does not represent

the differential of the function ()gx ; the fact that the

function

()gx has an integrable derivative in the conditions mentioned above allows us

to admit that

d()gx is the differential of ()gx in the formula (1.1.52), hence one can

pass easily from the Stieltjes integral to the Riemann one. If

()

x and ()gx are

distributions and the Stieltjes integral does exist, then the symbol

d()gx can be also

considered as a

differential in the sense of the theory of distributions; in this case, if

()

x is a continuous function on [,]ab , excepting a finite number of points

...

ac c c c b=<<<< =, where there are discontinuities of the first species,

then there exists the Stieltjes integral and the relation

[]

() ()d() () ()()d () ( 0) ()

SfxgxRfxgxxfaga ga

′

=++−

∫∫

[][]

−

++−−+−−

∑

()( 0)( 0) ()()(0)

kk k

fc gc gc fb gb gb

(1.1.53)

holds.

Analogously, if

(, )

xx is a continuous function in a two-dimensional interval Δ

and if the function

(, )gx x is a non-decreasing function with respect to each variable

and has the property

Δ≡++−+−+

2 12 1 12 2 1 12 12 2

(,)(,)(,)(,)gx x gx h x h gx h x gx x h

(, ) 0gx x+≥,

∀

,0hh ,

(1.1.54)

then

the double Stieltjes integral

12 2 12

(, )D(, )fx x gx x

∫∫

exists. If the function

(, )gx x admits second order continuous partial derivatives, then the computation of

the double Stieltjes integral reduces to the computation of a

double Riemann integral

12 2 12 12

() (, )D(, ) () (, )SfxxgxxRfxx

ΔΔ

∫∫ ∫∫

′

12 1 2

(, )dd

gxxxx;

(1.1.55)

this result remains valid if, instead of the continuity of the mixed derivative

′′

(, )

gxx, its integrability only is asked. On the basis of this theorem, one can pass

from the double Stieltjes integral to the double Riemann integral directly if, instead of

MECHANICAL SYSTEMS, CLASSICAL MODELS

the symbol

212

D(, )gx x one considers the expression

′

12 1 2

(, )dd

gxxxx. In fact, the

symbol

212

D(, )gx x represents a differential operator specific to the double Stieltjes

integral, which is nothing else than

the two-dimensional differential of the function

(, )gx x ; we mention also that

′

(, )

gxx represents the two-dimensional

derivative

of this function. We can write

′

212 12 12

D(, ) (, )dd

gx x g x x x x .

(1.1.56)

If the function

(, )

xx defined on Δ is continuous, then we have

00 00

12 2 1 1 2 2 1 2

() ( , )D ( , ) ( , )Sfxx xxxxfxx

θ −−=

∫∫

(1.1.57)

Let be the function

(, )gx x of the form

()

=+ −−

∑

() ()

12 12 1 2

(, ) (, ) ,

gx x gx x g x x x xθ



(1.1.58)

where

g are constants and

(, )gx x



is the continuous part of the function

(, )gx x

Δ ; taking into account the relations (1.1.55), (1.1.57) as well as the property of

additivity of the Stieltjes integral, we get

12 2 12 12

() (, )D(, ) () (, )SfxxgxxRfxx

ΔΔ

∫∫ ∫∫

12 1 2

(, )dd

gxxxx

′



()

∑

() ()

gf x x .

(1.1.59)

We may write also the relation

()

=+ −−

∑

() ()

212 2 12 2 1 2

D(, ) D (, ) D ,

gxx gxx g xxxxθ



(1.1.60)

or the relation

()

=+Δ−−

∑

() ()

212 12 1 2 12

D(,)D(,) , dd

gxx gxx g xxxx xxδ ,

(1.1.61)

where

212

D(, )gx x and

D(, )gx x represent the two-dimensional differentials in

the sense of the theory of distributions

and in the usual sense, respectively, while

()

(

)

() () () ()

12 12

0, 0 0, 0

kk kk

ggx x gx xΔ= + +− + −

()

(

)

() () () ()

12 12

0, 0 0, 0

kk kk

gx x gx x−−++ −−

(1.1.61')

Newtonian model of mechanics

the two-dimensional jump of the function

(, )gx x at the point of discontinuity

()

() ()

xx , = 1,2,...,kn.

Let

123

(, , )gx x x be a non-decreasing function with respect to each variable, defined

on a three-dimensional interval

Δ , and which verifies the inequality

(

)( )

(

)

Δ≡+++−++

3 123 1 12 23 3 12 23 3

,, , , , ,gx x x gx h x h x h gx x h x h

(

)

(

)

(

)

−+ +− + + + +

1123 3 11223 1123

,, , , ,,gx hxx h gx hx hx gx hx x

()

(

)

(

)

+++ +− ≥

12 23 123 3 123

,, ,, ,,0gx x h x gx x x h gx x x ,

∀

123

,, 0hhh ;

(1.1.62)

123

(,, )

xxx is a continuous function on Δ , then the triple Stieltjes integral

()()

∫∫∫

123 3 123

,, D ,,fxx x gxx x

does exist. If the function

123

(, , )gx x x admits

continuous partial derivatives of third order, then the triple Stieltjes integral is reduced

to a

triple Riemann integral

()()

123 3 123

() , , D , ,Sfxxxgxxx

∫∫∫

()

123

() , ,Rfxxx

∫∫∫

(

)

′

′′

123

123 1 2 3

,, ddd

xxx

gxxxxxx.

(1.1.63)

Hence, in the above-mentioned conditions, one may pass directly from the Stieltjes

integral to the Riemann one, admitting the relation

()

(

)

′

′′

123

3123 123 123

D,, ,,ddd

xxx

gx x x g x x x x x x;

(1.1.64)

()

3123

D,,gx x x represents here the three-dimensional differential of the function

()

123

,,gx x x , while

(

)

′′′

123

xxx

gxxx is the three-dimensional derivative of this

function. As in the case of the one- or two-dimensional Stieltjes integral, if

()

123

xxx and

()

123

,,gx x x are distributions for which the product

()

123

xxx

()

⋅

3123

D,,gx x x makes sense, then this interpretation is always possible. Introducing

the Heaviside function, one can show that

()

(

)

(

)

000 000

123 3 1 1 2 2 3 3 1 2 3

() , , D , , , ,S fxxx x xx xx x fxxx

θ −−−=

∫∫∫

(1.1.65)

where

()

123

xxx is a continuous function on Δ . Let be now the function

()()

()

=+−−−

∑

() () ()

123 123 1 2 3

123

,, ,, , ,

kkk

gxxx gxxx gxxxxxxθ



(1.1.66)

where

g are constants, while

(

)

123

,,gx x x



is the continuous part of this function; one

may show that

MECHANICAL SYSTEMS, CLASSICAL MODELS

()()

123 3 123

() , , D , ,Sfxxxgxxx

∫∫∫

()

123

() , ,Rfxxx

∫∫∫

(

)

′

′′

123

123 1 2 3

,, ddd

xxx

gxxxxxx

()

∑

() () ()

123

kkk

gfxxx

(1.1.67)

It results

()()

()

=+−−−

∑

() () ()

3 123 3 123 3 1 2 3

123

D,, D ,, D , ,

kkk

gxxx gxxx g xxxxxxθ



;

(1.1.68)

we can also write

()

3123 123

D,, D,,gx x x gx x x

()

+Δ − − −

∑

() () ()

123 123

123

,, ddd

kkk

g xxxxxx xxxδ ,

(1.1.69)

where we have put in evidence

the three-dimensional differentials in the sense of the

theory of distributions

and in the usual sense, respectively, as well as the three-

dimensional jumps

()

g of the function

(

)

123

,,gx x x at the points of discontinuity

(

)

() ()

()

, ,

xxx , = 1,2,...,kn.

1.1.8 Mechanical systems

The mathematical models of bodies have frequently ideal characteristics; one may

thus consider

material points (without dimension), material lines (one-dimensional

manifolds), or

material surfaces (two-dimensional manifolds) in the space

. For

example, a body whose dimensions are negligible with respect to the dimensions which

appear in the considered problem (a planet with respect to the dimensions of the solar

system, an electron with respect to the dimensions of the atom, or the homogeneous

spheres considered in Subsec. 1.1.6) and for which the motion of rotation is immaterial

admits as mathematical model a material point; the mechanical materialization of the

abstract concept of material point is called also

particle, denomination which we will

use pre-eminently above all in what follows.

Hence, a

particle (material point) is a geometric point to which we attach a finite

mass

> 0m

. The mass of this point is indivisible, as well as its support.

Frequently, a thread can be considered to be a

material line (a one-dimensional

continuous medium); a membrane will also be modelled by a

material surface (a two-

dimensional continuous medium). The material line and the material surface represent a

geometric line and a geometric surface, respectively, to which we attach a positive mass

that may depend on one variable or on two variables, respectively.

In general, a

continuous medium (a continuous material) will be a mathematical

model of a body, formed by a domain (one-, two- or three-dimensional) to which we

attach a positive mass (which can depend on one, two or three variables); all the

quantities in connection with such a medium will be represented by continuous

functions. The particle is a limit case of a continuous medium (the case in which the

Newtonian model of mechanics

domain is reduced to a geometric point). In a computation, it is customary to refer to a

point of a continuous medium, but this one is not a particle and has not a finite mass.

By a

mechanical system S we mean a set of bodies, modelled as continuous media

or as particles; hence, a mechanical system is formed, in the most general case, by a

finite number of continuous media and a finite number of particles. Usually, we will

consider

discrete mechanical systems of particles (formed by a finite number of

particles) or

continuous mechanical systems. The main mechanical results which are

obtained for a mechanical system have the same form either the system is discrete or

continuous; hence, the demonstrations which we will give, as well as the computations

we will make will refer to any mechanical systems. Various particular results will be put

in evidence if they have a certain importance. In general, a mechanical system is in

mechanical interaction with other mechanical systems; otherwise, we have to do with an

isolated mechanical system.

Let

Ω be the geometric support of a mechanical system S ; in case of a discrete

system of particles, this support will be formed by a finite number of geometric points,

while in the case of a continuous mechanical system this support will be a domain in

which the body is immersed. Taking into account the property of additivity (1.1.25) and

the definition of the integral, we may express the total mass (usually we will say only

mass) of the mechanical system in the form

dMm

Ω

∫

;

(1.1.70)

the integral is a Stieltjes integral and the mass

r()mm is a distribution.

Differentiating in the sense of the theory of distributions,

the unit mass (the mass of a

unite volume,

the density) is given by relation

ddmVμ ,

(1.1.71)

where the element of volume to which the corresponding mass is related can be an

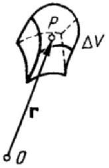
Figure 1.14. Element of volume.

element of line or of area; as well,

dm may be the three-, two- or one-dimensional

differential

considered in the previous subsection. In general (Fig.1.14)

(

)

(

)

= r;;Pt tμμ μ ,

(1.1.71')

where the variation in time of the density is also put in evidence. Returning to formula

(1.1.51), we may write