Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Problems of dynamics of the particle

461

h being a non-dimensional constant, while α is the amplitude. Representing 2()V θ

as a function of

(Fig.7.22), we see that the motion takes place only for

[]

1,1h ∈− ;

we may have also

1h > , but it does not correspond to a real angle α , the motion

being – in this case – circular. The condition

2()Vhθ

≤

allows to draw the curves

()ppθ= , symmetric with respect to the Oθ -axis, function of various values of h , in

the phase space. For

(1,1)h ∈− , e.g., for 0h

, the motion is oscillatory (we have a

simple pendulum). If

1h =

, then the motion is asymptotic, obtaining the lines of

separation (drawn with a thicker line) in the phase space; for

απ

it corresponds a

labile position of equilibrium. For

− it results a stable position of equilibrium (a

point in the phase space), corresponding

0α

. Noting that, for 0p > , q increases at

the same time as

t , we have indicated by an arrow the direction of the motion in the

phase space.

Figure 7.23. Topological structure of a phase trajectory depending on a parameter.

We notice that the separation lines are phase trajectories of the representative point

in the phase space; they do not allow to pass from a type of motion to another one. We

have seen that a singular point is specified by the equations

() 0

, 0p = , all the

other points being ordinary points; it results that an ordinary point is characterized by a

well defined direction of the tangent to the phase trajectory passing through this point.

We may thus state

Theorem 7.2.3 (Cauchy). Through each ordinary point of the phase plane passes a

phase trajectory and only one.

We notice that the equation (6.2.39') defines a field of vectors of components

,qp,

hence a field of velocities in the phase plane; hence, the singular point represents the

MECHANICAL SYSTEMS, CLASSICAL MODELS

462

point at which the velocity in the phase plane vanishes. The topological methods allow

to study the general topological properties of the phase trajectories defined by the

equation (6.2.39'). Taking into account the form of the phase trajectories in the

neighbourhood of the points of stable equilibrium (

− ), such a singular point is

called centre; analogous considerations lead to the denomination of saddle point for a

singular point of labile equilibrium (

Figure 7.24. Topological structure of the phase trajectory of a simple

pendulum in motion of rotation.

The topological structure of the phase trajectories may vary for some particular

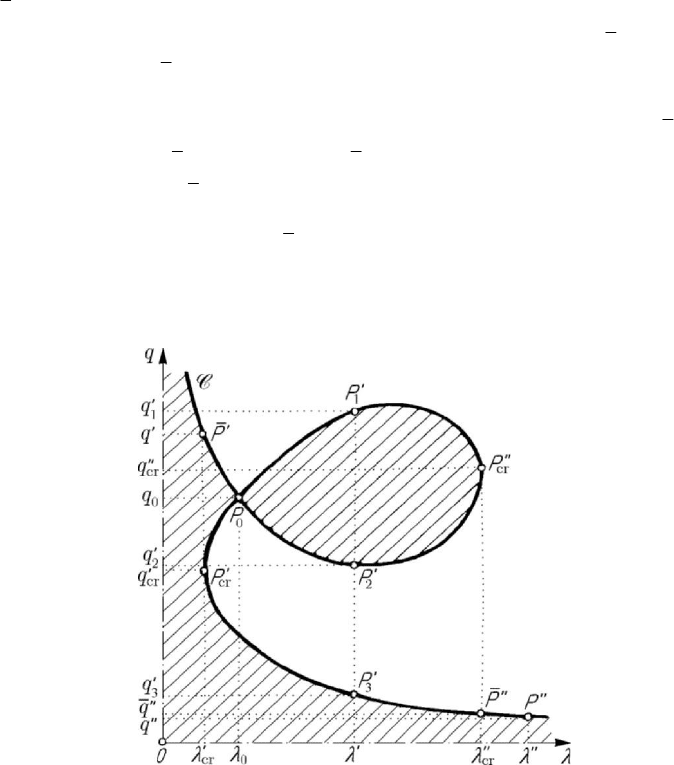
values of the parameter which appears in a first integral. After H. Poincaré, we

introduce the parameter in the differential equation in the form

(, ) (, )/

qVqqλλ=−∂ ∂ , the positions of equilibrium being situated along the curve

C of equation (, ) 0

q λ = (Fig.7.23). For various values of the parameter λ one

obtains three positions of equilibrium (for

λλ

′

there correspond the points

123

,,PPP

′′′

of ordinates

123

,,qqq

′′′

) or one position of equilibrium (for λλ

′′

there

corresponds the point

′′

of ordinate q

′

); one passes from three positions to only one

position by critical values of the parameter

λ (

cr cr

,λλλ

′

′′

), to which correspond the

points

cr cr

,PP

′

′′

, of ordinates

cr cr

,qq

′

′′

, and the points ,PP

′

′′

of ordinates ,qq

′′′

respectively. Noting that

d/d (,)/ (,)

qfqfq

λλλ

′

− , it follows that the critical

points correspond to the solutions of the equation

(, ) 0

q λ

′

(for which the tangent

to the curve

(, ) 0

q λ = is parallel to the axis

), assuming that (, ) 0

′

≠

. One

may thus state that the points of equilibrium appear and disappear two by two. We

suppose that the curve

C is a Jordan one, which divides the plane in two regions. We

notice that a straight line

λλ

′

pierces the curve C, for instance at the point

′

; if

(, ) 0

q λ

′

, hence if (, ) 0

Vqλ

′′

, below the curve C, then, for q increasing,

(,) 0

Vqλ

′′ ′

on C and (, ) 0

Vqλ

′

, over the curve C. It follows that

(,)Vq λ

′′

represents an isolated minimum of the potential energy, and the Lagrange-Dirichlet

theorem allows to state

Problems of dynamics of the particle

463

Theorem 7.2.4 (Poincaré). The positions of equilibrium of a particle which moves after

the law

(, )qfqλ

 in a conservative field are stable if the domain (, ) 0

q λ > is

under the curve

(, ) 0

q λ = , 0q > , 0λ > , and labile if this domain is over that one

(in Fig.7.23 the hatched domain corresponds to

(, ) 0

q λ > ).

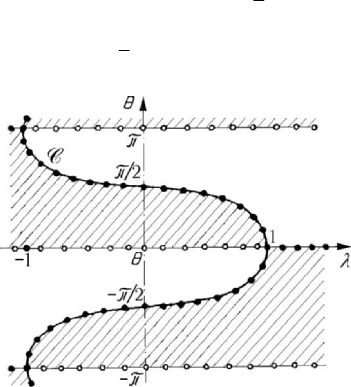
Let us apply these results to the case of the simple pendulum in a motion of rotation

(see Subsec. 2.2.2), governed by the equation (7.2.24') of the form

(, ) (cos )sin

θθλ θλθ==−



. The curves C are given by the straight lines 0θ =

and

θπ=± and by the curve arccosθλ

. Applying the Theorem 7.2.4, we find

stable branches of the curve

C (the points of equilibrium of centre type are denoted by

whole little circles, i.e.,

arccosθλ

and 0θ

, 1λ > , and θπ

± , 1λ <− ), as

well as labile branches (the points of equilibrium of saddle type are denoted by empty

little circles, i.e.,

0θ =

, 1λ > and

θπ

, 1λ

− (Fig.7.24). The points

0θ =

1λ = and θπ=± , 1λ =− are points of ramification of the equilibrium, while the

values

1λ

± are critical values (of bifurcation) of the parameter λ , corresponding

to those points. Taking into account (7.2.24'), it results that

0λ > , the domains of the

figure being thus restraint; as well, to have

1λ

the angular velocity ω must be

sufficiently great. If a separation line passes through the singular point

0θ =



, 0θ = ,

then the first integral (7.2.24'') becomes

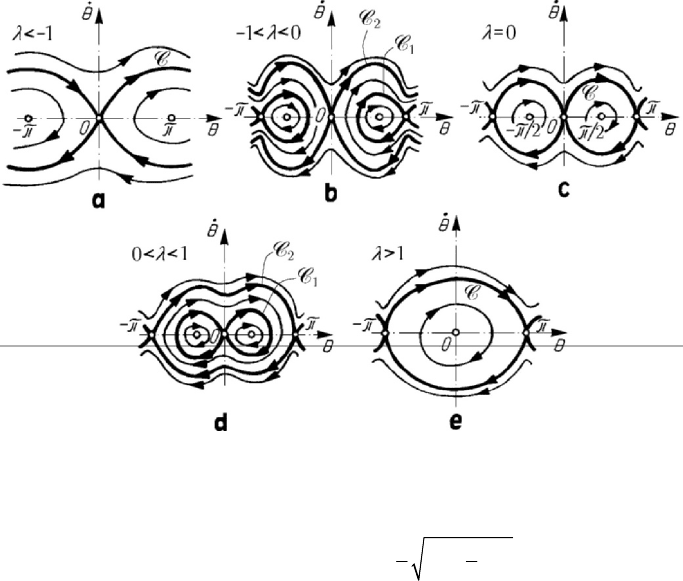
Figure 7.25. Phase space representation of the motion of a simple pendulum in rotation for

various values of the parameter λ : 1λ

− (a); 10λ

−

<< (b);

0λ

(c); 01λ

< (d); 1λ > (e).

sin 2 (1 cos )θθλθ=−−



2sin cos

θθ

θλ

±−



;

(7.2.30)

MECHANICAL SYSTEMS, CLASSICAL MODELS

464

if such a line passes through the singular points

0θ



, θπ

± , then the respective

first integral has the form

sin 2 (1 cos )θθλθ=++



2cos sin

θθ

θλ

±+



(7.2.30')

For 1λ <− , the singular points of saddle type 0θ



, θπ

± become singular points

of centre type (Fig.7.25,a), passing through

1λ

′

− ; for 10λ

−

<< appear two

separation lines

C and

C , the first of those ones surrounding two centres, while the

point

O becomes a singular point of saddle type (Fig.7.25,b). If 0λ = , hence if

ω →∞, then the curves

C and

C coincide with the curve C and form only one

line of separation; in this case, the centres are of abscissae

/2θπ

± (Fig.7.25,c). For

01λ<< one obtains two separation lines

C and

C , corresponding the equations

(7.2.30) and (7.2.30'), respectively, which pass through the singular points of saddle

type

0θ =



, 0θ = , and

0θ



, θπ

± , respectively; in the interior of the loops of

the curve

C there exist two other singular points of centre type, having the abscissae

2 arccosθλ=±

(Fig.7.25,d). If

1λλ

′

= , then the curve

C coincides with the

singular point

O , which becomes a point of centre type; for 1λ > remains only one

separation line

C (Fig.7.25,e). We observe thus that the separation lines correspond to

phase trajectories with different topological aspects.

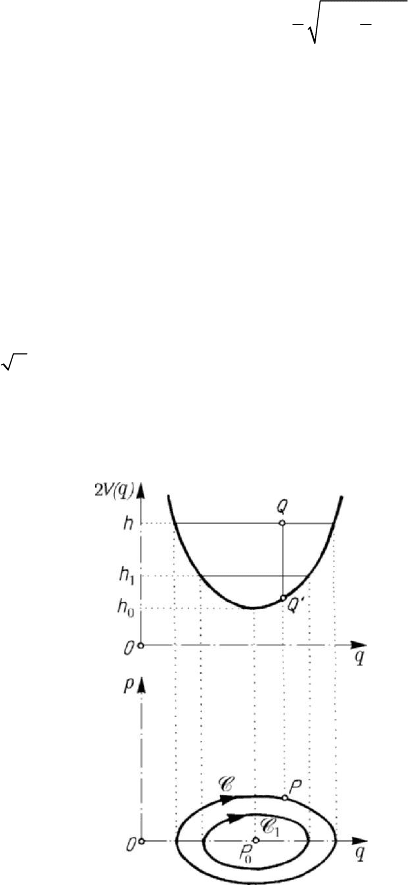
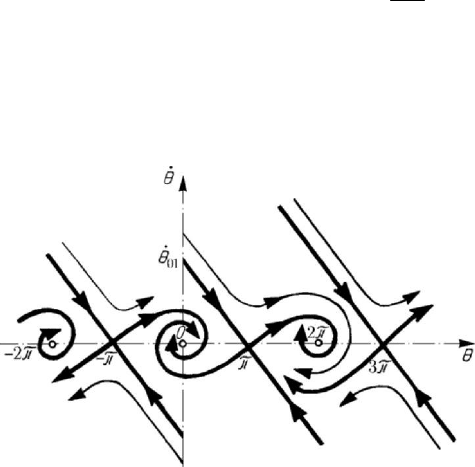
Figure 7.26. Potential function versus generalized co-ordinate diagram.

The above considerations allow to state, without demonstration,

Theorem 7.2.5 (Poincaré). The closed phase trajectories of a particle which is moving

after the law

(, )qfqλ= in a conservative field may surround only an odd number of

Problems of dynamics of the particle

465

singular points, the number of centres being greater than the number of singular points

of saddle type.

Sometimes, it is difficult to build up phase trajectories by analytical methods, so that

approximate methods, i.e., graphical or grapho-analytical methods are necessary. Thus,

we may give a graphic representation of

2()Vq as function of q (Fig.7.26); drawing a

parallel of applicate

h to Oq , we may measure the difference 2()QQ V q h

′

− . By

the formula (6.2.40), the radical of this difference allows to specify the representative

point

in the phase plane, setting up the phase trajectory C by points. Starting from

hh= , we obtain the curve

C a.s.o.; to

corresponds the singular point of

centre type

P .

Figure 7.27. Phase space representation of the motion of a simple

pendulum in a resistent medium.

In the case of a dissipative mechanical system with a single degree of freedom, of

equation

() ( )qfq Fp=+ , () 0pF p

≤

, we start from the considerations made in

Chap. 6, Subsec. 2.2.5. Multiplying this equation, which corresponds to linear or non-

linear damped free oscillations, by

dq and integrating along a closed phase trajectory,

it results

d()d()d0pp fq q Fp q

∫∫ ∫

 

;

noting that

()d 0fq q=

∫



too, we get

()d ()d 0

Fp q Fppt

∫∫



where we have integrated on a time interval equal to a period

T . Because the product

()pF p maintains a constant sign, it results that we cannot have such a relation, and the

motion cannot be periodical.

MECHANICAL SYSTEMS, CLASSICAL MODELS

466

We have seen in Subsec. 1.3.3 that, in the case of the motion of the simple pendulum

in a resistent medium, the angular velocity is given by (7.1.53''); the condition

0θθ=



≷ for 0θ = leads to

()

22 2 2

ecos2sin

41 41

ωω

θθ θ θ

⎛⎞

=− +

⎜⎟

⎝⎠

∓



∓

(7.2.31)

where the signs

± correspond to

0θ



≷ , respectively. The points 0θ =



, nθπ= ,

n ∈  , correspond to positions of equilibrium; the equilibrium is stable for n even

(the corresponding singular points are of focus type), while for

n odd the equilibrium

is labile (there correspond singular points of saddle type (Fig. 7.27)). If

()



, n odd,

(7.2.32)

then we notice that for

θθ<



the particle oscillates, the motion being damped

around the stable position of equilibrium

0θ



, 0θ

; if

θθ=



, then one obtains

the asymptotic motion of a particle. For

01 03

θθθ<<



the particle effects a complete

rotation and then its oscillatory motion is damped; in general, if

0, 2

θθθ



, n

odd, then the particle effects (1)/2n

complete rotations, passing then in a regime of

damped oscillations around a stable position of equilibrium.

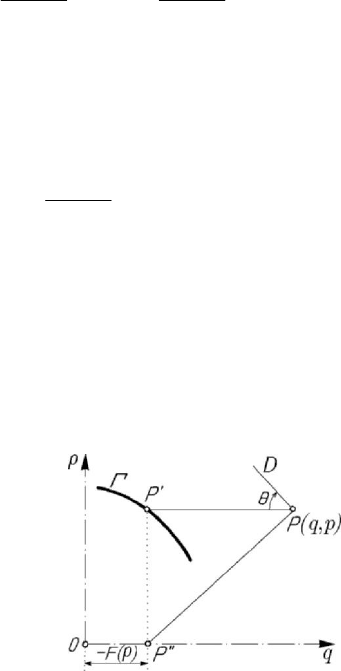
Figure 7.28. Application of Liénard’s method in a phase space representation.

As in the case of conservative systems, in the case of non-conservative (dissipative)

systems we may use approximate methods of phase trajectories in the phase plane. For

example, in the case in which

()

one may use Liénard’s method. Thus, one

draws first the curve

Γ of equation ()qFp

− (Fig.7.28); starting from the

representative point

(, )Pqp , one draws PP

′

, P Γ

′

∈

, parallel to Oq , and then

′′′

, parallel to Op , POq

′′

∈

. A perpendicular D at P to PP

′

is inclined with

respect to

Oq by the angle θ given by

[

]

tan ( ) /qFp pθ

+ ; taking into account

(6.2.43), it results that the straight line

D defines the slope of the phase trajectory at

Problems of dynamics of the particle

467

P . Step by step, starting from an initial position, we obtain a polygonal line which

approximates the searched phase trajectory. We mention also other approximate

methods of computation, e.g., Drobov’s method, Pell’s method, the “delta” method etc.

In the above conditions, we have supposed that

() 0pF p

≤

, hence that this product

has a constant sign. But if this product is positive for small values of

, then the state

of equilibrium is not yet known, a motion being developed starting from this state; if the

product becomes then negative, the damping force being opposite to the velocity for

great values of

p , then the amplitude begins to be damped. The respective motion is

automaintained and will be considered in Chap. 8, Subsecs 2.1.4 and 2.2.7.

Chapter 8

DYNAMICS OF THE PARTICLE IN A FIELD OF

ELASTIC FORCES

In the problems studied till now, we considered – especially – the action of a

gravitational field (a field of parallel forces, the supports of which pass through a fixed

point situated in a plane at infinity) on the motion of a particle. We consider now the

case in which the particle is acted upon by central forces (the supports of which pass

through a fixed point at a finite distance). First of all, the general case of arbitrary

central forces is presented, then the cases in which – after Bertrand’s theorem – the

orbit is a closed curve (the case of elastic forces and the case of forces of Newtonian

attraction are considered). In this chapter we study, in detail, the motion of a particle in

a field of elastic forces.

1. The motion of a particle acted upon by a central force

In what follows, we firstly give some general results concerning the equations of

motion of the particle subjected to the action of a central force; we make also a

qualitative study of the trajectory. Then it is shown that the problem of two particles

leads to such a case of motion.

1.1 General results

The study of the motion of a particle subjected to the action of a central force leads

to Binet’s equation and formula, for which one obtains interesting qualitative results;

Bertrand’s theorem puts in evidence the two cases in which the trajectory is a closed

curve.

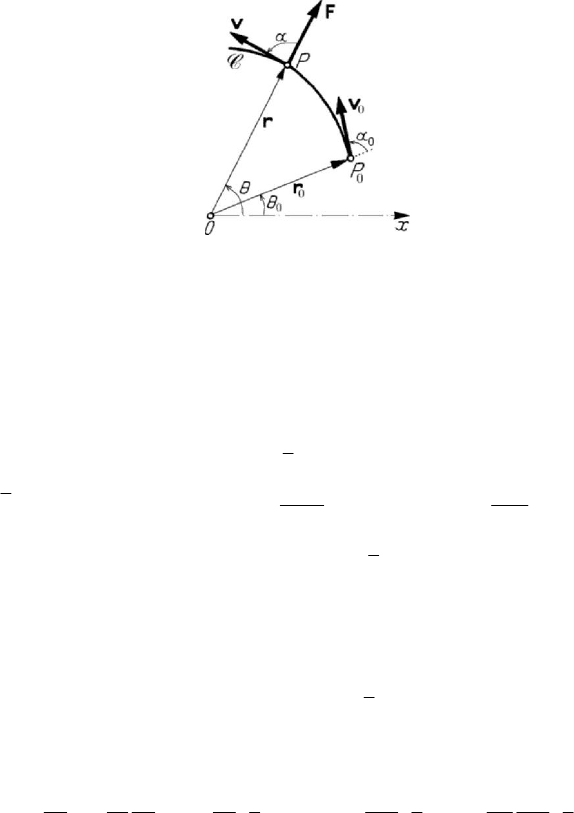
1.1.1 Central forces. Binet’s equation

Let us consider a particle

acted upon by a central force

; the equation of motion

is of the form



r .

(8.1.1)

As it was shown in Chap. 6, Subsec. 1.2.6, in this case the trajectory is a plane curve

taking the plane of the curve as

Ox x -plane and using the results in Chap. 5, Subsec.

1.2.4, we may write the equations of motion in polar co-ordinates in the form

469

MECHANICAL SYSTEMS, CLASSICAL MODELS

470

(

)

mr r Fθ−=



 ,

(

)

20mr rθθ



 .

(8.1.1')

The second equation leads to the first integral (corresponding to the formula

(6.1.59))

2 rrvC

θ===



00 0 00 0

sin constC r rv rv

θα=== =



(8.1.2)

Figure 8.1. Particle acted upon by a central force.

where

Ω is the areal velocity of the particle P , the constant C being specified by the

initial conditions (Fig.8.1)

()rrt= ,

()tθθ= ,

()vvt

()tθθ=



000

(, )α

 rv .

(8.1.1'')

Taking into account (8.1.2), the first equation (8.1.1') may be written in the form

mr F



()() ()

,,,; ,,,; ,,,;

Fr r t Fr r t Fr r t

θθ θθ θθ=+=+

 

(8.1.3)

too, where we have introduced the apparent force

(we notice that the supplementary

force

/mv r

is of the nature of a centrifugal force); the system of differential

equations (8.1.2), (8.1.3) determines the functions

()rrt

, ()tθθ

, the three

integration constants which appear being specified by initial conditions. If

(,;)FFrrt=  , then the motion along the radius vector is given by the unidimensional

equation of Newton, where the apparent force

F is used, the angle θ being then

obtained from the integral of areas.

Successively, we have

(

)

ddd1

ddd

rCr

θθθ

== =−



 ,

(

)

(

)

222

d1 d1

θθ

=− =−





and, replacing in the equation (8.1.3), we obtain Binet’s equation (we suppose that

/0FFt≡∂ ∂ =



)

Dynamics of the particle in a field of elastic forces

471

(

)

d1 1

mCθ

+=−

(

)

,,,FFrrθθ=



 ;

(8.1.4)

analogously, by eliminating

r and θ



from the expression of the force F , we get a

differential equation of second order, which determines the trajectory of the motion in

the form

(; , )

θ= .

(8.1.4')

The initial conditions

(; , )fCC

θ =

cot

(; , )

fCC

′

=− =−



(8.1.4'')

where we have put

00 0

cosrv α=

and /

f θ

′

≡

∂∂, allow to determine the integration

constants

and

. The integral of areas specifies the motion on the trajectory in the

form

(; , )

∫

(8.1.5)

Noting that

d(/)d[(/)]dFr rr Fr⋅= ⋅ =Fr r r , the theorem of kinetic energy

leads to

(,,,;)d

Ftρθρθ ρ−=

∫



If (, )FFrθ=



, hence if ()FFr

, then we may write a first integral of energy,

hence a first integral of Binet’s equation in the form

(

)

d1 1 1 2

()d

ρρ

⎡⎤

⎡

⎤

+= +

⎢⎥

⎢

⎥

⎣

⎦

⎣⎦

∫

(8.1.6)

noting that

22222 22

/vrr rCrθ=+ =+





; we may obtain this result multiplying both

members of Binet’s equation by

d(1 / )/dr θ and integrating. The given force is, in

this case, conservative and we may introduce the simple potential

()UUr= , so that

() () d /dFr U r U r

′

== . The first integral (8.1.6) becomes

(

)

(

)

22 2

d1 d

()

22d d

mr mC mC r

Ur h

θθ

⎡⎤

===+

⎢⎥

⎣⎦



() ()

Ur Ur

=−

()

hUr=−

(8.1.6')