Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. т а ін. Вища математика у прикладах та задачах. Ч 3
Подождите немного. Документ загружается.


Глава 2
581
2.248. /(*)=-
2.249. Дх) = X
X
(-о-т
1
-
Л
„=Г„ І-'л
1-(-1)
я
1-іл
,2 +«
V"-2-250. /М =
^-
+
2Х^»
2л 1+/7- З ~ л
2
2.251.
Дх) = У ІІІІе"" .
2.252. Дх) = -?- £ —
2л
„
=
.„и
2.253. /(х)= X
<ЯЙ
- І
зп
(1
+ /ли) - — зп (/ли) |<?"
1,1 +я. V пп
2.254. Дх):
•+
X (-')"
ІЛІМ
2 + тп ~г-
2 „гТ^
4
' 4 + л
2
я
2
їда
2.255. Дх) = - + — X
4 2л ^
1 1 і: є
2
-1
г
,
ч
2
Г
зіп а 4
+
Г .
2
сх
зіп
ах ,
2.256. Дх) =
—
— созсххага. 2.257. Дх) =
—
зіп аа;
71
о
а
Ї^-Л
= -. 2.258. /(
Х
) = 4= Се~
4
созахасх.
о '
4
,,
ч
2
+
Гзіпал . 2
+
Г ал созах ,
2.259. Дх) = — -зіп ах сіа . 2.260. Дх) = — соз -сіа.
л о !-«
71
о
2
!-«
2.261.
/(х) = -І
+
Г
—в""^.
2.262. /(*) = - [
2 7 є""
я * а
2.263. Дх) = -і- |
аЄ
сіа. 2.264. Пх) = ~ ( е
її
;
/1-і.
/м^ V 7тт 7
л _„ 4 + а'
с/а.
я_-(1 + а
2
)
3
2л
І-/а
І
+ а
2
аа.
2.265. (а) = Ж
—Ц-,
/г, (а) = Ж -5Ц-.
їл
і
+
а
2
Піт
І
+ а
2
. а а
пг зіп а -зіп— пг соз
2.266. /у (а) =. 2., /л-(а) -
л
2
—
їла
V
л а
соз а

582
Відповіді
ііап
і? /2
1
+
созал
12
зіпа;
2.267. /у (а) = — —, (а) = Л-
»я 1-а
2
«л 1-а
т>£« с /2 зіпаа , /2 1-со:
2.268. Р
с
(а) = ^ , /\у(а) = .
Ї7і
а їл а
-
соз
аа.
1 4 —
2.269. Р(а) = ~==? соз га. 2.270. р(а) = е
2
72л
1-4а
2
2.271.
Р(а) =
/
Д " . 2.272. Я"(а) = Д
2
V
л: (а
2
+ 1)
2
V те
а
2
+А
2
А
2
2.273.
/їа) = -
21
ае
-
5Іпа
-«
с
^
а
Тіл
е(1 + а
2
)
Гл а в а З
3.1.а)7 + 3/, 22 + 7/; б) 272, 5. 3.2. а)-0,4 + 2/, 0,12 + 0,24/; б)-/,
--—/.3.3.
а)0; б) -— ; в) 3.3.4. а) 0; б) -2/;в)0; г) - — +—/.
6 6 17 25 50
3.5.
а) 6+Пі; б) -4/; в) -29 + 22/. 3.6. а) ~- — і;б) і; в) —і;
17 17 5
13 13 25 9 20
г)
-
+|і. 3.7. а) + б) ~(4 + 3/). 3.8. а)* = 1, у = -2 ; б) х
=
Щ,
,
=
-!£;„),Л,
у
= і;г)х = —
г
^
г
, у = —^.3.9. (4,3),
17 3 4 а
г
+Ь
2
а
2
+Ь
2
(5,
3), (4, 4), (5, 4). 3.10. а) (-2, -2), (2, -2); б) (-1, -4), (1, -4).
3.11.
а) -4/, 1 + /—;б) 10-2/, -—-—/. 3.14. а) -1-і; 6)0, -1,
2
2 4 4
і 7з
-± — /.3.15. 2, =1-/, 2
2
=/.3.16. а) 1, £; б) 1, -і; в) 5, я;
12
2 6
г) 72,
-
т
;д)7, -~;е)2,
-^;є)1,^;ж)
774,
-агсіД;
4 3 3 4 5
Ті 6
з) ТУ,
-агсі8~;і)
7Ї0,
-агсі£3;к)
1, --у .3.17. а) |г| = 3,
Аг§2
= л + 2А7Х, хє2;б) |г| = 1, Агег = ~ + 2*л,
А
є 2; в)
) 21
= 1,

Глава З
583
я Зя Зя
Агег = — + 2кк, к є 2 . 3.18. а) соз —+ /зіп—; б) 2(соз я + /зіпя);
2 2 2
в) 2
5я . 5яА . .( Зя . . Зп\
ч
6я . . 6л
соз — + /зіп— ; г) 2 соз і-'зіп— ; д) соз
г-'Зіп—
З 3 4 4 7 7
е) соз- +/зіп-. 3.19. а) -1728; б) 2
9
(1 -/л/з ) ; в) -2
,9
(1
-/л/з)
; г) 0.
6 6
1 л/з 1 л/з
3.20. а) 1,-1; б) 1, —+ /—, 1— ; в) 1, /, -1, -/.
2 2 2 2
3.21.
а) ±-Ці + /);б) -(+л/з+/),-/; в) + (соз/зіп- |,
\2 2 ^ 8 8)
,( Зя . . Зя
А
ч
(п 2к ,Л . . (я 2я, , ,
п
.
±1 соз—+/зіп— |; г) соз | — + —я
І+/5Ш
—+ —« |, я = 0, 8 ;
6 9
к =0,1,2 ;
д)
+
^
(1 +
/Л
/І);
е)^(соз^+^я
^/зіп^З* |
є) '^соз + у * ]+ + ^
А
11,
А
= 074 . 3.22. а) ^ + /^.
——'-уг;
6
)
2, 2/,-2,-2/; в) ±1, ±/,
^у-(+1+
/). 3.23. а) 2е
т
;
2л з , с 12 \
ІШСІВ
Т
'агс»вІ-у І
л
- /
—
/— — і— / і і
шілц
—
б) \е
2
; в) 1-е
2
;г)2е
3
; д) л/34 е
5
; е) е
Нагсів— +іг| _ /|л-агсІ8—І /|о+—)
є) 5е (
3
^;ж)л/5е^
2
^;з)1-*Л
2
^. 3.24. а) 24е
2
,у;
б) 16е
4
, 2е
2
.3.25.
а) Коло радіуса /? з центром у точці
2
0
;
зовніш-
ність круга, обмеженого цим колом; внутрішність того самого круга;
б) при 2а >
12,
-
2
2
1
- еліпс з фокусами в точках 2, і г
2
, велика піввісь
якого дорівнює а; при 2а - -
2
2
1
- відрізок, що сполучає точки 2, і
2
2
;
при 2а <
12,
-
2
2
1
- пуста множина; в) гіпербола з фокусами в точках
2,
і
2
2
,
дійсна вісь якої дорівнює а. 3.26. а) Вся комплексна площина, з
якої вирізано круг радіуса 2 з центром у початку координат; б) круг радіу-
са 1 з центром у початку координат з виколотою точкою 2 = 0.
3.27. а) Коло радіуса г = 8 з центром у точці 2 = 5/; б) круг разом з межею
радіуса г = 4 з центром у точці 2 =
1
+ /. 3.28. а) Сектор, обмежений про-
я
менями /,:
аг§2
= 0, /
2
:
аг§2
= — (промінь /, не належить сектору);

584
Відповіді
б) частина кільця, обмеженого променями аг§2 = та аг§2 = і колами
радіусів г = 1, г = 2 з центром у точці г = - /. 3.29. а) Півплощина, що
розташована нижче прямої у = 1, включаючи цю пряму; б) круг радіуса 1
з центром у точці 2 = 0, включаючи коло; в) внутрішня частина круга ра-
діуса 2 з центром у точці г = -і, виключаючи його центр і саме коло.
3.30. а) Зовнішність кола радіуса 1 з центром у точці (1, 0); б) півплощи-
на, що знаходиться зліва від уявної осі; в) частина площини зовні парабо-
ли у
2
=
1
- 2х , якій належить точка 2 =
1
. 3.31. а) Коло радіуса 1 з
центром в точці 2 = 0 з виколотою точкою 2 =
-1;
б) коло радіуса а з
центром в точці 2 = 0 з виколотою точкою 2 = - а ; в) парабола у
2
= 2х +
1
.
3.32.
а) Гіпербола ху = 1; б) гіпербола х
2
-у
2
= 1; в) коло х
2
+(у +1)
2
= 1.
2 2 1 2 ( П
2
9
3.33.
Гіпербола х -у = —. 3.34. Коло (х+ 1) "4-У
-
"2)
3.35. а) Коло х" + у = 1; б) пряма, перпендикулярна до відрізка 2,2
2
, яка
проходить через його середину; в) гіпербола ^х -11 - у
2
= 1; г) парабо-
ла у
2
= 2х +1. 3.36. а) 2-2=0 та 2 + г=0;б) 2 + 2 +/(2-2) = 0;
в)
А
(2+ 2)+ 26+ /(2-2) = 0.3.37. а) 2
2
+і"
2
= 2а
2
;б) 2-2"+
г
+ 2=0.
3.38. а)
Кем>
= х + 2ху, \тч> =
у
2
-х
2
- у; б)
Кеи^х
2
-}/
2
,
Іти' =
1
+2ху;
2 _ 2 2 ,
в)Яеи> = Зху
2
-х
3
, Іти' =
1-Зх
2
з'
+ у
3
;г)Кеи' = ^--—
У
—, \тлу = —
Ху
.
х +у х +у
3.39. а)
м>
= 2
2
+ 2/2
—
1; б)
м>
= 2 +1; в) УУ = _
2
4
'
2
. 3.40. а)
ч>
=
-1;
сч т л- ч
1
+ ' ч 5 + 12/'
2
у
о)м> = -3-4 /; в) >с = ; г) и> = . 3.41. а) Коло и + V = 4, що
2 13
проходиться за годинниковою стрілкою; б) вісь ОУ (виключаючи точку
О),
що проходить так: спочатку від 0 до +°°, потім від -оо до 0; в) про-
мінь,
що йде по бісектрисі третього координатного кута з -оо до 0.
3.42.
а) Парабола V
2
= 4С
2
(С
2
- и); б) коло |
и>
| = /?
2
, що проходиться
двічі; в) промінь аг§ м/ = 2а . 3.43. а) Неп" = е~
х
соьу, \т\у = -е~
х
%'ту;
2_
2 2_ 2
б) Кеи> = е*
у
соз2ху, 1іт^ = -е
дг у
зіп2х_у ; в) Кеи> = зіпхсЬу,

Глава
З
585
Іпти'
=
созл-зНу
; г)
Кеи»
=
спхсоз(у-1),
Іти
1
=
&Ьх$'т(у-1);
д) Кем>
=
спхсозу
, Іти' =
сЬхзіпу
. 3.44. а) | м'| = 1,
аг§и>
= —^;
б)
|м;| = і,
аг§и'
= ^. 3.45. а) |^| =
сЬ1
,
ащц>
= ~; б)
|и>|
=
со8
2
(1пЗ),
аг§н>
= 0 . 3.46. а)
|
м>
| =
тс, аг§>у
= —^ ; б) |
ч>
| = тс
2
,
аг§\у
= 0.
3.47.
а)
сп1соз1-/зп1зіп1;
б)
/зпл;в) сЬл.3.48.
а)соз1;
б) -5п2со5І
+
/сп2зіп1;
в) /. 3.49. а)(2А
+1)
пі,
Ає2;б)
у;
в) ^2А+-^л/,
А
є 2. 3.50. а)
/ш|;б) -/сіпл;
в) 0.
3.51.
а)
Агсзіп/==2Ал-/1п(л/2-1), Агсзіп
/ = (2к +
1)л-/Іп(л/2
+1), ке 2;
б) Агссоз
/ = Ал + -^ 1п2, Ає 2;
в)АгсІ§^
= ^2А+^л-/Іп(72 + 1),
Агсі§^
=
^2А-^л-/Іп(л/2-1), Ає2.3.52.
а) е
{
2к+2
У,
Ає2;
б)
І
2
*
+ 2
К
Ає2;в)
є
-2
*",
Ає2;г) е^+і)*^
Ає
2.3.53.
а)
е
~Т
(,+8
*
,
і
4< + - к
(;-1)І2/.+-к
Ає2;б)<Л
2
^,*є2;в)е'
6
> , Ає 2. 3.54. г
к
=( 2А--^ |л/ ,
Ає2.3.55.
2* =
(2А
+
і)л±/Іп2, Ає2.3.56.
2
4
=
^А-^л/,
А
є 2.
3.57.
х =
0.3.58.
г
2к
= 2Ал/ ,г
2к+]
=
(2А
+ 1)л/+
ІпЗ,
А
є 2. 3.59. а)г = 1-/;
б)
2 =-е + /.
3.61. -6.3.62.
1
+
/.3.63.
-л.3.64.
1.3.65.
-2/. 3.66. -.
9
3.67.
о°.3.68.
~>.
3.69.0. 3.71. а)1±і;
б) ±2/; в) /, 3-/. 3.72. а)
Ніде
не
диференційовна;
б) у
точці
г = 0; в) у
точці
2 = 0; г)
ніде
не
диференційов-
на. 3.74.
а) Ні; б)
так;
в) ні; г)
так;
д) ні; е) ні; є) так.
3.75.
Д2) =
2
3
+2 +/.3.76.
/(2) =
1(2-/)
2
2
. 3.77. /(2) = (2
+/)г
3
.
3.78.
/(*) = -. 3.79. Д2) =
2зп2-2
2
.3.80.
Дг) =
4сЬ2
+
2
2
-1.
2

586
Відповіді
3.81.
Д« = 0,
у(х,у)
=
3х
2
у-у
3
+С, /(г) = 'х + іу)
3
+ С/ = г
3
+ С/.
3.82.
АУ = 0,
и(х,у)
= 2е
х
сову
+
С, /(г)
^2е
х
(сову
+
івту)
+ С = 2е
:
+
С.
3.83.
Аи = 0,
у{х,у)
= -х
2
+у
2
+ С,
/(г)
=
-/(х
2
-у
2
+
2/ху)
+
3
+ С/ = -/2
2
+
3
+ С/.
3.84.
Дм = 0,
у(х,у)=
~
У
+ 2х + С, /(г)= ^""'^ -2у +
2іхч-Сі
= - + 2іг + Сі.
X
+у X +У 2
3.85.
Ди^О,
у(х,у)
= -1(х
2
-у
2
) +
2х>>
+ С,
Дг)
= г
2
-і-2
2
+ С7 =
~2
2
+С/.3.86.
Ду = 0,
и(х,у)=^(х
2
-у
2
) +
С ,
/(г) = -г
2
+ С
.3.88.
а) Ні; б) так; в) ні. 3.89. а) /-, = 2, ф, = -; =Д,
2
4 " е
Ф
2
= ™ ; б) г, = 1, ф, = 0 ; г
2
=
л/сп
2
1
—
кіп
2
1,
ф
2
=
-агсІ§(г§1
•
ІЬ1);
4
в)
/-, = 15, ф, =
-агсі§
- ; г
2
= і
(
~2
я
) , 4я
1
+ , ф
2
=
я-агсі:
ч
4[" " я
2
-4
3.90. -1.3.91.
- —+
9/.3.92.
1
+
/.3.93.
~{е
2
-
1)(1
+ /).
3.94.
0. 3.95. 0.
З
4 ^
3.96.
а) 2 + /; б) 6 + 2 /.
3.97.
2я /.
3.98.
-2
(1
+
/). 3.99.
-1.
3.100.
а) | (/ -1);
б) 7 +
19/.
3.101.
С05І-8ІПІ-/Є
4
.
3.102.
1
-созі + г(зіп
1
—1).
1
я
4
3.103.
-(1-008(2+
2/)).
3.104. 2(/-1). 3.105.
—.
4
64
3.106.
-1
8
^
+
31п
2
2
+ /-1п2. 3.107.
-—.
3.108. 0.3.109.
пі.
8
8
3.110.
ї^-/.
3.111. /язпя
.
3.112.
0.
3.113. /-яспя. 3.114.
0.
3.115.-—.
2
3 45
3.116.
0.
3.117.-Я/.
3.118.
я/.
З.П9.-^-
Л
+
2)л
^;.
3.120.
0.
3.121.-—
.
8
127
2
, Г
3.122.
-—зН
1.3.123. ——-/.3.124.
-2я/.
3.125. Розбігається.
2
32

Глава
З
587
3.126. Збігається. 3.127. Збігається. 3.128. Збігається. 3.129. Розбігається.
3.130. Розбігається. 3.131.
/? =
1.3.132.
К =
1.3.133.
/? =
л/2.
3.134.
/? =
+«>. 3.135.
/? =
1.3.136.
Л =
1.3.137.
Л =
1.3.138.
Л =
+°°.
3.139.
-- + 4-2
з
з
2
2
у
2
3
+...,
Я =
1.3.140.
£
я = 0
Г-П"
+1
2"
З
3"
+|
2
2
2
3.141.
-зіп1
+
2(2+1)со5І+у(г
+
1)
2
5Іп1-у-(2
+
1)
3
соз1-...,
Л =
+°°.
3.142.
л/е
1+І(2
г
-1) + -Ц-(2г-1)
2
+-Ц-(2г-1)
3
+...
2
2!2
2
3!2
3
143.
--У —
(2
+
2)"
, /? =
-.3.144.
1
+ -У - , /?
5~
0
5
я
3 2
„^,(2,1)!
= +°о.
1
~ т
2
" 1 ( Т
2 3
^
3.145.
-У ——, К = +°°.
3.146.
1п2— - + — + —
+...
2„-Го(2я)! 2^2 2-4 3-8
3.147.
-—+
—
1
-г2
3
+-^-г2
5
+..., Л = п.
2
2
2
3!2
3
512"
1
Г
2
3
+...,
Я =
л/іп
2
5
+ л
2
3.148.
- + —
2
-гЧ
6
б
2
2!6
3
3!6
3.149. 1п2--!-2
+ —Ц-2
2
-—
]
—г
4
+..., Я = л.
, /?
= 2.
3.150.
-ї-2
2
+і-2
4
+і
4
-2
6
+...,Л=".
2!
4! 6! 2
-
2
-
4
11
3.151.
1п2-—+-Ц-+
Г
:
6
+...,
Л = л.
3.152.
І2
+
/|>е.
4
3-2
4
90-2
6
3.153.
\г\>~.ЗЛ54.
| > 2 .
3.155.
121
>
е'
{
.
3.156. |г|>е.
л/2
3.157. І2
+
і|>-.3.158.|2-2-/|>-. 3.159.12
+
2/|>3. 3.160.1
г + 1-/І> 1.
4
1 1
2
11 11
3.161.
-і +
2
2
+—!— !—
+
....3.162.
—
£(2-1)"
;
2 4І2
2
6І2
4
2-1 ^
и = 0
+
У(-1)"(2-2)"
-
3.163.
а)і+ У —; + \ + — + - +
-+...;
2-2
л=0
2
„
=0
Л!
2- 2'
2І2
3! 4!
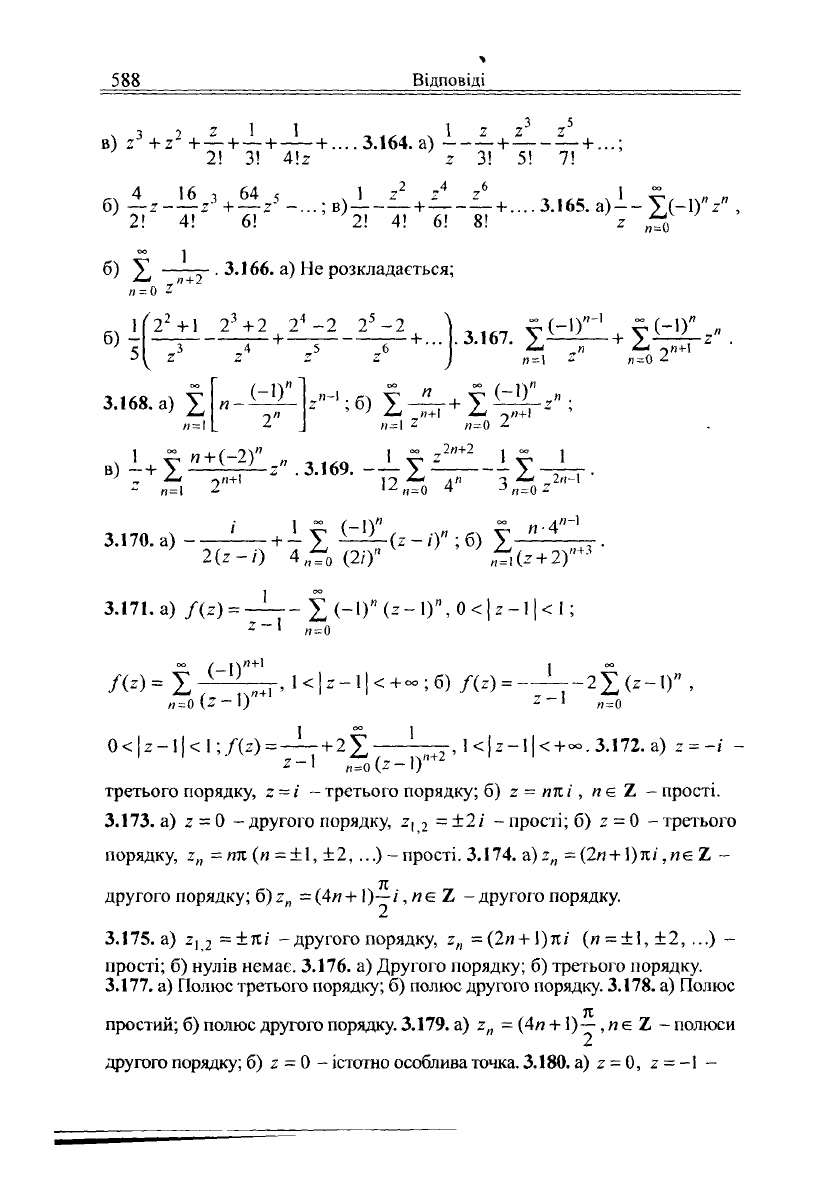
588
Відповіді
ч 3 "> 2 1 1 , .,
л
. 1 2 2
3
2
5
в) 2 +2" + —+ —+ + .... 3.164. а) + +...;
2!
З! 4І2 2 3! 5! 7!
4
16 з 64
5
.1 2
2
2
4
2
6
, .1 V, ,ч» н
б) —2 2 +—2 в) + + .... 3.165. а)-- > (-1) г ,
2!
4! 6! 2! 4! 6! 8! г ^
л=0
1
б) ^ —^-^ . 3.166. а) Не розкладається
1
л = 0 2
/і2
б)
3.168. а) £
Л
=
І
2"+1 2
3
+2 2
4
-2 2
5
-2 ^
З
.,б7.
хНП^НЇІ,..
^-1 Л -)Л+1
л=1 -і я=0 2.
(-1)"
2"
.1-1
(-О" л .
і—І
я + 1 ^ ТЛ+1
п=1 2 „
=
о ^
, оо _2л+2
- л=1 2 '^п=0 4 ^=0^
4
л-1
3.170. а)
+
і £ - і)" ; б) £ , .
2(2-/) 4„То (2/Г ^,(2 + 2Г
3
3.171.
а) /(2) = -- £ (-1)" (2 - 1)\ 0 < 12
-11
< І;
2-1
л = 0
(-1)"
„То (2-1)
л+1
1<І2-1І<+~;б) /(*)
=
-21(2-1)",
я=0
0<
Іг-11
< 1; /(г) = —1_ + 2У, !—-,
1<І2-1І
<+<*>. 3.172. а) 2 =-і -
г 1
я=о(2-І)
третього порядку, 2 =
1
-третього порядку; б) 2 = пкі, пе 2 - прості.
3.173.
а) 2=0 - другого порядку, г
( 2
= ±2/ - прості; б) 2=0 - третього
порядку, г„ = яті (и = + 1, ±2,...) - прості. 3.174. а)г„ =
(2/7
+ 1)я/ , иє 2 -
к
другого порядку; б) г
п
=
(4/7
+1)—/', и є X - другого порядку.
3.175. а) 2,
2
=±ти - другого порядку, 2
Я
= (2и + 1)тг/ (и = ±1,±2, ...) -
прості; б) нулів немає. 3.176. а) Другого порядку; б) третього порядку.
3.177. а) Полюс третього порядку; б) полюс другого порядку. 3.178. а) Полюс
ті
простий; б) полюс другого порядку. 3.179. а) 2„ = (4и +1)—, и є 2 - полюси
другого порядку; б) 2 = 0 - істотно особлива точка. 3.180. а) г - 0, 2 = -1 -

Глава З
589
полюси другого порядку; б) г = 0 - полюс другого порядку,
г
п
=2ппі (я = ±1, ±2,...) -прості полюси. 3.181. а) 2 = 0 -усувна особ-
лива точка; б) 2 =
1
- істотно особлива точка. 3.182. Полюс простий.
3.183.
Полюс простий. 3.184. Усувна особлива точка. 3.185. 2 = 0- полюс
четвертого порядку; : =
—
1
- полюс простий. 3.186. Усувна особлива точ-
17 е
2
ка. 3.187. Істотно особлива точка. 3.188. гез/"(-1) = , гез /Ї2) = —.
54е 27
3.189. гез/(0) = 0,
гезД
^
л
=
—,
гез Д
—Ь
ТС/7
= -
п \2 ) л(2я + 1)(4я + 1)
3.190. гезД-1)= —, гез/(2) = ——. 3.191. гез ДО) = -1.
27 27 6
3.192.
гезД0) = 0.3.193. гез/(-/) = Ізп2• /, гез/^= ~{е + 2е'
х
)і.
3.194. гезД0) = -1, гезДЗ) = — зіп
2
-.3.195. гез/(-3) = -—,
6 27 2 8
ге8/(-1)
=
4,
гез Д1) = 4-3.196. гезД0) = -4р
гез/Г-^О.
о
б л [ 2
3.197. гез ДО = -1.3.198. гез {(пп) = 0 , я є 2. 3.199. -4л/. 3.200. -.
е
3.201.0.3.202. 2(1-е
_|
)к/.3.203. -—.3.204. - —ІпЗ. 3.205. 2л/.
З З
3.206. пі. 3.207. 0. 3.208. 2л/ —. 3.209. 0. 3.210. 2л/.
З
зіп1-4соз1 . , „ , „., „ . 2паЬ
3.211.
пі. 3.212. 0. 3.213. Зл/. 3.214.
12
(а
2
-Ь
2
)"
2
'
3.215. ,
2
* .3.216.0. 3.217. ,
2
" .3.218. -=====.3.219. пі
Р
2
(р
2
-\)
уЦІ]
3.220. . 3.221. 2л . 3.222. -л . 3.223.
Л
аЬ{а + Ь) ' (пі)
2
' 3 . (2т + ])п
у
'
у
> п зіп
п
3.224. -я. 3.225. -.3.226. - е'
4
(2 соз 2 + зіп 2). 3.227. — е"
2
(2е-1).
З 2 2 12
А
3.228. -є
-3
.3.229. — е~
а
. 3.230. -^=е
2
зіп-!-.
3
.
2
31.
-е~°(2 - а). 3.232. 0.
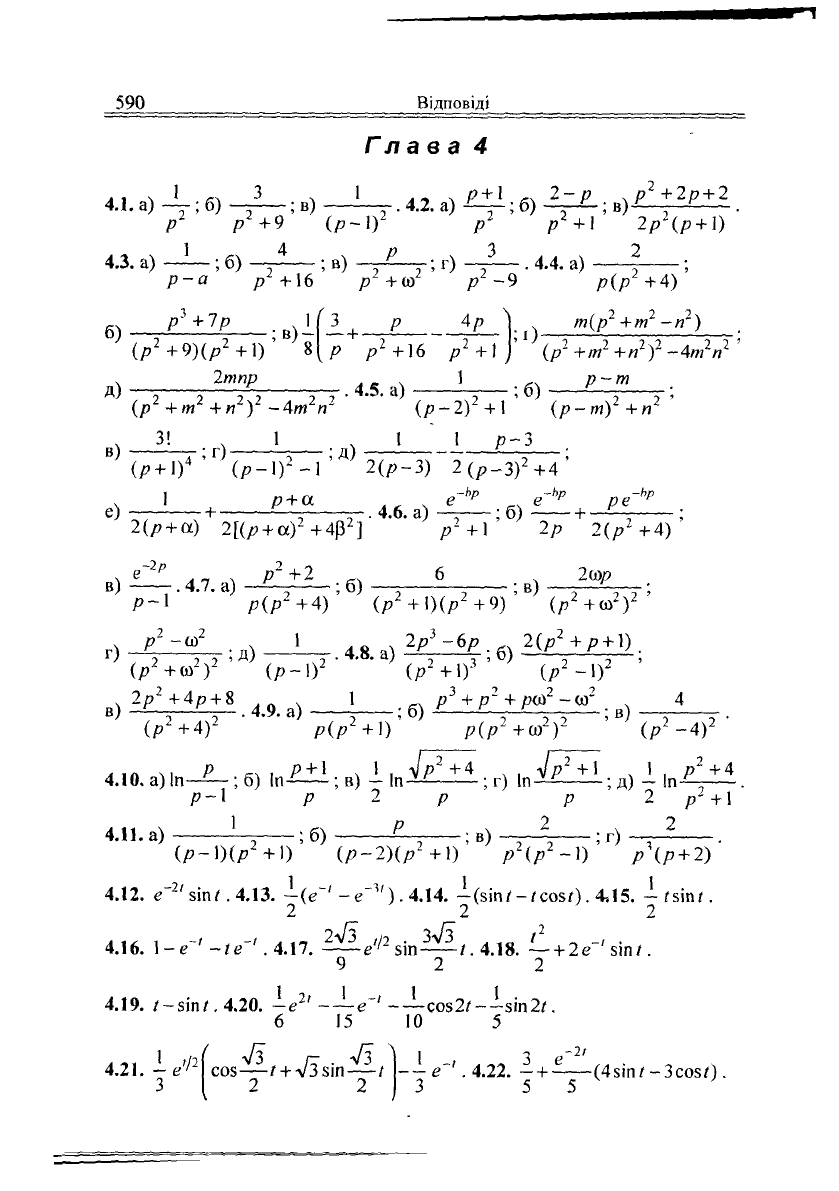
590
Відповіді
Г
лава
4
.
,
ч
1 .... 3 . 1 .„ . р
+1
_ 2 - р . о +
2 р
+ 2
4.1.
а)
—;
б)
-= ; в) .
4.2.
а)
ІЦ-;
б)
—5-^-;
в)-^
и
- -
р
2
р
2
+9
(р~\)
2
р
г
р
2
+1
2р
2
(р
+ 1)
4.3.
а)—
;б)-^—;в)
/ • г) --
3
— . 4.4. а)
2
Р~0 р
2
+16 ' р
2
+©
2
' *' р
2
-9
р(р
2
+4)
б)
/
Ч7
^ ;в)1
(р
2
+9)(р
2
+1)
8
2тир
'З
|
р 4р ^
[р
+16 р
2
+1 )
т(р
2
+т
2
-п
2
)
•
і) І •
^
' •> -) ? ? 77'
(р"
+/я +«")- -4т п
Д)
л
в ч
1
лч /5 - ОТ
-
Т
5 3-3 г-7 . 4.5. а) ; б) £— ;
(р
2
+т
2
+п
2
)
2
-4т
2
п
2
(р-2)
2
+
\
(р-т)
2
+п
2
З'
1
в
)
-——;
г
)-———-;
д)
і
і р-3
(р+1)
4
(р-1)
2
-1 2(р-3) 2(
р
-3)
2
+4
е)
1
р +
а
2(р
+ а) 2[(р +
а)
2
+4Р
2
]
~
2р
р
2
+2
4.6.
а) — ;б) —— + -~
р
2
+1
2р
2(р
2
+4)
ч
е р- +^ 6
2сор
в)
. 4.7. а) ; б) — ; в) —
и
Р-1 р(р
2
+4) (р
2
+1)(р
2
+9) (р
2
+ш
2
)
2
2
2
р
-ОТ
1
г
)
_£і _^
;
д) -—. 4.8. а) 3 ; б)
2р
3
-6р.^
2(р
2
+р
+ 1).
ІР
2
-1)
2
з)
2
^:
8
,
4
.9.
а) —і—; б) в)
4
(р
2
+4)
2
р(р'+1)
Р
+ ]
.
„ч
1
і„
л//>
2
+4
р(р
2
+ш
2
)
2
(р
2
-4)
2
'
4.10.
а) 1п-£- ; б) ; в) 1 Іп
р-1
р 2 р
4.11.
а)- ;б)- _
Р
, ;в) , \ -;г)
2
ч
, л/я +1 ч
1
і /> +
4
;
г) 1п-^ ; д) - Іп-^: .
р
2
р
2
+1
(р-1)(р
2
+1) (р-2)(р
2
+1) р
2
(р
2
-1)
р\р + 2)
4.12.
е~
2
'зіп/.4.13. -(«Г'-е
-1
').4.14. -(зіпґ-ґсоз?).
4Л5. —
Гзіпг.
2
2 2
4.16.
1-е
-
'-/є
-
'.
4.17.
~е'
/2
зіп — /. 4.18. —+
2
е
-'зіп/.
9
2 2
4.19.
/-8ІП/.4.20.
-е
2
' ~ —
е~'-—соз2/--зіп2/.
4.21.
і е'/
2
З
6
15 10
' 7з
/г
. л/з 1
соз—?
+л/З
зіп—/
З
е
-2/
-—е '.
4.22.-
+
-у—(4зіп/-3соз0 •
