Тевяшев А.Д., Литвин О.Г., Кривошеєва Г.М. та ін. Вища математика у прикладах та задачах. Ч 2

Подождите немного. Документ загружается.

§2.

Визначений інтеграл. Невласні інтеграли

Невласний інтеграл ^/(х)сіх називається абсолютно збіжним, якщо

збігається інтеграл ||/(х)|ах.

Невласний інтеграл ^/(x)с1x називається _ул<овн о збіжним, якщо він

збігається, а інтеграл || /(х)\ах розбігається.

На практиці при використанні ознак порівняння для вияснення пи-

тання про збіжність за інтеграл, з яким здійснюється порівняння, береться

У сіх _

інтеграл вигляду І —, р є К , для якого має місце твердження:

і X

^7 сіх І збігається, якщо р> 1,

•

[розбігається, якщо р<].

Такі ж властивості має інтеграл ^ —, а > 0.

Інтеграли від необмежених функцій (невласні інтеграли другого роду).

Нехай функція /(х) неперервна на відрізку [а,Ь] у всіх точках, за виклю-

ченням їх скінченної кількості, у яких функція необмежена. Точка сє [а,Ь]

називається особливою точкою функції /(х) , якщо ця функція необмежена

в цій точці, тобто /(х) —> °° при х —> с .

Розглянемо випадки, коли особливою точкою функції

/(ДЕ)

є точка

х-а;

х = Ь; х = с, а< с< Ь.

Нехай точка х = а - особлива точка функції /(х) на відрізку [а,Ь],

тобто /(х) неперервна на інтервалі (а, Ь] і Ііт /(х) = «>.

х—>а+0

Тоді за означенням, невласний інтеграл другого роду

ь ь

\/(х)сіх = Ііт

[/(х)ах.

(1.27)

£->+0

а а+Е

Якщо існує скінченна границя у правій частині формули (1.27), то не-

власний інтеграл називається збіжним. У протилежному випадку невласний

інтеграл називається розбіжним.

Геометрично невласний інтеграл (1.27) у випадку /(х) > 0 є площею

фігури, що обмежена графіком функції у = /(х), прямою х = Ь та вертикаль-

ною асимптотою х = а (рис. 1.3).

Глава 1. Інтегральне числення функцій однієї змінної

Рис. 1.3

Аналогічно, якщо точка х = Ь - особлива точка функції /(х) на від-

різку [а,Ь], то

Ь 6-Е

\Дх)сіх = Ііт \/(х)сіх. (1.28)

•'

Е->+0

а а

Якщо точка х = с

—

особлива точка функції /(х) на відрізку [а,Ь],

с є (а, Ь), то за означенням покладають

Ь с Ь

\Дх)сіх = \Дх)сіх + \Дх)сіх. (1.29)

Невласний інтеграл ^/(х)сіх вважається збіжним, якщо збігаються

обидва інтеграли, що стоять справа в (1.29).

Запишемо формули (1.27) - (1.29) з використанням первісної Р(х)

для функції /(*) на даному проміжку.

х = а - особлива точка, тоді

* ь

\Дх)сіх = Дт ІДх)ах^Р(х^

Р(Ь)-Р(

+ 0). (1.30)

х = Ь - особлива точка, тоді

* Ь-Е

• Ііт

є->+0

а а

х = с, се(а,Ь) - особлива точка, тоді

Ь с Ь

//(*) сіх = Ііт |Дх) сіх = Р(х^ = Р(Ь - 0) - Р(а). (1.31)

\Дх)сіх

=\Дх)сіх

+ \Дх)сіх = Р(х)\

^+Р(х)\

с+0

. (1.32)

§2.

Визначений інтеграл. Невласні інтеграли

Для збіжності останнього інтеграла потрібне існування скінченних

границь /^(с-О) та Р~(с + 0).

Ознаки збіжності та розбіжності невласних інтегралів другого роду

аналогічні ознакам для невласних інтегралів першого роду.

Наведемо їх для випадку, коли точка х = а - особлива точка розгля-

дуваних функцій на відрізку [а,Ь].

Теорема 1 (ознака порівняння). Якщо функції /(х) і §(х) неперерв-

ні на проміжку (а,Ь], мають особливу точку х = а і задовольняють умову

0 < Дх) < §(х), то із збіжності інтеграла |^(х)ах випливає збіжність ін-

Ь Ь

теграла |Дх) ах, а із розбіжності інтеграла |/(х)ях випливає розбіжність

а а

інтеграла ^§(х)ах.

Теорема 2 (гранична ознака порівняння). Нехай х = а - особлива то-

чка функцій Дх) і °(х) на [а,Ь] і Дх)>0, £(х)>0 на (а,Ь]. Тоді, якщо

існує скінченна границя

,•/(£)_

Ііт = А > О,

дг-»

£(х)

ь ь

то обидва інтеграли |Дх)ах та §§(х)сіх збігаються або розбігаються од-

А а

ночасно.

Теорема 3 (достатня ознака збіжності невласного інтеграла від зна-

козмінної функції). Якщо х = а — особлива точка функції Дх) і інтеграл

ь ь

||Дх)|ох збігається, то інтеграл |ДХ)ЙХ також збігається.

а а

Невласний інтеграл |/(х)ах називається абсолютно збіжним, якщо

збігається інтеграл || Дх) | ах .

Невласний інтеграл |Дх)ох називається >>мовно збіжним, якщо він

збігається, а інтеграл ||Дх)|йх розбігається.

Глава

1. Інтегральне числення функцій однієї змінної

На

практиці за інтеграл, що використовується для порівняння, часто

береться

інтеграл вигляду ї-^-, р > 0, для якого має місце твердження:

\ сіх | збігається, якщо р<1,

[розбігається, якщо р>\.

Використовуються

також інтеграли більш загального вигляду:

г сіх г сіх

та

, р > 0 ,

і(х-аУ

і(х-ЬУ

які

збігаються при р < 1 та розбігаються при р > 1.

//. Контрольні питання та завдання

Дайте означення інтегральної суми функції /(х) на від-

різку [а, Ь].

Дайте означення визначеного інтеграла.

Яка функція називається інтегровною?

Чи інтегровна функція /(х) =

—

на відрізку

[1,2];

на

відрізку [-1, 1]?

Назвіть відомі вам класи інтегровних функцій. Наведіть

приклади функцій із цих класів.

6. Перелічіть властивості визначеного інтеграла.

Чи є сума двох функцій інтегровною, якщо один з додан-

ків інтегровний, а другий - ні?

8. Відомо, що |/(х)біх>0. Чи випливає з цього, що

/(х) > 0 \7х є [а,Ь] ? Наведіть приклади.

9. Відомо, що

|/(Х)Й6С

|£(Х)ЙХ.

Чи випливає з цього,

а а

що /(х) > £(х) Ух є [а,

Ь]

? Наведіть приклади.

§2.

Визначений інтеграл. Невласні інтеграли

10.

Запишіть формулу Ньютона-Лейбніца. За яких умов вона

буде вірна?

11.

Назвіть умови, при виконанні яких будуть вірні:

а) формула заміни змінної; б) формула інтегрування части-

нами у визначеному інтегралі.

12.

Доведіть, що:

а) якщо /(х) - непарна функція, то | /(х)

сіх

= 0,

-а

а а

б) якщо /(х) - парна функція, то | /(х)

сіх

/(х) сіх, де

-а 0

/(х) - неперервна на відрізку [-а, а] функція.

13.

Доведіть, що функція Р(х) =

^/(1)сі(

є первісною для

неперервної функції /(х).

14.

Які типи невласних інтегралів існують?

15.

Дайте означення невласного інтеграла першого роду.

16.

Наведіть геометричний зміст невласного інтеграла пер-

шого роду.

17.

Дайте означення невласного інтеграла другого роду.

18.

Наведіть геометричний зміст невласного інтеграла дру-

гого роду.

19.

Який зв'язок невласного інтеграла першого роду з первіс-

ною для підінтегральної функції. Наведіть відповідні формули.

20.

Який зв'язок невласного інтеграла першого роду з первіс-

ною для підінтегральної функції. Наведіть відповідні формули.

21.

Сформулюйте ознаки збіжності невласних інтегралів

першого роду.

22.

Сформулюйте ознаки збіжності невласних інтегралів

другого роду.

23.

Наведіть приклади невласних інтегралів першого та дру-

гого роду.

Глава 1. Інтегральне числення функцій однієї змінної

///. Приклади розв'язання задач

Приклад 1. Обчислити інтеграл ^

сіх

я/С08 X

СІХ

*8*

і/ С08 X

к п Тз

Ш7-Ш-

= 1-— •<

4 6 З

Приклад 2. Знайти інтеграл |хе

*ЙХ.

• |хе * А =

и = х; сій = сіх

сЬ>

= е~

сіх; V = -е

е-2

= - хе +

\е-

сіх =

1п

Приклад 3. Обчислити інтеграл [ сіх

, х

Іпх = /

ах ,

— = аї

х = 1, / = 0

X = е, / = 1

Г/2

Л=

VI'

)

І ^

І 3 Іо З З

Приклад 4. Обчислити інтеграл |-\/^

-х

сіх

• ]7г

-X

ОТ:

X = /-51ПҐ

ОХ = ГС05ІСІІ

х = 0, / = 0

X = г, І = —

|л/г

-Л

5ІП

/ • ГС05/ ЙЇ =

_2 2

2 Г 2 і ^ г,, „ ч , /"^ Г ЗІП 2ґ

]со5^гаї

= —] (1 + сов 2г) аг =—

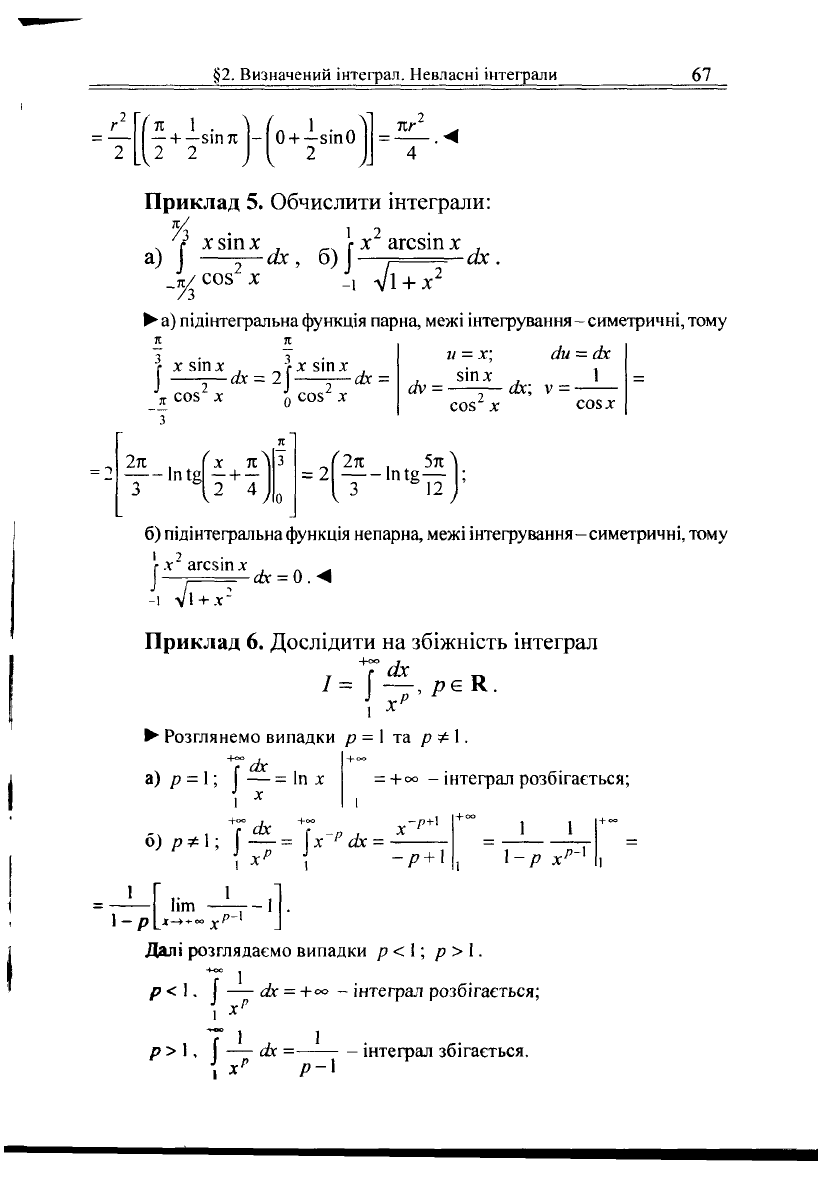
§2.

Визначений інтеграл. Невласні інтеграли

—+ —ЗІП Л

2 2

0 + -5ІП0

%г

Приклад 5. Обчислити інтеграли:

- х зіп

(•

агсзіп х

„/ СОЗ X

-1

л/ї+х

сіх

• а) підінтегральна функція парна, межі інтегрування - симетричні, тому

и = х;

- х зіпл; , Ах зіп

де

г х ьтх , -[

—

соз X

сіх

••

СОЗ X

сій

= ах

ЗІП

сіу = —

сіх;

V -

СОЗ

х созх

2л

1пІ§

(х Л

— + —

2 4

2л

5л"

б) підінтефальна функція непарна, межі інтефування - симетричні, тому

І 7

х агсзіп х ,

) і г

& = 0<

-і -уі + х"

Приклад 6. Дослідити на збіжність інтеграл

• Розглянемо випадки р =

та р * 1.

= +°° - інтефал розбігається;

б) р*\; 1^ =

сіх

= ±^

Р \ -р +

\-р х

\-р

Ііт

-1

Далі розглядаємо випадки р < 1; р > 1.

р < 1. | -у сіх = +оо - інтефал розбігається;

>\, І — ах

інтефал збігається.

Глава 1. Інтегральне числення функцій однієї змінної

Отже, невласний інтеграл

[

—

сіх

-,р>\,

збігається,

[+оо ,р<1, розбігається.

Такі ж властивості має і інтеграл вигляду

— ах, а > 0.

Отже

_*7ск_ _\Р>

-збіжний,

' і' [р <

- розбіжний.

Приклад 7. Обчислити невласний інтеграл §

хе~

сіх.

• Застосовуючи формулу Ньютона-Лейбніца, маємо:

°° 2 1

°° 2

х«Г*

ах = - - \ е'

сі(-х

)=-

сіх

Приклад 8. Знайти інтеграл [ .

_іх

+4х + 9

• Застосовуючи формулу Ньютона-Лейбніца, маємо:

ах

+ 4х + 9

~2|

~7Г

1 х + 2

=-7=гагсІ8 —р=-

л/5 У!5

СІХ

Приклад 9. Дослідити на збіжність інтеграл [ —

+ х

у проміжку інтегрування

• Підінтегральна функція /(х):

+ х

1 1 1

г,

•, тобто — < —— , хе 11,+°°) і інтеграл

менша, ніж #(х):

сіх

..10

9 її 9 9

тобто збіжний.

Тоді і інтеграл / =

—

+ х

чому / < /,. •<

за ознакою порівняння теж збіжний, при-

§2,

Визначений інтеграл. Невласні інтеграли

Приклад

10. Дослідити на збіжність інтеграл

"Т 2 +

зіп

х +

1п

х ,

!—т*—*•

•

Для порівняння з підінтегральною функцією

. 2 +

5ІПХ

ІПХ

Ах)

л/х"

візьмемо функцію з(х) = і/%/х .

2 + зіпх +

1п

х 1

Маємо

у[х

л/х

> —== > 0, хє [2,+«>),

а інтеграл [ —=• = 2 л/х І = +°° - розбігається, тоді і заданий інтеграл та-

Л/Х &

кож розбігається.

Приклад

11. Дослідити на збіжність інтеграл

сіх.

•

Підінтегральну функцію /(х) = 1п— порівняємо з функцією

£(х) = і/х

, тобто розглянемо

1п

Ііт —

1±^-= Нт

1п

X* +1

1п

+і] х

X —¥

+°О,

->0

|іт

*І±І = 1.

Згідно з граничною ознакою порівняння маємо, що оскільки інтефал

4к

—г збігається, то заданий інтефал теж збігається. -4

Приклад

12. Дослідити на збіжність інтеграл

Глава 1. Інтегральне числення функцій однієї змінної

•

Якщо р < 0 , то інтеграл не є невласним.

Якщо р > 0 , то маємо невласний інтеграл другого роду; точка х = 0

особлива точка підінтегральної функції на проміжку інтегрування.

При р =

маємо

|—

= 1п х

0+0

При р * 1 маємо

-0-(-ОО)

=+ОО

- інтеграл розбігається.

сіх

х-

р+]

їх" ~ -Р + 1

0+0

\-р х

рА

0+0

Отже,

1-р

р>\,

;Р<\.

1 [ збігається при р < 1,

—

"х - \

[ розбігається при р > 1.

Приклад

13.

Знайти інтеграл

11п х

сіх

•

Точках = 0-особлива точка підінтегральної функції на проміжку

[0,1].

|іпх сіх =

и =

Іп

х, сій = —

сЬ = сіх, V = х

Тут враховано, що

= X

•

ІП X

0+0

Гах = 0- Ііт х1пх-1 = -1

^->о+о

Ііт хіпх = {0°°} = Ііт

х->0+0

*->0+0

Іпх

—

\= Ііт

=- Ііт х = 0.^

->0+0

л:->0+0

агсзіп

СІХ

Приклад

14.

Знайти інтеграл

[ .—

о VI-

•

Точка х =

- особлива точка підінтегральної функції на проміжку [0,1 ].

[ , сіх = [агсзіп х дТагсаш х) =—(агсаш х) = 0 = — .-4

0\1-Х

о о

Приклад

15.

Дослідити

на

збіжність інтеграл

сіх