Труды Всемирного конгресса Международного общества солнечной энергии

Подождите немного. Документ загружается.

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

682

4. CONCLUSION

Taiwan University has been devoted to the development of

low-cost LHP, in cooperation with local industry. A new

manufacturing process for low-cost LHP has been

developed that leads to a cost down to less than 10USD for

a 100W LHP. The present study utilizes the low-cost LHP

to develop a new type of solar water heater. A

thermosyphon which is thermally bonded with a solar

absorber plate is used to absorb solar energy and transfer

the heat upward to the evaporator of the LHP. From that,

the heat is conducted downward to the condenser of the

LHP which is immersed in a hot water tank beneath the

solar collector. The solar water heat thus can be designed in

integral type with streamline shape which is easy to install

and has a good outlook as well as high efficiency. A

prototype was designed and fabricated in the present study.

A preliminary heat transfer test for a single unit of

thermosyphon-LHP combination shows that it is capable of

transferring the absorbed energy downward to the LHP

condenser immersed in a hot water tank. The overall

thermal resistance from the absorber plate to water is

0.34

C/W, and that of the LHP part is 0.16

C/W. Two

prototypes of the solar water heaters with 50 liters and 80

liters hot water tanks were designed according to the results

of the feasibility test. In addition, an automatic monitoring

system was designed and set up for the performance test of

these two solar water heaters based on the test standard

CNS B7277. The measured overall thermal resistance from

solar absorber plate to water is 0.369

C/W. The daily solar

water heater efficiency is 0.503. The present study has

shown that the application of low-cost LHP in solar water

heater is feasible and cost competitive. Figure 13 shows the

outlook of the new product design which is in mass

production. The capacity of water storage is 80L, and the

solar collector area is 1m

. CFD analysis has also shown

that this product can stand in a wind speed >60 m/s without

tilt-over or sliding.

Fig. 13: Product design of ISWH.

5. ACKNOWLEDGEMENT

The present study was supported by Energy Bureau,

“Ministry of Economic Affairs”, Taiwan, China, KongLin

Group, and Advanced Thermal Devices, Inc.

6. REFERENCES

(1) B.J.Huang: "Similarity theory of solar water heater

with natural circulation". Solar Energy, Vol.25(2),

pp.105-116 (1980).

(2) B.J. Huang: “Development of a low-cost LHP for

commercial application”. 13

International Heat Pipe

Conference (13

IHPC), Shanghai, China, September

21-25, 2004.

(3) Bureau of Standards, Metrology ϟ Inspection,

M.O.E.A., R.O.C. CNS B7277: Method of Test for

Solar Water Heater System1989.

PEFORMANCE OF A TWO-PHASE UNGLAZED SOLAR

EVAPORATOR-COLLECTOR

M. N. A. Hawlader*, Ye Shaochun

Department of Mechanical Engineering, National University of Singapore,

9 Engineering Drive 1, Singapore 117576

*Tel: +65-6516 2218, Fax: +65-6779 1459, email: mpehawla@nus.edu.sg

ABSTRACT

In this study, the performance of a two-phase unglazed

solar evaporator-collector in a heat pump solar cooling,

water heating and drying system is investigated. This type

of collector can be locally made and relatively much

cheaper than the conventional collector. Refrigerant

R-134a is used as the working fluid due to the better

thermodynamic and environmental performance. A

transient two-dimensional mathematical model of the

evaporator-collector has been developed to predict

temperature distribution and useful energy gain. A series

of experiments were performed under the meteorological

conditions of Singapore. Both experimental and analytical

results show the fact that the two-phase unglazed solar

evaporator-collector, instead of losing energy to the

ambient, gained a significant amount due to low operating

temperature of the collector. As a result, the collector

efficiency attains a value greater than 1, when

conventional collector equation is used. With this

evaporator-collector, the system can be operated even in

the absence of solar radiation. Experiments with a header

type parallel tube evaporator-collector and serpentine

collector indicate a better performance of serpentine one.

This analysis shows that the two-phase unglazed solar

evaporator-collector has good potential for application in

the tropics.

1. INTRODUTION

In view of the growing global energy needs and concern for

environmental degradation, the possibility of running

thermal system using the energy from the sun is receiving

considerable attention in recent years. In addition, heat

pump is widely used in heating applications. A concept

named direct expansion solar-assisted heat pump

(DX-SAHP) was first proposed in an experimental study by

Sporn and Ambrose[1]. Based on these studies, Chaturvedi

et al.[2] performed an investigation on the steady state

thermal performance of a direct expansion solar-assisted

heat pump and indicated that this system offers significant

advantage in terms of superior thermal performance.

Various studies have been conducted to investigate different

types and applications of direct expansion solar-assisted

heat pump. Hawlader et al.[3] used refrigerant 134a in the

heat pump for water heating application and the evaporator

was used as a solar collector leading to a significant

improvement in COP. Lu et al. [4] used R-22 as the

working fluid under the meteorological condition of

Australia. They also simulated and compared the

performance of air-source heat pump and solar heat pump

in eight cities of Australia. Huang and Lee [5] also

developed a heat pump solar water heater. Hawlader et al.[6]

developed a solar-assisted heat-pump dryer and water

heater. The COP of the system was about 5.0.

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

684

Solar evaporator-collector is the essential component in a

direct expansion solar-assisted heat pump system. The

concept of un-glazed solar evaporator collector was first

proposed and investigated by Chaturvedi et al.[7]

The Simple structure of the un-glazed solar collector makes

it an economical type of solar collector. However, its

performance is highly dependent on the environment. Many

authors [8-10] reported that, for the ambient temperature of

above 25°C, the evaporator could be operated at an

elevated temperature. Hawlader et al. [3] performed

analytical and experimental studies on a solar assisted heat

pump using unglazed, flat plate solar collectors, known as

an evaporator-collector, using a steady-state one-

dimensional mathematical model

In current study, the performance of a two-phase unglazed

solar evaporator-collector in a heat pump solar cooling,

water heating and drying system is investigated. The

evaporator-collector is made of a copper absorber plate

coated with black paint with no glazing. Underneath the

plate, serpentine copper tubes are brazed to enable the

refrigerant to flow. This type of collector can be locally

made and relatively much cheaper than the conventional

collector. Refrigerant R-134a is used as the working fluid

due to the better thermodynamic and environmental

performance. A proto-type of the system has been

fabricated and installed at the National University of

Singapore. The three functions, which are cooling, water

heating and drying, can be served simultaneously or

independently. A series of experiments were performed

under the meteorological conditions of Singapore to

validate the model.

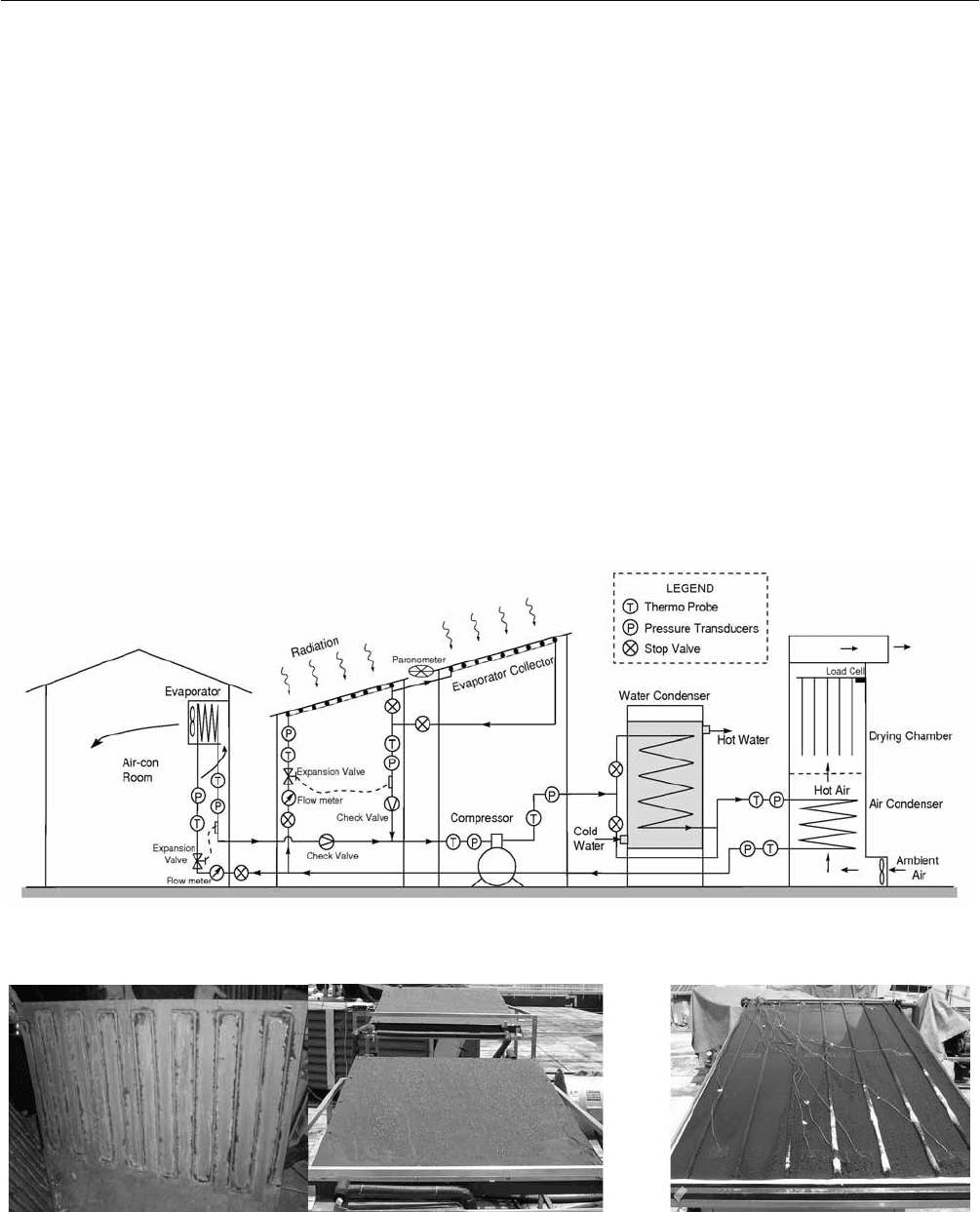
An integrated solar assisted heat pump system was

designed and built, as shown in Fig. 1, and operated in the

meteorological conditions of Singapore. Two

evaporator-collectors were connected in series. A copper

Fig. 1: Schematic diagram of an integrated solar heat-pump system.

Fig. 2: Photograph of the serpentine type evaporator-collector and header type evaporator-collector.

3 SOLAR COLLECTOR TECHNOLOGIES AND SYSTEMS

685

tube of 9.52 mm diameter was soldered at the back of each

absorber plate in serpentine form. Adequate insulations

were provided at the back of the collector but no glass

cover was used on the top surface i.e. unglazed collector.

There is a bypass line from the exit of the first

evaporator-collector to the exit of second

evaporator-collector, which remains closed or open

depending on the solar irradiation. Refrigerant R-134a is

used as the working fluid due to the better thermodynamic

and environmental performance.

A thermostatic expansion valve is used for the system, which

maintains constant superheat at the inlet of the compressor

by regulating the mass flow rate of refrigerant with the help

of a feeler bulb. Actually, the feeler bulb is a remote bulb of

the thermostatic expansion device that controls the degree of

superheat by controlling the pressure. An open

type-reciprocating compressor is used for the system, which

is directly coupled to a three-phase induction motor.

The three applications (air-conditioning, water heating and

drying) of this system can be served simultaneously or

independently. A frequency inverter is utilized to vary the

compressor speed, to have proper matching between the

evaporator load (cooling requirement) and condenser load

(heating requirement) and thus improves the efficiency.

Different motor speeds in different operating conditions

lead to different refrigerant mass flow rate in the

evaporator-collector

The details of the evaporator-collectors are shown in Figure 2.

MATHEMATICAL MODELING AND SIMULATION

A transient mathematical model of the system has been

developed. Two-dimensional simulation is applied in the

part of evaporator-collector to obtain more accurate

collector performance prediction. By considering an

element of the collector, a two-dimensional partial

differential equation is developed to describe the collector

performance, as shown in equation 1

TT T

ktxyδα

∂∂ ∂

++=

∂∂∂

(1)

where

() ( )qI UTTτα=−− and 1τ =

Equation 1 is solved by making use of Crank-Nicholson

method and appropriate boundary conditions.

Using Crank-Nicholson method, the governing equations

for the evaporator-collector are expressed as:

TTT

xxx

TT TTT T

yy y

TTT

⎛⎞

∂∂∂

⎜⎟

∂∂∂

⎝⎠

⎛⎞

+− +−

⎜⎟

ΔΔ

⎝⎠

⎛⎞

+− +−

∂

⎜⎟

∂Δ Δ

⎝⎠

−∂

∂Δ

The Finite difference approximation for the partial

differential equation is derived as:

()

TTTT T

TTTT T IUT

rr r

⎛⎞

++++−−−

⎜⎟

⎝⎠

⎛⎞

=− + + + + + − − +

⎜⎟

⎝⎠

where

δδ

ΔΔ

and

ρδ

After setting the initial condition, variation of temperature

distribution on the evaporator-collector can be calculated

by Gauss-Seidel iteration method using the finite difference

approximation.

RESULTS AND DISCUSSION

Results were obtained for both simulation and experimental

data. Meteorological data for a typical day in Singapore is

shown in Figures 3.1 and 3.2.

In Fig. 4, predicted useful energy gain (Q

) by collector

was plotted against time. Useful energy gain(Q

) is the

combination of energy gain from irradiation and the energy

gain from ambient. While the energy gain from ambient,

surrond

is mainly effected by ambient temperature. It shows

that predicted Q

has a reasonably good agreement with

experimental values. As seen from Figure 4, Q

shows a

slightly declining trend with the reduction of irradiation.

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

686

Fig. 3.1: Variation of solar radiation and ambient

temperature with time for a typical day in

Singapore.

0.2

0.4

0.6

0.8

9:00 10:00 11:00 12:00 13:00 14:00 15:00 16:00 17:00

Time

Wind Speed(m/s)

Relative Humidity

Wind Speed

Fig. 3.2: Variation of relative humidity and wind speed with

time for a typical day in Singapore.



















         

7LPH

(QHUJ\JDLQ:

4XVLPXODWLRQ 4VXUUR QG

4XH[SHULPHQW 4UDGLD WLRQ

Fig. 4: Variation of useful energy gain of the evaporator-

collector.

For high irradiation level, the unglazed solar

evaporator-collector absorbed almost equivalent energy

from both irradiation and the ambient. However, it

absorbed much more energy from the ambient than that

from irradiation when the level of radiation is lower than

600W/m

,as shown in Figures 3.1 and 4. This property

enables the unglazed evaporator-collector to supply

sufficient energy even at cloudy day and night.

0.2

0.4

0.6

0.8

1.2

1.4

1.6

9:00 10:0011:0012:001 3:0014:0015 :0016:0017:00

Time

Efficiency

200

400

600

800

1000

Radiation(W/m2)

Efficiency

Radiation

Fig. 5: Variation of solar collector efficiency and solar

radiation with time.

Solar collector efficiency is defined as the ratio of the

useful energy gain to the total incident solar radiation. As

shown in Figure 4, the total useful energy gain is relatively

constant when radiation is fluctuating. This feature of

unglazed solar evaporator collector makes the collector

efficiency to decline when radiation increases. However,

due to the energy gain from ambient, the collector

efficiency can be more than 1 at the condition of low level

of radiation.

0 4 8 12 16 20 24

Tube length(m)

Plate temperature(C)

0.2

0.4

0.6

0.8

1.2

Vapour quality

plate T(mean)

Quality

Fig. 6 Mean plate temperature and vapour quality against

the tube length.

Fig. 6 shows the simulation result of mean plate

temperature and vapour quality against the tube length

when the radiation at 700W/m

and ambient temperature at

C. At two phase flow region, where vapour quality is

less than 1, plate temperature is much lower than the

ambient temperature. This temperature difference causes

the energy gain from ambient. However, plate temperature

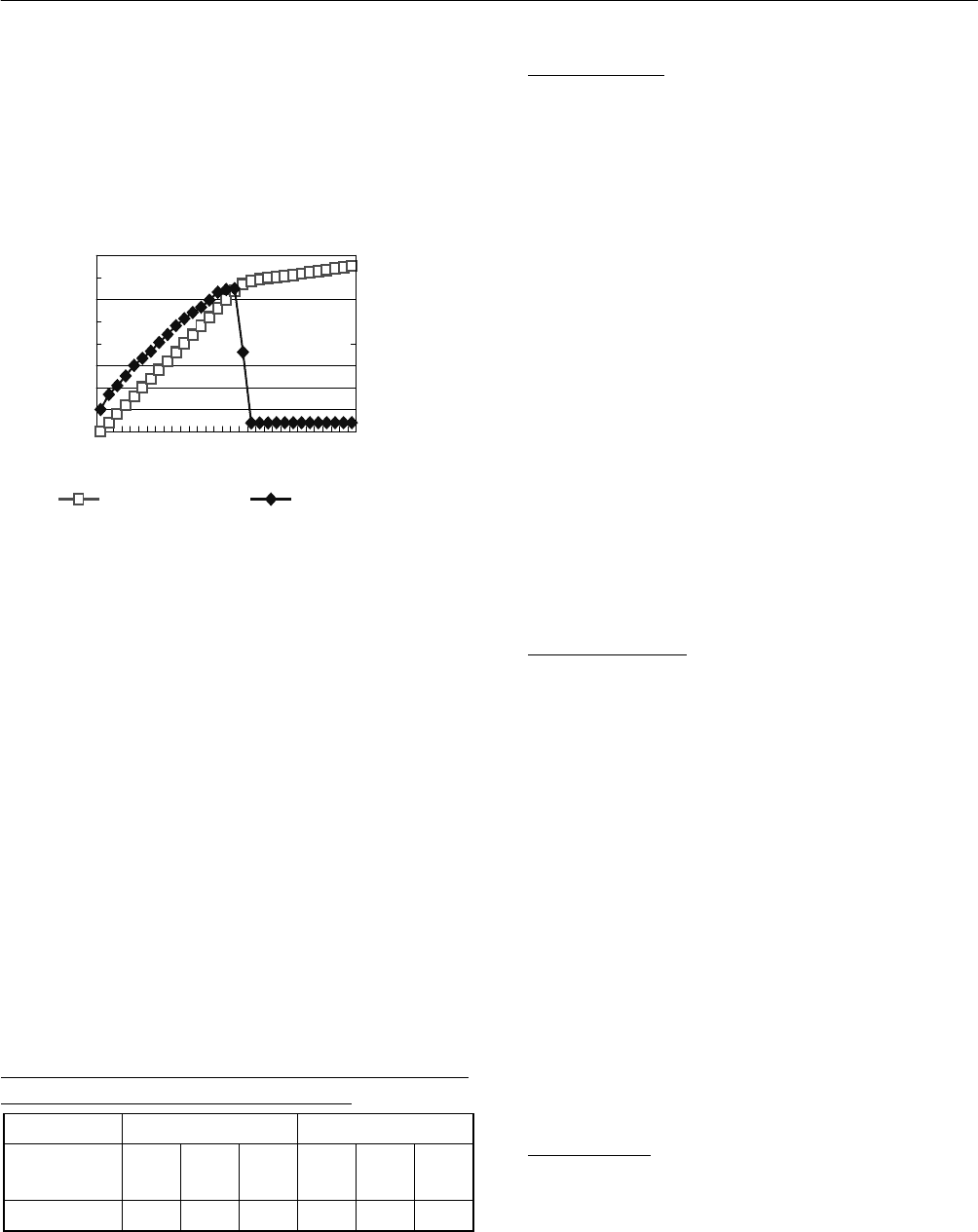
3 SOLAR COLLECTOR TECHNOLOGIES AND SYSTEMS

687

rapidly increased and exceed the ambient temperature when

refrigerant reached pure vapour region.

As shown in figure 7, the increasing rate of useful energy

gain dropped dramatically due to the heat transfer

coefficient dropped to a lower value in single phase

(saturated vapour) region.

500

1000

1500

2000

2500

3000

3500

4000

0 4 8 12 16 20 24

Tube length(m)

Useful energy gain(W)

500

1000

1500

2000

Heat transfer coeff(W/m2

Usefull heat heat tansfer coeff

Fig. 7: Heat transfer coefficiency in the tube and useful

energy gain against the tube length.

It was also found that the length of two phase flow region

reduced when radiation increased or mass flow rate reduced.

By adjusting the mass flow rate, the ratio of two phase flow

region length to the total length can be controlled in

different meteorological condition.

Besides the serpentine type solar evaporator-collector,

header type is another common type for solar collector. The

performance of these to types of two-phase unglazed solar

evaporator-collector is shown as follows:

Both the experiments were conducted under radiation level

at 700W/m

. At the same radiation level and for same

collector area, the serpentine type collector has higher

efficiency than header type with parallel tubes, as clearly

shown in Table 1.

TABLE 1: COMPARISON OF BOTH SERPENTINE

TYPE AND HEADER TYPE COLLECTOR

Area:1.5m

Serpentine type Header type

Compressor

Speed, rpm

450 600 750 450 600 750

Efficiency 1.18 1.11 1.08 0.87 0.85 0.83

4. CONCLUSIONS

A two-dimensional mathematical model of the

evaporator-collector has been developed to predict

temperature distribution and useful energy gain. To validate

the model, experiments were conducted under the

meteorological conditions of Singapore. Both experimental

and analytical results show the fact that the two-phase

unglazed solar evaporator-collector, instead of losing energy

to the ambient, gained a significant amount from the

surrounding air due to low operating temperature of the

collector. Analytical results show that both heat transfer

coefficient and energy gain in two phase region of collector

are much higher than those in single phase (saturated vapour)

region. The length of two phase region increases while the

radiation decline. Experiments with a header type parallel

tube evaporator-collector and serpentine collector indicate a

better performance of serpentine one. This analysis shows

that the two-phase unglazed solar evaporator-collector has

good potential for application in the tropics.

5. NOMENCLATURE

Abbreviation Description Unit

Specific heat capacity kJ/K

I Solar radiation W/m

k Thermal conductivity W/mK

m Mass flow rate kg/s

Useful energy gain W

t Time s

T Temperature K

Heat loss coefficienct W/ m

α Solar absorptance dimensionless

τ Transmittance dimensionless

ρ Density kg/m

δ Plate thickness m

Subscripts

a air

6. REFERENCES

(1) P. Sporn and E. R. Ambrose, The Heat Pump and Solar

Energy Proc. Worm Symp. Appl. Solar Energy, Phoenix,

Arizona, Nov 1-5, 1955

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

688

(2) S.K. Chaturvedi, D.T.Chen and Kheireddine, A,

Thermal performance of a direct expansion solar

assisted heat pump. Energy Conversion and

Management, v 39, n 3-4, Feb.-March 1998, p 181-91

(3) M.N.A. Hawlader, S.K. Chou, and M.Z. Ullah, The

performance of a solar assisted heat pump water

heating system, Applied Thermal Engineering, Volume

21, Issue 10, Pages 1049-1065

(4) Lu, A., Charters, W.W.S. and Chaichana, C. Solar heat

pump systems for domestic hot water, Solar Energy Vol.

73, No. 3, pp. 169–175

(5) B.J. Huang and C.P. Lee, Long-term performance of

solar-assisted heat pump water heater, Renewable

Energy, Volume 29, p633–639.

(6) M.N.A. Hawlader, S.K. Chou, K.A. Jahangeer, Rahman,

S.M.A. and Eugene Lau K. W. Solar-assisted heat-

pump dryer and water heater, Applied Energy, Volume

74, Issues 1-2 , Pages 185-193

(7) S.K.Chaturvedi, F.B.G. Chata and A.Almogbel,

Analysis of a direct expansion solar assisted heat pump

using different refrigerants, Energy Conversion and

Management, v 46, n 15-16, Sept. 2005, p 2614-24

(8) E.A. Kush, Performance of heat pumps at elevated

evaporating temperatures with application to solar input.

Journal of Solar Energy Engineering 102 (1980), pp.

203–210.

(9) G.L. Morrison and D. Gilliaert, Unglazed solar

collector performance characteristics. Journal of Solar

Energy Engineering 114 (1992), pp. 194–200.

Abstract-INSPEC

(10) M.P. O'Dell, J.W. Mitchell and W.A. Beckman,

Design method and performance of heat pumps with

refrigerant filled collectors. Transactions of the

ASHRAE 89 (1) (1983), pp. 519–525.

AN EXPERIMENTAL STUDY ON THE HEAT TRANSFER CHARACTERISTICS OF THE

HYBRID SOLAR RECEIVER FOR A DISH CONCENTRATING SYSTEM

MyeongCheol Kang

Korea Institute of Energy Research

P.O. Box 305-343

Daejeon, Korea

mckang21@kier.re.kr

JinSoo Kim

Korea Institute of Energy Research

P.O. Box 305-343

Daejeon, Korea

jinskim@kier.re.kr

YongHeack Kang

Korea Institute of Energy Research

P.O. Box 305-343

Daejeon, Korea

yhkang@kier.re.kr

NackJoo Kim

Seoul National University of Technology

P.O. Box 139-743

Seoul, Korea

nackjoo@snut.ac.kr

SeongYeon Yoo

BK21 Mechatronics Group at Chungnam National

University

P.O. Box 305-764

Daejeon, Korea

syyooh@cnu.ac.k

JinHeack Kim

BK21 Mechatronics Group at Chungnam National

University

P.O. Box 305-764

Daejeon, Korea

mcple80@cnu.ac.kr

ABSTRACT

The dish/stirling system is used to convert solar energy

directly to electricity. Therefore, in order to improve

economical efficiency of a solar power system, the stirling

unit must be operated continuously. For continuous

operation of the stirling unit, the receiver must be

continuously provided with thermal energy from solar as

well as additional combustion heat. It is possible for a

hybrid solar receiver system equipped with an additional

combustion system to be operated 24 hrs/day.

A hybrid solar receiver adopted heat pipe heat transfer

mechanism was designed and manufactured to supply the

thermal energy to the stirling engine.

The hybrid receiver system was tested in a gas-only mode

to investigate heat transfer characteristics at inclination

angles varying from 0 deg to 30 deg and the ratios of the

aperture diameter to cavity diameter of 0(closed cavity) and

1(open cavity). The increase in temperature in the case of a

closed cavity is higher than an open cavity, but

temperatures in all cases rise in proportion to the input

thermal load. In the case of the open cavity, the thermal

resistances decreased in proportion to input thermal load

and inclination angle, but it was 1~3 times higher than

those of the closed cavity. The evaporation and

condensation heat transfer coefficient increased linearly

with input thermal load. The evaporation heat transfer

coefficient increased in proportion with input thermal load

and inclination angle in the closed cavity.

1. INTRODUCTION

A dish type solar concentrating system consists of a

parabolic concentrator and a receiver. In order to achieve

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

690

high temperature from solar energy, it is essential to

efficiently reflect the solar rays in the concentrator and to

minimize thermal losses in the cavity receiver. For

idealizing the design of a receiver, the characteristics of the

concentrator, the shape and size of flux distributions in the

focal plane, should be considered. The design of the solar

receiver is a key technology and one of the most difficult

properties of developing dish-type solar power systems.

However, the solar energy has a fundamental disadvantage

of inconsistent power density, depending on weather

conditions and seasons.

The hybrid receiver system is required to improve

economical efficiency of a solar power system using solar

and additional combustion heat. The new concept of

developing a receiver for continuous operation of the stirling

unit is required and technology of the heat pipe is presented.

The heat pipe allows a separation of the different heat

transfer surfaces, absorber surface, combustion surface, and

stirling head[1]. A heat pipe receiver has the advantage of

excellent heat transfer mechanisms, and non-uniform heat

fluxes can be tolerated much better than with the tube type

receiver[2]. Laing D. successfully developed and tested for

the hybrid heat pipe receiver. Maximum system efficiency

in solar-only mode had been 16%, in gas-only mode 17%,

and in hybrid mode 15%. Hartenstine, et al. designed a

hybrid receiver based on numerical simulations and small

scale tests, and fabricated a hybrid receiver with the 3

burners to operating simultaneously[4].

In this paper, a hybrid solar receiver adopted heat pipe heat

transfer mechanism was designed and manufactured to

supply solar energy as well as additional combustion heat

to the stirling engine. The hybrid receiver system was

tested in gas-only mode to investigate the heat transfer

characteristics.

2. EXPERIMENTAL APPARATUS AND METHODO-

LOGY

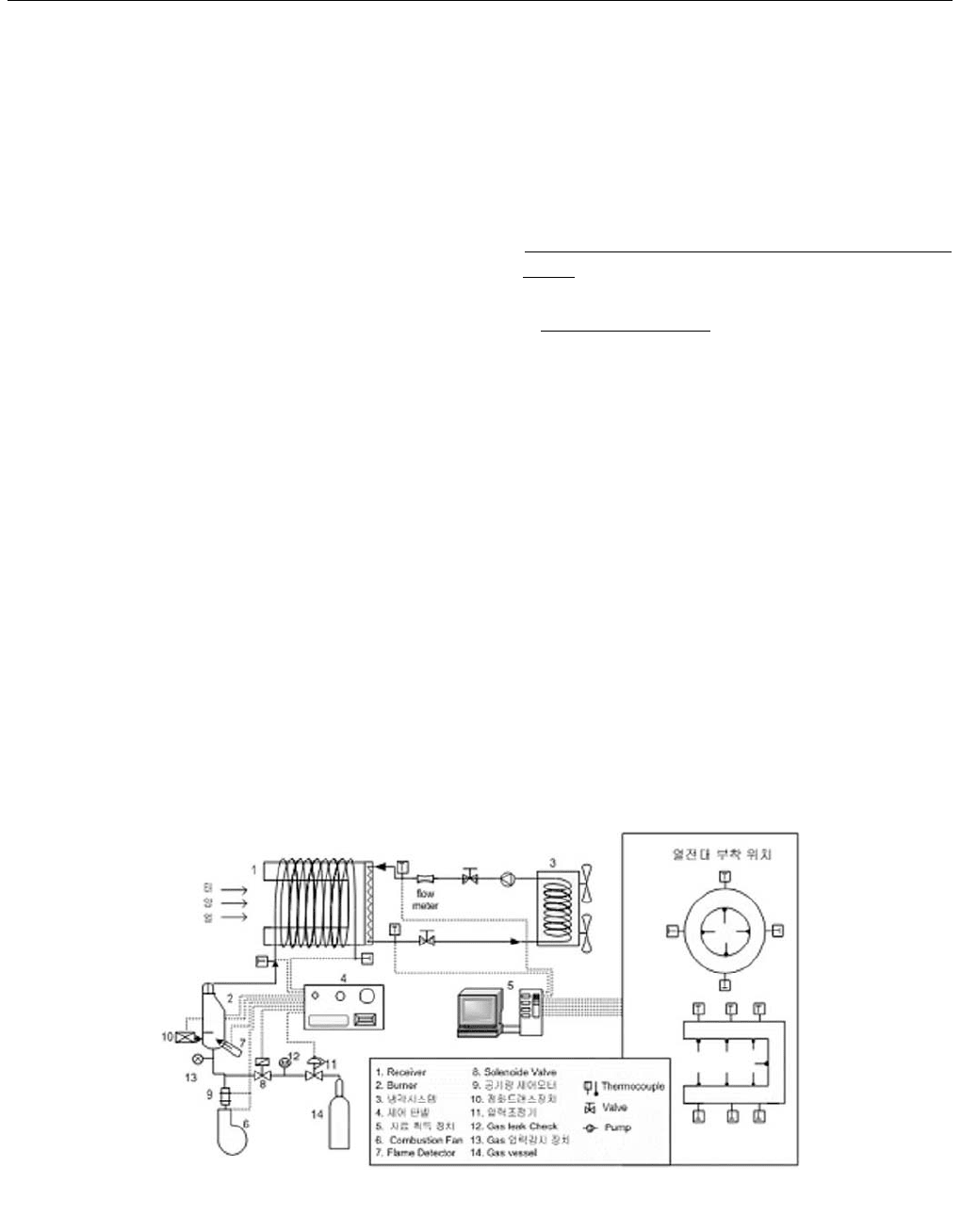
2.1 Hybrid Solar Receiver

The hybrid receiver using heat pipe was manufactured to

supply thermal from solar in cavity and combustion heat in

out surface wall. The heat pipe was designed for a total

thermal load of 35 kW in the operating temperature range

700ଇ to 800ଇ vapor temperature and used working fluid

of sodium. The heat pipe has a double walled vessel and

consists of a solar heat input, combustor heat input, and

heat output to stirling head, it is realized by using three

different heat transfer surfaces.

The cavity diameter is 216 mm and the diameter of the

outer heat pipe mantle is 315 mm. The outer heat pipe

mantle serves as a heat transfer surface for the gas heat

flow. The heat pipe container is made of stainless steel. All

capillary structures are made of a stainless steel screen and

spotted in place. Fig. 1 shows the schematic of experimental

apparatus and receiver thermocouples locations. A picture

Fig. 1: Schematic of experimental apparatus and receiver thermocouples locations.

3 SOLAR COLLECTOR TECHNOLOGIES AND SYSTEMS

691

of the experimental apparatus with receiver, combustion

system, and cooling system is shown in Fig. 2.

Fig. 2: Experimental apparatus with receiver, combustion

system, and cooling system.

The natural gas burner will supply the high temperature of

combustion to the hybrid heat pipe receiver. The

combustion systems consist of a burner, combustion fan,

flame detector, ignition transformer, etc. The burner will be

fired tangentially into the combustion chamber. The burner

is equipped with a air damper motor and gas solenoide

valve to control the flowrate of air and gas. The flame

holder is located in the side part of the heat pipe outer wall

and combustion heat is circulated through the flow path

line.

The hybrid receiver performance will be verified through

ground testing by gas fired heat. To investigate heat transfer

characteristics from the hybrid receiver, it was tested at

inclination angles varying from 0 deg to 30 deg(cavity

facing down). The ratios of the aperture diameter to cavity

diameter of 0(closed cavity) and 1.0(open cavity) were

used as well. This paper has been constructed to measure

temperature variation in cavity surface and to analyze

thermal resistances, and the evaporation and condensation

heat transfer coefficient in all cases(open and closed

cavity).

3. RESULTS AND DISCUSSIONS

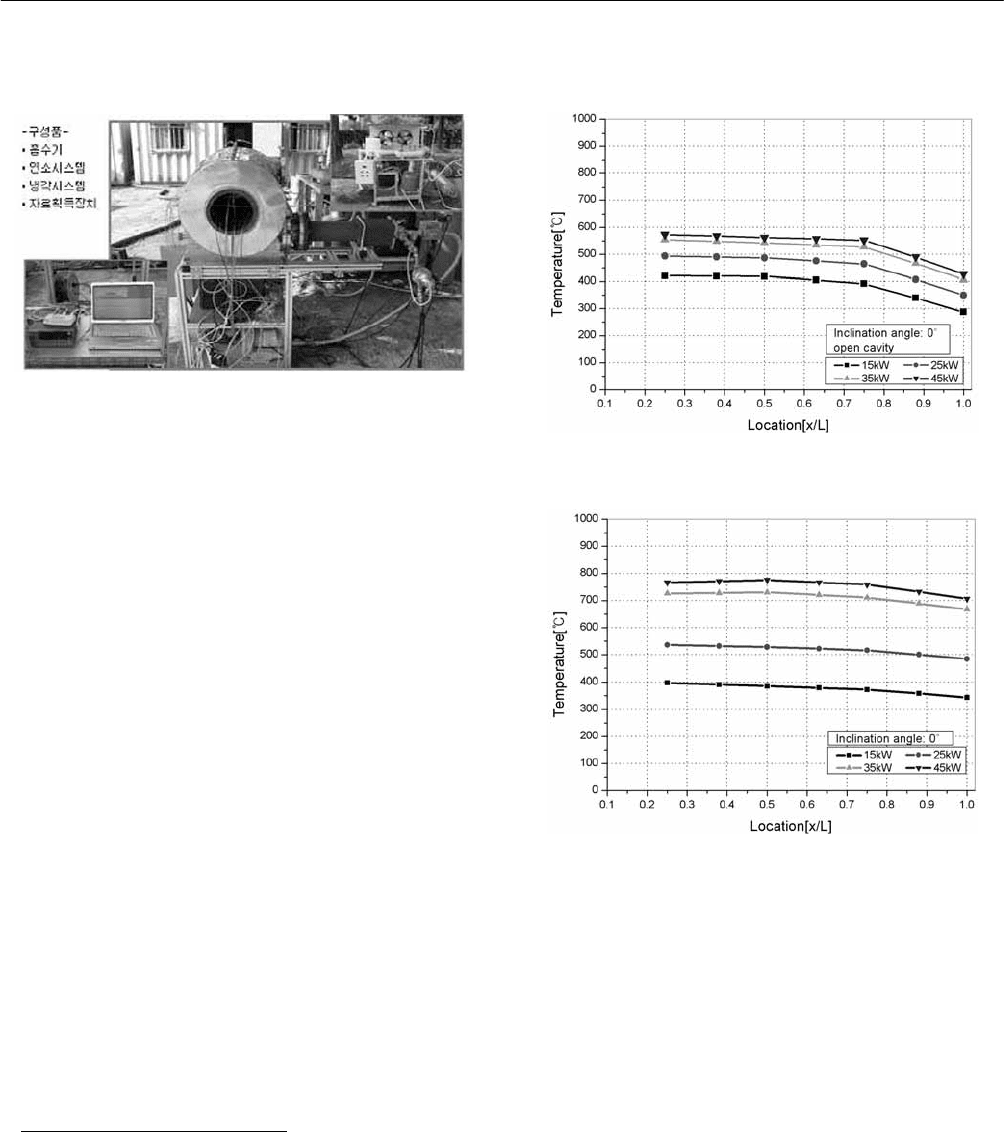
Fig. 3 and Fig. 4 show the temperature distribution along

length of cavity surface at 0 deg in an open and closed

cavity. The increase in temperature in the case of a closed

cavity is higher than an open cavity, but temperature in all

cases rise in proportion to the input thermal load. The

temperature difference along the length of the open cavity

surface was higher than that of the closed cavity.

Fig. 3: Temperature distribution along length of cavity

surface at 0 deg(open cavity).

Fig. 4: Temperature distribution along length of cavity

surface at 0 deg(closed cavity).

Fig. 5 and Fig. 6 show the thermal resistances variation

with increasing input thermal load. In case of the open

cavity, the thermal resistances decreased in proportion to

input thermal load and inclination angels, but it was 1~3

times higher than those of the closed cavity.

The variation of evaporation heat transfer coefficient in all

cases is shown in Fig. 7 and Fig. 8, respectively. Fig. 9 and

Fig. 10 show variation of condensation heat transfer

coefficient in all cases. The evaporation and condensation

heat transfer coefficient increased linearly with input

thermal load in the open cavity. The evaporation heat

transfer coefficient in proportion with input thermal load

and inclination angle in the closed cavity. The condensation

Труды Всемирного конгресса Международного общества солнечной энергии - 2007. Том 2

Подождите немного. Документ загружается.