Управление стоимостью бизнеса и подготовка кадров по ценообразованию и оценочной деятельности. Сборник докладов

Подождите немного. Документ загружается.

стичные прогнозы, забывая о том, что доходность бизнеса может зависеть

даже от моды.

Точность метода дисконтирования денежных потоков очень зависит

от корректной оценки нормы доходности. В ее качестве используется

средневзвешенная стоимость капитала компании – WACC. Использование

WACC позволяет учесть тот факт, что в случае наиболее дешевого долго-

вого финансирования средневзвешенные затраты на капитал падают про-

порционально доле заемного капитала. Если же компания не использует

заемных средств вообще, то расчет сведется к определению стоимости

собственного капитала.

Вокруг того, как считать ставку дисконтирования, российские спе-

циалисты ведут затянувшиеся споры. Использовать данные российского

фондового рынка для модели САРМ (модель оценки капитальных акти-

вов) пока не удается. Поэтому берутся цифры с рынка США и модифици-

руются в сторону увеличения. Условно безрисковыми считаются россий-

ские еврооблигации, эмитированные государством. Кроме того, делаются

поправки на риск конкретной компании, зависящие от прозрачности ее

структуры, качества управления, стабильности финансового положения.

Конечно, расчет стоимости бизнеса с использованием доходного подхода

весьма сложен. Можно упустить какой-то риск или, наоборот, учесть его

дважды. Очень часто к безрисковой ставке, рассчитанной до доходности

ценных бумаг, содержащей страновой риск, повторно прибавляется по-

правка на российский страновой риск. Зато при корректном расчете ре-

зультаты будут получены самые точные.

Оценщик должен по возможности использовать все три подхода к

определению стоимости, имеющихся в его распоряжении. В действитель-

ности ни один из подходов не является лучше или хуже другого; только

конкретные факты и обстоятельства оценочного задания делают один из

методов более подходящим для применения, чем другие.

Правильная оценка позволяет компании привлечь в свой бизнес хо-

рошие инвестиции, выйти на фондовый рынок и на международные рынки

капитала.

К. Н. Гнездилов, аспирант

кафедры ценообразования

и оценочной деятельности СПбГУЭФ

Выбор вида уравнения регрессии в оценке недвижимости

На сегодняшний день все больше оценщиков применяют корреляци-

онно-регрессионный анализ в своих расчетах. Но зачастую выбор регрес-

сионной модели ограничивается простым линейным уравнением.

Если в большинстве случаев оцифровать характеристики объекта

оценки и объектов аналогов не представляет труда, то выбор модели

(уравнения) регрессии может вызвать сложности у рядовых оценщиков.

Основными этапами регрессионного анализа являются:

1. Выбор независимых переменных, оказывающих существенное влия-

ние на зависимую переменную.

2. Оценка параметров уравнения регрессии (параметризация модели).

3. Выбор вида уравнения регрессии (спецификация модели).

4. Измерение влияния отдельных факторов на зависимую переменную.

5. Оценка статистической надежности регрессионной модели (верифи-

кация модели).

Выбор формулы связи переменных называется спецификацией урав-

нения регрессии. В случае парной регрессии выбор формулы обычно осу-

ществляется по графическому изображению реальных статистических

данных в виде точек в декартовой системе координат (графический метод

выбора уравнения регрессии), которая называется корреляционным полем

(или диаграммой рассеивания)

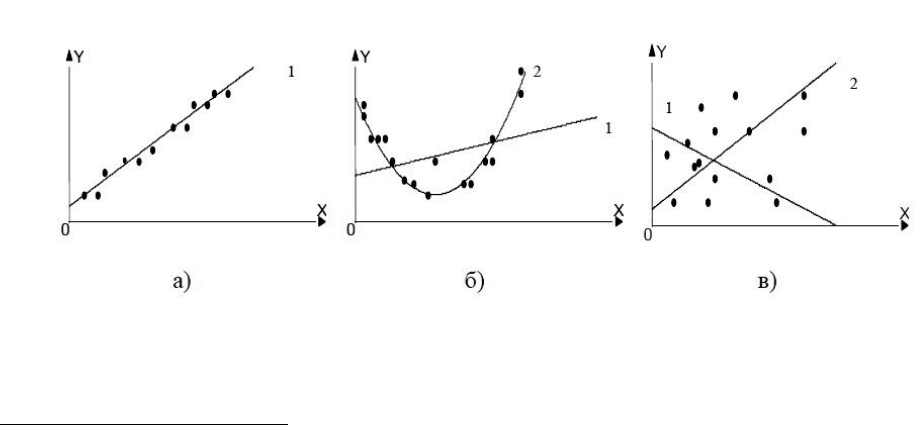
На рис. 1 представлены три ситуации

а) взаимосвязь между Х и Y близка к линейной, и прямая достаточно

хорошо соответствует эмпирическим точкам;

б) реальная взаимосвязь между Х и Y, скорее всего, описывается

квадратичной функцией, и какую бы мы ни провели прямую (например,

линия 1), отклонения точек наблюдений от нее будут существенными и

неслучайными;

в) явная зависимость между Х и Y отсутствует. В данном случае, ка-

кую бы мы не выбрали форму связи между переменными, результаты спе-

цификации и параметризации модели будут неудачными.

Рис. 1

http://www.metrologie.ru/qualitymanagement-stat25.htm.

Баранова Т. А. Многомерные статистические методы. Регрессионный анализ. – Ива-

ново: Ивановский гос. химико-технический ун-т, 2007.

Существует и метод перебора различных уравнений

, сущность ко-

торого заключается в том, что большое число уравнений (моделей) рег-

рессии, отобранных для описания связей какого-либо социально-

экономического явления или процесса, реализуется на ЭВМ с помощью

специально разработанного алгоритма перебора с последующей статисти-

ческой проверкой, главным образом на основе t-критерия Стьюдeнта и F-

критерия Фишера. Способ перебора является достаточно трудоемким и

связан с большим объемом вычислительных работ.

Задача определения функциональной зависимости, наилучшим обра-

зом описывающей распределение объектов на диаграмме рассеивания,

связана с преодолением ряда принципиальных трудностей. В общем слу-

чае для стандартизованных данных функциональную зависимость показа-

теля от параметров можно представить в виде

y = f (u1, u2, ...up) + e,

где f – заранее не известная функция, подлежащая определению;

e – ошибка аппроксимации.

Указанное уравнение принято называть выборочным уравнением

регрессии y на u. Это уравнение характеризует зависимость между вариа-

цией показателя (стоимость объекта оценки) и вариациями (ценообра-

зующих) факторов. А мера корреляции измеряет долю вариации показате-

ля, которая связана с вариацией факторов. Иначе говоря, корреляцию по-

казателя и факторов нельзя трактовать как связь их уровней, а регресси-

онный анализ не объясняет роли факторов в создании показателя

Еще одна особенность касается оценки степени влияния каждого

фактора на показатель. Регрессионное уравнение не обеспечивает оценку

раздельного влияния каждого фактора на показатель, такая оценка воз-

можна лишь в случае, когда все другие факторы не связаны с изучаемым.

Если изучаемый фактор связан с другими, влияющими на показатель, то

будет получена смешанная характеристика влияния фактора. Эта характе-

ристика содержит как непосредственное влияние фактора, так и опосредо-

ванное влияние, оказанное через связь с другими факторами и их влияни-

ем на показатель

В регрессионное уравнение не рекомендуется включать факторы,

слабо связанные с показателем, но тесно связанные с другими факторами.

Не включают в уравнение и факторы, функционально связанные друг с

другом (для них в этом случае коэффициент корреляции равен 1). Включе-

ние таких факторов приводит к вырождению системы уравнений для оцен-

Теория статистики: Учебник / Под ред. проф. Р. А. Шмойловой.

Ходасевич Г. Б. Обработка экспериментальных данных на ЭВМ. – СПб.: Санкт-

Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-

Бруевича.

Чернова Т. В. Экономическая статистика: Учебное пособие. – Таганрог: Изд-во

ТРТУ, 1999.

, i =1, 2, … , n.

ки коэффициентов регрессии и к неопределенности решения. Поэтому не-

обходимо провести корреляционный анализ ценообразующих факторов.

Функция f должна подбираться так, чтобы ошибка e в некотором

смысле была минимальна. Существует бесконечное множество функций,

описывающих распределение аналогов абсолютно точно (e = 0), т.е. таких

функций, которые для всех значений параметров uj,2 , uj,3 , …, uj, т при-

нимают в точности соответствующие значения показателя yi , i =1, 2, …,

п. Вместе с тем для всех других значений параметров, отсутствующих в

результатах наблюдений, значения показателя могут принимать любые

значения. Понятно, что такие функции не соответствуют действительной

связи между параметрами и показателем

В целях выбора функциональной связи заранее выдвигают гипотезу

о том, к какому классу может принадлежать функция f, а затем подбирают

«лучшую» функцию в этом классе. Выбранный класс функций должен об-

ладать некоторой «гладкостью», т.е. «небольшие» изменения значений ар-

гументов должны вызывать «небольшие» изменения значений функции.

Простым, удобным для практического применения и отвечающим

указанному условию является класс полиномиальных функций

Для такого класса задача выбора функции сводится к задаче выбора

значений коэффициентов a0 , aj , ajk , …, ajj , … . Однако универсальность

полиномиального представления обеспечивается только при возможности

неограниченного увеличения степени полинома, что не всегда допустимо

на практике, поэтому приходится применять и другие виды функций.

Частным случаем, широко применяемым на практике, является по-

лином первой степени, или уравнение линейной регрессии

Это уравнение в регрессионном анализе следует трактовать как век-

торное, ибо речь идет о матрице данных

Обычно стремятся обеспечить такое количество наблюдений, кото-

рое превышало бы количество оцениваемых коэффициентов модели. Для

линейной регрессии при n > т количество уравнений превышает количест-

во подлежащих определению коэффициентов полинома. Но и в этом слу-

Ходасевич Г. Б. Обработка экспериментальных данных на ЭВМ. – СПб.: Санкт-

Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-

Бруевича.

чае нельзя подобрать коэффициенты таким образом, чтобы ошибка в каж-

дом скалярном уравнении обращалась в ноль, так как к неизвестным отно-

сятся аj и ui , их количество n + т – 1, т.е. всегда больше количества урав-

нений п. Аналогичные рассуждения справедливы и для полиномов степе-

ни, выше первой

На наш взгляд, использование линейного уравнения регрессии при-

менительно к определению стоимости объекта недвижимости возможно

только в том случае, если объекты-аналоги расположены в одном ценовом

диапазоне (тогда и можно говорить о внутренней линейности нелинейной

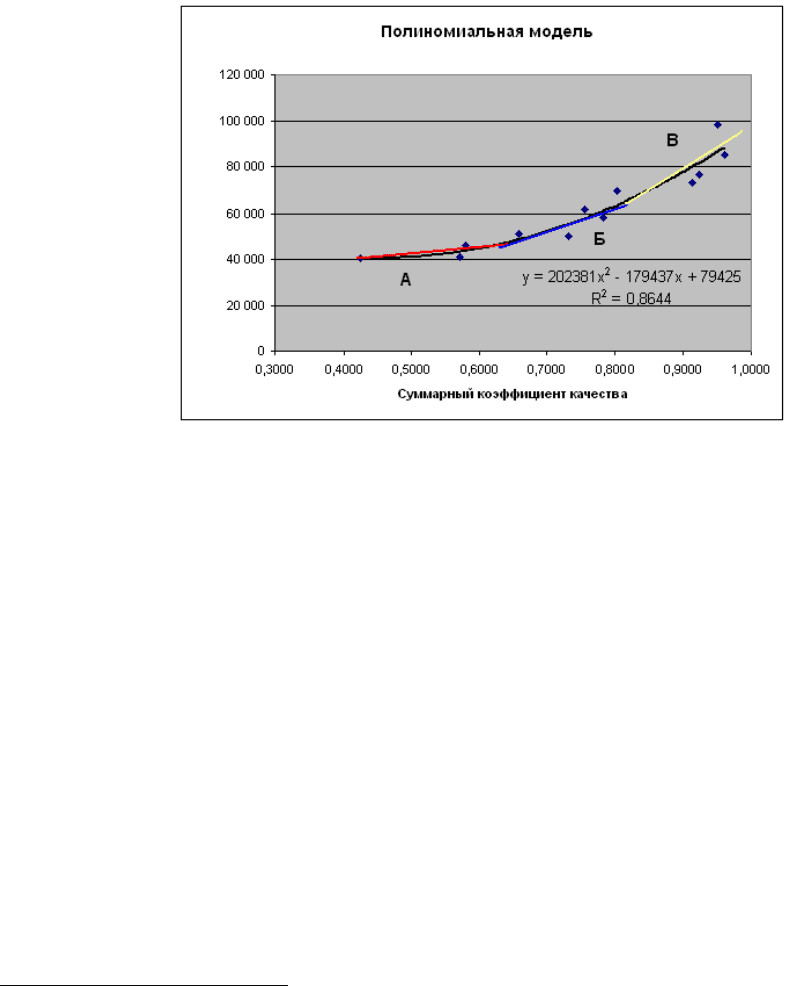
функции). На рис. 2 приведен пример ценовых диапазонов – А, Б, В.

Рис. 2

При расширении выборки объектов-аналогов: увеличении количест-

ва самих аналогов, расширении ценовых сегментов – можно рекомендо-

вать оценщикам к применению нелинейную модель регрессии (например,

полиномиальную или степенную).

Это можно объяснить тем, что, к примеру, увеличение на удельную

единицу качества объекта на отрезке Х{0.8;1.0} (рис. 2) не подразумевает

соразмерного увеличения удельной стоимости Y, т.к. зачастую ценообра-

зование высоких классов недвижимости носит не рыночный характер, а

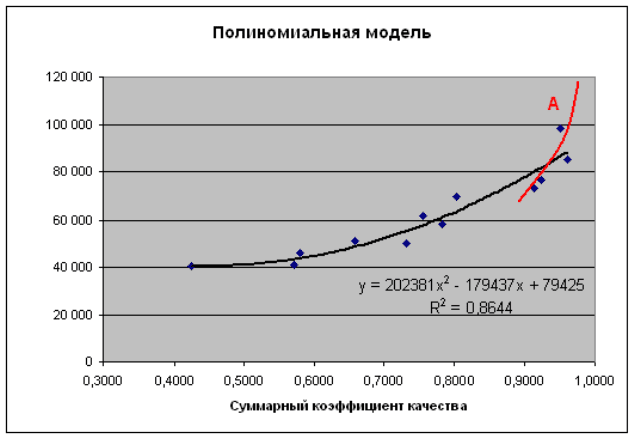
потребительский и зависит от желания продавца «снять сливки». Если

представить данную ситуацию графически, то получим тренд «A», изо-

браженный на рис. 3.

Также среди нелинейных функций, которые могут быть приведены к

линейному виду, в эконометрических исследованиях очень широко ис-

Ходасевич Г. Б. Обработка экспериментальных данных на ЭВМ. – СПб.: Санкт-

Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-

Бруевича.

пользуется степенная функция у = ах

bε

. Связано это с тем, что параметр b

в ней имеет четкое экономическое истолкование, т.е. он является коэффи-

циентом эластичности. Это означает, что величина коэффициента b по-

казывает, на сколько процентов изменится в среднем результат, если фак-

тор изменится на 1 %. По сути, распределение объектов на диаграмме рас-

сеивания представляет собой график предложения на микроуровне, кото-

рый также подвержен эластичности.

Рис. 3

В общем для выбора вида функциональной зависимости можно ре-

комендовать следующий подход:

 в пространстве параметров графически отображают точки со зна-

чениями показателя. При большом количестве параметров можно строить

точки применительно к каждому из них, получая двумерные распределе-

ния значений;

 по расположению точек и на основе анализа сущности взаимосвя-

зи показателя и параметров объекта делают заключение о примерном виде

регрессии или ее возможных вариантах;

 после расчета параметров оценивают качество аппроксимации,

т.е. оценивают степень близости расчетных и фактических значений;

 если расчетные и фактические значения близки во всей области

задания, то задачу регрессионного анализа можно считать решенной. В

противном случае можно попытаться выбрать другой вид полинома или

другую аналитическую функцию, например периодическую.

Хочется заметить, что в экономике, по существу, не бывает линей-

ных связей, это относится и к рынку недвижимости. Нелинейные модели

зачастую могут более корректно отобразить зависимость между ценообра-

зующими факторами от стоимости объекта, но построение таких моделей

и, главное, их проверка на значимость требуют от оценщика значительных

усилий и специфических знаний в области статистики и эконометрики.

М. М. Донской, аспирант

кафедры ценообразования

и оценочной деятельности СПбГУЭФ

Определение затрат на замещение биологических активов

При оценке аграрных предприятий значительный вклад в стоимость

основных средств данных предприятий вносят биологические активы.

Они, как и другие основные средства, по РБУ подлежат учету на 01, 07, 08

и 11 счетах.

Отраслевые особенности существенно влияют на организацию и

технологию производства и соответственно на построение бухгалтерского

учета. К таким специфическим объектам учета, которые не имеет ни одна

отрасль народного хозяйства, относятся животные на выращивании и от-

корме.

Молодняк животных и животные на откорме составляют особую

группу материальных оборотных средств. По своему экономическому со-

держанию животные на выращивании и откорме являются незавершен-

ным производством отрасли животноводства, потому что они постоянно

изменяют свою массу и соответственно стоимость. Эти изменения связа-

ны с расходами на содержание животных и их откорм до момента их реа-

лизации, забоя или перевода в основное стадо.

Согласно п. 1.2 «Инструкции по учету молодняка животных, птицы

и животных на откорме», утвержденной приказом Минсельхозпрода от

15.01.1997 г. № 7, не включают в состав молодняка животных, птиц и жи-

вотных на откорме поголовье основного стада продуктивного скота (коро-

вы и быки молочного и мясного направления; свиноматки без проверяе-

мых, боровы; конематки и жеребцы; овцематки, бараны-подростки и ва-

лухи, козы и козлы) и рабочий скот (кони, волы и т. п.).

Стоимость основного стада продуктивного и рабочего скота опреде-

ляется суммой стоимости его живого веса и продуктивных качеств. По-

следние характеризуются количеством продукции, которую можно полу-

чить от животных за год или за весь период хозяйственного использования.

Нетель – молодая беременная (до первого отела) самка крупного ро-

гатого скота

http://www.doclist.ru/slovar/netel.html

Лактация – секреция молока молочными железами, которая обычно

возникает в конце беременности

Потенциал продуктивности коровы определяется количеством и

функциональной активностью клеток молочной железы, способностью из

года в год проходить период отела и давать стабильный удой. Развитие

клеток молочной железы происходит в период беременности. С наступле-

нием лактации деление данных клеток замедляется и ко второй–четвертой

неделе вовсе прекращается. Одновременно с этим процессом происходит

резкий рост функциональной активности секреторных клеток и происхо-

дит быстрое увеличение удоев.

В качестве единицы сравнения была взята нетель красной степной

породы, находящаяся на 7 месяце беременности. Для окончательного

формирования продуктивных качеств и ввода данного объекта в стадо не-

обходимо кормить данную нетель еще 2 месяца, до того как она родит, да-

лее все затраты на раздой и кормление относятся на себестоимость про-

дукции. Суточная потребность в корме устанавливается на каждом пред-

приятии. Пример суточной потребности приведен в табл. 1.

Таблица 1

Суточная потребность нетели в корме

Наименование Потребность в корме в сутки, кг

Концентрированные 5,0

Шрот 2,0

Силос 30,0

Сено 5,0

Рандавит 0,2

Жом 10,0

Солома 2,0

Закупочные цены на сельскохозяйственную продукцию, заготавли-

ваемую перерабатывающими предприятиями в личных подсобных хозяй-

ствах, могут публиковаться как комитетом законодательного собрания то-

го региона, в котором находится объект оценки, так и самим перерабаты-

вающим предприятием.

Чтобы рассчитать стоимость продуктивных качеств, необходимо

стоимость нетели на дату ввода в эксплуатацию уменьшить на стоимость

живой массы нетели при сдаче ее на мясо и увеличить на стоимость двух-

месячной кормежки до отела.

http://vocabulary.ru/dictionary/480/word/%CB%C0%CA%D2%C0%D6%C8% DF

Основное различие между племенным и неплеменным скотом за-

ключается в периоде их использования. Так, после завершения пятого

лактационного периода у неплеменного скота и после завершения восьмо-

го лактационного периода у племенного скота резко падает показатель

удоя, и корову отправляют на убой, так как дальнейшее содержание ее в

стаде экономически невыгодно.

По данным исследования характеристик скота красной степной по-

роды по молочной продуктивности, опубликованного в «Вестнике Алтай-

ского государственного университета» № 3 (29) за 2007 год, молочная

продуктивность коров различается в зависимости от лактаций и представ-

лена в табл. 2.

Таблица 2

Молочная продуктивность коров в зависимости от возраста в лактациях

Лактация Количество прошедших лактаций Удой, кг

1 0 3 735,5

2 1 3 912,6

3 2 3 742,8

4 3 3 742,8

5 4 3 742,8

6 5 3 742,8

7 6 3 742,8

8 7 3 742,8

8 0,0

Суммарный удой за весь срок эксплуатации 30 104,9

При массовой оценке всего стада необходимо рассчитать средне-

взвешенные показатели удоя в зависимости от лактации по коровам, нахо-

дящимся в собственности колхоза.

Исходя из данных по племенному скоту и рассчитанных данных по

животным, находящимся на оцениваемом предприятии, можно рассчитать

коэффициент, который будет показывать, на сколько стоимость продук-

тивных качеств неплеменного скота ниже, чем стоимость продуктивных

качеств племенного скота.

Коэф = УНП / УП, где

УНП – суммарный удой за весь срок эксплуатации неплеменного скота,

УП – суммарный удой за весь срок эксплуатации племенного скота.

Также по этим показателям можно рассчитать процент износа продуктив-

ных качеств.

Наиболее подходящей моделью для определения коэффициента из-

носа продуктивных качеств является линейная модель, что объясняется

весьма малым снижением ежегодного удоя скота в продуктивный период

жизни.

Продуктивные качества коров определяются возможностью получе-

ния определенного количества молока.

По данным компании «Фирма Выбор», племенные нетели красной

степной породы при продаже имеют следующие технические данные:

 все животные имеют полный комплект документов: родословная, ве-

теринарное свидетельство и разрешение на вывоз;

 возраст: 18–30 месяцев на день поставки;

 вес: 450–550 кг в зависимости от возраста и стадии стельности на

момент отправки;

 стельность: 3–7 месяцев на момент отправки, подтвержденных по

результатам осмотра ветеринарным врачом.

Стоимость 1 килограмма живого веса коровы начинает снижаться

после того, как ее перевели в основное стадо. Корова остается в стаде до

тех пор, пока это экономически оправданно, как только удой у данной ко-

ровы падает, дальнейшая эксплуатация данной особи является убыточ-

ной – ее отправляют на убой, а стоимость становится равна стоимости за-

купки мяса.

Рассмотрен пример расчета полной стоимости замещения коровы:

 год рождения – 2004 г.;

 вес – 560 кг;

 состояние – продуктивная;

 оставшееся количество лактаций – 2.

1. Себестоимость 1 кг живого веса нетели для примера равна 36 руб.

2. Себестоимость живой массы нетели при сдаче его на мясо: 560 х 36 =

20 160 руб.

3. Стоимость затрат на двухмесячное кормление до отела:

Таблица 3

Пример затрат на кормление нетели

Наименование

Потребность

в корме в сутки, кг

Стоимость 1 кг

корма, руб.

Стоимость корма

в сутки, руб.

Концентрированные 5,0 4,5 22,5

Шрот 2,0 6,0 12,0

Силос 30,0 8,5 255,0

Сено 5,0 12,0 60,0

Рандавит 0,2 53,0 10,6

Жом 10,0 1,0 10,0

Солома 2,0 3,0 6,0

Итого в сутки 376,1

Итого за два месяца

22 566,0