Ваняшов А.Д., Кустиков Г.Г. Учебное пособие для курсового проектирования - Расчет и конструирование центробежных компрессорных машин

Подождите немного. Документ загружается.

Диффузоры первой и второй ступеней – лопаточные с предшествующим

им коротким безлопаточным участком. Лопаточные диффузоры обеих ступеней

также имеют одинаковые углы установки лопаток на входе

л3

=19°, на выходе

л4

= 35° и одинаковую ширину. Концевая ступень заканчивается кольцевой

сборной камерой прямоугольного поперечного сечения.

Корпус компрессора цилиндрической формы отлит из стали и имеет один

вертикальный монтажный разъем. Всасывающий и нагнетательный патрубки

приварены к корпусу. Относительно корпуса всасывающий патрубок располо-

жен радиально, а нагнетательный – тангенциально.

Проточная часть нагнетателя, включающая в себя ротор,

диффузоры, об-

ратный направляющий аппарат, внутренние диафрагмы объединены в единый

сборочный пакет, который устанавливается в корпус нагнетателя. Все статор-

ные элементы проточной части выполнены без горизонтального разъема.

Уравновешивание осевой силы, действующей на ротор, а следовательно, и

уменьшение удельного давления на рабочие колодки упорного вкладыша под-

шипника осуществляет думмис (разгрузочный поршень), насаженный

на вал с

натягом.

Опорные узлы ротора компрессора – подшипники скольжения. Опорные

подшипники, воспринимающие радиальную нагрузку, имеют пять стальных

колодок с баббитовой заливкой. Опорные подшипники расположены в корпусе

подшипников, которые крепятся непосредственно к корпусу и крышке корпуса

нагнетателя. Упорный подшипник расположен на стороне всасывания и имеет

отдельный корпус. Для смазки подшипниковых

узлов в компрессоре применя-

ется турбинное масло марки 22.

Внутренние уплотнения нагнетателя лабиринтного типа - ступенчатые.

Концевые уплотнения – контактные торцевые со смазкой трущейся пары. На-

гнетатель снабжен масляным баком, откуда масло под давлением подается к

концевым уплотнениям и опорным узлам. Масляный насос закреплен на крыш-

ке блока упорного узла и имеет привод от

вала нагнетателя через понижающий

редуктор.

Привод компрессора осуществляется от газотурбинной установки мощно-

стью 16 МВт. Частота вращения ротора – 5300 об/мин. Потребляемая мощ-

ность – 15,5 МВт.

В прил. 5 приведены примеры чертежей спроектированного центробежно-

го нагнетателя природного газа, в которые включены: 1) продольный разрез на-

гнетателя; 2) сборочный чертеж ротора; 3) сборочный чертеж рабочего колеса

первой ступени; 4)

детали, из которых состоит рабочее колесо – рабочий и по-

крывающий диски. На сборочные чертежи составлены спецификации. Чертежи

и конструкторская документация выполнены в соответствии с требованиями

[18, 19].

ЧАСТЬ II

КОНСТРУКТИВНЫЕ И ПРОЧНОСТНЫЕ РАСЧЕТЫ

ЭЛЕМЕНТОВ

ЦЕНТРОБЕЖНЫХ КОМПРЕССОРНЫХ МАШИН

Конструктивные и прочностные расчеты отдельных элементов

проектируемой центробежной компрессорной машины являются после

термогазодинамического расчета проточной части следующими разделами

курсового проектирования по дисциплинам «Теория, расчет и

конструирование компрессорных машин динамического действия» и

«Тепловые двигатели и нагнетатели».

Под конструктивными расчетами понимается определение тех размеров

элементов проточной части, которые не были рассчитаны в

ходе

термогазодинамического расчета (например, профилирование лопаток РК,

ЛД, ОНА; определение осевых габаритов проточной части, радиусов

закруглений дисков и диафрагм и т. д.), а также расчет и подбор других

элементов центробежного компрессора, не относящихся к проточной части

(например, определение размеров думмиса и упорного подшипника по

величине осевого усилия; подбор и расчет

размеров внутренних

лабиринтных и концевых уплотнений и т. д.).

Под прочностными расчетами понимается проверка соответствия

несущих нагрузку элементов центробежной компрессорной машины

условиям прочности и виброустойчивости. Задачей большинства этих

расчетов является определение фактических напряжений в материале деталей

и сравнение их с допускаемыми напряжениями (например, расчет дисков и

лопаток РК на прочность;

расчет заклепок РК и шпонок на срез; расчет вала

на прочность и нахождение критических частот вращения ротора).

В основу приведенных расчетов положены разработки известных в

турбокомпрессоростроении ученых - В.Ф. Риса, Г.А. Раера, В.Б. Шнеппа,

Г.С. Скубачевского, в смежных отраслях промышленности - М.Ф. Михалева,

Ю.А. Шиманского и др

При выполнении этого раздела курсового проекта студентам

рекомендуется использовать такие программные средства, как Pascal, Fortran,

Bаsiс, Microsoft Excel. Некоторые специальные задачи, не нашедшие

отражения в данном пособии, можно решать с помощью программного

пакета ANSIS.

Авторы выражают благодарность С.А. Девятову, кандидату технических

наук, доценту кафедры «Сопротивление материалов», за редактирование

главы «Прочностные расчеты».

1. Конструктивные расчеты элементов компрессора

К числу конструктивных расчетов турбокомпрессоров относятся

расчеты, связанные с определением размеров элементов проточной части в

меридиональной и радиальной плоскостях, не известные из

газодинамического расчета: построение профилей лопаток рабочих колес,

диффузоров и обратных направляющих аппаратов; выбор размеров

основных и покрывающих дисков, диафрагм; определение диаметров и

радиальной протяженности

лабиринтных уплотнений около основного и на

покрывающем дисках; расчет осевых усилий, действующих со стороны

потока на ротор компрессора; определение размеров думмиса и упорного

подшипника для компенсации осевых усилий.

1.1. Определение осевых усилий

Причиной возникновения осевых усилий является наличие перепада

давлений на дисках рабочих колес. Результирующее осевое усилие в

центробежных компрессорах

направлено в сторону всасывания. Следствием

неуравновешенных осевых усилий может быть сдвиг ротора относительно

корпусных деталей, что приводит к аварийной ситуации при работе

компрессора.

Снижение осевого усилия можно осуществить различными способами:

1) уменьшением степени реактивности рабочих колес; 2) повышением

диаметра уплотнений на стороне большего давления; 3) применением

компоновки рабочих колес с расположением всасывающих отверстий

навстречу друг другу или в противоположные стороны.

Для конструкций центробежных компрессоров с односторонним

всасыванием большая часть осевых усилий уравновешивается разгрузочным

поршнем (думмисом), расположенным за последним колесом на роторе, а

оставшаяся неуравновешенная часть осевых усилий воспринимается

упорным подшипником.

Расчету осевых усилий предшествует эскизная разработка продольного

разреза проточной части: вала с рабочими

колесами, диафрагм с

диффузорами и обратными направляющими аппаратами и элементов

корпуса. В результате определяются диаметры лабиринтных уплотнений

около основных дисков колес и диаметры уплотнений покрывающих дисков.

Осевую силу, действующую на рабочее колесо центробежной ступени,

можно представить в следующей форме [5]:

осп

FFFF

Σ 0

, (1.1)

где F

- осевая сила, действующая на рабочее колесо, при допущении

отсутствия протечек рабочего вещества через лабиринтные уплотнения, Н;

ос

- дополнительные осевые силы, приложенные к наружным

поверхностям покрывающего и основного дисков, Н.

Значение F

можно определить по уравнению, предложенному В. Ф.

Рисом [1, 2, 5, 8]:

()()

23244

DРРDDРDDF

ослпл

ослплослвт

−

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−−+−=

ρω

ππ

, (1.2)

где

об

n⋅

- угловая скорость вращения ротора, рад/с, (n

об

– частота

вращения ротора, об/мин); D

л.ос

и D

л.п

– диаметр расположения лабиринтных

уплотнений у основного и покрывающего дисков, м.

Диаметр лабиринтных уплотнений у покрывающего диска задается по

диаметру всасывающего отверстия колеса:

1,1 DD

пл

⋅

≈

Если достоверно значение диаметра под лабиринтные уплотнения у

основного диска не известно, можно предварительно принять D

л.ос

= D

вт

тогда формула (1.2) упростится.

Для концевой ступени, при выполнении поверочного расчета, когда

известен диаметр думмиса, следует принимать D

л.ос

= D

дум

Дополнительные силы

ос

возникают из-за изменения поля

скоростей и давлений в боковом зазоре между вращающимися дисками и

стенками статорных деталей при наличии протечек рабочего газа через

лабиринтные уплотнения. Для определения

ос

можно использовать

приближенные зависимости, предложенные В.Б. Шнеппом [14]. При течении

потока протечек сжимаемого газа от центра, что характерно для зазоров

между основным диском колеса и корпусом в промежуточных ступенях

компрессоров, имеющих ОНА (рис. 1.1 а):

⎥

⎦

⎤

⎢

⎣

⎡

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

= 1

ρω

, (1.3)

где

⋅

+= 3045,0

;

185,017,0

⋅+=

; q – коэффициент протечек.

При направлении протечек сжимаемого газа к центру, что характерно

для зазоров между покрывающими дисками колес и корпусом, а также между

основным диском и корпусом в ступенях концевого типа (рис.1.1 б):

()

qcb

⋅−⋅⋅

⋅⋅

ρω

, (1.4)

где

252776640

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

⎟

⎠

⎞

⎜

⎝

⎛

⋅=

лл

;

6,82258220

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

⎟

⎠

⎞

⎜

⎝

⎛

⋅=

лл

;

291,1575,125,1

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

⎟

⎠

⎞

⎜

⎝

⎛

⋅=

лл

При расчетах по формулам (1.3) и (1.4) дополнительных сил для

покрывающего

и основного

ос

дисков промежуточных и концевых

ступеней диаметры расположения лабиринтных уплотнений D

принимаются

соответственно: для покрывающего диска D

= D

л.п

(рис. 1.1), для основного

диска D

= D

л.ос.

(рис. 1.1 а, б).

При рассмотрении рабочего колеса в целом положительными

считаются силы, направленные в сторону всасывающего отверстия навстречу

втекающему в колесо потоку. В случае течения от центра в зазоре между

основным диском и корпусом, что характерно для ступеней промежуточного

типа, дополнительная сила

ос

, рассчитываемая по формуле (1.3),

получается отрицательной (

ос

). Это означает, что дополнительная сила

направлена к диску, т.е. в сторону всасывающего отверстия колеса, и в

формуле (1.1) ее следует прибавить к основной силе F

. В случае течения к

центру в зазоре между основным диском и корпусом, что характерно для

ступеней концевого типа, дополнительная сила

ос

, рассчитываемая по

формуле (1.4), получается положительной (

ос

). Это означает, что

дополнительная сила направлена от диска, т.е. в сторону нагнетания, и в

формуле (1.1) ее следует отнять от основной силы F

. Дополнительная сила

, рассчитываемая по формуле (1.4), всегда получается положительной

(

) и в формуле (1.1) суммируется с силой F

В уравнениях (1.3) и (1.4) аргументом является коэффициент протечки q,

который определяется перепадом давлений на выходе из колеса и давлением

за лабиринтным уплотнением.

При течении от центра значение q может быть найдено из уравнения [5]:

()

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−−+

⋅

=∆ 141,0125,000315,0

244.02

rлл

ρω

, (1.5)

где

РРР −=∆

′

, а при течении к центру [5]

()

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−+−−

⋅

=∆ 08,013,25,37,33700315,0

rлл

ψψ

ρω

, (1.6)

где

РРР −=∆

- для покрывающих дисков рабочих колес;

РРР −=∆

для рабочего диска последней ступени.

В формулах (1.5), (1.6) принято:

- коэффициент расхода через

лабиринтное уплотнение; s

- радиальный зазор в лабиринтном уплотнении,

м; z

- число гребней лабиринтного уплотнения (у покрывающего диска

= z

л.п

, у основного диска z

= z

л.ос

Уравнения (1.5) и (1.6) нелинейные. Решение их возможно методом

последовательных приближений или графоаналитическим способом. Но

уравнение (1.6) квадратное, и есть возможность его решить известными

математическими методами. В [13] эти уравнения решаются

графоаналитическим способом. Используя программные средства, например

Dл.п

Dвт

Dдум

Dл.ос.

Dвт

Dл.п

Dл.ос.

а) б)

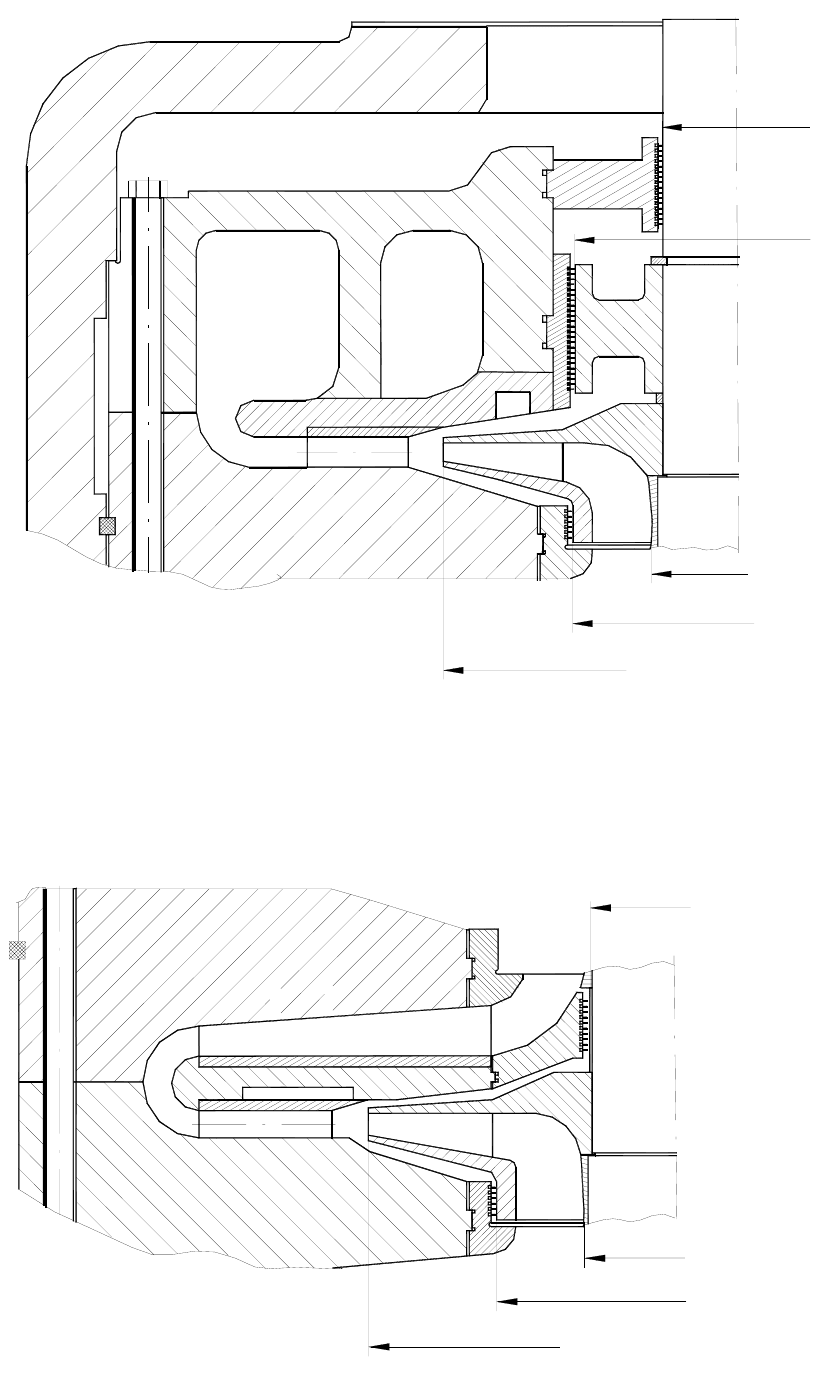
Рис. 1.1. Расчетные схемы ступеней к определению осевых усилий: а) промежуточная ступень;

б) концевая ступень

Microsoft Excel, данные уравнения можно решить методом последовательных

приближений. Порядок значений, которые может принимать коэффициент

протечек: q = 0,1

⋅10

-3

- 6⋅10

-3

Все входящие в данные уравнения геометрические размеры

принимаются по эскизу проточной части, а величины, характеризующие

термогазодинамические параметры потока, - в соответствии с

газодинамическим расчетом компрессора.

Для ступенчатых уплотнений

= 0,6-0,7; для гладких уплотнений

= 0,8-1,3 [14].

Число гребней лабиринтного уплотнения у покрывающего диска

л..п

= (3 – 6); у основного диска промежуточной ступени z

л..ос

= (6 – 10); для

концевой ступени на думмисе z

л..дум

= (12 – 30).

Величина радиального зазора выбирается по зависимости [2, 8, 9]:

10)4,02,0(

−

⋅⋅+= Ds

При расчете коэффициента протечек для основного диска концевой

ступени в формуле (1.6) вместо давления Р

подставляется давление

всасывания Р

(для газовых компрессоров) или давление Р

атм

(для

воздушных компрессоров).

Таким образом определяются осевые усилия для каждого рабочего

колеса компрессора. Затем находится общее осевое усилие, действующее на

ротор компрессора:

)()2()1(

)()(

...

iк

FFFFF

ΣΣΣ

ΣΣ

+++==

∑

. (1.7)

1.2. Определение размеров думмиса и упорного подшипника

В многоступенчатых центробежных компрессорах уменьшение осевого

усилия, воспринимаемого упорным подшипником, во избежание

значительных механических потерь и сокращения габаритных размеров

подшипника обеспечивается применением думмиса (разгрузочного поршня).

Прежде чем рассчитывать думмис, целесообразно подобрать упорный

подшипник (рис. 1.2) и оценить осевое усилие, которое он может воспринять.

Осевое усилие, воспринимаемое упорным подшипником, Н:

упкупупудуп

zblРF

⋅

, (1.8)

где b

уп

, l

уп

– соответственно радиальный и средний окружной размеры

упорных колодок; z

к.уп

– число колодок (обычно z

к.уп

=6-12), Р

уд

– удельное

давление масла на колодку, МПа.

Величиной удельного давления можно задаться:

)2,30,3()5,10,1(

−

уд

МПа.

Радиальный размер колодок упорного подшипника, м:

RRb

уп

−

lуп

lр.уп

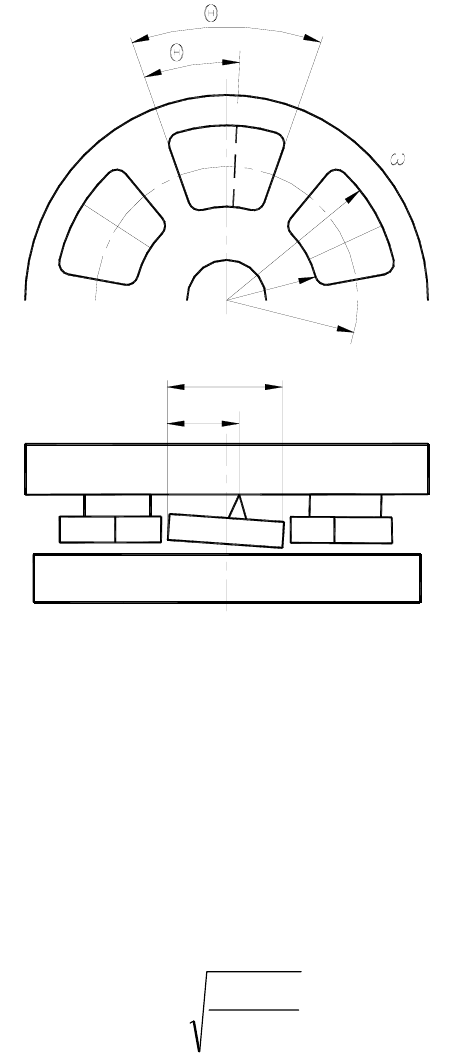
Рис. 1.2. Расчетная схема упорного подшипника

где R

и R

– радиусы наружной и внутренней поверхностей колодок (рис.

1.2), принимаемые конструктивно.

Можно ориентировочно принять

7,0 Rb

уп

⋅

≈

Радиус внутренней поверхности можно ориентировочно принять на

основании рассчитанного диаметра опорной поверхности вала [13]:

][

кр

τω

⋅

где N

– мощность на валу компрессора, МВт; [

кр

] - допускаемое

напряжение кручения для выбранной марки стали вала, МПа;

– угловая

скорость вращения ротора, рад/с,

1 ш

dR ≈

Средний окружной размер упорных колодок, м:

⋅

сруп

где

)(5,0

RRR

ср

+⋅=

;

- угол сектора, охватываемый колодкой, рад.

Угол сектора колодки можно принимать

= 30-35° (0,5-0,6 рад).

Максимальное повышение температуры масла в подшипнике,

°С [14]:

[

]

удупр

Рlet

ср

⋅−⋅−⋅⋅=∆

⋅

)5,0(8,2114

0015,0

max.

, (1.9)

где

срср

RU ⋅=

- окружная скорость центра упорного подшипника, м/с;

угловая скорость вращения ротора, рад/с;

упр

- относительное расстояние до

опорного ребра подушки (рис. 1.2); Р

уд

подставляется в (1.9), МПа.

575,05,0

−==

упупрупр

lll

Максимальная температура масла,

°С:

max..max. мнмм

ttt

∆

где t

м.н

– температура масла при подаче в подшипник.

сркмнм

Utt

⋅

04,0

где t

м.к

– температура масла на сливе из подшипника.

При нормальной работе подшипников температура масла на сливе не

превышает 50-55

°С (максимально до 60-65 °С) [14].

Полученная максимальная температура масла в подшипнике не должна

превышать предельно допустимой температуры [t

м.max

]=120 °C, при которой

масло начинает оксидироваться:

][

max.max. мм

В случае невыполнения этого условия необходимо уменьшить удельное

давление масла на колодку подшипника.

Осевое усилие, которое должно быть воспринято думмисом, Н:

упдум

FFF

−

Давление перед думмисом, Па [5]:

[

]

)(2

)(.)(2

)(2)(2

1125,0

XXослXХXдум

DDUРР −−=

где Р

2(X)

, ρ

2(X)

– давление и плотность газа в сечении 2-2 последней ступени;

2(X)

, D

2(X)

, D

л.ос(X)

– окружная скорость, диаметр рабочего колеса последней

ступени и диаметр уплотнений за думмисом.

Давление за думмисом равно давлению всасывания компрессора, т.к.

полость за думмисом соединена с линией всасывания компрессора или

сообщена с атмосферой для воздушных компрессоров.

Диаметр уплотнений думмиса

()

ндумXосл

дум

Xослдум

PPD

−⋅

⋅

)(.

Протечки через думмис определяются по уравнению

думдумл

думндум

думrлдумпр

DsG

⋅

⋅−

⋅⋅=

)(

где ρ

дум

– плотность газа в полости перед думмисом:

)(2

думХ

дум

⋅