Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

10.2 Means and Variances in Two Independent Normal Populations 359

: σ

=σ

versus H

: σ

6=σ

The testing statistic is the ratio of sample variances, F

= s

, that has an F

distribution with n

−1 and n

−1 degrees of freedom when H

is true. The

decision can be made based on a p-value that is equal to

p = 2

min( fcdf(F, n1-1, n2-1), 1-fcdf(F, n1-1, n2-1) )

Remark. We note that the most popular method (recommended in many

texts) for calculating the p-value in two-sided testing uses either the expres-

sion

fcdf(F,n1-1,n2-1) or 2

(1-fcdf(F,n1-1,n2-1)), depending on whether

F<1 or F>1. Although this approach leads to a correct p-value most of the time,

it could lead to a p-value that exceeds 1 when the observed values of F are

close to 1. This is clearly wrong since the p-value is a probability. Exercise 10.4

describes such a case.

MATLAB has a built-in function,

vartest2, for testing the equality of two

normal variances.

Guided by the outcome of this test, either we assume that the population

variances are the same and for testing the equality of means use a t-statistic

with a pooled standard deviation and df

= n

−2 degrees of freedom, or we

use the t-test without making an assumption about the population variances

and the degrees of freedom determined by the Welch–Satterthwaite formula

in (10.2).

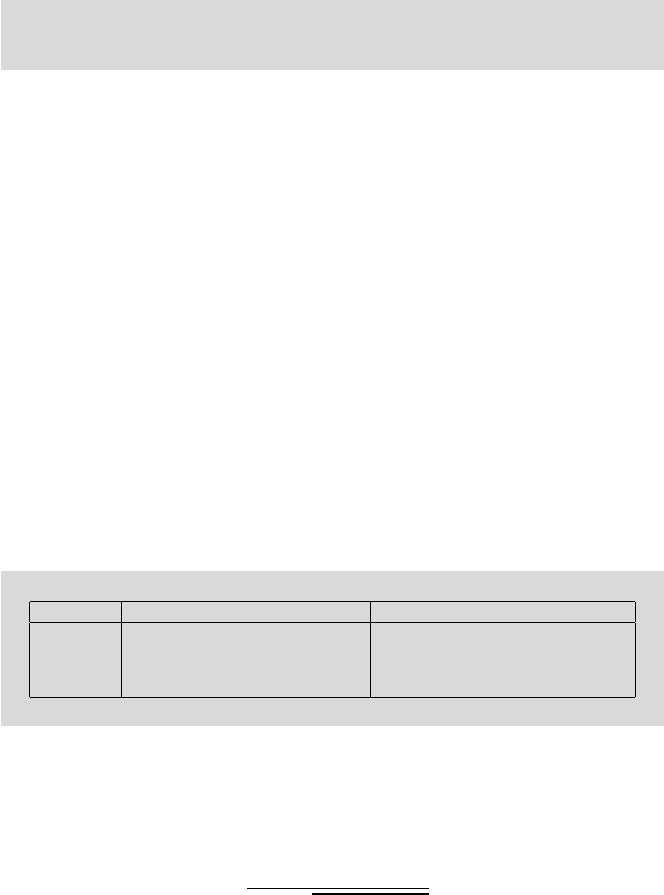
Next we summarize the test for both the one- and two-sided alternatives.

When H

: σ

= σ

and F = s

, the following table summarizes the test of

the equality of normal variances against the one- or two-sided alternatives.

Let df

= n

−1 and df

= n

−1.

Alternative α-level rejection region p-value

: σ

>σ

d f

,d f

,1−α

,∞) 1-fcdf(F,df1,df2)

: σ

6=σ

[0, F

d f

,d f

,α/2

] ∪[F

d f

,d f

,1−α/2

,∞)

min( fcdf(F,df1,df2),

(1-fcdf(F,df1,df2))

: σ

<σ

[0, F

d f

,d f

,α

] fcdf(F,df1,df2)

The F-test for testing the equality of variances assumes independent sam-

ples. Glass and Hopkins (1984, Sect. 13.9) gave a test statistic for testing the

equality of variances obtained from paired samples with a correlation coefﬁ-

cient r. The test statistic has a t distribution with n

−2 degrees of freedom,

−s

(1 −r

)/(n −2)

360 10 Two Samples

where s

, s

are the two sample variances, n is the number of pairs of obser-

vations, and r is the correlation between the two samples. This test is ﬁrst

discussed in Pitman (1939).

Example 10.2. In Example 10.1, the F-statistic for testing the equality of vari-

ances is 0.4444 and the hypothesis of equality of variances is not rejected at a

signiﬁcance level of

α =0.05; the p-value is 0.18.

n1 = 12; X1bar = 0.010; s1 = 0.004; %exposed

n2 = 15; X2bar = 0.006; s2 = 0.006; %non-exposed

Fstat = s1^2/s2^2

% Fstat = 0.4444

%The p-value is

pval = 2

min(fcdf(Fstat,n1-1,n2-1), 1-fcdf(Fstat,n1-1,n2-1))

% pval = 0.1825

Back to Testing Two Normal Means. Guided by the previous test we as-

sume that the population variances are the same, and for the original problem

of testing the means we use the t-statistic normalized by the pooled standard

deviation. The test statistic is

−X

1/n

+1/n

, where s

−1)s

+(n

−1)s

−2

and it is t-distributed with n

−2 degrees of freedom.

sp = sqrt( ((n1-1)

s1^2 + (n2-1)

s2^2 )/(n1 + n2 - 2))

% sp =0.0052

df= n1 + n2 - 2 %%df = 25

tstat = (X1bar - X2bar)/(sp

sqrt(1/n1 + 1/n2))

% tstat=1.9803

pvalue = 1 - tcdf(tstat, n1+n2-2)

% pvalue = 0.0294 approx 3%

The null hypothesis is rejected at the 5% level since 0.0294 <0.05.

Suppose that one wants to test H

using rejection regions. Since the al-

ternative hypothesis is one-sided and right-tailed, as

−µ

>0, the rejection

region is RR

=[t

−2,1−α

,∞).

tinv(1-0.05, df) %ans =1.7081

By rejection-region arguments, the hypothesis H

is rejected since t >

−2,1−α

, that is, the observed value of statistic t =1.9803 exceeds the crit-

ical value 1.7081.

10.2 Means and Variances in Two Independent Normal Populations 361

10.2.1 Conﬁdence Interval for the Difference of Means

Sometimes we might be interested in the (1 −α)100% conﬁdence interval for

the difference of the population means. Such conﬁdence intervals are easy to

obtain and they depend, as do the tests, on the assumption about population

variances. In general, the interval is

−X

−t

d f ,1−α/2

∗

, X

−X

d f ,1−α/2

∗

where for the equal variance case df

= n

−2 and s

∗

= s

1/n

+1/n

and for no assumption about the population variances case df is the Welch–

Satterthwaite value in (10.2) and s

∗

For the lead exposure example, the 95% conﬁdence interval for

−µ

[

−0.00016,0.0082]:

sp=sqrt(((n1-1)

s1^2 + (n2-1)

s2^2 )/(n1+n2-2)) % sp = 0.0052

df = n1 + n2 - 2 % df = 25

LB=X1bar-X2bar-tinv(0.975,df)

sqrt(1/n1+1/n2) % LB =-0.00016

UB=X1bar-X2bar+tinv(0.975,df)

sqrt(1/n1+1/n2) % UB = 0.0082

Note that this interval barely covers 0. A test for the equality of two

means against the two-sided alternative can be conducted by inspecting the

conﬁdence interval for their difference. For a two-sided test of level

α one

ﬁnds the (1

−α)100% conﬁdence interval, and if this interval contains 0, the

null hypothesis is not rejected. What may be concluded from the interval

[

−0.00016,0.0082] is the following. If instead of the one-sided alternative that

was found to be signiﬁcant at the 5% level (the p-value was about 3%) one car-

ried out the test against the two-sided alternative, the test of the same level

would fail to reject H

MATLAB’s toolbox “stats” has a built-in function, ttest2, that performs

two sample t-tests.

10.2.2 Power Analysis for Testing Two Means

In testing H

: µ

= µ

against the two-sided alternative H

: µ

6= µ

, for the

speciﬁc alternative

|µ

−µ

|=∆, an approximation of power is

−β =Φ







α/2

∆







1 −Φ







1−α/2

∆







. (10.3)

362 10 Two Samples

If the alternative is one-sided, say H

: µ

> µ

, then ∆ = µ

−µ

and the

power is

−β =1 −Φ







1−α

−

∆













∆







. (10.4)

The approximation is good if n

and n

are large, but for small to moderate

values of n

and n

it tends to overestimate the power.

Equations (10.3) and (10.4) are standardly used but are somewhat obsolete

since the noncentral t distribution (p. 217) needed for an exact power is readily

available.

We state the formulas in terms of MATLAB code:

In testing the equality of means in two normal populations using in-

dependent samples, H

: µ

= µ

, versus the one-sided alternative, the

group sample size for ﬁxed

α,β is

≥

2σ

|µ

−µ

1−α

1−β

)

where

is the common population variance. If the alternative is two-

sided, then z

1−α

is replaced by z

1−α/2

. In that case, the sample size is

approximate.

It is assumed that the group sample sizes are equal, i.e., that the total

sample size is N

=2n. If the variances are not the same, then

≥

+σ

|µ

−µ

1−α

1−β

)

1 - nctcdf(tinv(1-alpha/2,n1+n2-2), ...

n1+n2-2,Delta/(sp

sqrt(1/n1+1/n2)))...

+ nctcdf(tinv(alpha/2,n1+n2-2), ...

n1+n2-2,Delta/(sp

sqrt(1/n1+1/n2)))

For the one-sided alternative H

: µ

>µ

the code is

1 - nctcdf(tinv(1-alpha,n1+n2-2), ...

n1+n2-2,Delta/(sp

sqrt(1/n1+1/n2)))

10.2 Means and Variances in Two Independent Normal Populations 363

In the context of Example 10.1 let us ﬁnd the power of the test against the

alternative H

: µ

−µ

=0.005.

The power for a one-sided

α-level test against the alternative H

: µ

−µ

0.005(=∆) is given in (10.4). The normal approximation is used and s

and s

are plugged into the place of σ

and σ

power = 1-normcdf(norminv(1-0.05)-0.005/sqrt(s1^2/n1+s2^2/n2) )

%power= 0.8271

power = normcdf(norminv(0.05)+0.005/sqrt(s1^2/n1+s2^2/n2) )

%power= 0.8271

Thus the power is about 83%. This is an approximation and normal ap-

proximation tends to overestimate the power. The exact power is about 81%,

power=1-nctcdf(tinv(1-0.05,n1+n2-2),...

n1+n2-2,0.005/sqrt(s1^2/n1+s2^2/n2))

%power = 0.8084

We plan to design a future experiment to test the same phenomenon. When

data are collected and analyzed, we would like for the

α =5% test to achieve a

power of 1

−β =90% against the speciﬁc alternative H

: µ

−µ

=0.005. What

sample size will be necessary? Since determining the sample size to meet a

preassigned power and precision is prospective in nature, we assume that the

previous data were obtained in a pilot study and that

and σ

are “known”

and equal to the observed s

and s

. The sample size formula is

(σ

+σ

)(z

1−α

1−β

)

∆

which in MATLAB gives

ssize = (s1^2 + s2^2)

(norminv(0.95)+norminv(0.9))^2/(0.005^2)

% ssize = 17.8128 approx 18 each

The number of children is 18 per group if one wishes for the sample sizes

to be the same, n

= n

. In the following section we discuss the design with

= k × n

, for some k. Such designs can be justiﬁed by different costs of

sampling, where the meaning of “cost” may be more general than only the

ﬁnancial one.

10.2.3 More Complex Two-Sample Designs

Suppose that we are interested in testing the equality of normal population

means when the underlying variances in the two populations are

and σ

and not necessarily equal. Also assume that the desired proportion of sample

364 10 Two Samples

sizes to be determined is k = n

, that is, n

= k×n

. This proportion may be

dictated by the cost of sampling or by the abundance of the populations. When

equal group samples are desired, then k

=1,

(σ

+σ

/k)(z

1−α/2

1−β

)

|µ

−µ

, n

= k ×n

. (10.5)

As before,

, µ

, σ

, and σ

are unknown, and in the absence of any data,

one can express

|µ

−µ

in units of σ

+σ

/k to elicit the effect size, d

However, if preliminary or historic samples are available, then

, µ

, σ

and

can be estimated by X

, X

, s

, and s

, respectively, and plugged into

formula (10.6).

Example 10.3. Two Amanitas. Suppose that two independent samples of

= 12 and n = 15 spores of A. pantherina (“Panther”) and A. rubescens

(“Blusher”), respectively, are only a pilot study. It was found that the means

are

=6.3 and X

=7.5 with standard deviations of s

=2.12 and s

=1.94.

All measures are in

µm. Suppose that Blushers are twice as common as Pan-

thers.

Determine the sample sizes for future study that will ﬁnd the difference

obtained in the preliminary samples to be signiﬁcant at the level

α = 0.05

with a power of 1

−β =0.90.

Here, based on the abundance of mushrooms, 2n

= n

and k = 2. Substi-

tuting

, X

, s

, and s

into (10.6), one gets

(2.12

+1.94

/2)(z

0.975

0.9

)

|6.3 −7.5|

=46.5260 ≈47.

Here, the effect size was

|6.3 − 7.5|/

2.12

+1.94

/2 = 0.4752, which corre-

sponds to d

=0.4752

The “plug-in” principle applied in the above example is controversial. Pro-

ponents argue that in the absence of any information on

, µ

, σ

, and σ

, the

most “natural” procedure is to use their MLEs,

, X

, s

, and s

. Opponents

say that one is looking for a sample size that will ﬁnd the pilot difference to

be signiﬁcant at a level

α with a preassigned power. They further argue that,

due to routinely small sample sizes in pilot studies, the estimators for popula-

tion means and variances can be quite unreliable. This unreliability is further

compounded by taking the ratios and powers in calculating the sample size.

Remark. Cochran and Cox (1957) proposed a method of testing two normal

means with unequal variances according to which the rejection region is based

on a linear combination of t quantiles,

10.2 Means and Variances in Two Independent Normal Populations 365

1−α

−1,1−α

+(s

−1,1−α

for one-sided alternatives. For two-sided alternative 1

−α is replaced by 1−α/2.

This test is conservative, with the achieved level of signiﬁcance smaller than

the stated

α.

10.2.4 Bayesian Test of Two Normal Means

Bayesian testing of two means simply analyzes the posterior distribution of

the means difference, given the priors and the data. We will illustrate a

Bayesian approach for a simple noninformative prior structure.

Let X

, X

,... , X

1,n

and X

, X

,... , X

2,n

be samples from normal

N (µ

,σ

) and N (µ

,σ

) distributions, respectively. We are interested in the

posterior distribution of

θ = µ

−µ

when σ

= σ

. If the priors on µ

and µ

are ﬂat, π(µ

) = π(µ

) = 1, and the prior on the common σ

is nonin-

formative,

π(σ

) = 1/σ

, then the posterior of θ, after integrating out σ

, is a t

distribution. That is to say, if

and X

are the sample means and s

is the

pooled standard deviation, then

θ −(X

−X

)

1/n

+1/n

(10.6)

has a t distribution with n

−2 degrees of freedom (Box and Tiao, 1992,

p. 103). Compare (10.6) with the distribution in (10.1). Although the two distri-

butions coincide, they are conceptually different; (10.1) is the sampling distri-

bution for the difference of sample means, while (10.6) gives the distribution

for the difference of parameters.

In this case, the results of Bayesian inference coincide with frequentist re-

sults on the estimation of

θ, the conﬁdence/credible intervals for θ and testing,

as is usually the case when the priors are noninformative.

When

and σ

are not assumed equal and each has its own noninfor-

mative prior, ﬁnding the posterior in the previous model coincides with the

Behrens–Fisher problem and the posterior is usually approximated (Patil’s

approximation, Box and Tiao, 1992, p. 107; Lee, 2004, p. 145).

When MCMC and WinBUGS are used in testing two normal means, we

may entertain more ﬂexible models. The testing becomes quite straightfor-

ward. Next, we provide an example.

Example 10.4. Microdamage in Bones. Bone is a hierarchical composite

material that provides our bodies with mechanical support and facilitates

mobility, among other functions. Figure 10.1 shows the structure of bone

tubecules. Damage in bone, in the form of microcracks, occurs naturally dur-

ing daily physiological loading. The normal bone remodeling process repairs

366 10 Two Samples

this microdamage, restoring, if not improving, biomechanical properties. Nu-

merous studies have shown that microdamage accumulates as we age due to

impaired bone remodeling. This accumulation contributes to a reduction in

bone biomechanical properties such as strength and stiffness by disrupting

the local tissue matrix.

In order to better understand the role of microdamage in bone tissue ma-

trix properties as we age, a study was conducted in the lab of Dr. Robert Guld-

berg at Georgia Institute of Technology. The interest was in changes in micro-

damage progression in human bone between young and old female donors.

Fig. 10.1 Bone tubecules.

The data showing the score of normalized damage events are shown in the

table below. There were n

=13 donors classiﬁed as young (≤45 years old and

= 17 classiﬁed as old (>45 years old). To calculate the microdamage pro-

gression score, the counts of damage events (extensions, surface originations,

widenings, and combinations) are normalized to the bone area and summed

up.

Young Old

0.790 1.264 1.374 1.327

0.944 1.410 0.601 1.325

0.958 1.160 1.029 2.012

1.011 0.179 1.264 1.026

0.714 1.183 1.130

0.256 1.856 0.605

0.406 1.899 0.870

0.135 0.486 0.820

0.316 0.813

Assuming that the microdamage scores are normally distributed, test the

hypothesis of equality of population means (young and old) against the one-

sided alternative.

10.3 Testing the Equality of Normal Means When Samples Are Paired 367

#microdamage.odc

model{

for (i in 1:n){

score[i] ~ dnorm(mu[age[i]], prec[age[i]])

}

mu[1] ~ dnorm(0, 0.00001)

mu[2] ~ dnorm(0, 0.00001)

prec[1] ~ dgamma(0.001, 0.001)

prec[2] ~ dgamma(0.001, 0.001)

d <- mu[1] - mu[2]

r <- prec[1]/prec[2]

ph1 <- step(-d) #ph1=1 if d < 0

ph0 <- 1-ph1

}

DATA

list(n=30,score=c(0.790, 0.944, 0.958, 1.011, 0.714, 0.256, 0.406,

0.135, 0.316, 0.179, 1.264, 1.410, 1.160, 1.374,

0.601, 1.029, 1.264, 1.183, 1.856, 1.899, 0.486,

0.813, 0.820, 1.327, 1.325, 2.012, 1.026, 1.130,

0.605, 0.870),

age = c(1,1,1,1,1,1,1,1,1,1,1,1,1,

2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2))

INITS

list( mu = c(1,1), prec=c(1,1))

mean sd MC error val2.5pc median val97.5pc start sample

d –0.4194 0.1771 5.438E-4 –0.7688 –0.4192 –0.071 1001 100000

mu[1] 0.7339 0.1326 4.099E-4 0.4703 0.7338 0.9968 1001 100000

mu[2] 1.153 0.118 3.685E-4 0.9188 1.153 1.389 1001 100000

ph0 0.01011 0.1 3.112E-4 0.0 0.0 0.0 1001 100000

ph1 0.9899 0.1 3.112E-4 1.0 1.0 1.0 1001 100000

r 1.244 0.7517 0.002553 0.3456 1.071 3.155 1001 100000

The posterior probability of H

is 0.9899, thus H

is rejected. Note that

the credible interval for the difference d is all negative, suggesting that the

two-sided test would be signiﬁcant (in Bayesian terms). The ratio of precisions

(and variances) r has a credible set that contains 1; thus the variances could

be assumed equal. This assumption has no bearing on the Bayesian procedure

(unlike the classical approach).

10.3 Testing the Equality of Normal Means When

Samples Are Paired

When comparing two treatments it is desirable that the experimental units be

as alike as possible so that the difference in responses can be attributed chieﬂy

368 10 Two Samples

to the treatment. If many relevant factors (age, gender, body mass index, pres-

ence of risk factors, and so on) vary in an uncontrolled manner, a large portion

of variability in the response can be attributed to these factors rather than the

treatments.

The concept of pairing, matching, or blocking is critical to eliminate nui-

sance variability and obtain better experimental designs. Consider a sample

consisting of paired elements, so that every element from population 1 has

its match from population 2. A sample from population 1, X

, X

,... , X

1,n

, is

thus paired with a sample from population 2, X

, X

,... , X

2,n

, so that a pair

, X

) represents the ith observation. Usually, observations in a pair are

taken on the same subject (pretest–posttest, placebo–treatment) or on depen-

dent subjects (brother–sister, two subjects with matching demographic char-

acteristics, etc.). The examples are numerous, but most applications involve

subjects with measurements taken at two different time points, during two

different treatments, and so on. Sometimes this matching is called “blocking.”

It is usually assumed that the samples come from normal populations

with possibly different means

and µ

(subject to test) and with unknown

variances

and σ

. As linear combinations of normals, the differences d

−X

are also normal,

∼N (µ

−µ

,σ

+σ

−2 ·σ

where

is the covariance, E

[

−EX

)(X

−EX

)

]

. Deﬁne

, (10.7)

where

d is an average of the differences d

and s

is the sample standard

deviation of the differences. Here, the sample size n relates to the number of

pairs and not the total number of observations, which is 2n.

Note that one can express s

−2s

, where s

is the estimator

of covariance between the samples:

n −1

i=1

−X

)(X

−X

For example, in MATLAB,

x1 = [2 4 5 6 5 7 8];

x2 = [6 8 6 5 3 4 2];

d = x1 - x2;

sd = std(d)

%ans =3.6904

co=cov(x1, x2)

%co = 3.9048 -2.7857

% -2.7857 4.1429