Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support
Подождите немного. Документ загружается.

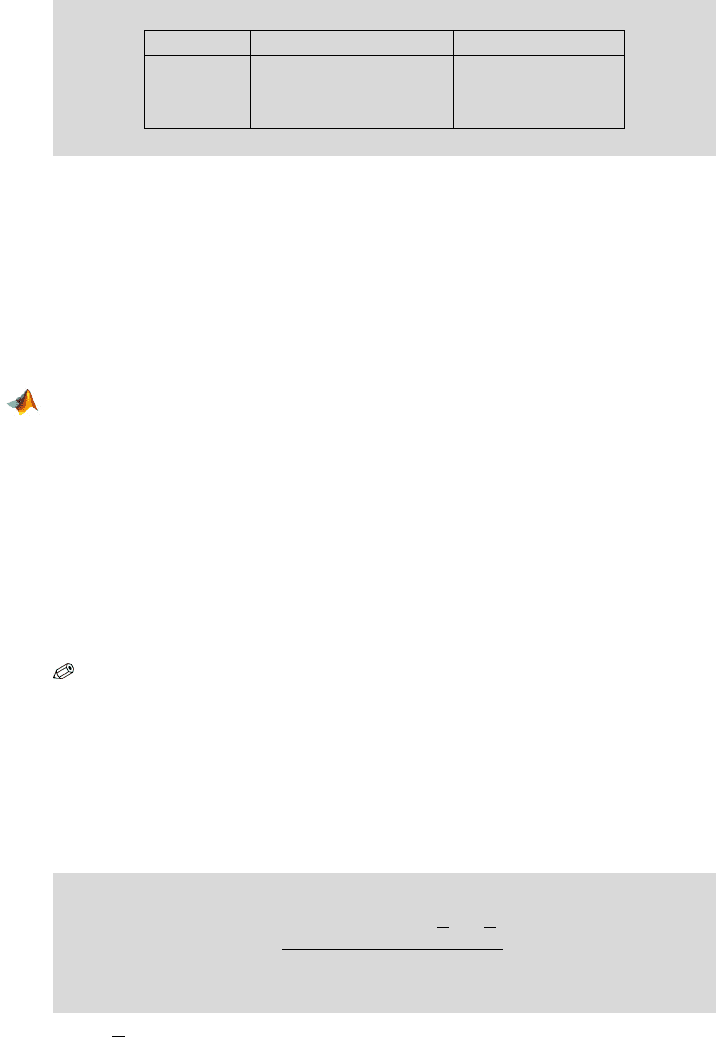
10.5 Comparing Two Proportions 379
Alternative α-level rejection region p-value
H
1
: p
1
> p
2
[z
1−α
,∞) 1-normcdf(z)
H
1
: p
1
6= p
2
(−∞, z
α/2
] ∪[z
1−α/2
,∞) 2
*
normcdf(-abs(z))
H
1
: p
1
< p
2
(−∞, z
α
] normcdf(z)
Example 10.10. Vasectomies and Prostate Cancer. Several studies have
been conducted to analyze the relationship between vasectomy and prostate
cancer. The study by Giovannucci et al. (1993) states that of 21,300 men who
had not had a vasectomy, 69 were found to have prostate cancer, while of
22,000 men who had a vasectomy, 113 were found to have prostate cancer.
Formulate hypotheses and perform a test at the 1% level.
x1=69; x2 = 113; n1 = 21300; n2 = 22000;
p1hat = x1/n1; p2hat = x2/n2; phat = (x1 + x2)/(n1 + n2);
z=(p1hat - p2hat)/(sqrt(phat
*
(1-phat))
*
sqrt(1/n1 + 1/n2))
% z = -3.0502
pval = normcdf(-3.0502)
% pval = 0.0011
We tested H
0
: p
1
= p
2
versus H
1
: p
1
< p
2
, where p
1
is the proportion
of subjects with prostate cancer in the population of all subjects who had a
vasectomy, while p
2
is the proportion of subjects with prostate cancer in the
population of all subjects who did not have a vasectomy. Since the p-value was
0.0011, we concluded that vasectomy is a significant risk factor for prostate
cancer.
10.5.1 The Sample Size
The sample size required for a two-sided α-level test to detect the difference
δ =|p
1
− p
2
|, with a power of 1 −β, is
n ≥
(z
1−α/2
+z
1−β
)
2
×2p(1 − p)
δ
2
,
where
p = (p
1
+ p
2
)/2. The sample size n is for each group, so that the total
number of observations is 2n. If the alternative is one-sided, z
1−α/2
is replaced
380 10 Two Samples
by z
1−α
. This formula requires some preliminary knowledge about p. In the
absence of any information about the proportions, the most conservative choice
for
p is 1/2.
Example 10.11. An investigator believes that a control group would have an
annual event rate of 30% and that the treatment would reduce this rate to
20%. She wants to design a study to be one-sided with a significance level of
α =0.05 and a power of 1 −β =0.85. The necessary sample size per group is
n = 2
*
(norminv(1-0.05)+norminv(1-0.15))^2
*
0.25
*
(1-0.25)/0.1^2
% n = 269.5988
This number is rounded to 270, so that the total sample size is 2 ×270 =540.
More precise sample sizes are
n
0
=
³
z
1−α/2
p
2p(1− p) +z
1−β
p
p
1
(1 − p
1
) + p
2
(1 − p
2
)
´
2
δ
2
,
with z
1−α/2
replaced by z
1−α
for the one-sided alternative.
Casagrande et al. (1978) propose a correction to n
0
as
n
00
= n
0
/4 ×
Ã
1 +
s
1 +
4
n
0
δ
!
2
,
while Fleiss et al. (1980) suggest n
000
= n
0
+
2
δ
.
In all three scenarios, however, preliminary knowledge about p
1
and p
2
is
needed.
%Sample Size for Each Group:
n1 = (norminv(1-0.05)
*
sqrt(2
*
0.25
*
0.75)+ ...
norminv(1-0.15)
*
sqrt(0.3
*
0.7+0.2
*
0.8))^2/0.1^2
%n1 = 268.2064
%Casagrande et al. 1978
n2 = n1/4
*
(1 + sqrt(1 + 4/(n1
*
0.1)))^2
%n2 =287.8590
%Fleiss et al. 1980
n3 = n1 + 2/0.1
%n3 = 288.2064
The outputs n
0
, n
00
, and n
000
are rounded to 267, 288, and 289, so that the
total sample sizes are 534, 576, and 578, respectively.
10.6 Risks: Differences, Ratios, and Odds Ratios
In epidemiological and population disease studies it is often the case that the
findings are summarized as a table

10.6 Risks: Differences, Ratios, and Odds Ratios 381
Disease present (D) No disease present (C) Total
Exposed (E) a b n
1
=a +b
Nonexposed (E
c
) c d n
2
= c +d
Total m
1
=a +c m
2
= b +d n = a +b +c +d
In clinical trial studies, the risk factor status (E/E
c
) can be replaced by a treat-
ment/control or new treatment/old treatment, while the disease status (D/D
c
)
can be replaced by a improvement/nonimprovement.
Remark. In the context of epidemiology, the studies leading to tabulated
data can be prospective and retrospective. In a prospective study, a group of
n disease-free individuals is identified and followed over a period of time. At
the end of the study, the group, typically called the cohort, is assessed and
tabulated with respect to disease development and exposure to the risk factor
of interest.
In a retrospective study, groups of m
1
individuals with the disease (cases)
and m
2
disease-free individuals (controls) are identified and their prior expo-
sure histories are assessed. In this case, the table summarizes the numbers of
exposure to the risk factor under consideration among the cases and controls.
10.6.1 Risk Differences
Let p
1
and p
2
be the population risks of a disease for exposed and nonex-
posed (control) subjects. These are probabilities that the subjects will develop
the disease during the fixed interval of time for the two groups, exposed and
nonexposed.
Let
ˆ
p
1
= a/n
1
be an estimator of the risk of a disease for exposed subjects
and
ˆ
p
2
= c/n
2
be an estimator of the risk of that disease for control subjects.
The (1
−α)100% confidence interval for the risk difference coincides with
the confidence interval for the difference of proportions from p. 378:
ˆ
p
1
−
ˆ
p
2
± z
1−α/2
s
ˆ
p
1
(1 −
ˆ
p
1
)
n
1
+
ˆ
p
2
(1 −
ˆ
p
2
)
n
2
.
Sometimes, better precision is achieved by a confidence interval with con-
tinuity corrections:
382 10 Two Samples
"
ˆ
p
1
−
ˆ
p
2
±(1/(2n
1
) +1/(2n
2
)) −z
1−α/2
s
ˆ
p
1
(1 −
ˆ
p
1
)
n
1
+
ˆ
p
2
(1 −
ˆ
p
2
)
n
2
,
ˆ
p
1
−
ˆ
p
2
±(1/(2n
1
) +1/(2n
2
)) +z
1−α/2
s
ˆ
p
1
(1 −
ˆ
p
1
)
n
1
+
ˆ
p
2
(1 −
ˆ
p
2
)
n
2
#
,
where the sign of the correction factor 1/(2n
1
) +1/(2n
2
) is taken as “+” if
ˆ
p
1
−
ˆ
p
2
<0 and as “−” if
ˆ
p
1
−
ˆ
p
2
>0. The recommended sample sizes for the validity
of the interval should satisfy min
{n
1
p
1
(1 − p
1
), n
2
p
2
(1 − p
2
)} ≥ 10. For large
sample sizes, the difference between “continuity-corrected” and uncorrected
intervals is negligible.
10.6.2 Risk Ratio
The risk ratio in a population is the quantity R = p
1
/p
2
. It is estimated by
r
=
ˆ
p
1
/
ˆ
p
2
. The empirical distribution of r does not have a simple form, and,
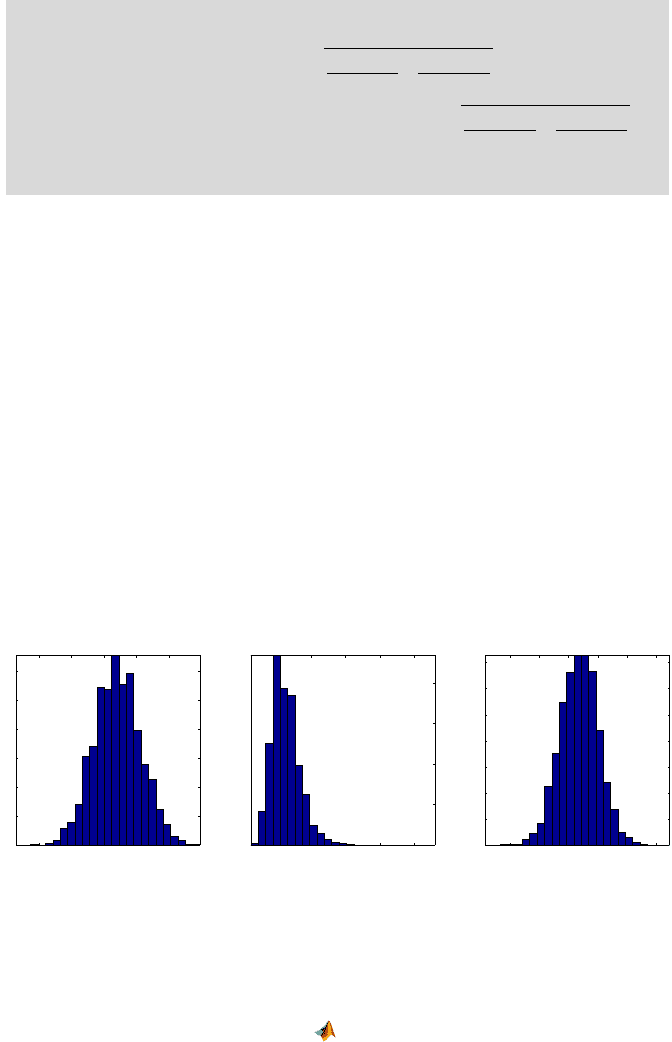
moreover, it is typically skewed (Fig. 10.3b). If the logarithm is taken, the risk
ratio is “symmetrized,” the log ratio is equivalent to the difference between
logarithms, and, given the independence of populations, the CLT applies. It is
evident in Fig. 10.3c that the log risk ratios are well approximated by a normal
distribution.
−0.2 −0.1 0 0.1 0.2
0
200
400
600
800
1000
1200
1 2 3 4 5
0
500
1000
1500
2000
−1 −0.5 0 0.5 1 1.5
0
200
400
600
800
1000
1200
1400
(a) (b) (c)
Fig. 10.3 Two samples of size 10,000 are generated from
B in(80,0.21) and B in(60, 0.25)
populations and risks
ˆ
p
1
and
ˆ
p
2
are estimated for each pair. The panels show histograms of
(a) risk differences, (b) risk ratios, and (c) log risk ratios.
The following MATLAB code ( simulrisks.m) simulates 10,000 pairs
from
B in(80,0.21) and B in(60, 0.25) populations representing exposed and

10.6 Risks: Differences, Ratios, and Odds Ratios 383
nonexposed subjects. From each pair risks are assessed and histograms of risk
differences, risk ratios, and log risk ratios are shown in Fig. 10.3a–c.
disexposed = binornd(60, 0.25, [1 10000]);
disnonexposed = binornd(80, 0.21, [1 10000]);
p1s = disexposed/60; p2s =disnonexposed/80;
figure; hist(p1s - p2s, 25)
figure; hist(p1s./p2s, 25)
figure; hist( log( p1s./p2s ), 25 )
10.6.3 Odds Ratios
For a particular proportion, p, the odds are defined as
p
1−p
. For two proportions
p
1
and p
2
, the odds ratio is defined as O =
p
1
/(1−p
1
)
p
2
/(1−p
2
)
, and its sample counterpart
is o
=
ˆ
p
1
/(1−
ˆ
p
1
)
ˆ
p
2
/(1−
ˆ
p
2
)
.
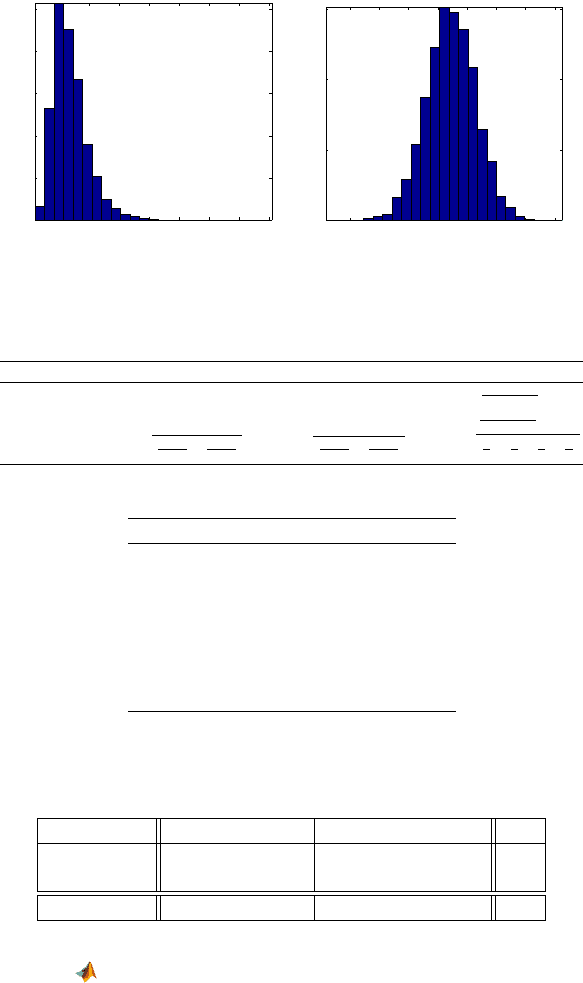
As evident in Fig. 10.4, the odds ratio is symmetrized by the log trans-
formation, and it is the log domain where the normal approximations are
used. The sample standard deviation for log o is s
log o
=
q
1
a
+
1
b
+
1
c
+
1
d
, and
the (1
−α)100% confidence interval for the log odds ratio is
"
log o −z
1−α/2
s
1
a
+
1
b
+
1
c
+
1
d
, log o
+z
1−α/2
s
1
a
+
1
b
+
1
c
+
1
d
#
.
Of course, the confidence interval for the odds ratio is obtained by taking
the exponents of the bounds:
"
exp
(
log o −z
1−α/2
s
1
a
+
1
b
+
1
c
+
1
d
)
, exp
(
log o +z
1−α/2
s
1
a
+
1
b
+
1
c
+
1
d
)#
.
Many authors argue that only odds ratios should be reported and used
because of their superior properties over risk differences and risk ratios (Ed-
wards, 1963; Mosteller, 1968). For small sample sizes replacing counts a, b, c,
and d by a
+1/2, b +1/2, c +1/2, and d +1/2 leads to a more stable inference.
384 10 Two Samples
1 2 3 4 5 6 7 8
0
500
1000
1500
2000
2500
−1.5 −1 −0.5 0 0.5 1 1.5 2
0
500
1000
1500
(a) (b)
Fig. 10.4 For the data leading to Fig. 10.3, the histograms of (a) odds ratios and (b) log odds
ratios are shown.
Risk difference Relative risk Odds ratio
Parameter D = p
1
− p
2
R = p
1
/p
2
O =
p
1
/(1−p
1
)
p
2
/(1−p
2
)
Estimator d =
ˆ
p
1
−
ˆ
p
2
r =
ˆ
p
1
/
ˆ
p
2
o =
ˆ
p
1
/(1−
ˆ
p
1
)
ˆ
p
2
/(1−
ˆ
p
2
)
St. deviation s
d
=
q
p
1
q
1
n
1
+
p
2
q
2
n
2
s
log r
=
q
q
1
n
1
p
1
+
q
2
n
2
p
2
s
log o
=
q
1
a
+
1
b
+
1
c
+
1
d
Interpretation of values for RR and OR are provided in the following table:
Value in Effect of exposure
[0,0.4) Strong benefit
[0.4,0.6) Moderate benefit
[0.6,0.9) Weak benefit
[0.9,1.1] No effect
(1.1,1.6] Weak hazard
(1.6,2.5] Moderate hazard
>2.5 Strong hazard
Example 10.12. Framingham Data. The table below gives the coronary
heart disease status after 18 years, by level of systolic blood pressure (SBP).
The levels of SBP
≥165 are considered as an exposure to a risk factor.
SBP (mmHg) Coronary disease No coronary disease Total
≥165 95 201 296
<165 173 894 1067
Total 268 1095 1363
Find 95% confidence intervals for the risk difference, risk ratio, and odds ratio.
The function
risk.m calculates confidence intervals for risk differences, risk
ratios, and odds ratios and will be used in this example.

10.6 Risks: Differences, Ratios, and Odds Ratios 385
function [rd rdl rdu rr rrl rru or orl oru] = risk(a, b, c, d, alpha)
%--------
% | Disease No disease Total
% --------------------------------------------------------
% Exposed | a b | n1
% Nonexposed | c d | n2
% --------------------------------------------------------
if nargin < 5
alpha=0.05;
end
%--------
n1 = a + b;
n2 = c + d;
hatp1 = a/n1; hatp2 = c/n2;
%-------risk difference (rd) and CI [rdl, rdu] ---------
rd = hatp1 - hatp2;
stdrd = sqrt(hatp1
*
(1-hatp1)/n1 + hatp2
*
(1- hatp2)/n2 );
rdl = rd - norminv(1-alpha/2)
*
stdrd;
rdu = rd + norminv(1-alpha/2)
*
stdrd;
%----------risk ratio (rr) and CI [rrl, rru] -----------
rr = hatp1/hatp2;
lrr = log(rr);
stdlrr = sqrt(b/(a
*
n1) + d/(c
*
n2));
lrrl = lrr - norminv(1-alpha/2)
*
stdlrr;
rrl = exp(lrrl);
lrru = lrr + norminv(1-alpha/2)
*
stdlrr;
rru = exp(lrru);
%---------odds ratio (or) and CI [orl, oru] ------------
or = ( hatp1/(1-hatp1) )/(hatp2/(1-hatp2))
lor = log(or);
stdlor = sqrt(1/a + 1/b + 1/c + 1/d);
lorl = lor - norminv(1-alpha/2)
*
stdlor;
orl = exp(lorl);
loru = lor + norminv(1-alpha/2)
*
stdlor;
oru = exp(loru);
The solution is:
[rd rdl rdu rr rrl rru or orl oru] = risk(95,201,173,894)
%rd = 0.1588
%[rdl, rdu] = [0.1012, 0.2164]
%rr = 1.9795
%[rrl, rru]= [1.5971, 2.4534]
%or = 2.4424
%[orl, oru] = [1.8215, 3.2750]
Example 10.13. Retrospective Analysis of Smoking Habits. This exam-
ple is adopted from Johnson and Albert (1999), who use data collected in a
386 10 Two Samples
study by Dorn (1954). A sample of 86 lung-cancer patients and a sample of
86 controls were questioned about their smoking habits. The two groups were
chosen to represent random samples from a subpopulation of lung-cancer pa-
tients and an otherwise similar population of cancer-free individuals. Of the
cancer patients, 83 out of 86 were smokers; among the control group, 72 out
of 86 were smokers. The scientific question of interest was to assess the dif-
ference between the smoking habits in the two groups. Uniform priors on the
population proportions were used as a noninformative choice.
model{
for(i in 1:2){
r[i] ~ dbin(p[i],n[i])
p[i] ~ dunif(0,1)
}
RD <- p[1] - p[2]
RD.gt0 <- step(RD)
RR <- p[1]/p[2]
RR.gt1 <- step(RR - 1)
OR <- (p[1]/(1-p[1]))/(p[2]/(1-p[2]))
OR.gt1 <- step(OR - 1)
}
DATA
list(r=c(83,72),n=c(86,86))
INITS
#Generate Inits
mean sd MC error val2.5pc median val97.5pc start sample
OR 5.818 4.556 0.01398 1.556 4.613 17.29 1001 100000
OR.gt1 0.9978 0.04675 1.469E-4 1.0 1.0 1.0 1001 100000
RD 0.125 0.0455 1.478E-4 0.0385 0.1237 0.2179 1001 100000
RD.gt0 0.9978 0.04675 1.469E-4 1.0 1.0 1.0 1001 100000
RR 1.153 0.06276 2.038E-4 1.044 1.148 1.291 1001 100000
RR.gt1 0.9978 0.04675 1.469E-4 1.0 1.0 1.0 1001 100000
p[1] 0.9546 0.02209 7.06E-5 0.9022 0.958 0.9873 1001 100000
p[2] 0.8296 0.03991 1.26E-4 0.7444 0.8322 0.9002 1001 100000
Note that 95% credible sets for the risk ratio and odds ratio are above 1,
and that the set for the risk difference does not contain 0. By all three mea-
sures the proportion of smokers among subjects with cancer is significantly
larger than the proportion among the controls. In Bayesian testing the hy-
potheses H
0
1
: p
1
> p
2
, H
00
1
: p
1
/p
2
> 1, and H
000
1
:
p
1
1−p
1
.
p
2
1−p
2
> 1 have posterior
probabilities of 0.9978 each. Therefore, in this retrospective study, smoking
status is indicated as a significant risk factor for lung cancer.

10.7 Two Poisson Rates* 387
10.7 Two Poisson Rates*
There are several methods for devising confidence intervals on differences or
the ratios of two Poisson rates. We will focus on the method for the ratio that
modifies well-known binomial confidence intervals.
Let X
1
∼ P oi(λ
1
t
1
) and X
2
∼ P oi(λ
2
t
2
) be two Poisson counts with rates
λ
1
and λ
2
observed during time intervals of length t
1
and t
2
.
We are interested the confidence interval for the ratio
λ =λ
1
/λ
2
.
Since X
1
, given the sum X
1
+ X
2
= n, is binomial B in(n, p) with p =
λ
1
t
1
λ
1
t
1
+λ
2
t
2
(Exercise 5.5), the strategy is to find the confidence interval for p
and, from its confidence bounds LB
p
and UB
p
, work out the bounds for the
ratio
λ.
LB
λ
=
LB
p
1 −LB
p
t
2
t
1
UB
λ
=
UB
p
1 −UB
p
t
2
t
1
.
For finding the LB
p
and UB
p
several methods are covered in Chap. 7. Note
that there
ˆ
p
= X
1
/n and n = X
1
+X
2
.
The design question can be addressed as well, but the “sample size” for-
mulation needs to be expressed in terms of sampling durations t
1
and t
2
.
The sampling time frames t
1
and t
2
, if assumed equal, can be determined on
the basis of elicited precision for the confidence interval and preliminary esti-
mates of the rates. Let
λ
1
and λ
2
be preexperimental assessments of the rates
and let the precision be elicited in the form of (a) the length of the interval
UB
λ
−LB
λ
=w or (b) the ratio of the bounds UB
λ
/LB
λ
=w.
Then, for achieving (1
−α)100% confidence with an interval of length w,
the sampling time frame required is
(a)
t (
= t
1
= t
2
) =
z
2
1
−α/2
³
1/λ
1
+1/λ
2
´
arcsin
³
λ
2
λ
1
×
w
2
´
and
(b)
t (
= t
1
= t
2
) =
4z
2
1
−α/2
³
1/λ
1
+1/λ
2
´
log
2
(w)
.
Example 10.14. Wire Failures. Price and Bonett (2000) provide an exam-
ple with data from Gardner and Ringlee (1968), who found that bare wire
had X
1
= 69 failures in a sample of t
1
= 1079.6 thousand foot-years, and a

388 10 Two Samples
polyethylene-covered tree wire had X
2
= 12 failures in a sample of t
2
= 467.9
thousand foot-years. We are interested in a 95% confidence interval for the
ratio of population failure rates.
The associated MATLAB file
ratiopoissons.m calculates the 95% confi-
dence interval for the ratio
λ = λ
1
/λ
2
using Wilson’s proposal (“add two suc-
cesses and two failures”). There,
ˆ
p
= (X
1
+2)/(n +4), and the interval for p
is [0.7564, 0.9141]. After transforming the bounds to the
λ domain, the final
interval is [1.3461,4.6147].
%CI for Ratio of Two Poissons
X1=69; t1 = 1079.6;
X2=12; t2=467.9;
n=X1 + X2;
phat = X1/n; %0.8519
phat1 = (X1 +2)/(n + 4); %0.8353
qhat1 = 1 - phat1; %0.1647
% Agresti-Coull CI for prop was selected.
LBp=phat1-norminv(0.975)
*
sqrt(phat1
*
qhat1/(n+4)) %0.7564
UBp=phat1+norminv(0.975)
*
sqrt(phat1
*
qhat1/(n+4)) %0.9141
LBlam = LBp/(1 - LBp)
*
t2/t1; %back to lambda
UBlam = UBp/(1 - UBp)
*
t2/t1;
[LBlam, UBlam] %[1.3461 4.6147]
%Frame size in Poisson Sampling
lambar1 = 69/1079.6; %0.0639
lambar2 = 12/467.9; %0.0256
w = 2;
td =4
*
norminv(0.995)^2
*
(1/lambar1+1/lambar2)/...
(asin(lambar2/lambar1
*
w/2)); %3511.8
tr = 4
*
norminv(0.995)^2
*
...
( 1/lambar1 + 1/lambar2 )/(log(w))^2; %3018.1
Cox (1953) gives an approximate test and confidence interval for the ratio
that uses an F distribution. He shows that the statistic
F
=
t
1
λ
1
t
2
λ
2
X
2
+1/2
X
1
+1/2
has an approximate F distribution with 2X
1
+1 and 2X
2
+1 degrees of freedom.
From this, an approximate (1
−α)100% confidence interval for λ
1
/λ
2
is
·
t
2
t
1
X
1
+1/2
X
2
+1/2
F
2X
1
+1,2X
2
+1,α/2
,
t
2
t
1
X
1
+1/2
X
2
+1/2
F
2X
1
+1,2X
2
+1,1−α/2
¸
.
Suppose we want to replicate this study using a new shipment of each type
of wire. We want to estimate the failure rate ratio with 99% confidence and
UB
λ
/LB
λ
=2. Using
λ
1
=69/1079.6 =0.0691 and
λ
2
=12/467.9 =0.0833 as our
planning estimates of λ
1
and λ
2
, we would sample t =
4(2.5758)
2
(1/0.0691+1/0.0833)
log
2
(2)
=
3018 foot-years from each shipment. If we want to complete the study in k
years, then we would sample 3018/k linear feet of wire from each shipment.
