Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

10.8 Equivalence Tests* 389

In the context of Example 10.14, the 95% conﬁdence interval for the ratio λ

/λ

is [1.3932,4.7497].

%Cox

LBlamc= t2/t1

(X1+1/2)/(X2+1/2)

finv(0.025, 2

X1+1, 2

X2+1);

UBlamc= t2/t1

(X1+1/2)/(X2+1/2)

finv(0.975, 2

X1+1, 2

X2+1);

[LBlamc, UBlamc] %1.3932 4.7497

Note that this interval does not contain 1, which is equivalent to a rejection

of H

: λ

=λ

in a test against the two-sided alternative, at the level α =0.05.

The test of H

: λ

=λ

can be conducted using the statistic

+1/2

which under H

has an F distribution with d f

= 2X

+1 and d f

= 2X

degrees of freedom.

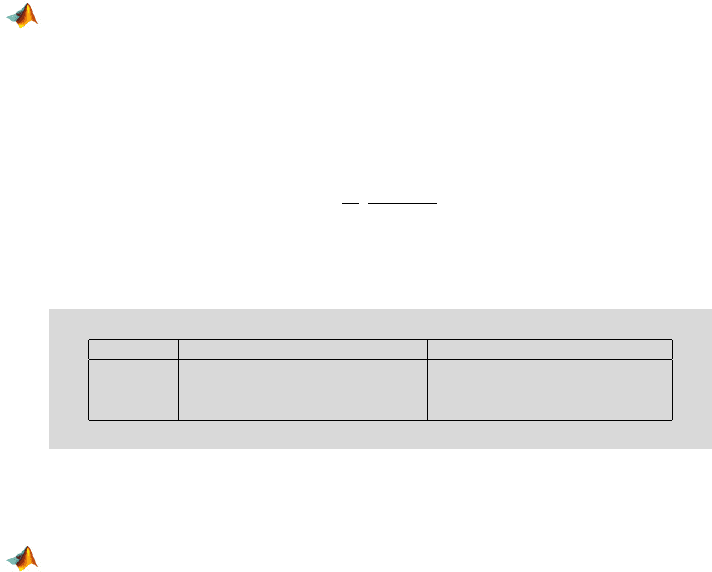
Alternative α-level rejection region p-value

: λ

<λ

d f

,d f

,1−α

,∞) 1-fcdf(F,df1,df2)

: λ

6=λ

[0, F

d f

,d f

,α/2

] ∪[F

d f

,d f

,1−α/2

,∞) 2

fcdf(min(F,1/F),df1,df2)

: λ

>λ

[0, F

d f

,d f

,α

] fcdf(F,df1,df2)

In Example 10.14, the failure rate λ

for the bare wire is found to be sig-

niﬁcantly larger (p-value of 0.00066) than that of polyethylene-covered wire,

%test against H

1: lambda1 > lambda2

pval =fcd(t1/t2

(X2+1/2)/(X1+1/2), 2

X1 + 1, 2

X2 + 1)

%6.6417e-004

10.8 Equivalence Tests*

In standard testing of two means, the goal is to show that one population mean

is signiﬁcantly smaller, larger, or different than the other. The null hypothesis

is that there is no difference between the means. By not rejecting the null,

the equality of means is not established – the test simply did not ﬁnd enough

statistical evidence for the alternative hypothesis. Absence of evidence is not

evidence of absence.

In many situations (drug and medical procedure testing, device perfor-

mance, etc.), one wishes to test the equivalence hypothesis, which states that

the population means or population proportions differ for no more than a small

tolerance value preset by a regulatory agency. If, for example, manufacturers

of a generic drug are able to demonstrate bioequivalence to the brand-name

390 10 Two Samples

product, they do not need to conduct costly clinical trials in order to demon-

strate the safety and efﬁcacy of their generic product. More importantly, es-

tablished bioequivalence protects the public from unsafe or ineffective drugs.

In this kind of inference it is desired that “no difference” constitutes the

research hypothesis H

and that signiﬁcance level α relates to the probability

of falsely rejecting the hypothesis that there is a difference when in fact the

means are equivalent. In other words, we want to control the type I error and

design the power properly in this context.

In drug equivalence testing typical measurements are the area under the

concentration curve (AUC) or maximum concentration (C

max

). The two drugs

are bioequivalent if the population means of the AUC and C

max

are sufﬁciently

close.

Let

denote the population mean AUC for the generic (test) drug and let

denote the population mean for the brand-name (reference) drug.

We are interested in testing

: η

/η

<δ

or η

/η

>δ

versus H

: δ

≤η

/η

≤δ

where

and δ

are the lower and upper tolerance limits, respectively. The

FDA recommends

=4/5 and δ

=5/4 (FDA, 2001).

This hypothesis can be tested in the domain of original measurements

(Berger and Hsu, 1996) or after taking the logarithm. This second approach

is more common in practice since (i) AUC and Cmax measurements are con-

sistent with the lognormal distribution (the pharmacokinetic rationale based

on multiplicative compartmental models) and (ii) normal theory can be applied

to logarithms of observations. The FDA also recommends a log-transformation

of data by providing three rationales: clinical, pharmacokinetic, and statistical

(FDA, 2001, Appendix D).

Since for lognormal distributions the mean

η is connected with the param-

eters of the associated normal distribution,

µ and σ

(p. 218), by assuming

equal variances we get

=exp{µ

+σ

/2} and η

=exp{µ

+σ

/2}. The equiv-

alence hypotheses for the log-transformed data now take the form

: µ

−µ

≤θ

or µ

−µ

≥θ

, versus H

: θ

<µ

−µ

<θ

where

= log(δ

) and θ

= log(δ

) are known constants. Note that if δ

1/δ

, then the bounds θ

and θ

are symmetric about zero, θ

=−θ

Equivalence testing is an active research area and many classical and

Bayesian solutions exist, as dictated by experimental designs in practice. The

monograph by Wellek (2010) provides comprehensive coverage. We focus only

on the case of testing the equivalence of two population means when unknown

population variances are the same.

TOST. Schuirmann (1981) proposed two one-sided tests (TOSTs) for testing

bioequivalence. Two t-statistics are calculated:

10.8 Equivalence Tests* 391

−X

−θ

1/n

+1/n

and t

−X

−θ

1/n

+1/n

where

and X

are test and reference means, n

and n

are test and ref-

erence sample sizes, and s

is the pooled sample standard deviation, as on

p. 357. Note that here, the test statistic involves the acceptable bounds

and θ

in the numerator, unlike the standard two-sample t-test, where the

numerator would be

−X

The TOST is now carried out as follows.

(i) Using the statistic t

, test H

: µ

−µ

=θ

versus H

: µ

−µ

>θ

(ii) Using the statistic t

, test H

: µ

−µ

=θ

versus H

: µ

−µ

<θ

(iii) Reject H

at level α, that is, declare the drugs equivalent if both hypotheses H

and H

are rejected at level α, that is, if

> t

−2,1−α

and t

< t

−2,α

Equivalently, if p

and p

are the p-values associated with statistics t

and t

, H

is rejected when max{p

, p

} <α.

Westlake’s Conﬁdence Interval. An equivalent methodology to test for

equivalence is Westlake’s conﬁdence interval (Westlake, 1976). Bioequivalence

is established at signiﬁcance level

α if a t-interval of conﬁdence (1 −2α)100%

is contained in the interval (

,θ

−X

−t

−2,1−α

1/n

+1/n

−X

−2,1−α

1/n

+1/n

∈

(θ

,θ

Here, the usual t

−2,1−α/2

is replaced by t

−2,1−α

, and Westlake’s

interval coincides with the standard (1

−2α)100% conﬁdence interval for a

difference of normal means.

Example 10.15. Equivalence of Generic and Brand-Name Drugs. A

manufacturer wishes to demonstrate that their generic drug for a particular

metabolic disorder is equivalent to a brand-name drug. One indication of the

disorder is an abnormally low concentration of levocarnitine, an amino acid

derivative, in the plasma. Treatment with the brand-name drug substantially

increases this concentration.

392 10 Two Samples

A small clinical trial is conducted with 43 patients, 18 in the brand-name

drug arm and 25 in the generic drug arm. The following increases in the log-

concentration of levocarnitine are reported.

Increase for 7 8 4 6 10 10 5 7 9 8

brand-name drug

6 7 8 4 6 10 8 9

Increase for 6 7 5 9 5 5 3 7 5 10

generic drug

2 5 8 4 4 8 6 11 7 5

5 5 7 4 6

The FDA declares that bioequivalence among the two drugs can be estab-

lished if the difference in response to the two drugs is within two units of the

log-concentration. Assuming that the log-concentration measurements follow

normal distributions with equal population variance, can these two drugs be

declared bioequivalent within a tolerance of

±2 units?

brandname = [7 8 4 6 10 10 5 7 9 ...

8 6 7 8 4 6 10 8 9 ];

generic = [6 7 5 9 5 5 3 7 5 ...

10 8 5 8 4 4 8 6 11 ...

7 5 5 5 7 4 6 ];

xbar1 = mean(brandname) %7.3333

xbar2 = mean(generic) %6.2000

s1 = std(brandname) %1.9097

s2 = std(generic) %1.9791

n1 = length(brandname) %18

n2 = length(generic) %25

sp = sqrt( ((n1-1)

s1^2 + (n2-1)

s2^2)/(n1 + n2 - 2)) % 1.9506

tL = (xbar1 - xbar2 -(-2))/(sp

sqrt( 1/n1 + 1/n2 )) % 5.1965

tU = (xbar1 - xbar2 - 2 )/(sp

sqrt( 1/n1 + 1/n2 )) %-1.4373

pL = 1-tcdf(tL, n1+ n2 - 2) %2.9745e-006

pU = tcdf(tU, n1 + n2 - 2) %0.0791

max(pL, pU) %0.0791 > 0.05, no equivalence

alpha = 0.05;

[xbar1-xbar2 - tinv(1-alpha, n1+n2-2)

sqrt(1/n1+1/n2),...

xbar1-xbar2 + tinv(1-alpha, n1+n2-2)

sqrt(1/n1+1/n2)]

% 0.1186 2.1481

% (0.1186, 2.1481) is not contained in (-2,2), no equivalence

Note that the equivalence of the two drugs was not established. The TOST

did not simultaneously reject null hypotheses H

and H

, or, equivalently,

Westlake’s interval failed to be fully included in the preset tolerance interval

(

−2,2).

Bayesian solution is conceptually straightforward. One ﬁnds the posterior

distribution for the difference of the means, and evaluates the probability of

10.9 Exercises 393

this difference falling in the interval (−2,2). The posterior probability of (−2,2)

should be close to 1 (say, 0.95) in order to declare equivalence.

model{

for(i in 1:n) {

increase[i] ~ dnorm(mu[type[i]], prec)

}

mu[1] ~ dnorm( 10, 0.00001)

mu[2] ~ dnorm( 10, 0.00001)

mudiff <- mu[1]-mu[2]

prec ~ dgamma(0.001, 0.001)

probint <- step( mudiff + 2)

step(2 - mudiff)

}

DATA

list( n=43, increase = c(7, 8, 4, 6, 10, 10, 5, 7, 9,

8, 6, 7, 8, 4, 6, 10, 8, 9, 6, 7, 5, 9, 5, 5, 3, 7, 5,

10, 8, 5, 8, 4, 4, 8, 6, 11, 7, 5, 5, 5, 7, 4, 6 ),

type = c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,

2, 2, 2, 2, 2, 2, 2))

INITS

list( mu = c(10, 10), prec = 1)

mean sd MC error val5.0pc median val95.0pc start sample

mudiff 1.133 0.6179 6.238E-4 0.117 1.133 2.147 10001 1000000

probint 0.9213 0.2693 2.766E-4 0.0 1.0 1.0 10001 1000000

The Bayesian analysis closely matches the ﬁndings by TOST and West-

lake’s interval. Note that the posterior probability of the tolerance interval

(

−2,2) is 0.9213, short of 0.95. Also, the 90% credible set (0.117,2.147) is close

to Westlake’s interval (0.1186,2.1481). This closeness is a consequence of non-

informative priors on the means and precision.

10.9 Exercises

10.1. Testing Piaget. Two groups of elementary school students are taught

mathematics by two different methods: traditional (group 1) and small

group interactive teaching by discovery based on Piagetian theory (group 2).

The results of a learning test are analyzed to test the difference in mean

scores using the two methods. Group 1 had 16 students while group 2 had

14 students and the scores are given below.

Groups Scores

Traditional 80, 69, 85, 87, 74, 85, 95, 84, 87, 86, 82, 91, 79, 100, 83, 85

Piagetian 100, 89, 87, 76, 93, 68, 99, 100, 78, 99, 100, 74, 76, 97

394 10 Two Samples

Test the hypothesis that the methods have no inﬂuence on test scores

against the alternative that the students in group 2 have signiﬁcantly

higher scores. Take

α =.05.

10.2. Smoking and COPD. It is well established that long-term cigarette

smoking is associated with the activation of a cascade of inﬂammatory

responses in the lungs that lead to tissue injury and dysfunction. This is

manifested clinically as chronic obstructive pulmonary disease (COPD). It

is believed that smoking causes approx. 80 to 90% of COPD cases.

Nine life-long nonsmoking healthy volunteers (5 men and 4 women; mean

age 22.0

±1.9 years [±SD]) and 11 healthy volunteers (5 men and 6 women;

mean age 23.4

±0.9 years) with a 2.0±1.2 pack-year cigarette smoking his-

tory were recruited from students attending the University of Illinois at

Chicago. No participants had a history of chronic respiratory tract disor-

ders, including asthma and COPD, and denied symptoms of acute respira-

tory illness within 4 weeks preceding the study.

The study by Garey et al. (2004) have found various summaries involv-

ing proteins, nitrite, and other inﬂammatory cascade signatures in exhaled

breath condensate (EBC). Average nitrite concentration in EBC of non-

smokers was found to be

= 16156 (nmol/L) and the sample standard

deviation was s

=7029 (nmol/L). For smokers the mean nitrite concentra-

tion was

= 24672 (nmol/L) with sample standard deviation s

= 7534

(nmol/L).

Assuming that the population variances are the same, test the hypothesis

that the nitrite concentration in EBC for smokers and nonsmokers are the

same versus the one-sided alternative. Use

α =5%.

10.3. Noradrenergic Activity. Although loss of noradrenergic neurons in the

locus ceruleus has been consistently demonstrated postmortem in Alzheim-

er’s disease, several studies suggest that indices of central noradrenergic

activity increase with the severity of Alzheimer’s disease in living patients.

The research by Elrod et al. (1997) estimated the effect of Alzheimer’s dis-

ease severity on central noradrenergic activity by comparing the CSF nore-

pinephrine concentrations of subjects with Alzheimer’s disease in early

and advanced stages. Lumbar punctures were performed in 29 subjects

with Alzheimer’s disease of mild or moderate severity and 17 subjects with

advanced Alzheimer’s disease. Advanced Alzheimer’s disease was deﬁned

prospectively by a mini-mental state score of less than 12. Norepinephrine

was measured by radioenzymatic assay, and it is assumed that the mea-

surements followed a normal distribution.

The CSF norepinephrine concentration for Alzheimer’s-free subjects has a

mean of 170 pg/ml. The patients with advanced Alzheimer’s disease had a

mean CSF norepinephrine concentration of 279 pg/ml, with a sample stan-

dard deviation of 122, while in those with mild to moderate severity the

mean was 198 pg/ml with a standard deviation of 89. In both cases normal-

ity is assumed.

10.9 Exercises 395

(a) Let µ

and µ

be the population means for CSF norepinephrine concen-

tration for patients with advanced and mild-to-moderate severity, respec-

tively. Test the hypotheses H

: µ

= 170 and H

: µ

= 170 based on the

available information.

(b) Test the hypothesis that the population variances are the same, H

=σ

, versus the two-sided alternative.

: µ

= µ

. Choose the type of t-test based on the

decision in (b).

In all cases use

α =0.05.

10.4. Testing Variances. Consider the following annotated MATLAB ﬁle.

%The two samples x and y are:

x = [0.34 0.52 -0.67 -0.98 -2.46 0.05 1.12 ...

1.80 -0.51 0.88 0.29 0.29 0.66 0.06 -0.29];

y = [0.70 -0.61 -1.09 1.68 -0.62 -0.57 0.41];

%Test the equality of population variances

%against the two sided alternative.

%The built-in MATLAB function

[h p]=vartest2(x, y)

gives: %h=0 (choose H0) and p-value p=0.9727.

(a) Find the p-value using MATLAB code in the table on p. 359. Does it

coincide with the

vartest2 result?

(b) Show that F

= s

> 1. In such a case the standard recommendation

is to calculate the two-sided p-value as

p = 2

(1 - fcdf(F,n1-1, n2-1)),

where

n1=length(x) and n2=length(y). Show that for the samples from this

exercise, this “p-value” exceeds 1. Can you explain what the problem is?

10.5. Mating Calls. In a study of mating calls in the gray treefrogs Hyla

hrysoscelis and Hyla versicolor, Gerhart (1994) reports that in a location

in Lousiana the following data on the length of male advertisement calls

have been collected:

Sample Average SD of Duration

size duration duration range

Hyla chrysoscelis 43 0.65 0.18 0.36–1.27

Hyla versicolor 12 0.54 0.14 0.36–0.75

The two species cannot be distinguished by external morphology, but H.

chrysoscelis are diploids while H. versicolor are tetraploids. The triploid

crosses exhibit high mortality in larval stages, and if they attain sexual

maturity, they are sterile. Females responding to the mating calls try to

avoid mismatches.

Based on the data summaries provided, test whether the length of call is a

discriminatory characteristic? Use

α =0.05.

396 10 Two Samples

10.6. Fatigue. According to the article “Practice and fatigue effects on the pro-

gramming of a coincident timing response,” published in the Journal of Hu-

man Movement Studies in 1976, practice under fatigued conditions distorts

mechanisms that govern performance. An experiment was conducted using

15 college males who were trained to make a continuous horizontal right-

to-left arm movement from a microswitch to a barrier, knocking over the

barrier coincident with the arrival of a clock’s second hand to the 6 o’clock

position. The absolute value of the difference between the time, in millisec-

onds, that it took to knock over the barrier and the time for the second hand

to reach the 6 o’clock position (500 ms) was recorded. Each participant per-

formed the task ﬁve times under prefatigue and postfatigue conditions, and

the sums of the absolute differences for the ﬁve performances were recorded

as follows:

Absolute time differences

(ms)

Subject Prefatigue Postfatigue

1 158 91

2 92 59

3 65 215

4 98 226

5 33 223

6 89 91

7 148 92

8 58 177

9 142 134

10 117 116

11 74 153

12 66 219

13 109 143

14 57 164

15 85 100

An increase in the mean absolute time differences when the task is per-

formed under postfatigue conditions would support the claim that practice

under fatigued conditions distorts mechanisms that govern performance.

Assuming the populations to be normally distributed, test this claim at

level

α =0.01.

10.7. Mosaic Virus. A single leaf is taken from each of 11 different tobacco

plants. Each leaf is then divided in half and given one of two preparations

of mosaic virus. Researchers wanted to examine if there was a difference in

the mean number of lesions from the two preparations.

Here are the raw data:

10.9 Exercises 397

Plant Prep 1 Prep 2

1 18 14

2 20 15

3 6 9

4 13 11

(a) Is this experiment in accordance with a paired t-test setup?

(b) Test the hypothesis that the difference between the two population

means,

−µ

, is signiﬁcantly positive. Use α =0.05.

10.8. Dopamine

β-hydroxylase Activity. Postmortem brain specimens from

nine chronic schizophrenic patients and nine controls were assayed for ac-

tivity of dopamine

β-hydroxylase (DBH), the enzyme responsible for the

conversion of dopamine to norepinephrine (Wyatt et al., 1975).

The means and standard deviations of DBH activity in the hippocampus

part of the brain are provided in the table. Assume that the data come from

two normally distributed and independent populations.

Schizophrenic Control

subjects subjects

Sample size n

=9 n

Sample mean

=35.5 X

=39.8

Sample standard deviation s

=6.93 s

=8.16

(a) Test to determine if the mean activity is signiﬁcantly lower for the

schizophrenic subjects than for the control subjects. Use

α =0.05.

(b) Construct a 99% conﬁdence interval for the mean difference in enzyme

activity between the two groups.

Solve the above in two ways: (i) by assuming that

= σ

and (ii) without

such an assumption.

Wyatt et al. (1975) report that one of the control subjects with low DBH

activity had unusually long death-to-morgue time (27 hours) and suggested

excluding the subject from the study. The data for controls after exclusion

were n

= 8, X

= 41.2, and s

= 7.52. Repeat the test in (a) and (b) with

these control data.

10.9. 5-HIAA Levels. A rare and slow-growing form of cancer, carcinoid tu-

mors, may develop anywhere in the body where neuroendocrine (hormone-

producing) cells exist. Serotonin is one of the key body chemicals released

by carcinoid tumors that are associated with carcinoid syndrome. The 5-

hydroxyindoleacetic acid (5-HIAA) test is a 24-hour urine test that is spe-

ciﬁc to carcinoid tumors. Elevated levels of 5-HIAA, a byproduct of sero-

tonin decomposition, can be detected from a urine sample.

Ross and Roberts (1985) provide results of a case/control study of a mor-

phologically speciﬁc type of carcinoid disorder that involves the mural and

valvular endocardium on the right side of the heart, known as carcinoid

398 10 Two Samples

heart disease. Out of a total of 36 subjects they investigate, urinary excre-

tion of 5-hydroxyindoleacetic acid (5-HIAA) was measured on 28 subjects,

16 cases with carcinoid hearth disease and 12 controls. The data (level of

5-HIAA in milligrams per 24 hours), also discussed in Dawson–Saunders

and Trapp (1994), are provided in the table below.

Patients 263 288 432 890

450 1270 220 350

283 274 580 285

524 135 500 120

Controls 60 119 153 588

124 196 14 23

43 854 400 73

Assuming that the data come from respective normal distributions, com-

pare the means of the two populations in both a classical and a Bayesian

fashion. For the Bayes model use noninformative priors.

10.10. Stress, Diet, and Acids. In the study “Interrelationships Between Stress,

Dietary Intake, and Plasma Ascorbic Acid During Pregnancy,” discussed by

Walpole et al. (2007, p. 359), the plasma ascorbic acid levels of pregnant

women were compared for smokers versus nonsmokers. Thirty-two healthy

women, between 15 and 32 years old, in the last 3 months of pregnancy

were selected for the study. Eight of the women were smokers. Prior to the

lab tests, the participants were told to avoid food and vitamin supplements.

From the blood samples, the following plasma ascorbic acid values of each

subject were determined in milligrams per 100 ml:

Plasma ascorbic acid values

Nonsmokers Smokers

0.97 1.06 0.48

0.72 0.86 0.71

1.00 0.85 0.98

0.81 0.58 0.68

0.62 0.57 1.18

1.32 0.64 1.36

1.24 0.98 0.78

0.99 1.09 1.64

0.90 0.92

0.74 0.78

0.88 1.24

0.94 1.18

(a) Using WinBUGS, test the hypothesis of equality of levels of plasma

ascorbic acid for the two populations. Use noninformative priors on pop-

ulation means and variances (precisions).

(b) Compare the results in (a) with a classical two-sample t-test with no

assumption of equality of variances.