Vidakovic B. Statistics for Bioengineering Sciences: With Matlab and WinBugs Support

Подождите немного. Документ загружается.

Chapter 11

ANOVA and Elements of Experimental

Design

Design is art optimized to meet objectives.

– Shimon Shmueli

WHAT IS COVERED IN THIS CHAPTER

• ANOVA Model Formulation

• Contrasts and Multiple Comparisons

• Factorial Designs

• Randomized Block Designs and Repeated Measures Designs

• Nested Designs

• Sample Sizes in ANOVA

• Functional ANOVA

• Analysis of Means (ANOM)

• Gauge R&R ANOVA

• Testing Equality of Proportions and Poisson Means

11.1 Introduction

In Chap. 10 we discussed the test of equality of means from two populations,

: µ

= µ

. Under standard assumptions (normality and independence) the

proper test statistic had t-distribution, and several tests (equal/different vari-

B. Vidakovic, Statistics for Bioengineering Sciences: With MATLAB and WinBUGS Support, 409

Springer Texts in Statistics, DOI 10.1007/978-1-4614-0394-4_11,

410 11 ANOVA and Elements of Experimental Design

ances, paired/unpaired samples) shared the common name “two-sample t-

tests.”

Many experimental protocols involve more than two populations. For ex-

ample, an experimenter may be interested in comparing the sizes of cells

grown under several experimental conditions. At ﬁrst glance it seems that

we can apply the t-test on all possible pairs of means. This “solution” would

not be satisfactory since the probability of type I error for such a procedure

is unduly large. For example, if the equality of four means is tested by test-

ing the equality of

6 different pairs, each at the level of 5%, then the

probability of ﬁnding a signiﬁcant difference when in fact all means are equal

is about 26.5%. We already discussed in Sect. 9.7 the problems of controlling

type I error in multiple tests.

An appropriate procedure for testing hypotheses of equality of several

means is the analysis of variance (ANOVA). ANOVA is probably one of the

most frequently used statistical procedures, and the reasoning behind it is

applicable to several other, seemingly different, problems.

11.2 One-Way ANOVA

ANOVA is an acronym for Analysis of Variance. Even though we are testing for

differences among population means, the variability among the group means

and the variability of the data within the treatment group are compared. This

technique of separating the total variability in data to between and within

variabilities is due to Fisher (1918, 1921).

Suppose we are interested in testing the equality of k means

,... , µ

char-

acterizing k independent populations

,... , P

. From the ith population P

a sample

, y

,... , y

of size n

is taken. Let N =

be the total sample size. The responses y

i j

are modeled as

i j

=µ

+²

i j

, 1 ≤ j ≤n

; 1 ≤ i ≤ k, (11.1)

where

i j

represents the “error” and quantiﬁes the stochastic variability of

difference between observation y

i j

and the mean of the corresponding popu-

lation,

. Sometimes the µ

s are called treatment means, with index i repre-

senting one of the treatments.

We are interested in testing whether all population means

are equal,

and the procedure is called one-way ANOVA. The assumptions underlying one-

way ANOVA are as follows:

(i) All populations are normally distributed;

11.2 One-Way ANOVA 411

(ii) The variances in all populations are the same and constant (assumption

of homoscedasticity);

(iii) The samples are mutually independent.

That can be expressed by the requirement that all y

i j

in (11.1) must be

i.i.d. normal

N (µ

,σ

) or, equivalently, all ²

i j

s must be i.i.d. normal N (0,σ

Normal population

1 2 . . . k

Population mean µ

. . . µ

Common variance σ

. . . σ

If the sample sizes are the same, i.e., n

= n

= ··· = n

= N/k, then the

ANOVA is called balanced. It is often the case that many experiments are

designed as a balanced ANOVA. During an experiment it may happen that a

particular measurement is missing due to a variety of reasons, resulting in an

unbalanced layout. Balanced designs are preferable since they lead to simpler

computations and interpretations.

In terms of model (11.1), the null hypothesis to be tested is

: µ

=µ

=···=µ

and the alternative is

: (H

)

(or µ

6=µ

, for at least one pair i, j.

Note that the alternative H

≡(H

)

is any negation of H

. Thus, for exam-

ple,

>µ

=µ

=···= µ

or µ

=µ

6=µ

=µ

=···= µ

are valid alternatives.

Later we will discuss how to assess the alternative if H

is rejected.

One can reparameterize the population mean

as µ

= µ +α

. Simply

speaking, the treatment mean is equal to the mean common for all treatments

(called grand mean

µ) plus the effect of the population group (treatment effect)

. The hypotheses now can be restated in terms of treatment effects:

: α

=α

=···=α

=0.

The alternative is H

: Not all α

s are equal to 0.

The representation

= µ + α

is not unique. We usually assume that

= 0. This is an identiﬁability assumption needed to ensure the unique-

ness of the decomposition

= µ +α

. Indeed, by adding and subtracting any

number c,

becomes µ +α

= (µ + c) +(α

− c) = µ

+α

, and uniqueness is

assured by

= 0. This kind of constraint is sometimes called sum-to-zero

(STZ) constraint. There are other ways to ensure uniqueness; a sufﬁcient as-

sumption is, for example,

=0. In this case µ = µ

becomes the reference or

baseline mean. Before providing the procedure for testing H

, which is sum-

marized in the ANOVA table below, we review the notation.

412 11 ANOVA and Elements of Experimental Design

i j

jth observation from treatment i

Sample mean from the treatment i

y Average of all observations

Population treatment mean

µ Population grand mean

ith treatment effect

Size of ith sample

k Number of treatments

N Total sample size

11.2.1 ANOVA Table and Rationale for F-Test

The ANOVA table displays the data summaries needed for inference about the

ANOVA hypothesis. It also provides an estimator of the variance in measure-

ments and assesses the goodness of ﬁt of an ANOVA model.

The variability in data follows the so-called fundamental ANOVA identity

in which the total sum of squares (SST) is represented as a sum of the treat-

ment sum of squares (SSTr) and the sum of squares due to error (SSE):

SST

= SST r +SSE = SS

Between

+SS

Within

i=1

j=1

i j

− y)

i=1

− y)

i=1

j=1

i j

− y

)

The standard output from most statistical software includes degrees of

freedom (DF), mean sum of squares, F ratio, and the corresponding p-value:

Source DF Sum of squares Mean squares F p

Treatment k −1 SST r MST r = SSTr/(k −1) MSTr/MSE P(F

k−1,N−k

>F)

Error N

−k SSE MSE =SSE/(N −k)

Total N −1 SST

The null hypothesis is rejected if the F-statistic is large compared to the

−α) quantile of an F distribution with k −1 and N −k degrees of freedom. A

decision can also be made by looking at the p-value.

Rationale. The mean square error, MSE, is an unbiased estimator of

Indeed,

11.2 One-Way ANOVA 413

MSE =

N −k

i=1

j=1

i j

− y

)

N −k

i=1

−1)

−1

j=1

i j

− y

)

N −k

i=1

−1)s

, and

E(MSE) =

N −k

i=1

−1)E(s

) =

N −k

i=1

−1)σ

=σ

On the other hand, mean square error due to treatments,

MST r

SSTr

k −1

i=1

− y)

is an unbiased estimator of

only when H

is true, that is, when all µ

are

the same. This follows from the fact that

E(MST r) =σ

(α

)

k −1

where

= µ

−µ is the population effect of treatment i. Since under H

= α

= ··· = α

= 0, the E(MSE) is equal to σ

, and MSTr is an unbiased

estimator of variance. When H

is violated, not all α

are 0, or, equivalently,

> 0. Thus, the ratio MST r/MSE quantiﬁes the departure from H

, and

large values of this ratio are critical.

Example 11.1. Coagulation Times. To illustrate the one-way ANOVA we

work out an example involving coagulation times that is also considered by

Box et al. (2005). Twenty-four animals are randomly allocated to 4 different

diets, but the numbers of animals allocated to different diets are not the same.

The blood coagulation time is measured for each animal. Does diet type sig-

niﬁcantly inﬂuence the coagulation time? The data and MATLAB solution are

provided next.

times = [62, 60, 63, 59, 63, 67, 71, 64, 65, 66, 68, 66, ...

71, 67, 68, 68, 56, 62, 60, 61, 63, 64, 63, 59];

diets = {’dietA’,’dietA’,’dietA’,’dietA’,’dietB’,’dietB’,...

’dietB’,’dietB’,’dietB’,’dietB’,’dietC’,’dietC’,’dietC’,...

’dietC’,’dietC’,’dietC’,’dietD’,’dietD’,’dietD’,’dietD’,...

’dietD’,’dietD’,’dietD’,’dietD’};

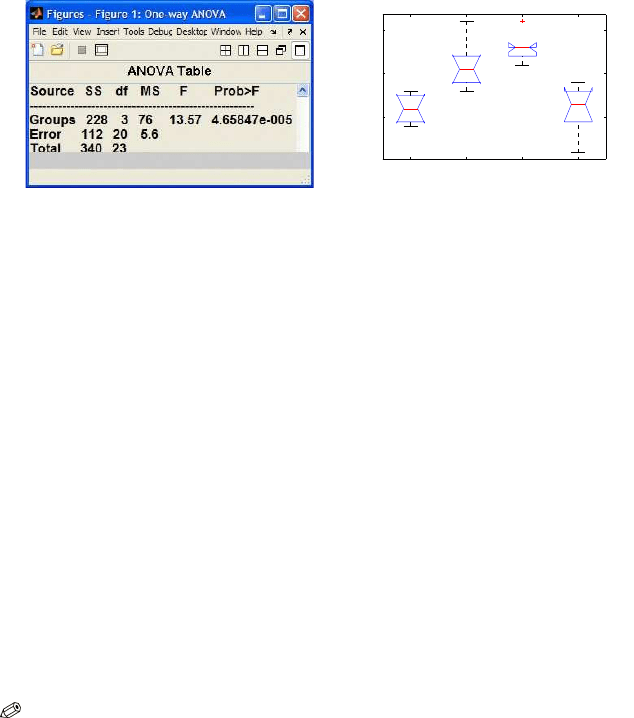
[p,table,stats] = anova1(times, diets,’on’)

% p = 4.6585e-005

% table =

%’Source’ ’SS’ ’df’ ’MS’ ’F’ ’Prob>F’

%’Groups’ [228] [ 3] [ 76] [13.5714] [4.6585e-005]

%’Error’ [112] [20] [5.6000] [] []

414 11 ANOVA and Elements of Experimental Design

%’Total’ [340] [23] [] [] []

%stats =

% gnames: 4x1 cell

% n: [4 6 6 8]

% source: ’anova1’

% means: [61 66 68 61]

% df: 20

% s: 2.3664

dietA dietB dietC dietD

(a) (b)

Fig. 11.1 (a) ANOVA table and (b) boxplots, as outputs of the

anova1 procedure on the

coagulation times data.

From the ANOVA table we conclude that the null hypothesis is not tenable,

the diets signiﬁcantly affect the coagulation time. The p-value is smaller than

0.5

·10

−4

which indicates strong support for H

The ANOVA table featured in the output and Fig. 11.1a is a standard way

of reporting the results of an ANOVA procedure. The SS column in the ANOVA

table restates the fundamental ANOVA identity SST r

+SSE =SST as 228 +

112 = 340. The degrees of freedom for treatments, k −1, and the error, n −

k, are additive and their sum is total number of degrees of freedom, n −1.

Here, 3

+20 = 23. The column with mean square errors is obtained when the

sums of squares are divided by their corresponding degrees of freedom. The

ratio F

= MST r/MSE is the test statistic distributed as F with (3, 20) degrees

of freedom. The observed F

= 13.5714 exceeds the critical value finv(0.95,

3, 20)=3.0984

, and H

is rejected. Recall that the rejection region is always

right-tailed, in this case [3.0984,

∞). The p-value is 1-fcdf(13.5714, 3, 20)=

4.6585e-005

. Figure 11.1b shows boxplots of the coagulation times by the diet

type.

Since the entries in ANOVA table are interrelated, it is possible to recover

a table from only a few entries (e.g., Exercises 11.4, 11.7, and 11.14).

11.2 One-Way ANOVA 415

11.2.2 Testing Assumption of Equal Population Variances

There are several procedures that test for the fulﬁllment of ANOVA’s condition

of homoscedasticity, that is, the condition that the variances are the same and

constant over all treatments.

A reasonably sensitive and simple procedure is Cochran’s test.

11.2.2.1 Cochran’s Test.

Cochran’s test rejects the hypothesis that k populations have the same vari-

ance if the statistic

max

+···+s

is large. Here, s

,... , s

are sample variances in k samples, and s

max

is the

largest of s

,... , s

. Cochran’s test is implemented by Cochtest.m (Trujillo-

Ortiz and Hernandez-Walls, MATLAB Central, File ID: #6431).

11.2.2.2 Levene’s Test.

Levene’s test (Levene, 1960) hinges on the statistic

(N −k)

i·

−Z

··

)

(k −1)

j=1

i j

−Z

i·

)

where Z

i j

= |y

i j

− y

i·

|. To enhance the robustness of the procedure, the sam-

ple means could be replaced by the group medians, or trimmed means. The

hypothesis H

: σ

=σ

=···=σ

is rejected at level α if L >F

k−1,N−k,α

11.2.2.3 Bartlett’s Test.

Another popular test for homoscedasticity is Bartlett’s test. The statistic

(N −k)log s

−

−1) log s

1 +

3(k−1)

×(

−1

−

N−k

)

where s

is the pooled sample variance

−1)s

+···+(n

−1)s

N−k

, has an approx-

imately

−1

distribution. Large values of B are critical, i.e., reject H

>χ

−1,α

, where α is the signiﬁcance level.

416 11 ANOVA and Elements of Experimental Design

In MATLAB, Bartlett’s test is performed by the vartestn(X) command

for samples formatted as columns of

X, or as vartestn(X, group) for vec-

tor

X, where group membership of X s is determined by the vector group.

Bartlett’s test is the default. Levene’s test is invoked by optional argument,

vartestn(...,’robust’). In the context of Example 11.1, Bartlett’s and Lev-

ene’s tests are performed in MATLAB as

% Coagulation Times: Testing Equality of Variances

[pval stats]=vartestn(times’, diets’,’on’) %Bartlet

% pval = 0.6441

% chisqstat: 1.6680

% df: 3

[pval stats]=vartestn(times’, diets’,’on’,’robust’) %Levene

% pval = 0.6237

% fstat: 0.5980

% df: [3 20]

According to these tests the hypothesis of equal treatment variances is not

rejected. Cochran’s test agrees with Bartlett’s and Levene’s, giving a p-value

of 0.6557.

Remark. As mentioned in the case of comparing the two means (p. 358), the

variances-before-means type procedures are controversial. A celebrated statis-

tician George E. P. Box criticized checking assumptions of equal variances be-

fore testing the equality means, arguing that comparisons of means are quite

robust procedures compared to a non-robust variance comparison (Box, 1953).

Aiming at Bartlett’s test in particular, Box summarized his criticism as fol-

lows: “To make the preliminary test on variances is rather putting to sea in a

rowing boat to ﬁnd out whether conditions are sufﬁciently calm for an ocean

liner to leave port!”

11.2.3 The Null Hypothesis Is Rejected. What Next?

When H

is rejected, the form for the alternative is not obvious as in the case

of two means, and thus one must further explore relationships between the

individual means. We will discuss two posttest ANOVA analyses: (i) tests for

contrasts and (ii) pairwise comparisons. They both make sense only if the null

hypothesis is rejected; if H

is not rejected, then both tests for contrasts and

pairwise comparisons are trivial.

11.2.3.1 Contrasts

A contrast is any linear combination of the population means,

11.2 One-Way ANOVA 417

C = c

+···+c

such that

=0.

For example, if

,... , µ

are means of k = 5 populations, the linear com-

binations (i) 2

−µ

, (ii) µ

−µ

, (iii) µ

+µ

−µ

−2µ

, etc. are all

contrasts since 2

−1 +0 −1 +0 =0, 0 −1 +1 +0 +0 =0, and 1 +1 +1 −1 −2 =0.

In the ANOVA model, y

i j

= µ

+²

i j

, i = 1,..., k; j = 1, ..., n

, sample treat-

ment means

j=1

i j

are the estimators of the population treatment

means

. Let N = n

+···+ n

be the total sample size and s

= MSE the

estimator of variance.

The test for a contrast

i=1

=0 versus H

i=1

<,6=,>0 (11.2)

is based on the test statistic that involves sample contrast c

t =

that has a t-distribution with N − k degrees of freedom. Here,

C =

is an estimator of contrast C and s

is the sample vari-

ance of

The (1

−α)100% conﬁdence interval for the contrast is





i=1

−t

N−k,1−α/2

·s ·

i=1

N−k,1−α/2

·s ·

i=1





Sometimes, contrast tests are called single-degree F-tests because of the

link between t- and F-distributions. Recall that if random variable X has a

t-distribution with n degrees of freedom, then X

has an F-distribution with

1 and n degrees of freedom. Thus, the test of contrast in (11.2) against the

two-sided alternative can equivalently be based on the statistic

418 11 ANOVA and Elements of Experimental Design

F =

which has an F-distribution with 1 and N

−k degrees of freedom. This F-test

is good only for two-sided alternatives since the direction of deviation from H

is lost by squaring the t-statistic.

Example 11.2. As an illustration, let us test the hypothesis H

: µ

+µ

=µ

in the context of Example 11.1. The above hypothesis is a contrast since

it can be written as

= 0 with c =(1,1,−1,−1). The following MATLAB

code tests the contrast against the one-sided alternative and also ﬁnds the

95% conﬁdence interval for

m = stats.means %[p,table,stats] = anova1(times, diets)

%from Example Coagulation Times

c = [ 1 1 -1 -1 ];

L = c(1)

m(1) + c(2)

m(2)+c(3)

m(3) + c(4)

m(4) %L=-2

LL= m

c’ %LL=-2

stdL = stats.s

sqrt(c(1)^2/4+c(2)^2/6+c(3)^2/6+c(4)^2/8)

%stdL = 1.9916

t = LL/stdL %t =-1.0042

%test H

o: mu

c’ = 0 H

1: mu

c’ < 0

% p-value

tcdf(t, 23) %0.1629

%or 95% confidence interval for population contrast

[LL - tinv(0.975, 23)

stdL, LL + tinv(0.975, 23)

stdL]

% -6.1200 2.1200

The hypothesis H

: µ

+µ

= µ

+µ

is not rejected, and the p-value is

0.1629. Also, the conﬁdence interval for

+µ

−µ

is [−6.12,2.12].

Orthogonal Contrasts*. Two or more contrasts are called orthogonal if

their sample counterpart contrasts are uncorrelated. Operationally, two con-

trasts c

+···+ c

and d

+···+d

are orthogonal if in

addition to

=0, the condition c

+···+c

holds. For unbalanced designs the condition is

=0.

If there are k treatments, only k

−1 mutually orthogonal contrasts can be

constructed. Any additional contrast can be expressed as a linear combination

of the original k

−1 contrasts. For example, if

Treatments

Contrast 1 2 3 4

1 –1 –1 1

1 0 0 –1

0 1 –1 0