Wai-Fah Chen.The Civil Engineering Handbook

Подождите немного. Документ загружается.

Physical Water and Wastewater Treatment Processes 9-49

Except for the Stokes, Newton, Allen, and Shepherd laws, the calculation of the terminal settling velocity

is iterative, because the drag coefﬁcient is a polynomial function of the velocity. Graphical solutions are

presented by Camp (1936a), Fair, Geyer, and Morris (1954), and Anderson (1941).

Nonspherical particles can be characterized by the ratios of their diameters measured along their

principal axes of rotation. Spherical and nonspherical particles are said to be “equivalent,” if they have

the same volume and weight. If Re is less than 100 and the ratios are 1:1:1 (as in a cube), the nonspherical

particles settle at 90 to 100% of the velocity of the equivalent sphere (Task Committee, 1975). For ratios

of 4:1:1, 4:2:1, or 4:4:1, the velocity of the nonspherical particle is about two-thirds the velocity of the

equivalent sphere. If the ratios are increased to 8:1:1, 8:2:1, or 8:4:1, the settling velocity of the nonspherical

particles falls to a little more than half that of the equivalent sphere. The shape problem is lessened by

the fact that ﬂoc particles are formed by the drag force into roughly spherical or teardrop shapes.

In practice, Eqs. (9.138) through (9.150) are almost never used to calculate settling velocities. The

reason for this is the onerous experimental and computational work load their use requires. Floc particles

come in a wide range of sizes, and the determination of the size distribution would require an extensive

experimental program. Moreover, the speciﬁc gravity of each size class would be needed. In the face of

this projected effort, it is easier to measure settling velocities directly using a method like Seddon’s, which

is described below.

The settling velocity equations are useful when experimental data obtained under one set of conditions

must be extrapolated to another. For example, terminal settling velocities depend on water temperature,

because temperature strongly affects viscosity. The ratio of water viscosities for 0 to 30°C, which is the

typical range of raw water temperatures in the temperature zone, is about 2.24. This means that a settling

tank designed for winter conditions will be between 1.50 and 2.24 times as big as a tank designed for

summer conditions, depending on the Reynolds number.

The terminal velocity also varies with particle diameter and speciﬁc gravity. Because particle size and

density are inversely correlated, increases in diameter tend to be offset by decreases in speciﬁc gravity,

and some intermediate particle size will have the fastest settling velocity. This is the reason for the

traditional advice that “pinhead” ﬂocs are best.

Settling Velocity Measurement

The distribution of particle settling velocities can be determined by the method ﬁrst described by Seddon

(1889) and further developed by Camp (1945). Tests for the measurement of settling velocities must be

continued for at least as long as the intended settling zone detention time. Furthermore, samples must

be collected at several time intervals in order to determine whether the concentration trajectories are

linear or concave downwards.

A vertical tube is ﬁlled from the bottom with a representative sample of the water leaving the ﬂoccu-

lation tank, or any other suspension of interest. The depth of water in the tube should be at least equal

to the expected depth of the settling zone, and there should be several sampling ports at different depths.

The tube and the sample in it should be kept at a constant, uniform temperature to avoid the development

of convection currents. A tube diameter at least 100 times the diameter of the largest particle is needed

to avoid measurable “wall effects” (Dryden, Murnaghan, and Bateman, 1956). The effect of smaller

tube/particle diameter ratios can be estimated using McNown’s (Task Committee, 1975) formula:

(9.151)

where d

= the particle’s diameter (m or ft)

= the tube’s diameter (m or ft)

= the particle’s free terminal settling velocity (m/s or ft/sec)

= the particle’s settling velocity in the tube (m/s or ft/sec)

=+ +

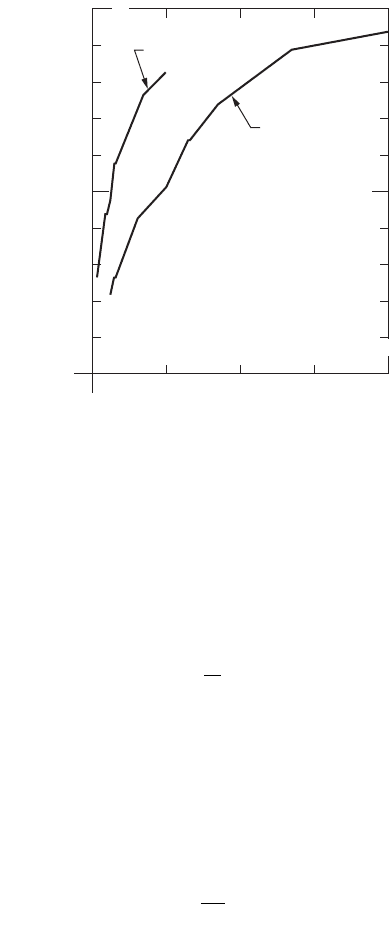
9-50 The Civil Engineering Handbook, Second Edition

The largest expected ﬂocs are on the order of a few mm in diameter, so the minimum tube diameter

will be tens of cm.

Initially, all the various particle velocity classes are distributed uniformly throughout the depth of the

tube. Therefore, at any particular sampling time after the settling begins, say t

the particles sampled at

a distance h below the water surface must be settling at a velocity less than,

(9.152)

where h

= the depth below the water’s surface of the sampling port for the i-th sample (m or ft)

= the i-th sampling time (sec)

= the limiting velocity for the particles sampled at t

(m/s or ft/sec)

The weight fraction of particles that are slower than this is simply the concentration of particles in

the sample divided by the initial particle concentration:

(9.153)

where P

= the weight fraction of the suspended solids that settle more slowly than n

(dimensionless)

= the suspended solids concentration in the sample collected at t

(kg/m

or lb/ft

)

= the initial, homogeneous suspended solids concentration in the tube (kg/m

or lb/ft

)

The results of a settling column test would look something like the data in Fig. 9.6, which are taken

from Seddon’s paper. The data represent the velocities of river muds, which are slower than alum or iron

ﬂocs.

Flocculent versus Nonﬂocculent Settling

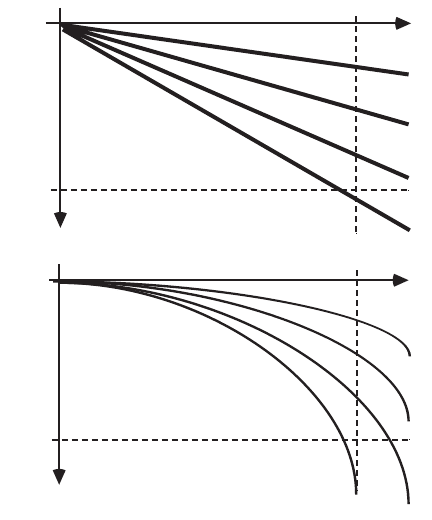
In nonﬂocculent settling, the sizes and velocities of the particles do not change. Consequently, if the

trajectory of a particular concentration is plotted on depth-time axes, a straight line is obtained. In

ﬂocculent settling, the particles grow and accelerate as the settling test progresses, and the concentration

FIGURE 9.6 Settling velocity distributions for Mississippi River sediments. [Seddon, J.A. 1889. Clearing Water by

Settlement, J. Assoc. Eng’g Soc., 8(10): 477.]

2 ft sample

8 ft sample

Fraction

slower,

velocity, n (ft/hr)

1.0

0.8

0.6

0.4

0.2

01234

Physical Water and Wastewater Treatment Processes 9-51

trajectories are concave downwards. These two possibilities are shown in Fig. 9.7. The same effect is seen

in Fig. 9.6, where the samples from 8 ft, which represent longer sampling times, yield higher settling

velocities than the 2 ft samples.

Design of Rectangular Clariﬁers

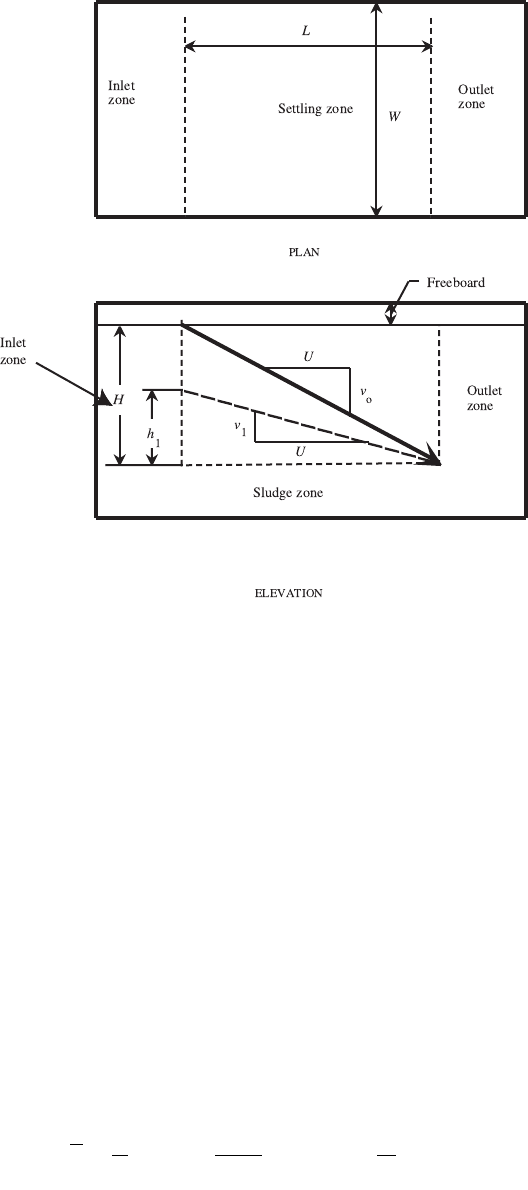
What follows is the Hazen (1904)–Camp (1936a, 1936b) theory of free settling in rectangular tanks. Refer

to Fig. 9.8. The liquid volume of the tank is divided into four zones: (1) an inlet or dispersion zone, (2) a

settling zone, (3) a sludge zone, and (4) an outlet or collection zone (Camp, 1936b).

The inlet zone is supposed to be constructed so that each velocity class of the incoming suspended

particles is uniformly distributed over the tank’s transverse vertical cross section. A homogeneous dis-

tribution is achieved in many water treatment plants as a consequence of the way ﬂocculation tanks and

rectangular settling tanks must be connected. It is not achieved in circular tanks or in rectangular tanks

in sewage treatment plants, unless special designs are adopted.

The sludge zone contains accumulated sludge and sludge removal equipment. Particles that enter the

sludge zone are assumed to remain there until removed by the sludge removal equipment. Scour of the

sludge must be prevented. Sludge thickening and compression also occur in the sludge zone, but this is

not normally considered in clariﬁer design.

The water ﬂow through the settling zone is supposed to be laminar and horizontal, and the water

velocity is supposed to be the same at each depth. Laminar ﬂow is readily achievable by bafﬂing, but the

resulting water velocities are not uniform, and often they are not horizontal. The corrections needed for

these conditions are discussed below.

The outlet zone contains the mechanisms for removing the clariﬁed water from the tank. Almost

always, water is removed from near the water surface, so the water velocity in the outlet zone has a net

upwards component. This upwards component may exceed the settling velocities of the slowest particles,

so it is assumed that any particle that enters the outlet zone escapes in the tank efﬂuent.

FIGURE 9.7 Particle depth-time trajectories for nonﬂocculent and ﬂocculent settling.

Settling time t

Settling time

Depth

Flocculent

settling

Nonflocculent

settling

9-52 The Civil Engineering Handbook, Second Edition

There are ﬁve problems that need to be considered in rectangular clariﬁer design: (1) sedimentation

of the ﬂoc particles out of the settling zone and into the sludge zone, (2) the settling velocity distribution

of the ﬂoc particles, (3) scour and resuspension of settled particles from the sludge zone, (4) turbulence

in the settling zone, and (5) short-circuiting of the ﬂow.

Sedimentation

Suppose that the settling occurs in Camp’s ideal rectangular clariﬁer, and the horizontal water velocity

is steady and uniform. In this case, column test sampling time may be equated with time-of-travel through

the settling zone, and the depth–time plot of concentration trajectories in a settling column is also a plot

of the trajectories in the settling zone. The settling zone can be represented in Fig. 9.7 by drawing a

horizontal line at the settling zone depth, H, and a vertical line at its hydraulic retention time, t.

Trajectories that cross the horizontal line before t represent those particles that are captured and enter

the sludge zone. Trajectories that cross the vertical line above H represent those particles that escape

capture and appear in the tank efﬂuent.

The ﬂow-weighted average concentration in the efﬂuent can be estimated by a simple depth average

over the outlet plane:

(9.154)

FIGURE 9.8 Settling tank deﬁnition sketch [after Camp, T.R. 1936. A Study of the Rational Design of Settling Tanks,

Sewage Works J., 8 (5): 742].

CdQ

UWH

CUW dh

Cdh

HHH

= ◊ = ◊ = ◊

ÚÚÚ

11 1

000

Physical Water and Wastewater Treatment Processes 9-53

where C = the suspended solids’ concentration at depth h (kg/m

or lb/ft

)

—

= the depth-averaged suspended solids’ concentration over the settling zone outlet’s outlet

plane (kg/m

or lb/ft

)

H = the settling zone’s depth (m or ft)

L = the settling zone’s length (m or ft)

Q = the ﬂow through the settling zone (m

/s or ft

/sec)

U = the horizontal water velocity through the settling zone (m/s or ft/sec)

W = the settling zone’s width (m or ft)

The settling zone particle removal efﬁciency is (San, 1989),

(9.155)

where C

= the suspended solids’ concentration in the inﬂuent ﬂow to the settling zone (kg/m

or lb/ft

)

E = the removal efﬁciency (dimensionless)

f = the fraction removed at each depth at the outlet plane of the settling zone (dimensionless)

The removal efﬁciency can also be calculated from the settling velocity distribution, such as in Fig. 9.6

(Sykes, 1993):

(9.156)

where P = the weight fraction of the suspended solids that settles more slowly than n (dimensionless)

= the weight fraction of the suspended solids that settles more slowly than n

(dimensionless)

n =any settling velocity between zero and n

(m/s of ft/sec)

= the tank overﬂow rate (m/s or ft/sec) (See below.)

Note that the integration is performed along the vertical axis, and the integral represents the area

between the velocity distribution curve and the vertical axis. The limiting velocities are calculated using

Eq. (9.152) by holding the sampling time t

constant at t and using concentration data from different

depths. Equation (9.156) reduces to the formulas used by Zanoni and Blomquist (1975) to calculate

removal efﬁciencies for ﬂocculating suspensions.

Nonﬂocculent Settling

Certain simpliﬁcations occur if the settling process is nonﬂocculent. However, nonﬂocculent settling is

probably limited to grit chambers (Camp, 1953). Referring to Fig. 9.8, the critical particle trajectory goes

from the top of the settling zone on the inlet end to the bottom of the settling zone on the outlet end.

The settling velocity that produces this trajectory is n

. Any particle that settles at n

or faster is removed

from the ﬂow. A particle that settles more slowly than n

, say v

, is removed only if it begins its trajectory

within h

of the settling zone’s bottom. Similar triangles show that this critical settling velocity is also

the tank overﬂow rate, and to the ratio of the settling zone depth to hydraulic retention time:

(9.157)

where n

= the critical particles’ settling velocity (m/s or ft/sec).

In nonﬂocculent free settling, the settling velocity distribution does not change with settling time, and

the efﬁciency predicted by Eq. (9.156) depends only on overﬂow rate, regardless of the combination of

depth and detention time that produces it. Increasing the overﬂow rate always reduces the efﬁciency, and

reducing the overﬂow rate always increases it.

fdh

= ◊

vdP

=- + ◊

9-54 The Civil Engineering Handbook, Second Edition

Flocculent Settling

This is not the case in ﬂocculent settling. Consider a point on one of the curvilinear contours shown in

Fig. 9.7. Equation (9.152) now represents the average velocity of the selected concentration up to the

selected instant. In the case of the contour that exits the settling zone at its bottom, the slope of the chord

is v

. The average velocity of any given contour increases as the sampling time increases. This has several

consequences:

• Fixing nn

and increasing both H and tt

increases the efﬁciency.

• Fixing nn

and reducing both H and tt

reduces the efﬁciency.

•Increasing nn

by increasing both H

and tt

may increase, decrease, or not change the efﬁciency

depending on the trajectories of the contours; if the curvature of the contours is large, efﬁciency

increases will occur for new overﬂow rates that are close to the original nn

•Reducing nn

by reducing both H and tt

may increase, decrease, or not change the efﬁciency,

depending on the trajectories of the contours; if the curvature of the contours is large, efﬁciency

reductions will occur for new overﬂow rates that are close to the original nn

Any other method of increasing or decreasing n

yields the same results as those obtained in nonﬂoc-

culent settling.

Scour

Settling zone depth is important. The meaning of Eq. (9.157) is that if a particle’s settling velocity is

equal to the overﬂow rate, it will reach the top of the sludge zone. However, once there, it still may be

scoured from the sludge zone and resuspended in the ﬂow. Repeated depositions and scourings would

gradually transport the particle through the tank and into the efﬂuent ﬂow, resulting in clariﬁer failure.

Whether or not this happens depends on the depth-to-length ratio of the settling zone.

Camp (1942) assumes that the important variable is the average shearing stress in the settling

zone/sludge zone interface. In the case of steady, uniform ﬂow, the accelerating force due to the weight

of the water is balanced by retarding forces due to the shearing stresses on the channel walls and ﬂoor

(Yalin, 1977):

(9.158)

The shearing stress depends on the water velocity and the settling zone depth. The critical shearing

stress is that which initiates mass movement in the settled particles. Dimensional analysis suggests a

correlation of the following form (Task Committee, 1975):

(9.159)

where d

= the particle’s diameter (m or ft)

= the boundary Reynolds number (dimensionless)

= n

= the shear velocity (m/s or ft/sec)

g = the speciﬁc weight of the liquid (N/m

or lbf/ft

)

= the speciﬁc weight of the particle (N/m

or lbf/ft

)

n = the kinematic viscosity of the liquid (m

/s or ft

/sec)

r= the density of the liquid (kg/m

or slug/ft

)

= the critical shearing stress that initiates particle movement (N/m

or lbf/ft

)

HS=

()

f Re

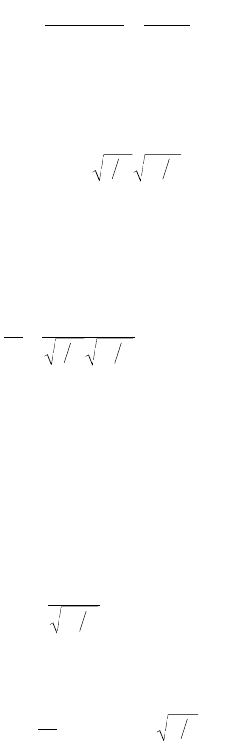
Physical Water and Wastewater Treatment Processes 9-55

Equation (9.159) applies to granular, noncohesive materials like sand. Alum and iron ﬂocs are cohesive.

The cohesion is especially well-developed on aging, and individual ﬂoc particles tend to merge together.

However, a conservative assumption is that the top layer of the deposited ﬂoc, which is fresh, coheres

weakly.

For the conditions in clariﬁers, Eq. (9.159) becomes (Mantz, 1977),

(9.160)

This leads to relationships among the settling zone’s depth and length. For example, the horizontal

velocity is related to the critical shearing stress by the following (Chow, 1959):

(9.161)

where f = the Darcy-Weisbach friction factor (dimensionless)

= the critical horizontal velocity that initiates particle movement (m/s or ft/sec).

Consequently,

(9.162)

Equation (9.162) is a lower limit on the depth-to-length ratio.

Ingersoll, McKee, and Brooks (1956) assume that the turbulent ﬂuctuations in the water velocity at

the interface cause scour. They hypothesize that the deposited ﬂocs will be resuspended if the vertical

ﬂuctuations in the water velocity at the sludge interface are larger than the particle settling velocity. Using

the data of Laufer (1950), they concluded that the vertical component of the root-mean-square velocity

ﬂuctuation of these eddies is approximately equal to the shear velocity, and they suggested that scour

and resuspension will be prevented if,

(9.163)

This leads to the following:

(9.164)

The Darcy–Weisbach friction factor for a clariﬁer is about 0.02, so the right-hand-side of Eq. (9.164)

is between 0.06 and 0.1, which means that the length must be less than 10 to 16 times the depth. Camp’s

criterion would permit a horizontal velocity that is 2 to 4 times as large as the velocity permitted by the

Ingersoll–McKee–Brooks analysis.

Short-Circuiting

A tank is said to “short-circuit” if a large portion of the inﬂuent ﬂow traverses a small portion of the

tank’s volume. In extreme cases, some of the tank’s volume is a “dead zone” that neither receives nor

discharges liquid. Two kinds of short-circuiting occur: “density currents” and “streaming.”

Density Currents

Density currents develop when the density of the inﬂuent liquid is signiﬁcantly different from the density

of the tank’s contents. The result is that the inﬂuent ﬂow either ﬂoats over the surface of the tank or

()

030

= 8 tr

≥ =

8 tr

a constant

> 1.2 to 2.0

()

1.2 to 2.0 8

9-56 The Civil Engineering Handbook, Second Edition

sinks to its bottom. The two common causes of density differences are differences in (1) temperature

and (2) suspended solids concentrations.

Te mperature differences arise because the histories of the water bodies differ. For example, the inﬂuent

ﬂow may have been drawn from the lower portions of a reservoir, while the water in the tank may have

been exposed to surface weather conditions for several hours. Small temperature differences can be

signiﬁcant.

Suspended solids have a similar effect. The speciﬁc gravity of a suspension can be calculated as follows

(Fair, Geyer, and Morris, 1954):

(9.165)

where f

= the weight fraction of water in the suspension (dimensionless)

= the speciﬁc gravity of the particles (dimensionless)

= the speciﬁc gravity of the suspension (dimensionless)

= the speciﬁc gravity of the water (dimensionless)

By convention, all speciﬁc gravities are referenced to the density of pure water at 3.98°C, where it

attains its maximum value. Equation (9.165) can be written in terms of the usual concentration units of

mass/volume as follows:

(9.166)

where X = the concentration of suspended solids (kg/m

or slug/ft

)

r = the density of water (kg/m

or slug/ft

)

Whether or not the density current has important effects depends on its location and its speed (Eliassen,

1946; Fitch, 1957). If the inﬂuent liquid is lighter than the tank contents and spreads over the tank surface,

any particle that settles out of the inﬂuent ﬂow enters the stagnant water lying beneath the ﬂow and

settles vertically all the way to the tank bottom. During their transit of the stagnant zone, the particles

are protected from scour, so once they leave the ﬂow, they are permanently removed from it. If the

inﬂuent liquid spreads across the entire width of the settling zone, then the density current may be

regarded as an ideal clariﬁer. In this case, the depth of the settling zone is irrelevant. Clearly, this kind

of short-circuiting is desirable.

If the inﬂuent liquid is heavier than the tank contents, it will settle to the bottom of the tank. As long

as the ﬂow uniformly covers the entire bottom of the tank, the density current may be treated as an ideal

clariﬁer. Now, however, the short-circuiting ﬂow may scour sludge from the tank bottom. The likelihood

of scour depends on the velocity of the density current. According to von Karman (1940), the density

current velocity is:

(9.167)

where g = the acceleration due to gravity (9.80665 m/s

or 32.174 ft/sec

)

Q = the ﬂow rate of the density current (m

/s or ft

/sec)

= the velocity of the density current (m/s or ft/sec)

W = the width of the clariﬁer (m or ft)

r = the density of the liquid in the clariﬁer (kg/m

or slug/ft

)

= the density of the density current (kg/m

or slug/ft

)

fS f S

wp w w

()

=+◊ -

()

Physical Water and Wastewater Treatment Processes 9-57

Streaming

Density currents divide the tank into horizontal layers stacked one above the other. An alternative

arrangement would be for the tank to be divided into vertical sections placed side-by-side. The sections

would be oriented to run the length of the tank from inlet to outlet. Fitch (1956) calls this ﬂow

arrangement “streaming.”

Suppose that the ﬂow consists of two parallel streams, each occupying one-half of the tank width. A

fraction f of the ﬂow traverses the left section, and a fraction 1 – f traverses the right section. Within

each section, the ﬂow is distributed uniformly over the depth. The effective overﬂow rate for the left-

hand section is v

, and a weight fraction P

settles slower than this. For the right-hand section, the overﬂow

rate is v

, and the slower fraction is P

. The ﬂow-weighted average removal efﬁciency would be:

(9.168)

This can also be written as:

(9.169)

The ﬁrst line on the right-hand side is the removal efﬁciency without streaming. The second and third

lines represent corrections to the ideal removal efﬁciency due to streaming. Fitch shows that both

corrections are always negative, and the effect of streaming is to reduce tank efﬁciency. The degree of

reduction depends on the shape of the velocity distribution curve and the design surface loading rate.

The fact that tanks have walls means that some streaming is inevitable: the drag exerted by the walls

causes a lateral velocity distribution. However, more importantly, inlet and outlet conditions must be

designed to achieve and maintain uniform lateral distribution of the ﬂow. One design criterion used to

achieve uniform lateral distribution is a length-to-width ratio. The traditional recommendation was that

the length-to-width ratio should lie between 3:1 and 5:1 (Joint Task Force, 1969). However, length-to-

width ratio restrictions are no longer recommended (Joint Committee, 1990). It is more important to

prevent the formation of longitudinal jets. This can be done by properly designing inlet details.

The speciﬁcation of a surface loading rate, a length-to-depth ratio, and a length-to-width ratio uniquely

determine the dimensions of a rectangular clariﬁer and account for the chief hydraulic problems encoun-

tered in clariﬁcation.

Traditional Rules of Thumb

Some regulatory authorities specify a minimum hydraulic retention time, a maximum horizontal velocity,

or both: e.g., for water treatment (Water Supply Committee, 1987),

(9.170)

(9.171)

Ef P

vdP f P

vdP

= ◊ -+ ◊

()

◊ -+ ◊

ÚÚ

vdP

fP P

vdP

fP P

vdP

=- + ◊

()

- ◊

()

+ ◊

t= ≥

WHL

4 hr

=£0.5 fpm

9-58 The Civil Engineering Handbook, Second Edition

Hydraulic detention times for primary clariﬁers in wastewater treatment tend to be 2 h at peak ﬂow

(Joint Task Force, 1992).

Some current recommendations for the overﬂow rate for rectangular and circular clariﬁers for water

treatment are (Joint Committee, 1990):

Lime/soda softening —

low magnesium, v

= 1700 gpd/ft

high magnesium, v

= 1400 gpd/ft

Alum or iron coagulation —

turbidity removal, v

= 1000 gpd/ft

color removal, v

= 700 gpd/ft

algae removal, v

= 500 gpd/ft

The recommendations for wastewater treatment are (Wastewater Committee, 1990):

Primary clariﬁers —

average ﬂow, v

= 1000 gpd/ft

peak hourly ﬂow, v

= 1500 to 3000 gpd/ft

Activated sludge clariﬁers, at peak hourly ﬂow, not counting recycles —

conventional, v

= 1200 gpd/ft

extended aeration, v

= 1000 gpd/ft

second stage nitriﬁcation, v

= 800 gpd/ft

Tr ickling ﬁlter humus tanks, at peak hourly ﬂow —

= 1200 gpd/ft

The traditional rule-of-thumb overﬂow rates for conventional rectangular clariﬁers in alum coagula-

tion plants are 0.25 gal/min·ft

(360 gpd/ft

) in regions with cold winters and 0.38 gal/min·ft

(550 gpd/ft

) in regions with mild winters. The Joint Task Force (1992) summarizes an extensive survey

of the criteria used by numerous engineering companies for the design of wastewater clariﬁers. The

typical practice appears to be about 800 gpd/ft

at average ﬂow for primary clariﬁers and 600 gpd/ft

for

secondary clariﬁers. The latter rate is doubled for peak ﬂow conditions.

Typical side water depths for all clariﬁers is 10 to 16 ft. Secondary wastewater clariﬁers should be

designed at the high end of the range.

Hudson (1981) reported that in manually cleaned, conventional clariﬁers, the sludge deposits often

reach to within 30 cm of the water surface near the tank inlets, and scour velocities range from 3.5 to

40 cm/sec. The sludge deposits in manually cleaned tanks are often quite old, at least beneath the surface

layer, and the particles in the deposits are highly ﬂocculated and “sticky.” Also, the deposits are well-

compacted, because there is no mechanical collection device to stir them up. Consequently, Hudson’s

data represent the upper limits of scour resistance.

The limit on horizontal velocity, Camp’s shearing stress criterion, and the Ingersoll–McKee–Brook’s

velocity ﬂuctutation criterion are different ways of representing the same phenomenon. In principle, all

three criteria should be consistent and produce the same length-to-depth ratio limit. However, different

workers have access to different data sets and draw somewhat different conclusions. Because scour is a

major problem, a conservative criterion should be adopted. This means a relatively short length-to-depth

ratio, which means a relatively deep tank.

The limits on tank overﬂow rate, horizontal velocity, length-to-depth ratio, and hydraulic retention

time overdetermine the design; only three of them are needed to specify the dimensions of the settling

zone. They may also be incompatible.

Design of Circular Tanks

In most designs, the suspension enters the tank at the center and ﬂows radially to the circumference.

Other designs reverse the ﬂow direction, and in one proprietary design, the ﬂow enters along the

circumference and follows a spiral path to the center.