Яковлев Н.В. и др. Практикум по высшей геодезии. Вычислительные работы

Подождите немного. Документ загружается.

Раскладывая (17.12) в ряд Тейлора, получим

= hf;

j 2 *

aM +

TPV

где f=f (x

, y

Подставляя Формулу (17.13) в (17.11), получим

Л (Yi

)

f +

(«

+ Р

1 / а

/ а/ d

/ \

+ 1" ** -ф +

2cc

$iof + PV -фу

(17

л4)

Разложение точного решения имеет вид •

h*(

*f a. Of JLx« ^ . ,

f \ , (17 1СЧ

Сравнивая соответствующие коэффициенты при ft/, ft

-^-»

в формулах (17.15) и (17.14), получим

7I + Y

; Y2

;

O = 4"' (17.16)

откуда

Vi =

— v

, (17.17)

где Y2—произвольная не равная нулю постоянная.

При Y2=0,5 получим

У1 = Уо+-%- (*i + = V(*o. Уо)\

= hf(x

+ h, y

+kj. (17.18)

Формулы (17.18) являются решением по методу Рунге — Кут-

та 2-го порядка. При £=1,2 п получим в общем случае более

точные формулы Рунге — Кутта п-го порядка.

Решение (17.18) имеет простой геометрический смысл. В точке

(хо, уо) вычисляется тангенс угла наклона kjh функции у =

<р

(х).

Используя его, продвигаются на шаг h вперед и вычисляют тан-

генс угла наклона k

/h. Каждый тангенс угла наклона имеет вес,

равный единице. Среднее значение тангенса из двух вычисленных

принимают за окончательный, чтобы сделать шаг от (х

, у

) к

(*ь У\)-

Пробные шаги, которые дают информацию для окончательного

решения, можно планировать различными способами. Метод вы-

279

бора пробных точек влияет на точность и эффективность решения.

Этим обстоятельством можно объяснить появление модификаций

классического метода Рунге — Кутта, которые отличаются боль-

шой эффективностью решения. Из современных модификаций

наиболее удобным в практическом отношении оказался метод

Рунге — Кутта — Ингланда, который дает возможность надежно

оценить точность решения, не определяемую в обычном методе

Рунге— Кутта.

Метод Рунге—Кутта — Ингланда в настоящее время является

наиболее оптимальным по точности и эффективности решения пря-

мой геодезической задачи на любые расстояния.

Обратная геодезическая задача принципиально может быть

решена методом Рунге — Кутта и его модификациями. Однако

практическая реализация метода в этом случае требует итераци-

онного решения, снижая, таким образом, его эффективность по

сравнению с существующим методом Гаусса.

Поэтому наилучшим численным методом для решения обрат-

ной геодезической задачи на малые и средние расстояния являет-

ся метод Гаусса, основанный на разложении подынтегральной

функции (17.5) в ряд по средним аргументам.

В основу существующих методов решения главных геодезичес-

ких задач для больших расстояний положена идея Бесселя, в со-

ответствии с которой от геодезических элементов на эллипсоиде

переходят к вспомогательной сфере, осуществляя на ней решение

полярного сферического треугольника и определяя искомые вели-

чины. После этого вычисляют и вводят в решение поправки, не-

обходимые для перехода вновь на поверхность эллипсоида.

Практическая реализация этой идеи, т. е. формул Бесселя, свя-

зана с трудностями вычислений эллиптических интегралов.

Существующие модификации формул Бесселя направлены на

аппроксимирование подынтегральной функции аналитическим вы-

ражением, удобным для практических расчетов.

В последующих параграфах изложены алгоритмы наиболее

оптимальных в настоящее время методов решения главных геоде-

зических задач.

Метод Рунге — Кутта — Ингланда [И] состоит в том, что ре-

шение дифференциального уравнения первого порядка в точке

Xj+i имеет вид

§ 88. Решение прямой геодезической задачи

методом Рунге — Кутта — Ингланда

yj+i = yj+"$ +

4к

з -f*4)>

(17.19)

где

280;

= Ах/ [xj + bx, yj + 0,25 (k

+ 6

)j;

= Дд/ (x

- + Дх, yj — k

+ 2£

Дх = х/-ы—X/ — шаг интегрирования.

Ошибка интегрирования на одном шаге (локальная ошибка)

определяется по формуле

М = (—42&

- 224^3 —

21&4

+ 162£

+ 125б

), (17.20)

где

= Дxf ^Xj + ДА:, у; + (7^ + Ю6

+ FC

) j;

= Дxf j xj + -у Дх, ^ + -ggg- (28*! — 125*

+ 546£

+ 54*4 — 378*

) j.

Применяя (17.19) к решению интегралов (17.5), получим рабо-

чие формулы

где

= В

+ (Д В

+ 4Д В

+ Д В

);

= Li + 4 (ALi + 4AL

+ Д£

);

= Л

+ -g- (ДЛ

+ 4ДЛ

+ ДЛ

= 5

cos «j,

sin a;

ДЛ^ =

ALj

sin

Ф1,

(17.21)

(17.22)

V,=

l+0,6

Vi = Pcos

Ф,; = = 0,0322304 S;

l+0,2

P = 1,25e'

, i = 1,..., 6 — номер пробного шага.

Для эллипсоида Красовского

С = 6399 698,9 м, р = 0,0084 2316.

Значения сн и ф* приведены в табл. 153.

Локальные ошибки для координат и азимута вычисляются по

формулам

Мдя = (—42A£

— 224Д£

— 21Д£

+ 162Д£

+ 125Д£

);

Мъь = -355- (—42AL

— 224AL

— 21AL

+ 162AL

+ 125AL

);

• (17.23)

336

(—42ДЛ

— 224ДЛ

—

21ДЛ

-г 162ДЛ

+ 125ДЛ

281;

Таблица

187

Л 4

0,5АЛ i

А1

+ 0,25 (ДЛ1+АЛ

)

Ai—ДЛ2+2ДЛ3

AI+ -(7АЛ1 + ЮАЛ

+АЛЗ)

А1

*/б25

(28АЛ 1— 125АЛ

+ 546АЛ

+ 54 АЛ 4—378АЛ

)

В!

0.5ABJ

Bi+0,25 (ABi+ДВ

)

Вх—АВ

+2АВ

Bi+ -(7ASi + 10AB

+AS

)

+ V

625

(28ABi—125A£

+ 546A Я

+ 54AB

—378A£

)

Точностная характеристика метода Рунге—Кутта — Ингланда,

выполненная моделированием на ЭВМ для различных координат

и расстояний, приведена в табл. 154.

Таблица 154

Широта

Расстояние, км

Погрешности

<65°

S<300

Мдв <0,1—0,15 м

Мм <0,1—0,15 м

Мдл <0,003"

<65°

5 <500

Мь

<0,3—0,7 м

Мм <0,3—0,7 м

дл

<0,03—0,04"

75°<В<80°

S<100

МАВ <0,1 м

Mal <0,1 м

Мал <0,003"

75°<В<80°

S<200

МАВ <1,6 М

MAL <1,6 М

МАЛ <0,3"

Таблица составлена на основании результатов вычислений при

однократном шаге интегрирования =

Формула (17.20) локальной ошибки интегрирования М позво-

ляет при использовании ЭВМ применить автоматическое измене-

ние шага в процессе интегрирования. При некоторой заданной

ошибке интегрирования г на одном шаге схема такого изменения

может быть следующей:

A xj

J+1

A xj,

2Axj,

если Mi > е;

если Mi = е;

если M

< е,

282

где Д*/+1 — величина шага интегрирования из точки (xj+\, yj+i),

если ТИ^в, или из точки (я/, *//), если М>г; i= 1, ..., п — номер

шага.

Реализация схемы автоматического выбора шага на 20—30%

сокращает время, необходимое для получения решения, по срав-

нению с методом интегрирования при постоянном шаге.

Схема решения

Формулы

4 1

9 065,125

а.

3°29'45,83"

3°35'17,18" 3°35'29,34" 3°41'38,52" 3°37'27,47"

3°32'00,33"

50 07 40,97

51 23 23,91

51 23 23,18

52 39 03,89

51 48 37,04

50 37 58,02

cos а.

0,9981390

0,9980398

0,9980362 0,9979226

0,9980001

0,9980992

sin а.

0,0609800

0,0825833

0,0626421

0,0642283

0,0632137

0,0616308

COS

0,6410740

0,6240162

0,6240191

0,6066674

0,6182672

0,6342883

sin ф.

0,7674791

0,7814114

0,7814091

0,7949558 0,7859679

0,7730966

COS2 ф.

0,4109759

0,3893962

0,3893998

0,3680453

0,3822543

0,4023216

0,0034617

0,003 2719

0,0032800 0,0031001 0,0032198

0,0033888

1+0,6 у.

1,002077

1,001968

1,001968 1,001860 1,001931

1,002033

1+0,2 у.

1,000692

1,000656

1,000656 1,000620 1,000644 1,000677

1,001384

1,001311 1,001311

1,001239 1,001287

1,001355

1,004157

1,003933

1,003938 1,003721

1,003866 1,004071

sin a./cos ф.

0,0951216

0,1002911 0,1003849

0,1062003

0,1022433

0,0971653

AB",

9085,87" 9082,98"

9082,95"

9079,96" 9081,97"

9084,73"

д ВО.

AL".

AL0.

2°ЗГ25,87"

2°31'22,98"

2°31 '22,95"

2°31'19,96"

2°31 '21,97

2°31'24,73"

д ВО.

AL".

AL0.

863,48"

910,34"

911,19"

963,91"

928,04"

882,01"

д ВО.

AL".

AL0.

0°14'23,48"

0°15'Ю,34"

0°15'11,19"

0°16'03,91"

0°15'28,04"

0°14'42,01"

Д Л".

662,70" 711,35"

712,02"

766,27"

729,41"

681,83'

ДД0.

0°11'02,70"

0° 11' 51,35"

0°11'52,02" 0°12'46,27"

0°12'09,41"

0°11 '21,88"

Д Я= — (9085,87" + 4- 9082,95" + 9079,96") = 9082,94" = 2°ЗГ22,94"

AL = — (863,48" + 4-911,19" + 963,91") = 912,02" = 0°15' 12,02"

ДЛ= — (662,70" + 4-712,02" + 766,27") = 712,84" = 0°1Г52,84"

= B

+ ДВ = 50°07'40,97" + 2°ЗГ22,94" = 52°39'03,91"

= L

+ M=- 23°45'13,43" + 0°15'12,02" = 24°00

25,45"

= A

+ А± 180° = 3°29'45,83" + 0°1Г52,84" = 183°41'38,67"

М^в = 1/336(^381 606,5"—2034 580"—190 679,1"+1 471 279"+1 135 591")

=4,4"/336=0,013"

M^l =

/336(—36266,16"—204 106,5"—20 242,11"+150 342,4"+110 251,2")

= —21,2"/336 = —0,063"

/336( — 27 833,40"—159 492,4"—16 091,67"+118 164,4"+85 235,0") =

= — 18,17336= —0,054"

283;

Пример 12. По геодезическим координатам начальной точки

В\, L

прямому азимуту A\

и расстоянию S вычислить геодезиче-

ские координаты конечной точки В

, Ь

и обратный азимут А

пользуясь формулами (17.21), (17.22) и табл. 153. Выполнить

оценку точности решения по формулам (17.23).

Исходные данные

=Ai

50° 07' 40,97"

23 45 13,43

3 29 45,83

281260,08 м

0,00842316

§ 89. Решение обратной геодезической задачи по формулам

со средними аргументами (способ Гаусса)

Способ Гаусса основан на разложении подынтегральных функ-

ций (17.5) в ряд Тейлора по средним аргументам, которыми яв-

ляются:

+ В

Lfn —

— "

180°

Разложение по средним аргументам приводит к выражениям

(17.6), в которых члены, содержащие четные степени производ-

ных, обращаются в нуль. Новые

ряды лучше сходятся и имеют

^21 более компактный вид.

Особенность метода Гаусса

Qzl

z) заключается в следующем.

I j Пусть точка С с координата-

I ми В о, Lo и азимутом в ней Ао

РИС< 71

делит геодезическую линию S

(рис. 71) пополам.

Для разностей (В

{

—Во) и (В

—Во) можно получить ряды:

I dB \ S 1 ( d*B \

1 / d

B \ _

(Bl

- ад = - - + - (ж s

Л v

( dB \ S 1 / d

B \ 1 / d

B \

оо

*о)

= - + X

+ Ж" (-35Г)

Вычитая первое уравнение из второго, получим

/ dB \ 1 / d

B \

Аналогичным образом получим:

(

dA \ 1 / d

A \

(17.24)

(17.25)

В выражениях (17.25) и (17.24) частные производные берутся

по координатам В

, L

Ао точки С. Однако средние аргументы

284;

, L

, Am соответствуют точкам геодезической линии S

, L

(см. рис. 71), не совпадающими с точкой С. Поэтому в (17.24) и

(17.25) необходимо ввести поправки за разности (В

—В

), (L

—

—L

) и {Am—Л

). Практические (17.24) и (17.25) необходимо сде-

лать переход от частных производных (dB/dS)

к частным произ-

водным вида (dB/dS)

. Такой переход можно сделать на основа-

нии известной связи, которая, например для широты, имеет вид

( dB \ _ j dB \ \ dS )

dS2

)т

Аналогичные уравнения связи частных производных можно по-

лучить для долготы и азимута. Несложные преобразования, свя-

занные с подстановкой выражений типа (17.26) в (17.24) и

(17.25), а также выражений для частных производных (dB/dS)

(dLJdS)m, (dA/dS)

т разных порядков, приводят к следующим ра-

бочим формулам:

5 sin А

= D [aj + а

АВ

Г+ = D2j, (17.27)

cos Am

[a^AB

+ а

дБ/» + а

Д£

] = D2

, (17.28)

ДA

= sin B

[a~7+

Д£

7+ =

in £

, (17.29)

где

m = 593,602 160; AB =

— B

•

10"

;

n= 197,867 385; 7= (L

—

LJ'-10~

;

+ cos

n +

COS

Bm '

103

422,05 cos B

;

= 9,5144

cos

+ 0,5525 cos

— 0,0078 cos

;

= —10,1287 cos B

+ 10,1287

cos

;

103

422,05

—

696,9116 cos

+ 4,6954 cos

—

0,0310

cos

;

= —30,3860 + 10,3334 cos

— 0,2061

cos

+ 0,0014 cos

;

= —0,2048 +0,4192 cos

- 0,0124 cos

10 000

= 10

;

= 2,9381 + 0,0132 cos

1,9587

cos

+ 0,0132 cos

Из формул (17.27), (17.28), (17.29) получим искомое решение

обратной геодезической задачи:

v. х

i о S, + s

A—anrtg-jJ-; S^-^fa; =

= A

—~AA; A

± +

285;

Формулы (17.27), (17.28), (17.29) обеспечивают вычисление

расстояния S с ошибкой 5—10 см и азимута с ошибкой 0,05 " при

решении обратной геодезической задачи на средние расстояния.

Значения cos В

для вычисления а\ нужно брать с семью де-

сятичными знаками, значение cos В

для а

— с шестью десятич-

ными знаками. Значения cos В

для остальных коэффициентов а

достаточно брать с четырьмя десятичными знаками.

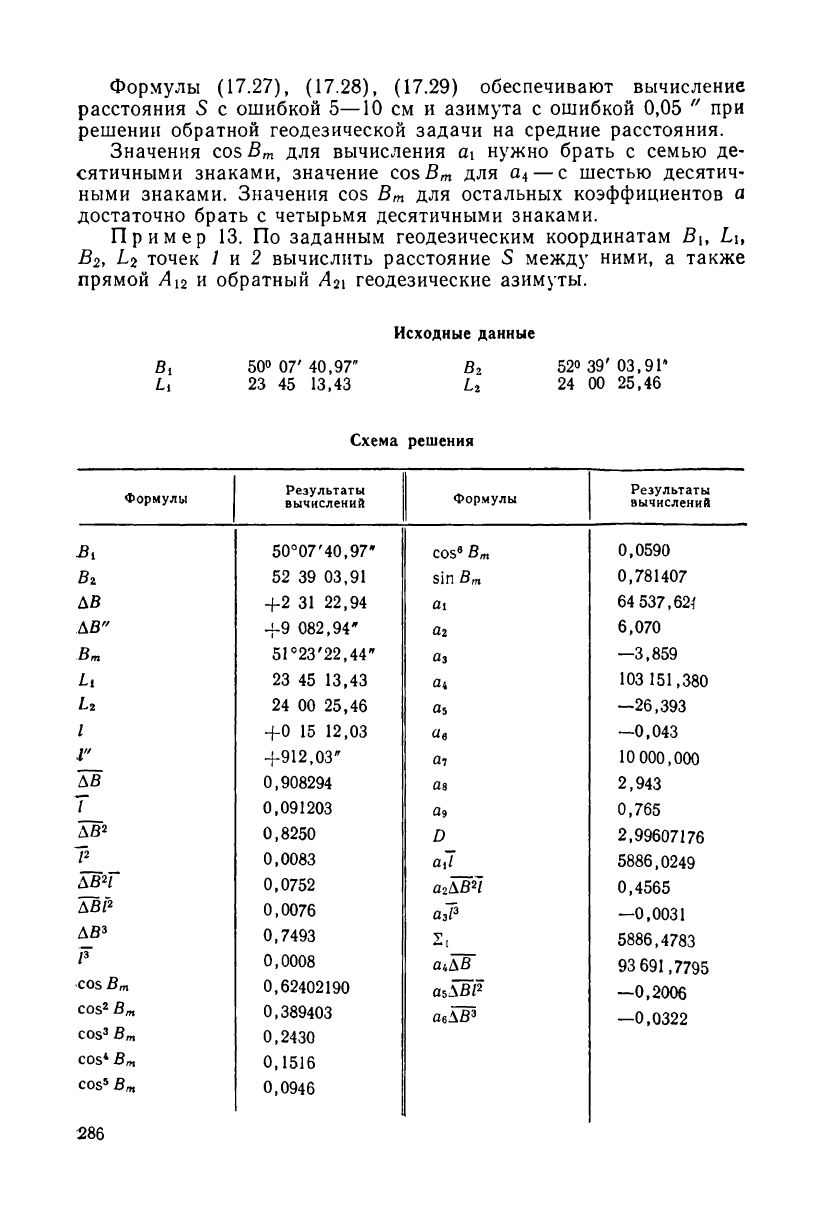
Пример 13. По заданным геодезическим координатам В

Li,

у L2 точек / и 2 вычислить расстояние 5 между ними, а также

прямой А12 и обратный Л21 геодезические азимуты.

Исходные данные

BI 50° 07' 40,97" В

52° 39' 03,9Г

U 23 45 13,43 U 24 00 25,46

Схема решения

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

В!

50°07'40,97*

cos

0,0590

Вг

52 39 03,91

sin B

0,781407

д в

+2 31 22,94

64 537,624

АВ"

4-9 082,94"

6,070

Вт

51°23'22,44"

—3,859

23 45 13,43

103 151,380

24 00 25,46

—26,393

+0 15 12,03

—0,043

+912,03"

000,000

АВ

0,908294

as 2,943

0,091203

0,765

АВ

0,8250

2,99607176

0,0083

5886,0249

двч

0,0752

агАВЧ

0,4565

АВ1

0,0076

—0,0031

А Я

0,7493

5886,4783

0,0008

691,7795

cos B

0,62402190

аьАВР

—0,2006

cos

0,389403

аьАВ*

—0,0322

cos

0,2430

—0,0322

cos

0,1516

cos

0,0946

286;

Формулы

Результаты

вычислений

Формулы

Результаты

вычислений

+93 691,5467

912,0300

cos A

281 260,08 м

а%АВ*Г

0,2213

tScp

281 260,08 м

0,0006

Д Л:

= sin B

2з

+712,84"

Тз

912,2519

АЛ

11'52,84*

S sin Am^DZt

S cos Л

= 02г

17 636,312

280 706,597

ДЛ

5'56,42"

0,06282828

3°35'42,25"

3°29

45,83

,г

sin

0,06270464

=Л

±180° +

183°41'38,67*

Cos Am

sin A

0,99803213

281 260,08 м

§ 90. Решение главных геодезических задач

при больших расстояниях между пунктами:

Метод Рунге — Кутта — Ингланда дает возможность решать

прямую геодезическую задачу на любые расстояния. Действитель-

но, любое большое расстояние можно разделить на части, кото-

рые соответствуют, например, средним расстояниям, и применить

метод Рунге — Кутта — Ингланда к каждой части в отдельности.

При этом каждую часть большого расстояния можно рассматри-

вать как шаг интегрирования. Во многих случаях решение пря-

мой геодезической задачи на большие расстояния требуется полу-

чить с точностью порядка 1—2". Это обстоятельство дает возмож-

ность выбирать шаг интегрирования длиной до 1000 км и в конеч-

ном итоге получить оптимальный метод решения, техническая сто-

рона которого не отличается от изложенного в § 88.

Более сложным является решение обратной геодезической за-

дачи на большие расстояния. Все существующие методы решения

этой задачи базируются на идее Бесселя, но необходимо наилуч-

шим образом выполнить аппроксимацию исходной подынтеграль-

ной функции. В настоящее время наилучшей аппроксимацией, па

нашему мнению, является аппроксимация дробно-рациональным,

выражением с помощью цепных дробей.

Рассмотрим более подробно идею и алгоритм решения обрат-

ной геодезической задачи, построенной на ее основе.

Длину геодезической линии 5 между пунктами Qi и Q

можно»

представить с помощью выражения

Ф2 Ф1

Ут

287;

где k

= e

sin

\ е

первый эксцентриситет референц-

эллипсоида, a, b — полуоси референц-эллипсоида.

. j sin

cos

У, /17

о j \

С' _ .

о —

т sin

—

sin

fy cosy/ coscpj „

= —w^HQ—^yi-*

' '-

(l7<32)

— широта точки Qm экстремума геодезической линии; W

= тр,

^ * т

Nт — радиус кривизны первого вертикала в точке экстремума.

Интегралы в (17.30) выражают длины дуг геодезической линии

от точки экстремума Q

до точки с широтой Bi.

Если в (17.30) подынтегральные функции представить дробно-

рациональными выражениями [1], получим

^ [о,2 (ф

Ф1

) + «ч - «4

(17

33)

где ai = arc tg ()

1 — 1

>25k

ф|

), t = 1, 2. (17.34)

Азимуты геодезической линии в точках Q\ и Q2 определяются

на основании теоремы Клеро по формулам

• ^

cos

. ,,

— -

VmCosBi

. (17.35)

• ^

S Vm

/17 9A>

sin (17.36)

Формулы (17.33), (17.35), (17.36) в общем виде решают об-

ратную геодезическую задачу. Однако результат решения суще-

ственно зависит от взаимного расположения исходных точек Qь

и точки экстремума Q

с - ^

1 ^ ^ j

РИС. 72 РИС. 73 РИС. 74

Взаимное расположение этих точек практически исчерпывается

следующими тремя случаями, изображенными соответственно на

рис. 72—74.

Имея в виду соображения, положенные в основу вывода фор-

мул (17.30) и (17.33), нетрудно заметить, что в первом случае

(см. рис. 72)

| , (17.37)

т. е. искомое расстояние вычисляется по формуле (17.33).

288