Яковлев В.В. Экологическая безопасность, оценка риска
Подождите немного. Документ загружается.


81
• социальный риск – зависимость частоты событий, в которых по-
страдало число людей больше определенного значения.
Анализ интенсивности возникновения опасностей производится
на основе обработки статистических данных об авариях на объектах опре-
деленной отрасли (идентичных технологических процессах, видах транс-
порта и т.д.), иди экспертным путем.
В табл. 6.1.1. приведены средние значения интенсивностей возник
-
новения аварийных ситуаций в системе обеспечения нефтепродуктами на
различных этапах обращения.
Таблица 6.1.1
Характерные интенсивности возникновения аварийных ситуаций в
процессе обращения нефтепродуктов.
Вид деятельности
Вид источника опасности
Диапазон средних ин-
тенсивностей аварий,
1/год
Транспортировка Автомобильный транспорт 10
-8
- 10
-5
Водный транспорт 10
-9
- 10
-3
Железнодорожный транспорт 10
-6
- 10
-5
Трубопроводный транспорт 10
-7
- 10
-4
Хранение 10
-7
- 10
-5
Переработка 10
-6
- 10
-5
Анализ возможных последствий производится на основе прогноза
приемлемой степени риска, определяемой:
- законодательством по промышленной безопасности;
- правилами и нормами безопасности;
- сведениями об имеющихся аварийных событиях и их последствиях;
- опытом практической деятельности.
Приемлемым риском называют такой риск, уровень которого допус-
тим и обоснован, исходя из экономических, экологических и социальных
соображений.
Для
ориентировки можно опираться на величины фоновых значений
риска, а также на обобщенные данные общественного мнения, приведен-
ные в табл. 6.1.2, 6.1.3 и 6.1.4.
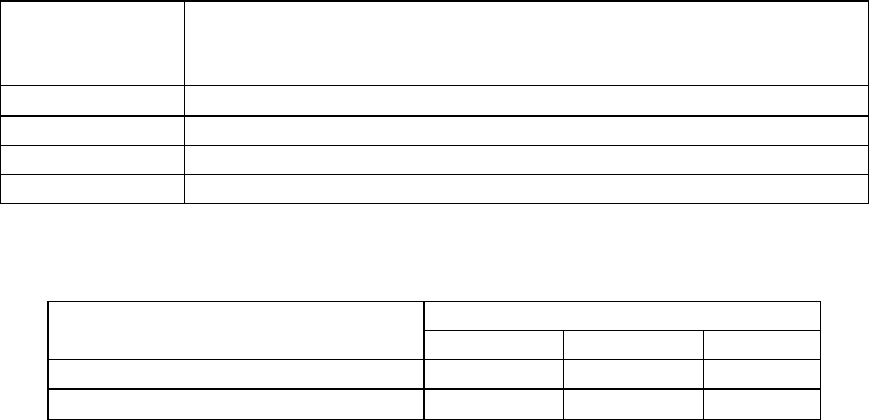
Таблица 6.1.2
Величины фонового риска для населения.
Степень и причина поражения
Страна
Заболевание
и гибель от
болезни
Гибель от
несчастных
случаев
Гибель от социальных
стрессов
Россия (средние значения)
1,1⋅10
-2
8⋅10
-4
- 10
-3
2⋅10
-4
Другие страны (средние
значения)
10
-2
10
-3
(США)
5⋅10
-6
Экстремальные значения
1,5⋅10
-2
4⋅10
-3
5,8⋅10
-4
82
Таблица 6.1.3
Величины риска и ответные реакции общества.
Величина ин-
дивидуального
риска в год
Ответная реакция сообщества
≥ 10
-3
Немедленно принимаются меры по уменьшению опасности
~ 10
-4
Принимаются предупреждающие действия
~ 10
-5
Ведется разъяснительная работа
~ 10
-6
Не слишком волнует «среднего» человека
Таблица 6.1.4.
Величина пренебрежимого и предельно допустимого рисков.
Страны
Уровни риска
США Европа Россия
Пренебрежимый риск 10
-9
- 10
-8
10
-8
10
-6
Предельно допустимый риск 10
-7
- 10
-6
10
-6
5⋅10
-4
ГОСТ Р 12.3.047-98, а также НПБ 105-03 определяющие требования
по пожарной и взрывобезопасности технологических процессов, дают
следующие определения:
индивидуальный риск - вероятность (частота) возникновения опасных
факторов пожара и взрыва, возникающая при аварии в определенной точке
пространства. Характеризует распределение риска.
социальный риск - зависимость вероятности (частоты) возникновения
событий, состоящих в поражении определенного числа людей,
подверг-
шихся поражающим воздействиям пожара и взрыва, от числа этих людей.
Социальный риск характеризует масштаб пожаровзрывоопасности. (Оце-
нивается по поражению не менее 10 человек).
Пожарная безопасность технологических процессов считается безус-
ловно выполненной, если:
- индивидуальный риск меньше 10
-8
;
- социальный риск меньше 10
-7
.
Эксплуатация технологических процессов является недопустимой,
если индивидуальный риск больше 10
-6
или социальный риск больше 10
-5
.
Эксплуатация технологических процессов при промежуточных зна-
чениях риска может быть допущена после проведения дополнительного
обоснования, в котором будет показано, что предприняты все возможные и
достаточные меры для уменьшения пожарной опасности.
После идентификации опасностей переходят к этапу оценки риска.
6.2. Оценка риска.
На этапе оценки риска выявленные опасности должны быть оценены
с точки зрения их соответствия критериям приемлемого риска.

83
Различают качественную и количественную оценку риска.
Задачей качественного анализа риска является определение зон при-
емлемости или неприемлемости риска, а также определение необходимо-
сти проведения количественной его оценки.
Количественный анализ риска подразумевает вычисление значения
риска в конкретной ситуации.
Следует отметить, что проведение сложных и дорогостоящих рас-
четных процедур, точность которых для большинства
технологических
процессов невелика, бывает неоправданной. Погрешность значений веро-
ятностных оценок риска даже при наличии достаточной информации, как
правило, не менее одного порядка. Поэтому на практике в первую очередь
следует применять качественные методы анализа риска.
При разработке мер снижения риска определяющим является сле-
дующий подход.
Во всех случаях, где это возможно,
меры снижения вероятности
аварии должны иметь приоритет над мерами уменьшения последствий
аварии, снижения ожидаемого ущерба.
При анализе риска необходимо выделять четыре характерные груп-
пы, которым может быть нанесен ущерб от аварии:
• персонал объекта;
• население;
• окружающая природная среда;
• материальные ценности.
6.2.1. Качественные методы анализа риска.
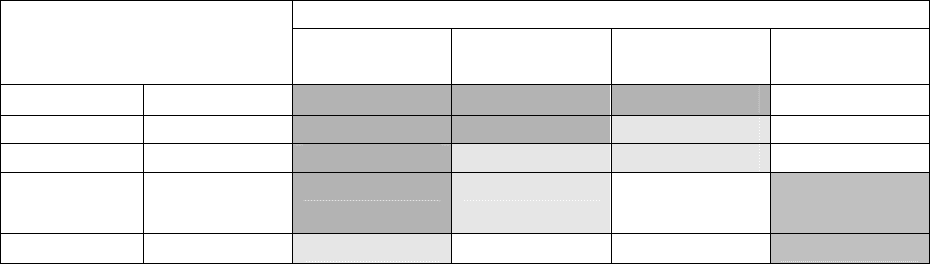
Таблица 6.2.1.1.
Рекомендации
по выбору методов анализа риска.
Вид деятельности
Методы
Разме-
щение
Ввод
(вывод)
в экс-
плуата-
цию
Проек-
тирова-
ние
Экс-
плуата-
ция
Рекон-
струк-
ция
Проверочного листа 0 + + ++ +
Анализ опасности и работоспо-
собности
0 + ++ + ++
Анализ вида и последствий от-
казов
0 + ++ + ++
Анализ дерева событий 0 + ++ + ++
Количественные методы ++ 0 ++ + ++
Среди методов качественного анализа риска наибольшую популяр-
ность имеют:
• метод проверочного листа (что будет, если…?);
84
• анализ вида и последствий отказов;
• анализ опасности и работоспособности;
• анализ дерева отказов;
Рекомендации по выбору метода риск-анализа на различных этапах
проектирования и эксплуатации объекта приведены в табл. 6.2.1.1.В табл.
6.2.1.1 приняты следующие обозначения:
0 – наименее подходящий метод;
+ - рекомендуемый метод;
++ - наиболее подходящий метод.
Естественно, в практике качественной оценки
риска приведенные в
табл. 6.2.1.1. рекомендации выдерживаются редко и используются наибо-
лее приемлемые методы, исходя из объема предоставленной информации,
квалификации исполнителей и выделенных средств.
Метод проверочного листа предполагает в результате составление
перечня вопросов и ответов о соответствии объекта (технологического
процесса) требованиям безопасности и указания по их обеспечению.
Анализ вида и последствий
отказов применяется для качественной
оценки безопасности технических систем. Результаты анализа представ-
ляются в виде таблиц с перечнем оборудования, причин отказов, их часто-
ты, а также с указанием средств контроля и повышения надежности.
В методе анализа опасностей и работоспособности исследуется
влияние отклонений технологических параметров (температуры, давления,
влажности и т.д.) от регламентированных
режимов с точки зрения возник-
новения опасностей.
В табл. 6.2.1.2 приведены рекомендуемые показатели (индексы)
уровня и критичности по вероятности и тяжести последствий отказов (со-
бытий).
Таблица 6.2.1.2
Матрица «вероятность – тяжесть последствий».
Тяжесть последствий Ожидаемая интенсив-
ность возникновения
(1/год)
Катастрофи-
ческая
Критическая Некритиче-
ская
Пренебре-
жимая
Часто
≥ 1
А А А
С
Вероятно 1…10
-2
А А
В С
Возможно 10
-2
…10
-4
А
В В С
Редко 10
-4
…10
-6
А
В С
Д
Невероятно
≤ 10
-6
В С С
Д
В табл. 6.2.1.2. выбраны следующие качественные критерии риска:
• катастрофический – приводит к смерти людей, наносит сущест-
венный ущерб материальным ценностям и невосполнимый ущерб
окружающей природной среде;
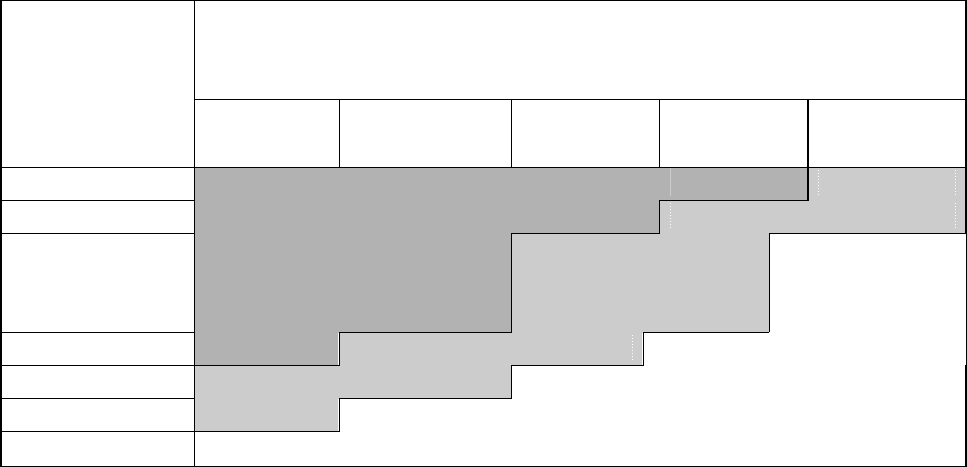
85
• критический (некритический) – угрожает (не угрожает) жизни лю-
дей, потере материальных ценностей, нанесения невосполнимого
ущерба окружающей природной среде;
• с пренебрежимо малыми последствиями – не относящимися по
ущербу ни к одному из первых трех критериев.
Категории областей распределения рассматриваемого пространства
по степени риска:
А – обязателен детальный анализ риска, требуются особые меры
безопасности для его снижения;
В – желателен детальный анализ риска, требуются меры обеспечения
безопасности;
С – рекомендуется проведение анализа риска и принятие мер безо-
пасности;
D – анализ риска и принятие мер повышения безопасности не требу-
ются.
По аналогии с табл. 6.2.1.2 составлены матрицы определения опас-
ности территориальных зон по критерию финансового ущерба (табл.
6.2.1.3) и
по критерию социальных потерь (табл. 6.2.1.4).
Таблица 6.2.1.3.
Матрица для определения опасности территорий (зон) по критерию
“частота реализации - финансовый ущерб”.
Финансовый ущерб, МРОТ
Интенсивность
реализации
опасности,
случаев/год
> 200000 20000-200000 2000-20000 200-2000 <200
> 1
Зона
1 – 10
-1
Зона неприемлемого риска,
жесткого контроля,
10
-1
– 10
-2
необходимы неотложные
меры по снижению
риска
необходима оценка
целесообразности мер
по снижению
10
-2
– 10
-3
риска
Зона
приемлемого
риска,
10
-3
– 10
-4
нет необходимости в
10
-4
– 10
-5
мероприятиях по снижению риска
10
-5
– 10
-6
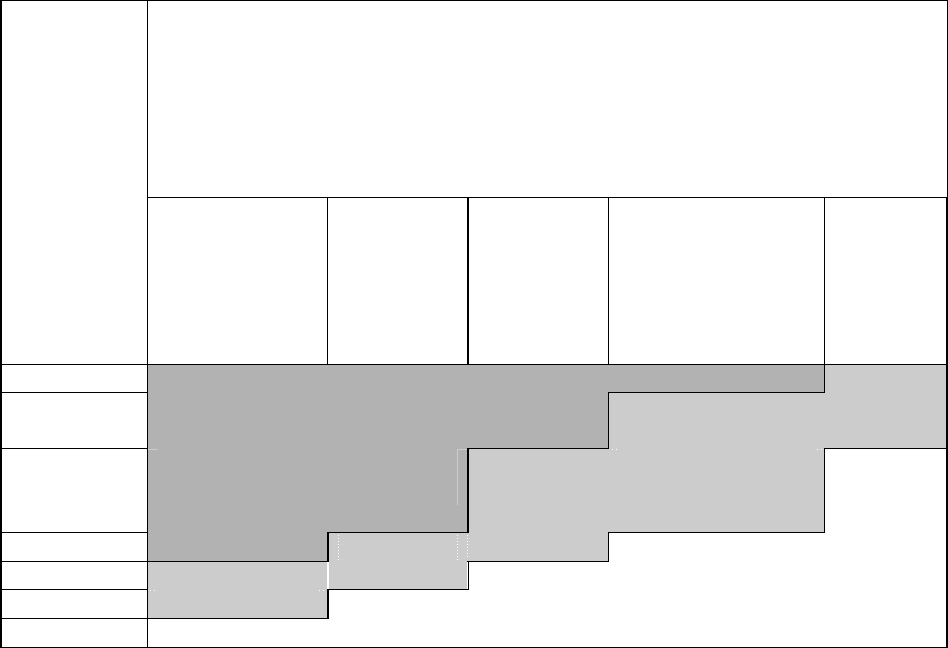
86
Таблица 6.2.1.4.
Матрица определения опасности территорий (зон) по критерию “частота
реализации – социальный ущерб”.
Социальный ущерб
Интенсив-
ность
реализации
опасности,
случаев/год
Погибло более
одного
человека,
имеются по-
страдавшие
Погиб
один
человек,
имеются
постра-
давшие
Погибших
нет,
имеются
серьезно
постра-
давшие
Серьезно
пострадавших
нет, имеются
потери
трудоспособности
Лиц с
потерей
трудо-
способ-
ности
нет
> 1
Зона
1 – 10
-1
Зона неприемлемого риска,
необходимы неотложные меры
жесткого
необходима
контро-
ля
10
-1
– 10
-2
по уменьшению риска
Оцен-
ка
мер
целесообразности
по уменьшению
Зона
10
-2
– 10
-3
риска
приемлемого риска,
10
-3
– 10
-4
нет необходимости в
10
-4
– 10
-5
мероприятиях по уменьшению риска
10
-5
– 10
-6
6.2.2. Количественные методы оценки риска.
Выбор уровней приемлемого риска в техногенной сфере может бази-
роваться на следующих основополагающих принципах:
- невозможность обеспечения абсолютной безопасности (нулевого
риска) независимо от рассматриваемой аварийной ситуации;
- введение предельно допустимого уровня риска, выше которого
риск признается абсолютно недопустимым, и одновременное вве-
дение пренебрежимо малого уровня
риска, ниже которого про-
блемами борьбы с опасностью можно пренебрегать.
В мультипликативном подходе мера риска R определяется как
свертка (зачастую – произведение) вероятности W реализации аварии и ве-
роятного относительного ущерба M по формуле:
MWR ⋅=
(6.2.2.1)
где R – количественная мера (степень) риска;
W - вероятность возникновения аварии;
М - вероятный относительный ущерб при аварии.
87
Значение риска в мультипликативном представлении можно тракто-
вать как математическое ожидание ущерба.
Вероятность W возникновения аварии определяется на основе анали-
за условий эксплуатации объекта или технической системы и обработки
статистических данных об авариях.
В простейшем представлении можно воспользоваться законом Пуас-
сона распределения времени между авариями, полагая, что наступления
аварий образуют простейший поток
случайных событий.
Как известно, при таком подходе вероятность Р(N, t) появления ров-
но N аварий за время t рассчитывается по среднему значению λ интенсив-
ности возникновения аварийных ситуаций:
()
()
0...,2,1,0,exp
!
),( >⋅=⋅−⋅
⋅
= tNt
N
t
tNP
N
λλ
λ
(6.2.2.2)
Из (6.2.2.2) следует, что в течение времени t ни одной аварии не про-
изойдет с вероятностью Р(0, t):
(
)
ttP ⋅−=
λ
exp),0(
(6.2.2.3)
Вероятность P(1, t) того, что за время t произойдет ровно одна ава-
рия:
()
tttP ⋅−
⋅
⋅=
λ
λ
exp),1(
(6.2.2.4)
Вероятность того, что за это время произойдет хотя бы одна авария
(одна или более):
(
)
WttPtP
=
⋅
−
−=−=≥
λ
exp1),0(1),1(
(6.2.2.5)
Последняя вероятность и принимается как мера риска возникновения
аварии на рассматриваемом объекте за интересующий интервал времени t.
Пример 6.2.2.1.
Пусть установлено, что на объекте аварийная ситуация с выходом
метана происходит в среднем 2 раза в течение 50 лет.
Требуется определить вероятность возникновения одной аварии в
течение ближайших 10 лет, а также оценить меру риска возникновения
аварийных ситуаций за это же время в предположении о том, что появле-
ние аварий подчинено простейшему потоку случайных событий.
Решение.
Интенсивность возникновения аварийных ситуаций:
год
1
04.0
50
2
==
λ
Вероятность возникновения за 10 лет ровно одной аварии:
()
268.0)1004.0exp(1004.0exp),1(
=
⋅
−
⋅
⋅
=
⋅−
⋅
⋅= tttP
λ
λ
Вероятность того, что за 10 лет не произойдет ни одной аварии:
(
)
67.0)1004.0exp(exp),0(
=
⋅
−
=⋅
−
= ttP
λ
Риск возникновения аварии за 10 лет (вероятность того, что про-
изойдет хоть одна авария с выходом метана):

88
(
)
33.067.01exp1),0(1),1(
=
−
=
⋅
−
−
=
−
=
≥= ttPtPW
λ
Таким образом, в инженерных оценках может быть рассчитана веро-
ятность W возникновения аварии.
Вероятный относительный ущерб М рассчитывается по следующей
методике.
На основе моделирования аварийной ситуации прогнозируются ма-
териальные M
v
и людские N
v
потери
вследствие воздействия формируе-
мых в аварии поражающих факторов.
По таблице 6.2.2.1 определяется вид чрезвычайной ситуации и соот-
ветствующие максимальные значения возможного материального ущерба
М
max
или гибели людей N
max
. Тогда:
max
M
M
M
V
m
=
, (6.2.2.6)
или
max
N
N
M
V
n
=
(6.2.2.7)
где M
m
и M
n
– вероятный относительный материальный и людской
ущербы соответственно.
Возникает естественный вопрос об определении вероятного относи-
тельного ущерба в случае, когда в одной аварийной ситуации гибнут люди
и наносится материальный ущерб, например, в виде разрушенных (сго-
ревших) корпусов или потери иных ценностей объекта.
В этом случае можно воспользоваться так называемой стоимостью
жизни,
принимаемой в среднем по цивилизованным странам в размере
120000 долларов. При аварии подводной лодки «Курск» (август 2000 г.)
правительство РФ выплачивало компенсацию семьям погибших моряков в
размере примерно 700000 руб., а семьям погибших в результате террори-
стического акта в Москве (октябрь 2002г.) компенсация составила 100000
руб. В проекте «Методических рекомендаций по оценке ущерба от
аварий
на опасных производственных объектах» [15] несчастный случай со смер-
тельным исходом взрослого человека оценивается суммой 80 000 руб.
Тогда окончательно получаем:
maxmax
NgMk
NgMk
M
vv
⋅+⋅
⋅+⋅
=
, (6.2.2.8)
где коэффициент k приводит к единой мере финансовые единицы
измерения ущербов, например, МРОТ и доллары;
коэффициент g равен выбранной мере стоимости жизни одного
человека в единицах, соответствующих единицам ущерба.
Пример 6.2.2.2.
Пусть в рамках исходных данных примера 6.2.2.1 прогнозируется
гибель 7 человек и нанесенный материальный ущерб в размере 800 МРОТ,

89
т.е. рассматриваемая чрезвычайная ситуация относится к классу локаль-
ных. Стоимость жизни человека принимаем равной 120000 долларов.
Воспользуемся данными табл. 6.2.2.1 по классификации чрезвычай-
ных ситуаций в соответствии с Постановлением Правительства РФ.
Таблица 6.2.2.1.
Классификация чрезвычайных ситуаций.
(Постановление Правительства РФ от 13.9.96 №1094).
Нанесенный ущерб
Чрезвычай-
ная ситуация
Пределы зоны
распростране-
ния ЧС
Число
постра-
давших,
чел
Нарушены
условия
жизнедея-
тельности,
чел
Матери-
альный
ущерб,
МРОТ
Силы
ликвида-
ции
послед-
ствий
Локальная Объект До 10 100 1000 Органи-
зации
Местная Населенный
пункт
10…50 100…300 10
3
…10
5
Местного
само-
управле-
ния
Территори-
альная
Субъект РФ 50…500 300…500
5⋅10
3
…5⋅10
5
Субъекта
РФ
Региональная Два субъекта
РФ
50…500 500…1000
5⋅10
5
…5⋅10
6
Субъек-
тов РФ
Федеральная Более двух
субъектов РФ
Более 500
Более
1000
Более 5⋅10
6
Субъек-
тов РФ
Трансгранич-
ная
За пределами
гос. границы
РФ
- - - Прави-
тельства
РФ
Из табл. 6.2.2.1 имеем:
М
max
= 1000 МРОТ, N
max
=10 чел.
По исходным данным:
- материальный ущерб = 800 МРОТ,
- потери населения составляют 7 человек.
Принимая 1 МРОТ = 100 руб. ≅ 3.2 доллара, получим из (6.2.2.8) при
k=3.2:
g⋅
8400007120000 =⋅=
v
N
долларов,
k⋅
=⋅= 8002.3
v
M
2560 долларов.
k⋅М
max
= 1000⋅3.2=3200 долларов.
g⋅N
max
= 10 ⋅120000 = 1200000 долларов.
Значение вероятного относительного ущерба М составит:
7.0
1203200
842560
12000003200
2560840000
==
+
+
=M

90
С учетом решения примера 6.2.3.1 получим значение риска в муль-
типликативной форме:
231.07.033.0 =⋅=⋅= MWR
Метод целевой функции предполагает более корректное определение
существа риска. Кроме параметров, участвующих в решении задачи опре-
деления значений риска по мультипликативному критерию, необходима
дополнительная информация о затратах и о потенциальной экономической
(платежной) способности предприятия, региона или лица, ответственного
за принятие решения.
В статической постановке целевая функция риска L(c) рекомендова-
на в
работе [14] в следующем виде:
()
[]
maxmax
10
)()()()(1
)(
NgMk
cWcmNgMk
S
cWc
cL
kvvk
⋅+⋅
⋅
−
⋅
+
⋅
+
−
⋅
=
(6.2.2.9)
где с
0
– затраты на создание технической системы (объекта);
W(c
k
) – вероятность возникновения аварийной ситуации, значе-
ние которой определяется средствами c
k
, затрачиваемыми на предотвра-
щение возникновения аварийной ситуации;
M
v
– прогнозируемый ущерб материальным ценностям и окру-
жающей природной среде;
N
v
– прогнозируемые людские потери в размерности выбранных
финансовых средств;
с
1
– затраты на обеспечение безопасности системы (снижение
ожидаемого ущерба);
c
k
– средства, выделяемые на предотвращение аварий;
k, g – коэффициенты приведения стоимостных показателей
ущерба и потери населения к единой мере;
m(с
1
) – функция предотвращенного ущерба, значение которой
определяется выделяемыми средствами с
1
:
)()()(
1 NvMv
cngcmkcm
⋅
+⋅=
(6.2.2.10)
m
v
(c
M
) – предотвращенный материальный ущерб;
n
v
(c
N
) - предотвращенный ущерб вследствие людских потерь;
NM
ccc
+
=
1
S – потенциальная платежная способность заказчика или лица,
ответственного за принятие решения.
kNM
ccccS ++
+
≥
0
(6.2.2.11)
Вероятность негативного воздействия на среду обитания W(c
k
) мо-
жет быть представлена в виде зависимости от надежности исследуемой
технической системы:
[
]
)(1)()(
yxk
cPcWcW −⋅=
, (6.2.2.12)
где
yxk
ccc
+
=
;
