Yu W., LaBoube R.A. Cold-Formed Steel Design

Подождите немного. Документ загружается.

STRUCTURAL BEHAVIOR OF COMPRESSION ELEMENTS AND DESIGN CRITERIA 65

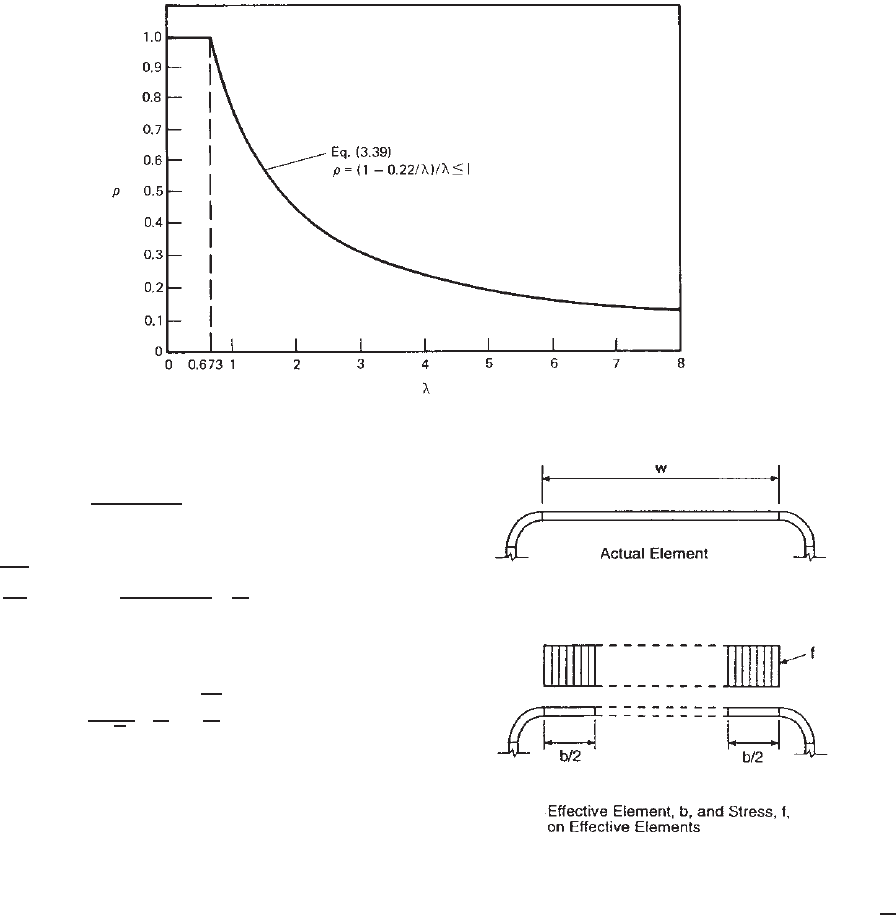
Figure 3.18 Reduction factor ρ vs. slenderness factor λ.

and

ρ =

1 − 0.22/λ

≤ 1 (3.43)

where the plate slenderness factor λ is given as

λ =



kπ

12(1 − μ

)





The above equation for the plate slenderness factor can

be simpliﬁed to Eq. (3.44) by using μ = 0.3:

λ =

1.052

√







(3.44)

where k = plate buckling coefﬁcient

= 4.0 for stiffened elements supported by a web

on each longitudinal edge as shown in

Fig. 3.19. Values for different types of

elements are given in the applicable sections

of the North American Speciﬁcation.

w = width of stiffened compression element

t = thickness of compression element

E = modulus of elasticity

f = maximum compressive edge stress in element

without considering safety factor

Since Eq. (3.44) is a simpler equation than the design proce-

dure prescribed in the North American Speciﬁcation, this

equation is used in this book for computing the slenderness

factor λ.

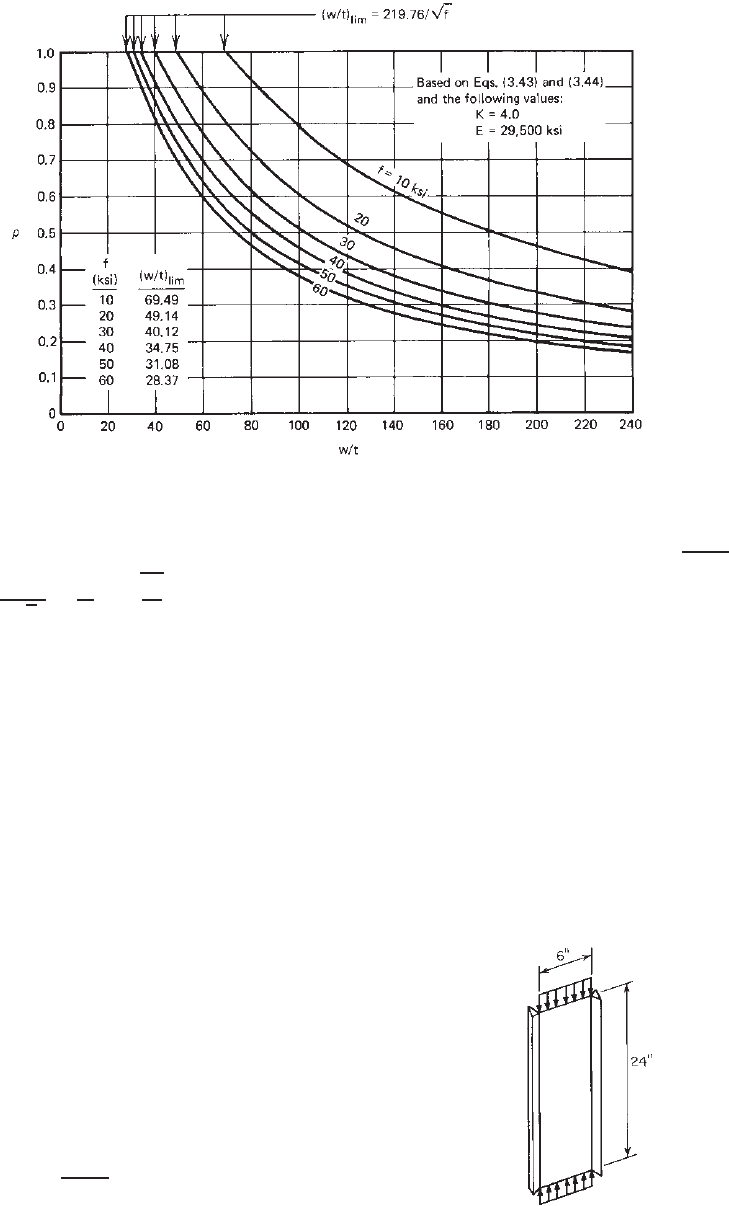
Figure 3.20 is a graphic presentation of Eqs. (3.43) and

(3.44) plotted for k = 4.0 and E = 29,500 ksi. It can be used

for determination of the effective design width of stiffened

elements with a given w/t ratio and compressive stress.

Figure 3.19 Uniformly compressed stiffened elements.

1.345

Note that the limiting w/t ratio, (w/t)

lim

, is 219.76/

√

When w/t ≤ (w/t)

lim

, no reduction of the ﬂat width is

required for stiffened e lements supported by a web on each

longitudinal edge.

(b) Serviceability Determination



w for λ ≤ 0.673 (3.45)

ρw for λ ≥ 0.673 (3.46)

where b

= effective design width of compression

element for serviceability determination

w = ﬂat width of compression element

ρ = reduction factor determined from Eq. (3.43)

66 3 STRENGTH OF THIN ELEMENTS AND DESIGN CRITERIA

Figure 3.20 Reduction factor ρ for stiffened compression elements.

The plate slenderness factor λ is determined as

λ =



1.052

√













(3.47)

where f

is the computed compressive stress in the element

being considered and k , t,andE are the same as that

deﬁned above for strength determination.

The above method [Eqs. (3.45)–(3.47)] can be used to

obtain a conservative effective width b

for serviceability

determination. It is included in Section B2.1(b) of the North

American Speciﬁcation as Procedure I. Figure 3.20 can also

be used for the determination of the effective width for

serviceability using this procedure.

For stiffened compression elements supported by a web

on each longitudinal edge, a study conducted by Weng and

Pekoz indicated that Eqs. (3.48)–(3.51) can yield a more

accurate estimate of the effective width b

for service-

ability. The following equations are included in the North

American Speciﬁcation as Procedure II:

ρ =

⎧

⎪

⎨

⎪

⎩

1forλ ≤ 0.673 (3.48)

(1.358 − 0.461/λ)/λ ≤ 1

for 0.673 <λ<λ

(3.49)

(0.41 + 0.59



− 0.22/λ)/λ ≤ 1

for λ ≥ λ

(3.50)

where

= 0.256 + 0.328(w/t)



/E (3.51)

and λ is deﬁned by Eq. (3.47).

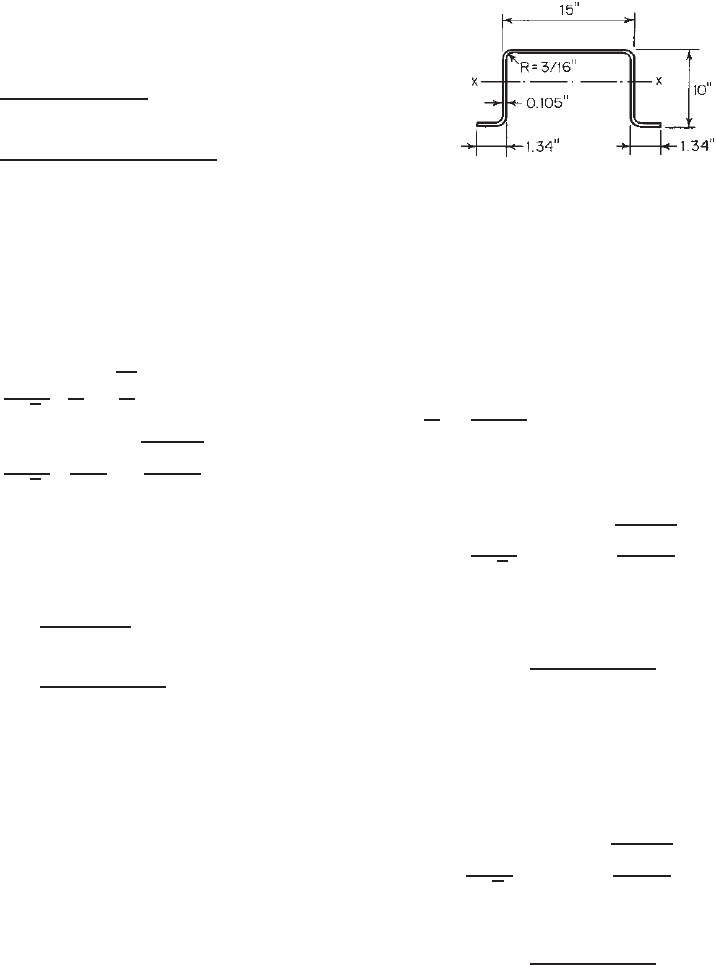
Example 3.1 For the given thin plate supported along

both longitudinal edges as shown in Fig. 3.21, determine

the following items using the U.S. customary unit:

1. Critical buckling stress

2. Critical buckling load

3. Ulitmate load.

Given:

t = 0.06 in. E = 29.5 × 10

ksi F

= 50 ksi

μ = 0.3

Figure 3.21 Example 3.1.

STRUCTURAL BEHAVIOR OF COMPRESSION ELEMENTS AND DESIGN CRITERIA 67

SOLUTION

1. Critical Buckling Stress [Eq. (3.16)]. Since the aspect

ratio is 4, use k = 4.0 as follows:

kπ

12(1 − μ

)(w/t)

4(3.1416)

× (29.5 × 10

)

12(1 − 0.3

)(6/0.06)

= 10.665 ksi

2. Critical Buckling Load. P

= Af

= 6(0.06) ×

(10.665) = 3.839 kips.

3. Ultimate Load. The ultimate load can be computed

from the effective width b determined by Eq. (3.41)

or Eq. (3.42). From Eq. (3.44),

λ =

1.052

√







1.052

√



6.0

0.06





29,500

= 2.166

Since λ>0.673, b = ρw,where

ρ =

1 − 0.22/λ

1 − 0.22/2.166

2.166

= 0.415

Therefore, the effective design width and the ultimate

load are c omputed as follows:

b = ρw = 0.415(6.0) = 2.49 in.

ult

= A

eff

= 2.49(0.06)(50) = 7.47 kips

It is seen that here the ultimate load of 7.47 kips

is almost twice the critical buckling load of

3.839 kips.

Example 3.2 Compute the effective design width of the

compression ﬂange of the beam shown in Fig. 3.22 using

the U.S. customary unit.

(a) For strength determination—assume that the compres-

sive stress in the ﬂange without considering the safety

factor is 25 ksi.

(b) For serviceability determination—assume that the com-

pressive stress in the ﬂange under the service or allow-

able load is 15 ksi.

Figure 3.22 Example 3.2.

SOLUTION

1. Strength Determination. As the ﬁrst step, compute λ

using Eq. (3.44) with the following values:

k = 4.0

w = 15.00 − 2(R + t)

= 15.00 − 2(0.1875 + 0.105) = 14.415 in.

14.415

0.105

= 137.286

f = 25 ksi

E = 29,500 ksi

λ =

1.052

√

(137.286)



29,500

= 2.102

Since λ>0.673, compute the reduction factor ρ

according to Eq. (3.43):

ρ =

1 − 0.22/2.102

2.102

= 0.426

Therefore, the effective design width for strength

determination is

b = ρw = (0.426)(14.415) = 6.14 in.

2. Serviceability Determination. By using Eq. (3.47) and

= 15 ksi,

λ =

1.052

√

(137.286)



29,500

= 1.628

Since λ>0.673,

ρ =

1 − 0.22/1.628

1.628

= 0.531

Therefore, the effective design width for serviceability

determination is

= ρw = (0.531)(14.415) = 7.654 in.

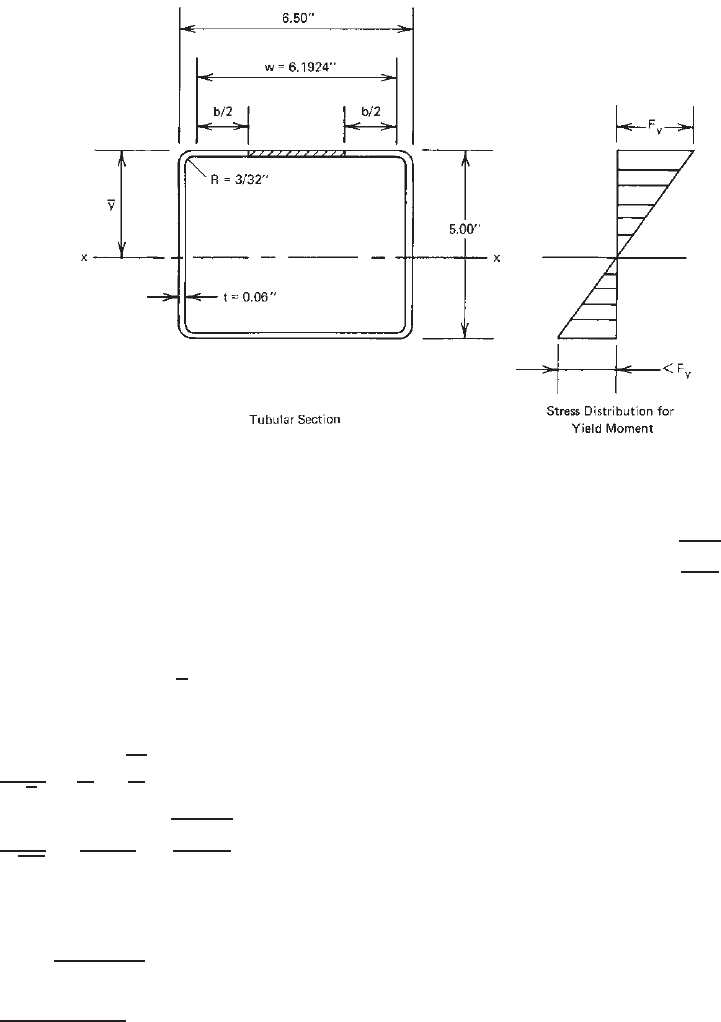
Example 3.3 Calculate the effective width of the

compression ﬂange of the box section (Fig. 3.23) to be

used as a beam bending about the x axis. Use F

= 33 ksi.

Assume that the beam webs are fully effective a nd that the

bending moment is based on initiation of yielding. Use the

U.S. customary unit.

68 3 STRENGTH OF THIN ELEMENTS AND DESIGN CRITERIA

Figure 3.23 Example 3.3.

SOLUTION. Because the compression ﬂange of the given

section is a uniformly compressed stiffened element, which

is supported by a web on each longitudinal edge, the

effective width of the ﬂange for strength determination can

be computed by using Eqs. (3.41)–(3.44) with k = 4.0.

Assume that the bending strength of the section is based

on initiation of yielding (procedure I of Section C3.1.1 of

the North American Speciﬁcation),

y ≥ 2.50 in. Therefore,

the slenderness factor λ for f = F

can be computed from

Eq. (3.44), that is,

λ =



1.052

√











1.052

√

4.0



6.1924

0.06





29,500

= 1.816

Since λ>0.673, use Eqs. (3.42) and (3.43) to compute the

effective width b as follows:

b = ρw =



1 − 0.22/λ





1 − 0.22/1.816

1.816



(6.1924) = 3.00 in.

The above discussion on the structural design of stiffened

compression elements is based on the North American

Speciﬁcation.

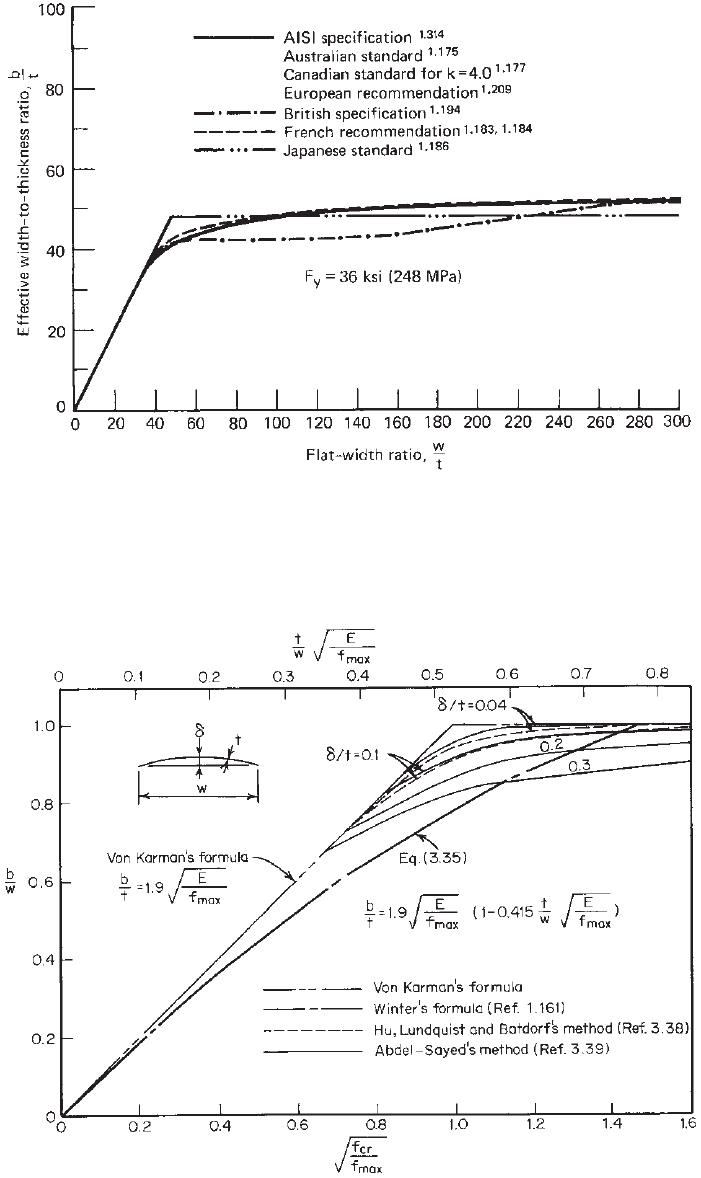
1.345

In other countries the design equations

and methods for determining the effective design width

may be different as compared with the AISI formulas.

For example, in the Japanese Standard

1.186

the effective

design width is independent of the ﬂat-width ratio w/t.

This approach is similar to Eq. (3.52), which was derived

by Lind et al.

3.20,3.21

on the basis of their statistical analysis

of the available experimental results:

b = 1.64t



max

(3.52)

Equation (3.52) was used in the Canadian Standard

during the period from 1974 through 1984.

In the British Standard the effective design width is

determined by using the w/t ratio and the design equations

given in Ref. 1.194. For the design of steel decks and

panels, European recommendations

1.209, 1.328

have adopted

Winter’s formula as given in Eqs. (3.38)–(3.40). In Refs.

1.183, 1.184, and 3.22 the French recommendations give

an effective design width similar to that permitted by the

North American Speciﬁcation.

The effective design widths of the stiffened compres-

sion element as determined by several design speciﬁca-

tions have been compared in Fig. 3.24. Reference 1.147

included comparisons of different speciﬁcations being used

in Australia, China, Eastern Europe, Japan, North America,

and Western Europe. Additional information on effective

design width can be found in Refs. 3.23–3.37.

Inﬂuence of Initial Imperfection on Effective Design

Width. The load-carrying capacity of stiffened compres-

sion elements is affected by the initial imperfection of the

plate. The larger the initial imperfection, the smaller the

capacity.

The inﬂuence of initial imperfection on the effective

design width has previously been studied by Hu et al.

3.38

and by Abdel-Sayed.

3.39

Figure 3.25 shows the theoretical

ratio of effective width to actual width, b/w, affected

by various values of initial imperfections. Imperfect

STRUCTURAL BEHAVIOR OF COMPRESSION ELEMENTS AND DESIGN CRITERIA 69

Figure 3.24 Comparison of effective design widths for load determination by using various design

speciﬁcations.

Figure 3.25 Effect of initial imperfection on effective design width.

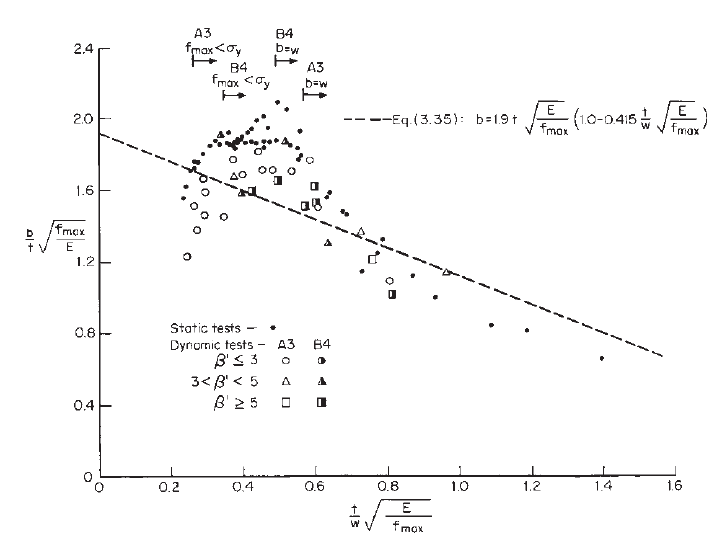
70 3 STRENGTH OF THIN ELEMENTS AND DESIGN CRITERIA

plates have also been studied extensively by Dawson and

Walker,

3.40

Sherbourne and Korol,

3.41

Hancock,

3.42

and

Maquoi and Rondal.

3.43

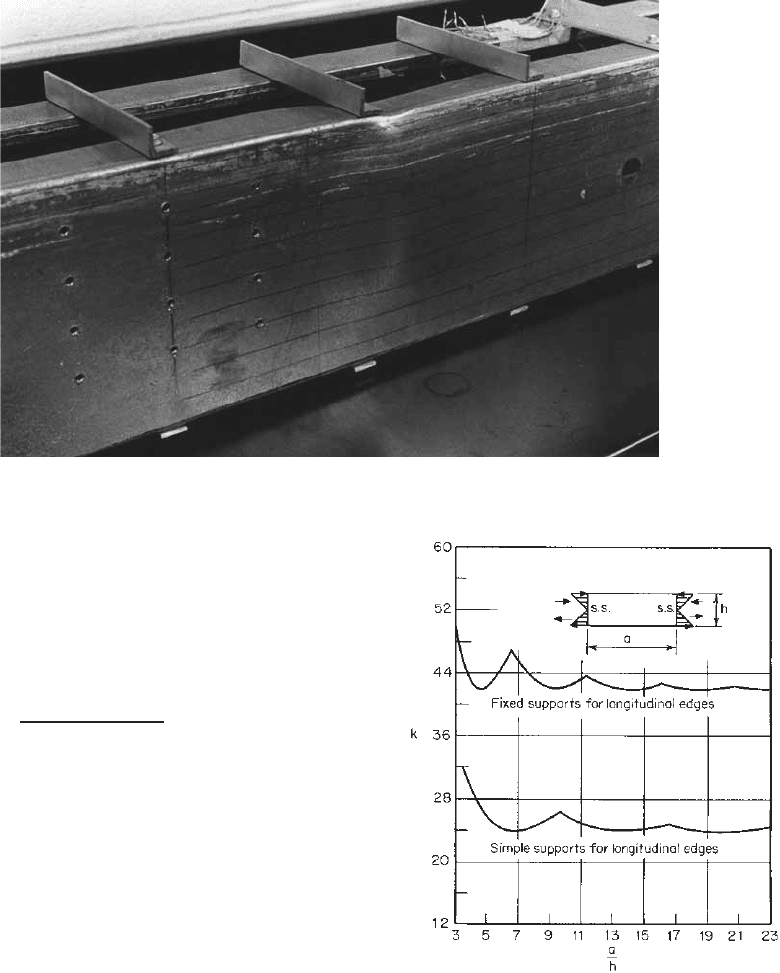
Inﬂuence of Impact Loading on Effective Design Width.

Previous discussion on effective width was concerned with

the compression elements subjected to static loading. This

type of loading condition is primarily applicable to the

design of cold-formed steel members used in building

construction.

As indicated in Section 1.1, cold-formed steel members

are also used in car bodies, railway coaches, various types

of equipment, storage racks, highway products, and bridge

construction, all of which are subjected to dynamic loads.

Since members subjected to dynamic loads behave differ-

ently than those subjected to static loads, the question arises

as to whether direct application of the AISI design criteria

based on static loading is appropriate. In order to develop

the necessary information on this topic, research work has

been conducted by Culver and his collaborators at Carnegie-

Mellon University to study analytically and experimen-

tally the behavior of thin compression elements, beams,

and columns subjected to dynamic or time-dependent

3.44–3.49

It was found that the effective design width

formula [Eq. (3.35)] satisﬁes both the static and the dynamic

results to the same degree of accuracy.

3.44,3.46

Figure 3.26

shows the correlation between the test data and Eq. (3.35).

In this ﬁgure β



is the ratio of the time duration of the

stress pulse to the fundamental period of the compression

ﬂange treated as a simply supported plate. This subject has

also been studied at the University of Missouri-Rolla under

a project on automotive structural components.

3.50,2.67–2.71

In Ref. 2.103, Rhodes and Macdonald reported channel

section beams under static and impact loading.

3.5.1.2 Beam Webs and Stiffened Elements with Stress

Gradient When a ﬂexural member is subjected to

bending moment, the compression portion of the web may

buckle due to the compressive stress caused by bending.

Figure 3.27 shows a typical pattern of bending failure of

beam webs.

Prior to 1986, the design of beam webs in the United

States was based on the full web depth and the allowable

bending stress speciﬁed in the 1980 and earlier editions of

the AISI Speciﬁcation. In order to unify the design methods

for webs and compression ﬂanges, the “effective web depth

approach” was adopted in the 1986 edition of the AISI

Speciﬁcation.

1.4

The same design approach was used in the

1996 AISI Speciﬁcation

1.314

and is retained in the North

American Speciﬁcation.

1.336,1.345

Figure 3.26 Correlation between effective design width formula and test data.

3.46

STRUCTURAL BEHAVIOR OF COMPRESSION ELEMENTS AND DESIGN CRITERIA 71

Figure 3.27 Typical bending failure pattern for channel sections.

3.60

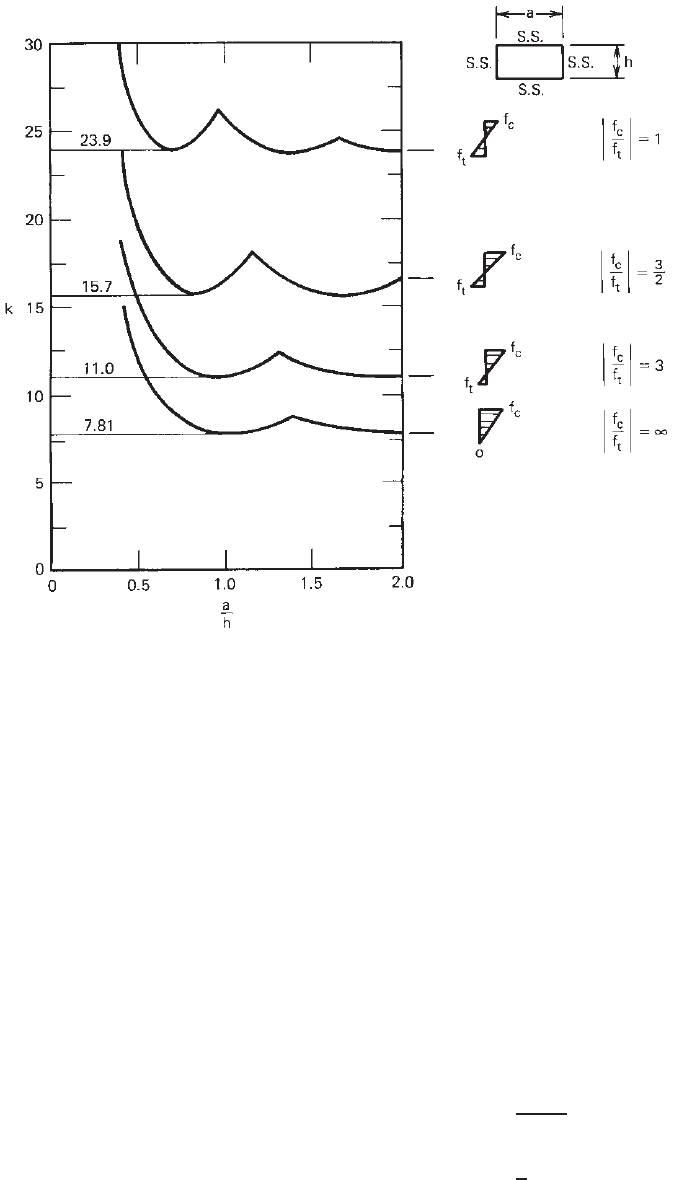
Web Buckling due to Bending Stress. The buckling

of disjointed ﬂat rectangular plates under bending with

or without longitudinal loads has been investigated by

Timoshenko, Schuette, McCulloch, Johnson, and Noel.

3.1,3.2

The theoretical critical buckling stress for a ﬂat rectangular

plate under pure bending can be determined by Eq. (3.53):

kπ

12(1 − μ

)(h/t)

(3.53)

where h is the depth of the web and k is the buckling coef-

ﬁcient. For long plates the value of k was found to be 23.9

for simple supports and 41.8 for ﬁxed supports as listed in

Table 3.4. The relationships between the buckling coefﬁ-

cient and the aspect ratio a/h are shown in Fig. 3.28. When

a s imply supported plate is subjected to a compressive

bending stress higher than the tensile bending stress, the

buckling coefﬁcient k is reduced according to the bending

stress ratio f

asshowninFig.3.29.

3.7

In practice the bending strength of a beam web not only

is affected by the web slenderness ratio h/t, the aspect ratio

a/h, and the bending stress ratio f

but also depends

on the mechanical properties of material (E , F

,andμ)

and the interaction between ﬂange and web components. In

addition, the buckling coefﬁcient k for the web is inﬂuenced

by the actual edge restraint provided by the beam ﬂange.

Because the derivation of an exact analytical solution for the

stability and the postbuckling strength of plate assemblies is

extremely cumbersome, the AISI design criteria have been

based on the results of tests.

Figure 3.28 Bending buckling coefﬁcients of plates vs. aspect

ratio, a/h.

3.1

Postbuckling Strength and Effective Depth of Webs.

In the past, several design formulas for computing the

effective web depth have been developed by Bergfelt,

Thomasson, Kallsner, Hoglund, DeWolf, Gladding,

LaBoube, and Yu

3.51−3.61

to account for the actual buck-

ling strength and the postbuckling behavior of beam

webs. The effective web depth approach has been used in

several speciﬁcations.

3.62,3.63

In 1986, Cohen and Pekoz

3.64

72 3 STRENGTH OF THIN ELEMENTS AND DESIGN CRITERIA

Figure 3.29 Buckling coefﬁcient k for simply supported plates subjected to nonuniform longitu-

dinal bending stress.

3.7

(Reproduced with permission from Chatto & Windus, London.)

evaluated the test results reported by LaBoube and

Yu,

3.59–3.61

Cohen and Pekoz,

3.64

Kallsner,

3.54

Johnson,

3.65

He,

3.66

and van Neste

3.67

and developed the needed design

formulas for webs connected to stiffened, unstiffened, and

partially stiffened compression ﬂanges. Some statistical

data on the correlation are given in Ref. 3.17.

Consequently, design equations were included in

Section B2.3 of the 1986 edition of the AISI Speciﬁcation

for computing the effective width of webs and stiffened

elements with a stress gradient as shown in Fig. 3.30. The

same equations were used in the 1996 edition of the AISI

Speciﬁcation.

Because the AISI design equations for computing the

effective width of webs implicitly assumed that the beam

ﬂange provided beneﬁcial restraint to the web, the test

data on ﬂexural tests of C - and Z-sections summarized by

Schafer and Pekoz

3.168

indicated that the AISI equations

can be unconservative if the overall web depth (h

)to

overall ﬂange width (b

) ratio exceeds 4. In 2001, due

to the lack of a comprehensive method for handling web

and ﬂange interaction, the North American Speciﬁcation

adopted the following two-part approach in Section B.2.3

for computing the effective width of beam webs and

other stiffened elements under a stress gradient. The same

design equations are retained in the 2007 edition of the

Speciﬁcation:

(a) Strength Determination

(i) For webs under a stress gradient (f

in compression

and f

in tension as shown in Fig. 3.30a):

k = 4 + 2(1 + ψ)

+ 2(1 + ψ) (3.54)

For h

≤ 4

3 + ψ

(3.55a)

when ψ>0.236 (3.55b)

= b

− b

when ψ ≤ 0.236 (3.55c)

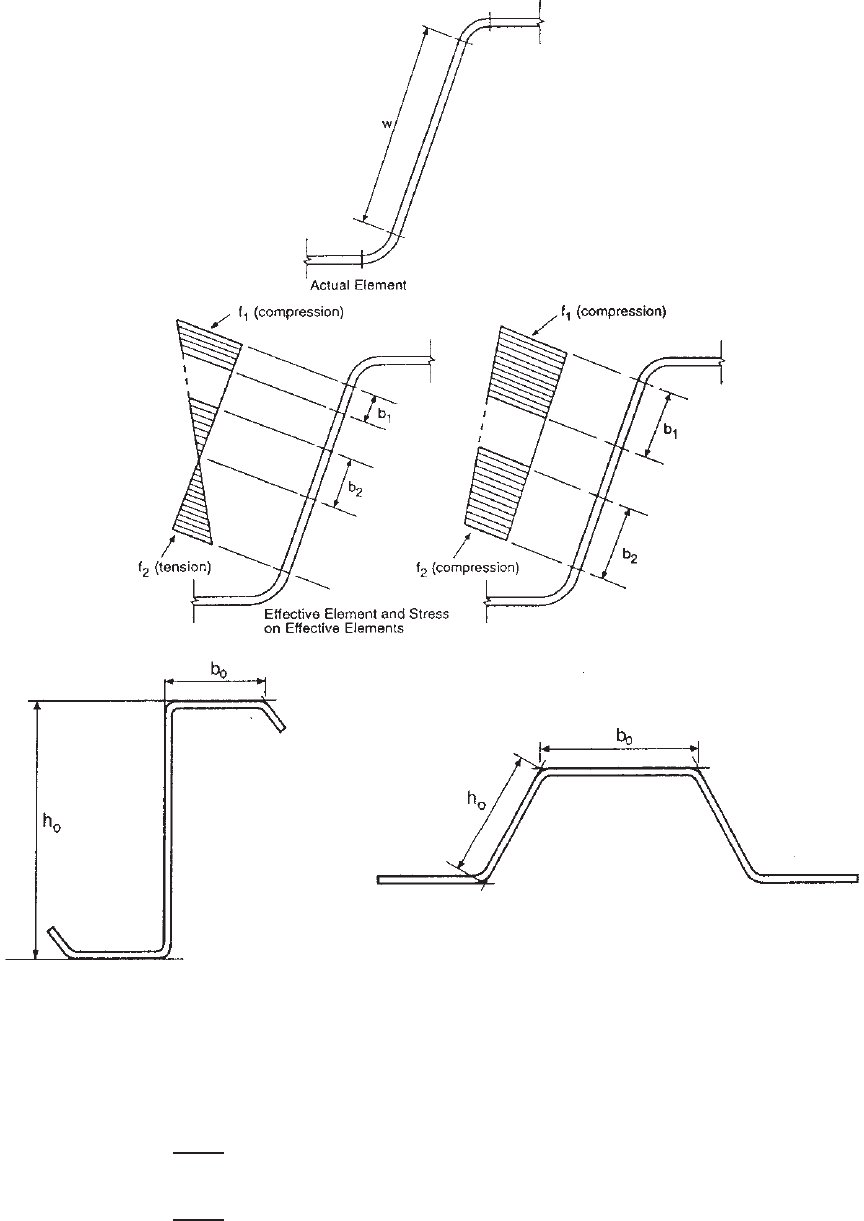
STRUCTURAL BEHAVIOR OF COMPRESSION ELEMENTS AND DESIGN CRITERIA 73

(a) (b)

(c)

Figure 3.30 (a, b) Stiffened elements with stress gradient and webs.

1.345

sions of webs and stiffened elements under stress gradient.

1.345

For h

> 4

3 + ψ

(3.56a)

1 + ψ

− b

(3.56b)

In addition, b

+ b

shall not exceed the compression

portion of the web calculated on the basis of the

effective section.

(ii) For other stiffened elements under a stress gradient

and f

in compression as shown in Fig. 3.30b)

k = 4 + 2(1 − ψ)

+ 2(1 − ψ) (3.57)

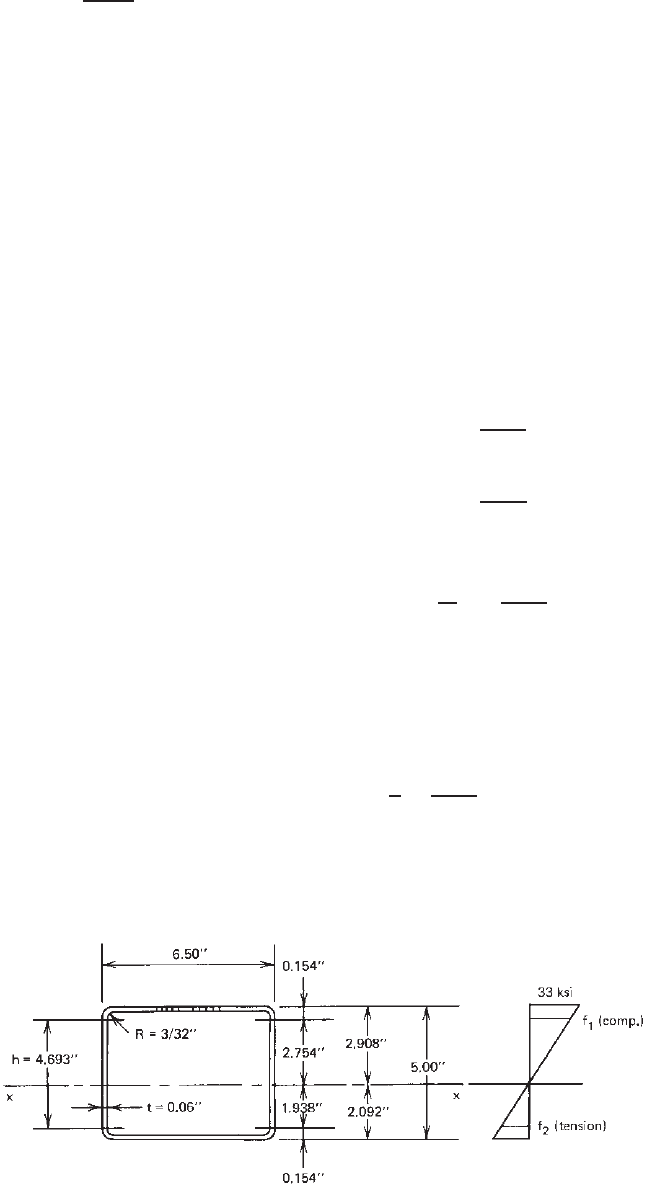
74 3 STRENGTH OF THIN ELEMENTS AND DESIGN CRITERIA

3 − ψ

(3.58a)

= b

− b

(3.58b)

In the above expressions,

= effective width as shown in Fig. 3.30

= effective width b determined in accordance

with Eq. (3.41) through Eq. (3.44) with

substituted for f and k determined from

Eq. (3.54) or (3.57)

= out-to-out width of compression ﬂange as

showninFig.3.30c

= stresses shown in Fig. 3.30 calculated on

basis of effective section, where f

and f

are both compression, f

≥ f

= out-to-out depth of web as shown in

Fig. 3.30c

k = plate buckling coefﬁcient

ψ =|f

| (absolute value)

(b) Serviceability Determination. The effective widths used

in determining serviceability shall be calculated in

accordance with Eqs. (3.54)–(3.58) except that f

and

are substituted for f

and f

,wheref

and f

are the computed stresses f

and f

based on the

effective section at the load for which serviceability is

determined.

In the foregoing design provisions, Eqs. (3.55a), (3.55b),

and (3.55c)forh

≤ 4 were adopted from the 1996

edition of the AISI Speciﬁcation, except that the stress ratio

ψ is deﬁned as an absolute value. Equations (3.56a)and

(3.56b), originally developed by Cohen and Pekoz,

3.64

were

selected for h

> 4. As compared with the 1996 AISI

Speciﬁcation, the change of Eq. (3.56b)forb

would result

in somewhat lower strengths when h

> 4 b

. It should be

noted that due to the use of an absolute value for ψ,some

signs were changed in the design equations of the North

American Speciﬁcation.

Example 3.4 For the box section used in Example 3.3,

it can be shown that the distance from the top compres-

sion ﬁber to the neutral axis is 2.908 in. if the beam

webs are fully effective. Check these two beam webs and

determine whether they are fully effective according to

Eqs. (3.54)–(3.56) for strength determination. Use F

33 ksi and the U.S. customary unit.

SOLUTION. From Fig. 3.31, stresses f

and f

are

computed as follows:

= 33



2.754

2.908



= 31.25 ksi (compression)

= 33



1.938

2.908



= 22.00 ksi (tension)

According to Eqs. (3.54) for webs under a stress gradient,

ψ =



22.00

31.25



= 0.704

k = 4 + 2(1 + ψ)

+ 2(1 + ψ)

= 4 +2(1 + 0.704)

+ 2(1 + 0.704) = 17.304

h = 4.693 in.

4.693

0.06

= 78.21 < 200 OK

(see Section 3.2 for the maximum h/t ratio). The effec-

tive depth b

of the web can be computed in accordance

Figure 3.31 Example 3.4.