Yu W., LaBoube R.A. Cold-Formed Steel Design

Подождите немного. Документ загружается.

ADDITIONAL INFORMATION 95

for a multiple-hole pattern that ﬁts within a noncircular

virtual hole, while Fig. 3.65 illustrates the dimension d

for a rectangular hole that exceeds the limits of 2.5 in.

(64 mm) × 4.5 in. (114 mm) but still ﬁts within an allowable

circular virtual hole. For each case, the provisions apply to

the geometry of the virtual hole, not the actual hole or

holes.

1.333

For the effect of web holes on the shear strength and

web crippling strength of C-sections, see Section 4.3 on

the design of beam webs.

3.7 PLATE BUCKLING OF STRUCTURAL

SHAPES

Section 3.5 discussed the local buckling of s tiffened and

unstiffened compression elements, for which the edges were

assumed to be simply supported. If the actual restraining

effects of adjoining cross-sectional elements are taken into

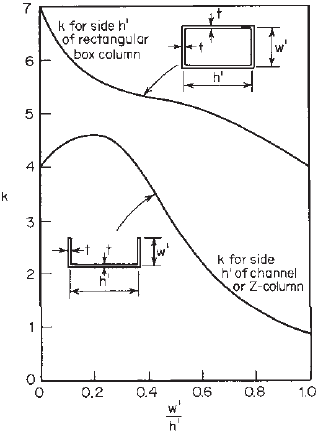
account, the plate buckling coefﬁcient k for box sections,

channels, and Z-sections used as columns can be found

from Fig. 3.66. These curves are based on the charts

developed by Kroll, Fisher, and Hei-merl.

3.116

Additional

information can be found from Refs. 1.94, 1.158, 3.8,

3.80, 3.117–3.123, 3.195, and 3.196 and in Chapter 5 on

compression members.

The advantages of using a numerical solution for the

design of cold-formed steel members a re discussed by

Schafer and Pekoz in Refs. 3.195 and 3.196. The element

interaction can be handled properly by the numerical

solution.

Since 2001, the AISI North American speciﬁcation

permits the use of rational analysis for determining the

design strength and stiffness of cold-formed steel members

in Section A1.2. Consequently, Appendix 1, Design of

Cold-Formed Steel Structural Members Using the Direct

Strength Method, was developed in 2004 and added in

Figure 3.66 Plate buckling coefﬁcient k for side h



of columns.

the 2007 edition of the North American Speciﬁcation. For

details, see Chapter 15.

3.8 ADDITIONAL INFORMAT ION

The strength of thin compression elements and the current

design criteria were discussed in this chapter on the basis of

the publications referred to in the text. Additional informa-

tion on the strength of compression elements and members

can also be found from the publications included in the list

of references for this chapter.

The structural behavior of webs of beams subjected to

shear or bearing is discussed in Chapter 4 on the design

of ﬂexural members. The buckling behavior of closed

cylindrical tubular members is discussed in Chapter 7.

CHAPTER 4

Flexural Members

4.1 GENERAL REMARKS

Beams are used to support transverse loads and/or applied

moment. Cold-formed steel sections such as I-sections,

C-sections (channels), Z-shapes, angles, T-sections, hat

sections, and tubular members (Fig. 1.2) and decks and

panels (Fig. 1.11) can be used as ﬂexural members.

In the design of cold-formed steel ﬂexural members,

consideration should ﬁrst be given to the moment-resisting

capacity and the stiffness of the member. It may be found

that in many cases the moment of inertia of the section

is not a constant value but varies along the span length

due to the noncompactness of the thin-walled section and

the variation of the moment diagram. The design method

is discussed in this chapter. Second, the webs of beams

should be checked for shear, combined bending and shear,

web crippling, and combined bending and web crippling.

In addition to the design features discussed above, the

moment-resisting capacity of the member may be limited by

lateral-torsional buckling of the beam, particularly when the

open section is fabricated from thin material and laterally

supported at relatively large intervals. For this reason,

ﬂexural members must be braced adequately in accordance

with the bracing requirements prescribed in the North

American Speciﬁcation; otherwise a low design moment

has to be used. For some open sections with edge-stiffened

compression ﬂanges, distortional buckling may be critical.

Unlike hot-rolled heavy s teel sections, in the design

of thin-walled cold-formed steel beams, special problems

such as shear lag and ﬂange curling are also considered

to be important matters due to the use of thin material.

Furthermore, the design of ﬂexural members can be even

more involved if the increase of steel mechanical properties

due to cold work is to be utilized.

Based on the above general discussion, the following

design features are considered in this chapter with some

design examples for the purpose of illustration:

1. Bending strength and deﬂection

2. Design of webs for shear, combined bending and

shear, web crippling, and combined bending and web

crippling

3. Bracing requirements

4. Shear lag

5. Flange curling

In general, long-span, shallow beams are governed by

deﬂection and medium-length beams are controlled by

bending strength. For short-span beams, shear strength may

be critical.

For design tables and charts, reference should be made

to Part II of the AISI Design Manual.

1.349

4.2 BENDING STRENGTH AND DEFLECTION

4.2.1 Introduction

In the design of ﬂexural members, sufﬁcient bending

strength must be provided, and at the same time the deﬂec-

tion of the member under s ervice loads should not exceed

speciﬁc limitations.

A. ASD Method

According to the design format discussed in Section

3.3.1.1 for the A SD method, Eq. (4.1) gives the

following structural safety requirement for the ﬂexural

or bending strength:

M ≤ M

(4.1)

where M is the required ﬂexural strength or bending

moment for ASD computed from the load combinations

discussed in Section 3.3.1.2 and M

is the allowable

ﬂexural strength or bending moment determined by Eq.

(4.2):



(4.2)

where 

= 1.67 is the safety factor for ﬂexural or

bending strength on the basis of Section C 3.1 of the

North American Speciﬁcation and M

is the smallest

nominal ﬂexural strength or moment determined from

the following ﬁve design considerations:

1. Section strength or bending moment of the cross

section calculated in accordance with Section 4.2.2

2. Lateral-torsional buckling strength calculated in

accordance with Section 4.2.3

98 4 FLEXURAL MEMBERS

3. Distortional buckling strength calculated in accor-

dance with Section 4.2.4 for I-, Z-, C - and other

open cross-sectional beams having edge-stiffened

compressions ﬂanges

4. Section strength of beams having one ﬂange through

fastened to deck or sheathing determined in accor-

dance with Section 4.2.5

5. Section strength of beams having one ﬂange fastened

to a standing seam roof system determined in accor-

dance with Section 4.2.6

In addition to the above-listed ﬁve cases, consid-

eration should also be given to shear lag problems

for unusually short span beams (see Section 4.2.7).

The current North American design provisions consider

torsional effects in Section C3.6 of the Speciﬁcation

for the loads that do not pass through the shear center

of the cross section.

1.345

For torsional analysis, see

Appendix B.

B. LRFD Method

Based on the design format discussed in Section

3.3.2.1 for the LRFD method, the structural safety

requirement for the ﬂexural or bending strength is

expressed in Eq. (4.3):

≤ φ

(4.3)

where M

is the required ﬂexural strength or bending

moment for LRFD computed from load combinations

(see Section 3.3.2.2);

, the resistance factor for reducing the ﬂex-

ural strength or bending moment, equals 0.95 for the

nominal section strength of ﬂexural members with stiff-

ened or partially stiffened compression ﬂanges (Section

4.2.2) and 0.90 for the nominal section strength of

ﬂexural members w ith unstiffened compression ﬂanges

(Section 4.2.2), the nominal lateral–torsional buckling

strength (Section 4.2.3), the nominal distortional

buckling strength (Section 4.2.4), the section strength

of beams having one ﬂange through fastened to deck

or sheathing (Section 4.2.5), and the section strength of

beams having one ﬂange fastened to a standing seam

roof system (Section 4.2.6); and φ

is the design

ﬂexural strength or bending moment, w here M

was

deﬁned above for the ASD method.

C. LSD Method

Based on the design format discussed in Section

3.3.3.1 for the LSD method, the structural safety

requirement for the ﬂexural or bending strength is

expressed as

≤ φ

where M

is the required ﬂexural resistance for LSD

computed from load combinations (see Section 3.3.3.2);

is the nominal ﬂexural resistance; and φ

equals 0.90

for the nominal section resistance (Section 4.2.2), the

nominal lateral–torsional buckling resistance (Section

4.2.3), and the nominal ﬂexural resistance of beams

having one ﬂange through fastened to deck or sheathing

(Section 4.2.5) and 0.85 for the nominal distortional

buckling resistance (Section 4.2.4), where φ

is the

factored ﬂexural resistance.

4.2.2 Section Strength or Bending Moment

of the Cross Section

Section C3.1.1 of the 2007 edition of the North American

speciﬁcation includes two design procedures for calculating

the section strength of ﬂexural members. Procedure I is

based on “initiation of yielding” and procedure II is based

on “inelastic reserve capacity.” Both design procedures are

discussed here.

4.2.2.1 Initiation of Yielding In procedure I of the AISI

speciﬁcation, the nominal moment M

of the cross section

is the effective yield moment M

determined on the basis

of the effective areas of ﬂanges and the beam web. The

effective width of the compression ﬂange and the effec-

tive depth of the web can be computed from the design

equations presented in Chapter 3.

Similar to the design of hot-rolled steel shapes, the yield

moment M

of a c old-formed steel beam is deﬁned as

the moment at which an outer ﬁber (tension, compression,

or both) ﬁrst attains the yield stress of steel. This is the

maximum bending capacity to be used in elastic design.

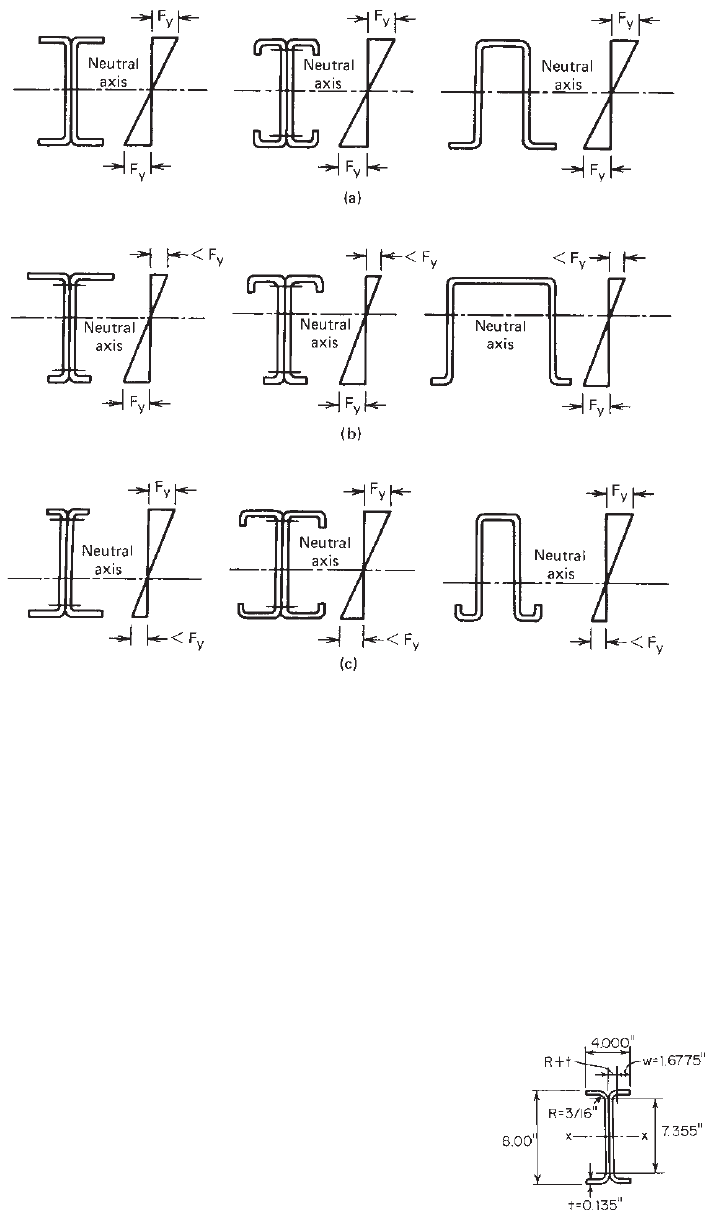
Figure 4.1 shows s everal types of stress distribution for

yield moment based on different locations of the neutral

axis. For balanced sections (Fig. 4.1a), the outer ﬁbers in

the compression and tension ﬂanges reach the yield stress at

the same time. However, if the neutral axis is eccentrically

located, as shown in Figs. 4.1b and c, the initial yielding

takes place in the tension ﬂange for case b and in the

compression ﬂange for case c.

Based on the above discussion, the nominal section

strength for initiation of yielding is calculated by using Eq.

(4.4):

= M

= S

(4.4)

where F

= design yield stress

= elastic section modulus of effective section

calculated with extreme c ompression or

tension ﬁber a t F

In cold-formed steel design, S

is usually computed by

using one of the following two cases:

1. If the neutral axis is closer to the tension than to

the compression ﬂange, as shown in Fig. 4.1c,the

BENDING STRENGTH AND DEFLECTION 99

Figure 4.1 Stress distribution for yield moment: (a) balanced sections; (b) neutral axis close

to compression ﬂange (initial yielding in tension ﬂange); (c) neutral axis close to tension ﬂange

(initial yielding in compression ﬂange).

maximum stress occurs in the compression ﬂange, and

therefore the plate slenderness factor λ and the effec-

tive width of the compression ﬂange are determined

by the w /t ratio and f = F

in Eq. (3.44). Of course,

this procedure is also applicable to those beams for

which the neutral axis is located at the middepth of

the section, as shown in Fig. 4.1a.

2. If the neutral axis is closer to the compression than

to the tension ﬂange, as shown in Fig. 4.1b,the

maximum stress of F

occurs in the tension ﬂange.

The stress in the compression ﬂange depends on the

location of the neutral axis, which is determined by

the effective area of the section. The latter cannot be

determined unless the compressive stress is known.

The closed-form solution of this type of design is

possible but would be a very tedious and complex

procedure. It is therefore customary to determine

the sectional properties of the section by successive

approximation.

The calculation of the nominal moment on the basis of

initiation of yielding and the determination of the design

moment are illustrated in Examples 4.1–4.4.

Example 4.1 Use the ASD and LRFD methods to check

the adequacy of the I-section with an unstiffened compres-

sion ﬂange as shown in Fig. 4.2. The nominal moment for

section strength is computed on the basis of initiation of

Figure 4.2 Example 4.1.

100 4 FLEXURAL MEMBERS

yielding by using F

= 50 ksi. Assume that lateral bracing

is adequately provided. The dead-load moment M

30 in.-kips and the live-load moment M

= 150 in.-kips.

SOLUTION

A. ASD Method

1. Calculation of Sectional Properties. The sectional

properties of the corner element can be obtained from

Table 4.1. For R =

in. and t = 0.135 in.,

= I

=0.0003889 in.

A = 0.05407 in.

x = y = 0.1564 in.

For the unstiffened ﬂange,

w =

4.000

− (R + t) = 1.6775 in.

1.6775

0.135

= 12.426 < 60

OK according to Section 3.2

Since the compression ﬂange is an unstiffened

element and the neutral axis is either at middepth or

closer to the tension ﬂange, use Eqs. (3.41)–(3.44)

with k = 0.43 and f = F

= 50 ksi. Therefore

λ =

1.052

√







1.052

√

0.43

(12.426)



29,500

= 0.821 > 0.673 [Eq. (3.44)]

ρ =

1 − 0.22/λ

1 − 0.22/0.821

0.821

= 0.892 [Eq. (3.43)]

b = ρw = 0.892(1.6775)

= 1.4963 in.

By using the effective width of the compression

ﬂange and a ssuming the web is fully effective, the

location of the neutral axis, the moment of inertia

and the elastic section modulus of the effec-

tive section S

can be computed as shown in table

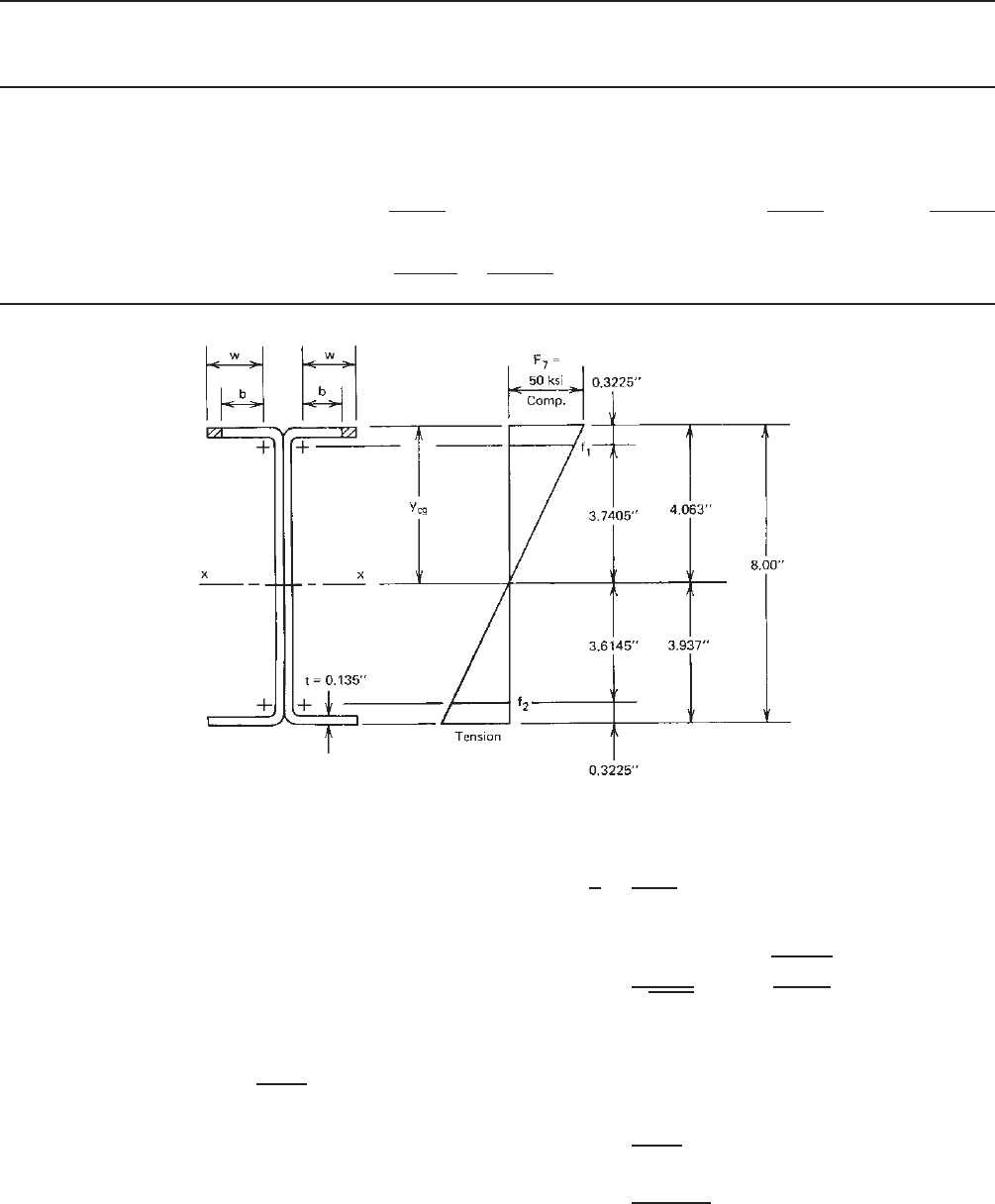
on the following page.

Since y

>d/2 = 4.00 in., initial yield occurs

in the compression ﬂange. Prior to computing the

moment of inertia, check the web for full effec-

tiveness by using Fig. 4.3 and Section 3.5.1.2 as

follows:

= 50



3.7405

4.063



= 46.03 ksi (compression)

= 50



3.6145

4.063



= 44.48 ksi (tension)

ψ =



= 0.966

k = 4 + 2(1 + ψ)

+ 2(1 + ψ)

= 4 +2(1 + 0.966)

+ 2(1 + 0.966) = 23.13

[Eq. (3.54)]

Table4.1 One90

◦

Corner, Dimensions and Properties

Dimensions Properties

Centroid

Inside Moment of Coordinates Blank

Thickness t (in.) Radius R (in.) Inertia I

= I

(in.

) x = y (in.) Area A (in.

) Width (in.)

0.135 0.1875 0.0003889 0.1564 0.05407 0.3652

0.105 0.1875 0.0002408 0.1373 0.03958 0.3495

0.075 0.0938 0.0000301 0.0829 0.01546 0.1865

0.060 0.0938 0.0000193 0.0734 0.01166 0.1787

0.048 0.0938 0.0000128 0.0658 0.00888 0.1724

0.036 0.0625 0.00000313 0.0464 0.00452 0.1170

Notes: (1) Stock width of blank taken at t/3 distance from inner surface.

(2) 1 in. = 25.4 mm.

BENDING STRENGTH AND DEFLECTION 101

Distance from

Top Fiber yAy Ay

Element Area A (in.

)(in.)(in.

)(in.

)

Top ﬂange 2(1.4963)(0.135) = 0.4040 0.0675 0.0273 0.0018

Top corners 2(0.05407) = 0.1081 0.1564 0.0169 0.0026

Webs 2(7.355)(0.135) = 1.9859 4.0000 7.9436 31.7744

Bottom corners 2(0.05407) = 0.1081 7.8436 0.8479 6.6506

Bottom ﬂange 2(1.6775)(0.135) =

0.4529 7.9325 3.5926 28.4983

Total 3.0590 12.4283 66.9277



(Ay)



12.4283

3.0590

= 4.063 in.

Figure 4.3 Stress distribution in webs.

From Fig. 4.2,

= out-to-out depth of web

= 8.00 in.

= out-to-out width of the compression

ﬂange of each channel = 2.00 in.

Since h

= 4, then use Eq. (3.55a),

3 + ψ

where b

is the effective width of the web deter-

mined in accordance with Eqs. (3.41)–(3.44) with f

substitued for f and k = 23.13 as follows:

h = 7.355 in.

7.355

0.135

= 54.48 < 200

OK according to Section 3.2

λ =

1.052

√

23.13

(54.48)



46.03

29,500

= 0.471 < 0.673

[Eq. (3.44)]

ρ = 1.0 [Eq. (3.43)]

= h = 7.355 in.

3 + ψ

7.355

3 + 0.966

= 1.855 in. [Eq. (3.55a)]

102 4 FLEXURAL MEMBERS

Since ψ>0.236,

= 3.6775 in. [Eq. (3.55b)]

+ b

= 1.855 + 3.6775 = 5.5325 in.

Since b

+ b

is greater than the compression portion

of the web of 3.7405 in., the web is fully effective a s

assumed. The total I

is determined as



(Ay

) = 66.9277

web

= 2(

)(0.135)(7.355)

= 8.9522

−







)

= (3.0590)(4.063)

=−50.4979

= 25.3820 in.

The elastic section modulus relative to the top

ﬁber is

25.3820

4.063

= 6.247 in.

2. Nominal and Allowable Moments. The nominal

moment for section strength is

= S

= (6.247)(50) = 312.35 in.-kips

Theallowablemomentis



312.35

1.67

= 187.0in.-kips

3. Required Moment. Based on the ASD load combina-

tion discussed in Section 3.3.1.2, the required moment

for the given dead-load moment and live-load moment

is computed as follows:

M = M

+ M

= 30 + 150 = 180 in.-kips

Since M <M

, the I-section is adequate for the ASD

method.

B. LRFD Method

1. Nominal and Design Moments. The nominal moment

for the LRFD method is the same as that used for the

ASD method, that is,

= 312.35 in.-kips

The design moment for the I-section having an unstiff-

ened compression ﬂange (φ

= 0.90) is

= 0.90(312.35) = 281.12 in.-kips

2. Required Moment. According to the load factors and

the load combinations discussed in Section 3.3.2.2,

the required moment for the given dead-load moment

and live-load moment can be computed as follows:

= 1.4D

= 1.4(30) = 42.00 in.-kips

= 1.2D + 1.6L

= 1.2(30) + 1.6(150)

= 276.00 in.-kips ⇐ controls

Since M

<φ

, the I-section is also adequate for

the LRFD method.

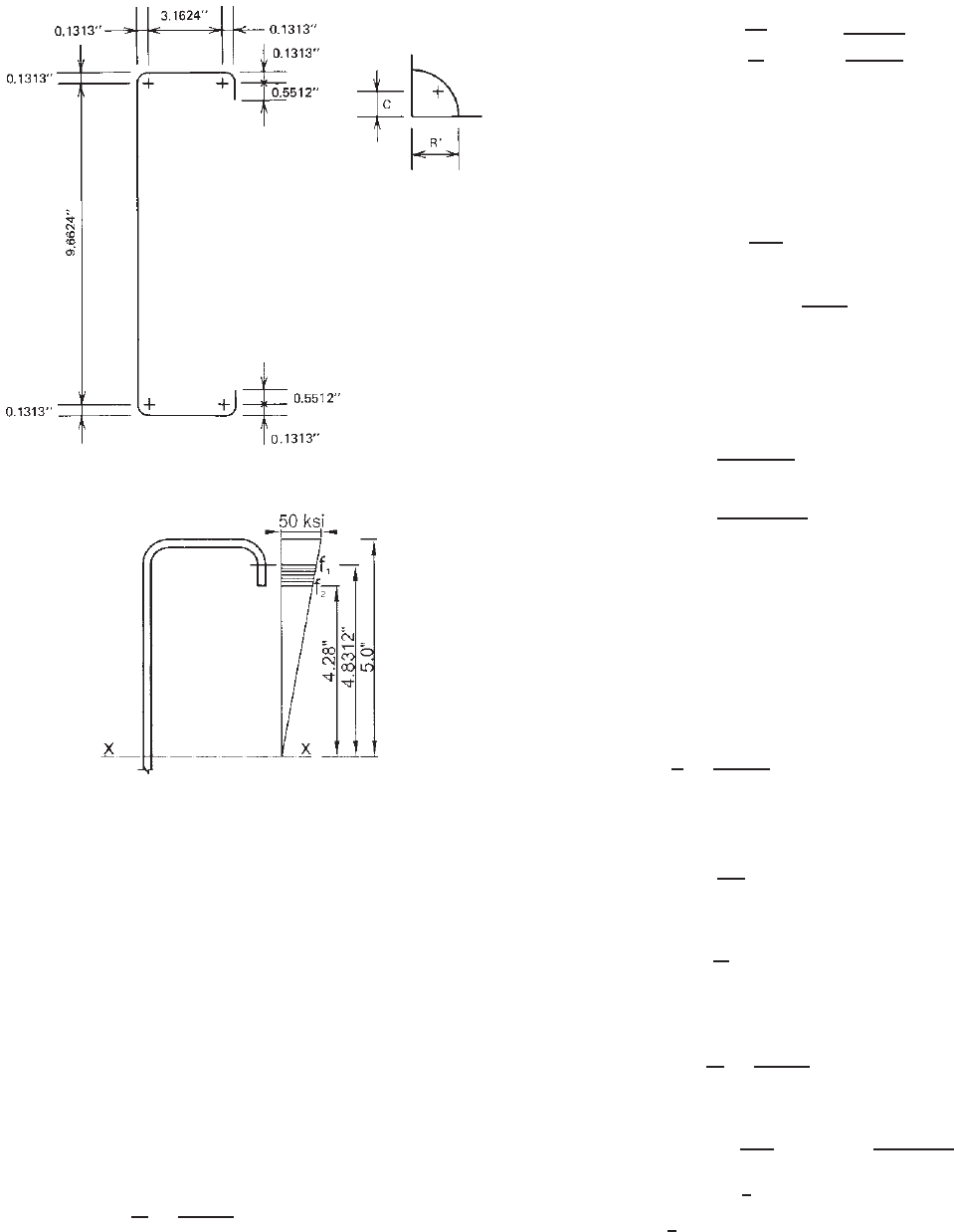
Example 4.2 For the C-section with an edge stiffener as

shown in Fig. 4.4, determine the allowable moment (M

)

about the x axis for the ASD method and the design moment

(φ

) for the LRFD method. Assume that the yield stress

of steel is 50 ksi and that lateral bracing is adequately

provided. Use the linear method. The nominal moment is

determined by initiation of yielding.

SOLUTION

A. ASD Method

1. Calculation of Sectional Properties. In order to

simplify the calculation, line elements, as shown in

Fig. 4.5a, are used for the linear method.

i. Corner Element (Figs. 1.32 and 4.5a)



= R +

t = 0.131 in.

Figure 4.4 Example 4.2 (same as Fig 3.50).

BENDING STRENGTH AND DEFLECTION 103

(a)

(

)

Figure 4.5 (a) Line elements. ( b) Compression stresses f

and f

Arc length:

L = 1.57R



= 0.206 in.

c = 0.637R



= 0.0836 in.

ii. Effective Width of the Compression Flange. For the

given C-section with equal ﬂanges, the neutral axis

is located either at the middepth or closer to the

tension ﬂange. Therefore, use f = F

= 50 ksi to

compute the effective width of the compression

ﬂange according to Section 3.5.3.1a. For the

compression ﬂange,

w = 3.50 − 2(R + t) = 3.1624 in.

3.1624

0.075

= 42.17

From Eq. (3.80)

S = 1.28



= 1.28



29,500

= 31.09

0.328S = 10.20

Since w/t > 0.328 S , use Eq. (3.81) to compute

the required moment of inertia of the edge stiffener

as follows:

= 399t



w/t

− 0.328



= 399(0.075)



42.17

31.09

− 0.328



= 13.73 × 10

−3

in.

The above computed value should not exceed the

following value:



115(w/t)

+ 5





115(42.17)

31.09

+ 5



(0.075)

= 5.093 × 10

−3

in.

Therefore, use I

= 5.093 × 10

−3

in.

For the

simple lip edge stiffener used for the given channel

section,

D = 0.720 in.

d = D − (R + t) = 0.5512 in.

0.5512

0.075

= 7.35

By using Eq. (3.83), the moment of inertia of the

full edge stiffener is

= 1.047 × 10

−3

in.

From Eq. (3.82),

= 0.206 < 1.0OK

The effective width b of the compression ﬂange

can be calculated as follows:

0.72

3.1624

= 0.228

From Eq. (3.84),

n = 0.582 −

w/t

= 0.582 −

42.17

4 × 31.09

= 0.243 <

Use n =

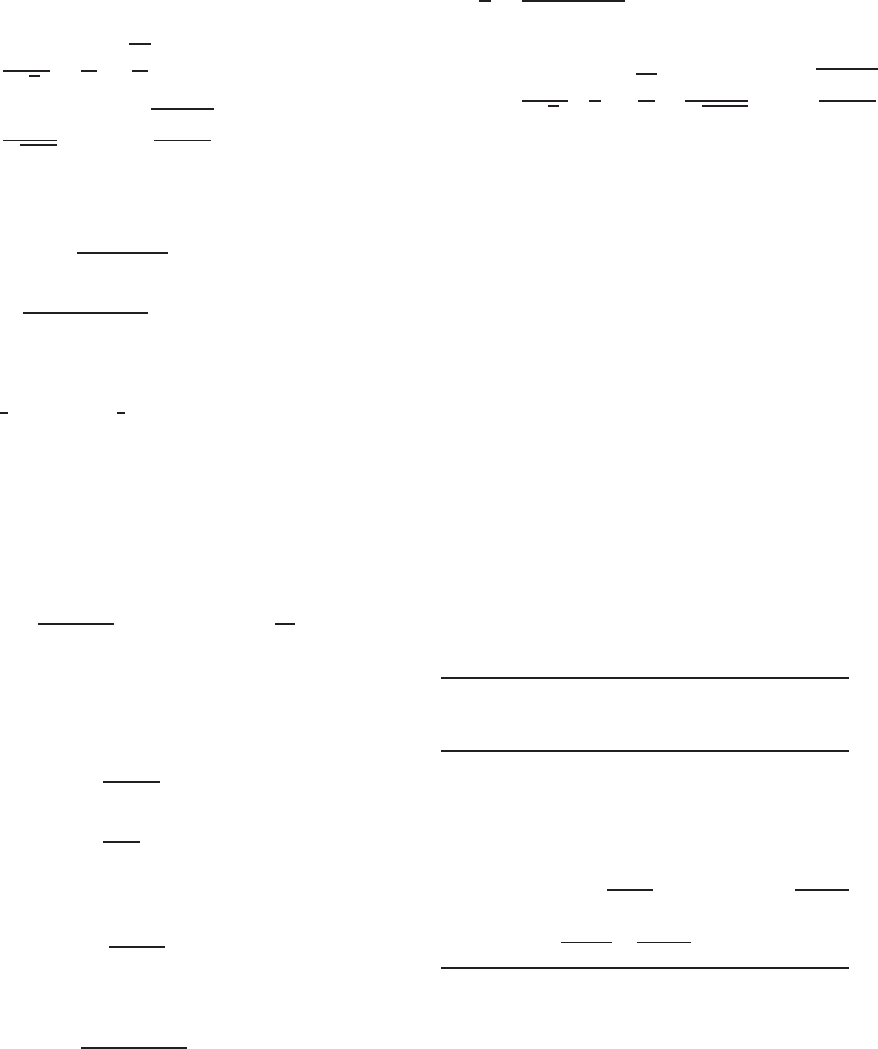
104 4 FLEXURAL MEMBERS

Since D/w<0.25 and θ = 90

◦

for the simple lip

edge stiffened, from Table 3.5

k = 3.57(R

)

+ 0.43

= 3.57(0.206)

1/3

+ 0.43 = 2.54 < 4.0OK

Use k = 2.54 to calculate the plate slenderness

factor for the compression ﬂange as follows:

λ =



1.052

√











1.052

√

2.54



(42.17)



29,500

= 1.146 > 0.673

The effective width of the compression ﬂange is

b = ρw =



1 − 0.22/λ





1 − 0.22/1.146

1.146



(3.1624) = 2.230 in.

From Eqs. (3.77) and (3.78),





(b)(R

) =



×2.230



(0.206) =0.230 in.

= b − b

= 2.230 − 0.230 = 2.00 in.

iii. Reduced Effective Width of the Edge Stiffener. The

effective width of the edge stiffener under a stress

gradient can be determined according to Section

3.5.2.2. From Eq. (3.64),

k =

0.578

ψ +0.34

where ψ =



In the above equations, the compression stresses f

and f

(Fig 4.5b) are calculated on the basis of the

gross section as follows:

= 50



4.8312

5.0



= 48.312 ksi

= 50



4.28

5.0



= 42.80 ksi

Therefore

ψ =



42.80

48.312



= 0.886

and

k =

0.578

0.886 + 0.34

= 0.471

The k value of 0.471 calculated above for the

edge stiffener under the stress gradient is slightly

larger than the k value of 0.43 for unstiffened

elements under uniform compression.

The effective width of the edge stiffener can be

determined as follows:

D − (R + t)

= 7.35

f = f

= 48.312 ksi

λ =

1.052

√







1.052

√

0.471

(7.35)



48.312

29,500

= 0.456 < 0.673

ρ = 1.0

The effective width of the edge stiffener is



= d = 0.551 in.

The reduced effective width of the edge stiff-

ener is

= d



) = 0.551(0.206) = 0.113 in.

The above calculation indicates that the compres-

sion stiffener is not fully effective.

iv. Location of Neutral Axis and Computation of I

and S

a. Location of Neutral Axis Based on Full Web

Element. Assuming that the web element

(element 7 in Fig. 4.6) is fully effective,

the neutral axis can be located by using the

following table. See Fig. 4.6 for dimensions of

elements.

Effective Distance from

Length Top Fiber Ly

Element L (in.) y (in.) (in.

)

1 0.5512 9.5556 5.2670

2 2(0.206) = 0.4120 9.9148 4.0849

3 3.1624 9.9625 31.5054

4 2(0.206) = 0.4120 0.0852 0.0351

5 2.2300 0.0375 0.0836

6 0.1130 0.2254 0.0255

9.6624 5.0000 48.3120

Total 16.5430 89.3135



(Ly)



89.3135

16.5430

= 5.399 in.

Use Section 3.5.1.2 in this volume or Section

B2.3 of the North American Speciﬁcation to

check the effectiveness of the web element.