Зазуляк П.М., Гавриш В.І. Євсєєва Е.М., Йосипчук М.Д. Основи математичного опрацювання геодезичних вимірювань
Подождите немного. Документ загружается.


Методи врівноваження багатьох виміряних величин З і
Як видно з формул (5.51), для того, щоб отримати числове значення eej
т або ji, потрібно мати суму [v
2
] або
[pv
2
].
Є кілька способів обчислення нав
сум. Розглянемо ці способи.
Перший спосіб полягає у безпосередньому їх обчисленні, тобто розв'5
нормальну систему поправок відносно т. (у' = 1,л) одним із раніше нав
методів, отримаємо числові значення
v.
(і
=
1 ,п) зі системи параметричних f
поправок (5.13), після чого знаходимо суму [v
2
] або [pv
2
].
Для обчислення наведених сум другим способом, використаємо рівно
[pv
2
] = \plv], [v
2
] = [/v], (
справедливість яких покажемо на прикладі нерівноточних вимірювань. Длі
розглянемо матричне параметричне рівняння поправок (5.17)
At+L = V,
яке ліворуч домножимо на VP
VPAr + VPL = VPV
та отриманий результат протранспонуємо
(VPA т + VPL)
T
= (VPV)
7
.
У результаті отримаємо
т
Т
А
T
PV+ L
T
P V = VPV.
Але оскільки A
T
PV = 0 (див. рівність (5.20)), то отримане співвіднс
набуде вигляду
L
T
PV= VPV,
яке запишемо в розгорнутому вигляді
(/і,/
2
,...,/„
Рх 0
0 Р
2
v
•
J
V
"У
= (v,
v
2>
о о - р
п
або, перемноживши ліву та праву частини
О
Рі
0
0 Р
2
0 0
0
0
Рп
О
V
п
)
(l\Pu hPn КРп)
'У ^
= (v,
Рх,
v
2
p
2
, ..., v
nPn
)
V
V
V

314
Розділ V
приидемо до рівності
+ l
2
p
2
v
2
+ ... + /д
Л
= v^v, + v
2
p
2
v
2
+ ... + уду„,
тобто
[/pv] = [v
2
p].
Отже, для нерівноточних вимірювань справедливість рівності [pv
2
] = [plv] є
доведеною. Аналогічно можна показати і справедливість рівності [v
2
] = [lv] для
рівноточних вимірювань.
Третій спосіб обчислення наведених сум полягає у використанні таких
рівностей:
[pv
2
]
= [pal]
• т,
+ [pbl]
• т
2
+... + [pul]
•
т
к
+[р1
2
],
(5.54)
[v
2
]=[al]-r
l
+[ЬІ]-т
2
+... + [иІ]-т
к
+[/
2
].
Для доведення, наприклад, першої рівності, розглянемо матричне параметричне
рівняння поправок (5.17)
АТ+ L= V,
яке протранспонуємо
(АТ + L)
T
= F
7
" => Т
Т
А
Т
+ L
T
— V
та домножимо отриманий результат праворуч на PV
R
T
A
T
PV + ІІ PV = V
T
PV => T
T
A
T
P-(AT + L) + L
T
P-(AT + L) = V
T
PV =>
Т
Т
А
Т
РА T + Т
T
A
T
PL + L
T
PAR + +L
T
PL = V
T
PV => Т
Т
•
(A
T
PA Т + A
T
PL) +
+ L
T
PAR + L
T
PL = V
T
PV.
Оскільки A
T
PAR+ A
T
PL = NT + В =
0
- матричне нормальне рівняння поправок,
то остаточно рівність перепишемо
L
T
PAT + L
T
PL = V
T
PV,
(5.55)
або в розгорнутому вигляді
І2, К)
р
х
0 ... о
0 р
2
... о
о о
Рп
а
х
Ь
х
а
2
Ь
2
а
п
Ь
п
f
- \
+
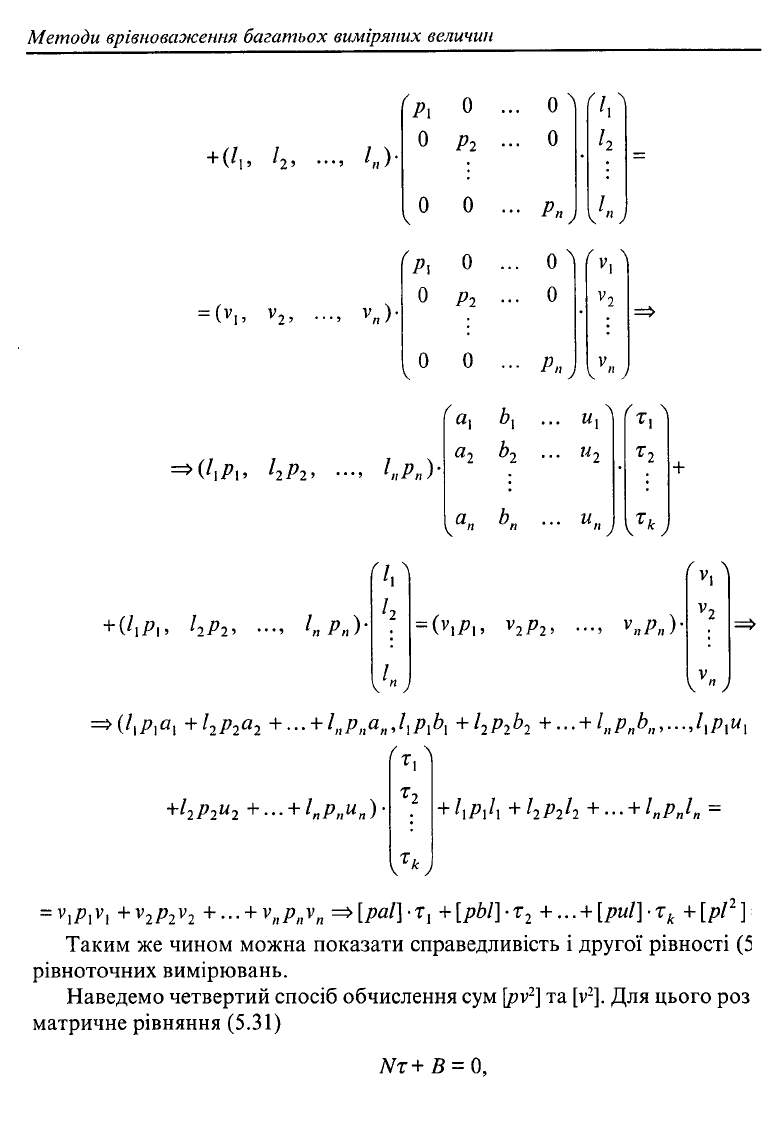
Методи врівноваження багатьох виміряних величин З і
+ (/,, /
2
, ..., /„)
= (
v
l>
v
2>
(/,/?,, l
2
p
2
, ..., l„p„)
/
Рі
0 ... 0
0
Р2
... 0
0
V
0
••• Рп
(Рі
0
... 0
0
Р2
... 0
0
V
0
••• Рп
ч
Ь, ...
А, Ь
7
...
V У
+
v
*
у
// \
'v.
N
(hPi, V
2j
p
2
, ..., v„/>„)
(l\P\
a
\ +l
2
P2
a
2 +
•••
+ lnPn
a
n>
l
\PA +
l
lP2
b
2 +
•••
+
l
„Pn
b
„>--->
l
\P\
U
\
+l
2
p
2
u
2
+ ... + l„p„u
n
)
T
/t
V У
+ Wl +hP2
l
2+~- + l
n
Pjn =
= v,p,v, +V
2
p
2
v
2
+... + v
nj
p„v
n
=>[/w/]-T, +bW]-T
2
+ ... + [ри/]-т* +[p/
2
]
Таким же чином можна показати справедливість і другої рівності (5
рівноточних вимірювань.
Наведемо четвертий спосіб обчислення сум \pv
2
] та [v
2
]. Для цього роз
матричне рівняння (5.31)
Nr+B = Q,
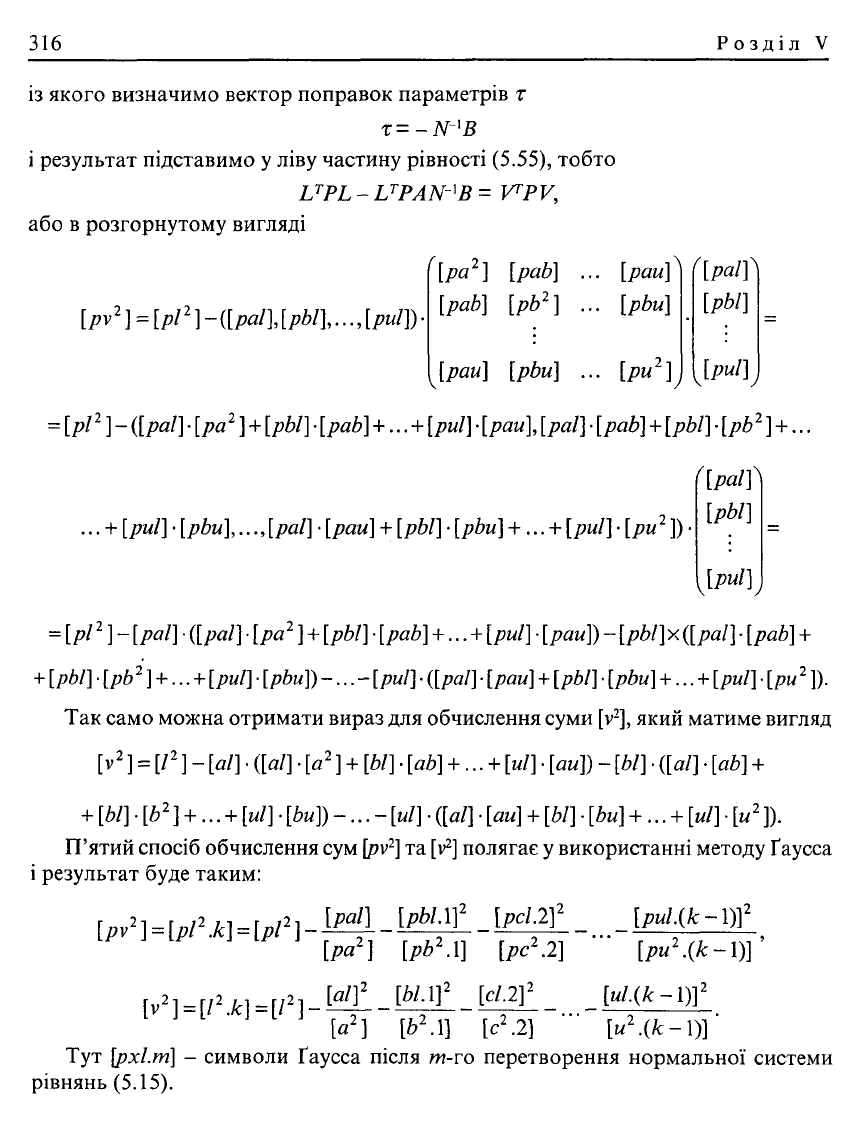
316 Розділ V
із якого визначимо вектор поправок параметрів т
т = - N~
l
B
і результат підставимо у ліву частину рівності (5.55), тобто
L
T
PL - L
T
PAN
]
В = VPV,
або в розгорнутому вигляді
ґ
[ра
2
] [pab] ...
[pab] [pb
2
] ...
[pv
2
] = [pl
2
]-{[pal],[pbl],...,[pul])
[рай]
[pbu]
[pau] [pbu] ... [pu
2
]
[pal]
[pbl]
[pul]
= [pl
2
\~ ([pal]
•
[pa
2
]
+ [pbl]
•
[pab] +... + [pul]
•
[pau], [pal]
•
[pab] + [pbl] -[pb
2
] + ...
... + [pul]
•
[pbu],...,[pal]
•
[pau] + [pbl]
•
[pbu] +... + [pul]
•
[pu
2
])
[pal]"
[pbl]
[pul]
~[pl
2
]
~ [pal]
•
([pal]
•
[pa
2
]
+ [pbl]
•
[pab] +... + [pul]
•
[pau]) - [pbl] x ([pal]
•
[pab] +
+ [pbl] -[pb
2
]
+ ... + [pul]
•
[pbu]) -... - [pul]
•
([pal]
•
[pau] + [pbl]
•
[pbu] +... + [pul]
•
[pu
2
]).
Так само можна отримати вираз для обчислення суми [v
2
], який матиме вигляд
[v
2
]
= [І
2
]
~ [аі]
•
([аі]
•
[а
2
]
+ [bl]
•
[ab] +... + [иі]
•
[аи]) - [bl]
•
([аі]
•
[ab] +
+ [bl]
•
[b
2
]
+ ... + [ul]
•
[bu]) -... - [ul]
•
([al]
•
[au] + [bl]
•
[bu] +... + [ul]
•
[u
2
]).
П'ятий спосіб обчислення сум [pv
2
] та [v
2
] полягає у використанні методу Ґаусса
і результат буде таким:
[pal] [pbl.l]
2
[pcl.2]
2
[pul.(k-l)]
2
[pv
2
] = [pl
2
.k] = [pl
2
]-
[v
2
] = U
2
.k] = [l
2
]-
[ра
2
] [pb
2
.1] [рс
2
.2]
[al]
2
[bl.\]
2
[cl.2]
2
[pu
2
.(k-1)]
[ul.(k -1)]
2
[a
2
] [b
2
.l] [c
2
.2] [u
2
.(k-1)]'
Тут [pxl.m] - символи Ґаусса після m-го перетворення нормальної системи
рівнянь (5.15).

Методи врівноваження багатьох виміряних величин З і
Визначивши одним із наведених способів суму [pv
2
] або [v
2
], та підстави
у формули (5.51), (5.52), отримаємо значення середньої квадратичної похи
для одного рівноточного вимірювання або середню квадратичну похибку оj
ваги
ju
для нерівноточного вимірювання.
Часто на практиці необхідно знати середні квадратичні похибки ф;
виміряних величин: висот реперів, координат пунктів, довжин ліній, дирекі
кутів. Для цього спочатку потрібно визначити ваги цих функцій. При застос
параметричного методу врівноваження аргументами таких функці
називаються ваговими, зручніше вибирати не виміряні величини, а в
параметри.
Тому перейдемо до оцінки точності наближених елементів за допо
вагової функції, яку в загальному випадку подамо у вигляді
F=F(t
v
t
v
...,t.)
к"
(
де t. (j = 1,к) - врівноважені значення параметрів.
Оскільки вагова функція (5.56) може бути складною, то лінеаризуємо
як врівноважені значення параметрів можна виразити через їх наближені зн
та поправки, а саме
t:
• J .j..j,j = l,k,
то в околі точки
,
t
2
,
•
•t\) функцію F- F{t
v
t
2
,..., t
k
) розкладемо в ряд Тс
припустивши, що це можна зробити. Обмежившись лінійними членами ро
1
у результаті отримаємо
F~F(t?,t
0
2
,...,t
0
k
)+Z
М
aF
dt j
V
7
У
•
Т
7
Введемо позначення для значень часткових похідних
/ ^ л
ар
dt,
функціїFв точці {t
x
,tl,...,tl)
j
F(t
x
,t
2
,-..,t
k
)
—
F
0
,
j = l,k та
'dF
Л
dt,
= W = \,k).
Значення часткових похідних вагової функції F в точці (/f,/®
величиниf.(j
= \,к), що виражаються рівностями (5.58), називаються коефіо
вагової функції F.

318
Розділ V
Після введених позначень вираз (5.57) для вагової функції ^запишемо у вигляді
F = F
0
+ if
j
-x
j
. (5.59)
7=1
Вагу наведеної функції визначити за формулою (4.65) не можна, оскільки вона
є справедливою для незалежних вимірювань, а у нашому випадку аргументи
т.
(j = 1 ,к) функції F, в результаті врівноваження стають залежними, так як даний
процес здійснюється при умові [v
2
]—шіп або
\pv
2
]—>min.
Тому спочатку функцію F,
подану виразом (5.59), потрібно виразити через незалежні аргументи, а для цього її
зобразимо у вигляді
F = F
0
+ Іfj
• тj
+ ([а
2
] •
т, + [ab]•
т
2
+... + [аи]• х
к
+ [а/])• q
x
+ ([аб]-т, + [Ь
2
]-т
2
+...
7=1
... + [Ьи]-т
к
+[bl])-q
2
+ ... + ([аи]-т, +[Ьи]-т
2
+ ... + [u
2
]-r
k
)-q
k
, (5.60)
де q. (j = 1 ,к) - неозначені коефіцієнти.
Із наведеного зображення функції F видно, що до виразу (5.59) приєднано
рівняння нормальної системи (5.16), помножені на неозначені коефіцієнти
<?
;
. С/ = 1,£) відповідно.
У виразі (5.60), розкривши дужки та звівши подібні члени при т. (j = l,k),
отримаємо
F = F
0
+ [al]
•
q
x
+[bl]-q
2
+ ... + [«/]• q
k
+([a
2
]-^r, + [ab]
•
q
2
+ ... + [au]
•
q
k
+ /,)
•
T
t
+
+ {[ab]-q
{
+[b
2
]-q
2
+... + [bu]-q
k
+/
2
)-т
2
+...+
+ {[au]-q
x
+[bu]-q
2
+... + [u
2
]-q
k
+f
k
)-T
k
. (5.61)
А тепер неозначені коефіцієнти q. (j = \,k) підберемо так, щоб вирази у круглих
дужках співвідношення (5.61) дорівнювали нулеві.
Тоді вагову функцію F можна записати так:
F=F
0
+ [al]
•
q
x
+ [bl] -q
2
+... + [ul]
•
q
k
. (5.62)
Із наведено виразу для функції F видно, що вона виражена через величини
І, -/Ж
к
) -
Xj
(і = 1,п) (див. формули (5.12)), які є незалежними, оскільки
/•(ґ,
0
,t
2
,...,tl)- const (і = 1,«), а результати вимірювань х
(
(/ = 1,«) спостерігачі
стараються отримати незалежними і тому для неї можна застосувати формулу
(4.65), щоб визначити її обернену вагу. Для простоти викладу вважатимемо, що
вимірювання є рівноточними, тобто = 1(г =
1,
п) і тоді формула (4.65) запишеться
у вигляді

Методи врівноваження багатьох виміряних величин
P
F
її
д1
і
V
1
(5.63)
Вираз (5.62) запишемо в розгорнутому вигляді та знайдемо часткові
^(і = \,п) функції
о/.
F = F
0
+ 2 (а,/,)
•
q
x
+ І
(Ь,1,) •
q
2
+ ... + І (и,// )•</,,
<•=і /=і /=і
&F
а/,
А
— = a
2
q
x
+b
2
q
2
+... + u
2
q
k
о/,
Згідно формули (5.63), отримані вирази для часткових похідних_підне
квадрату та просумуємо, додавши та віднявши величини / . -q
•
(j = \,k) від
Згрупувавши подібні члени та використавши співвідношення (5.63), одерз
1
— = {[«]•#! +[ab]-q
2
+... + [au]-q
k
+ /,}•?, +
"f
+ {[ab]-q
l
+[b
2
}-q
2
+... + [bu]-q
k
+/
2
}-q
2
+...
2
k
+ {[au]-q, +[bu]-q
2
+... + [u ]-q
k
+f
k
}-q
k
- 1/j •qj.
>i
Оскільки у наведеному співвідношенні вирази у фігурних дужках спів:
із виразами у круглих дужках співвідношення (5.61), які дорівнюють н
приходимо до остаточної формули, яка служить для визначення оберне
функції F врівноважених значень параметрів t. (j = l,k)
1 * ,

320
Розділ V
Множники q. (j = l,k) називаються перехідними коефіцієнтами і їх можна
визначити із такої нормальної системи рівнянь:
[я
2
] 'Ч\ +[ab]-q
2
+... + [au]-q
k
+/, =0
[ab]-q
l
+ [b
2
]-q
2
+... + [bu]-q
k
+ f
2
= 0
(5.65)
[au]-q
x
+ [bu]-q
2
+... + [u
2
]-q
k
+ f
k
=0.
Для нерівноточних вимірювань формула для знаходження оберненої ваги
функції F (5.64) залишається незмінною, а нормальна система для визначення
перехідних коефіцієнтів запишеться у вигляді
[pa
2
]-q
l
+ [pab]-q
2
+ ... + [раи]-q
k
+/, =0
[pab]-q
{
+[pb
2
]-q
2
+ ... + [pbu]-q
k
+ f
2
=0
(5.66)
W'?| +[pbu]-q
2
+... + [pu
2
]-q
k
+f
k
=0.
Якщо для розв'язування нормальних систем (5.65) або (5.66) застосувати метод
Ґаусса і отримані вирази для q. (j = 1,к) підставити у формулу (5.64), то отримаємо
співвідношення для визначення оберненої ваги функції F через величини
f.(j
= \,к)
та символи Ґаусса для рівноточних вимірювань
1 /,
2
, [Л.1]
+
-
P
F
[a
2
] [b
2
1]
+... +
[Л.(^-І)]
2
[и
2
(к-1)]
та нерівноточних вимірювань
1
/,
2
+
[ЛІ]
2
+ ... +
[Л.(^-І)]
2
(5.67)
(5.68)
P
F
[pa
2
] [pb
2
1] [ри
2
{к-\)]
Таким чином, другий пункт задачі знаходження оцінки точності результатів
врівноваження параметричним методом, а саме оцінка точності наближених
елементів за допомогою вагової функції, є виконаним, тобто є розрахункові
формули (5.64), (5.67), (5.68) для обчислення оберненої ваги функції врівноважених
значень параметрів.
Наведемо ще одне співвідношення для визначення оберненої ваги функції
врівноважених значень параметрів через вагові коефіцієнти. Для цього розглянемо
нормальну систему рівнянь (5.65) для визначення перехідних коефіцієнтів
q. (j- \,к) у випадку рівноточних вимірювань, яку запишемо у матричному
вигляді

Методи врівноваження багатьох виміряних величин З і
N-q +/= 0.
(5.69)
Тут N =
#2
(
[а
2
] [ab] ...[ои]
л
[ab] [b
2
]...[bu]
[аи] [bu]...[u
2
]
матриця коефіцієнтів нормальної системи;
невідомий вектор перехідних коефіцієнтів;
/ =
/2
Л
- вектор коефіцієнтів вагової функції F.
Припустивши, що det/V* 0, розв'язок матричного нормального рівняння (5.69
згідно формули (5.32), запишеться у вигляді
-q = N~
l
-f. (5.70)
Для знаходження оберненої матриці Q = ./V
4
використаємо тотожність
NQ = Е,
де Е- одинична матриця.
<2,2 ... Є,
Л
Невідомі елементи матриці Q =
Сік
Qn Q22 ••• Q.
2к
Qki Qk2 - Q,
розв'язавши к матричних нормальних рівнянь
ґ г> \
N-
Qu
Q21
y
Qkl;
о
V У
N'
Q22
yQk2
ґп\
0
о
v у
кк
f Г\ \
можна отримати
>•••) N •
Qik
Q2k
vQ-y
0
1
V У

322
Розділ V
Слід відзначити, що оскільки матриця N є симетричною, то буде симетричною
і матриця Q, тобто Q
tj
= Q
fi
(i,j = \,k).
Розв'язавши к наведених матричних нормальних рівнянь, одержимо шукані
елементи матриці Q.
Тоді співвідношення (5.70) можна записати так:
-<7 = 6/ (5.71)
або в розгорнутому вигляді
-Qj = i.Qji-fi, J = U.
і=і
У даному випадку матриця Q називається ваговою матрицею, а її елементи
Qij (і, j = 1 ,к) - ваговими коефіцієнтами.
Підставивши вираз (5.71) у формулу (5.64), отримаємо співвідношення для
визначення оберненої ваги функції врівноважених значень параметрів через вагові
коефіцієнти
~
р
r = f
T
'Q-f• (5-72)
"f
Наведену формулу (5.72) запишемо в розгорнутому вигляді
= І fj • IQJI •/,=/, (QnA + 6,2/2 + - + Qikfk) +
r
F
j=1 /=1
+ /2(62./. +622/2 +- + б2*Л) + - + Л(Є*і/і +6.2/2 +- + Є**Л) =
= 6„/.
2
+2612/1/2 +... + 2QM +Q
22
f
2
2
+... + 1Q
2k
f
2
f
k
+ flQ
kk
.
Якщо вимірювання будуть нерівноточними, то матриця коефіцієнтів
нормальної системи буде такою:
/ 2 \
[pa ] [pab]... [рай]
N=
[pab] [pb
2
]...[pbu]
[pau] [pbu]...[pu
2
]^
Залишився нерозв'язаним останній пункт задачі врівноваження, а саме, якою
буде оцінка точності отриманих врівноважених параметрів.
Припустимо, що вагова функція F, подана у загальному випадку виразом
(5.56), має такий частковий вигляд:
