Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

или

+ |/

5Г

р2

6OK

(5-75)

Задана ширина главного лепестка 2&

; параметр z

определяется по формуле

cos

•

2М

(5-76)

В первом случае получающуюся ширину основного

лепестка на нулевом уровне можно определить из фор-

мулы (5-76); во втором случае уровень бокового излуче-

ния определяется из формулы (5-74).

По известному параметру z

находятся амплитуды

токов в излучателях:

для четного Q=2N по формуле

- = J](-1>

(2N—\)(q + N —

2)l

(q-n)\(q + n-\)\(N-q)\

-; (5-77)

q—n

для нечетного

= 2 N

-{-

но формуле

'n=J](-l)

N-q 2q

ZQ '

2N{q + N — 1)1

(<?

n)!

(<?

n)!

(A/

- qy

(5-78)

Результаты расчетов, выполненных при различных чис-

лах излучателей (от 4 до 144) при заданном уровне боко-

вого излучения £бок и при расстоянии между излучате-

лями d^Y' приведены в (ЛО. 1]. Там же приведена

величина g—-отношение коэффициента усиления рас-

сматриваемой решетки к коэффициенгу усиления такой

261

же равномерной решетки. Этот относительный коэффи-

циент усиления определяется формулами:

g= и

- четное; (5-79)

=• —-; —ц-^—г—, Q

—

нечетное. (5-80)

(2N+\)I /2+2 £ l\ \

Анализ полученных распределений токов показал, что

при числе излучателей, больших 20, амплитудные рас-

пределения, за исключением токов в крайних вибрато-

рах, хорошо аппроксимируются выражением

/(Е) = (С£

+Я£

+1)

, (5-81)

где С= ,

- •—относительная координата по оси решетки;

С = 0,0861 arcch ~ 0,228;

?вок

= 0,225 arcch ~ 0,24.

' «бок

Величины коэффициентов С и D могут быть взяты из

графиков, приведенных «а рис. 6-15,6. На основании

этой аппроксимации амплитудное распределение опти-

мальных линейных решеток с числом излучателей, боль-

шем 20, может быть рассчитано по формуле (5-81).

Амплитуды токов в крайних излучателях определяются

через токи

/JV-I

в предпоследних излучателях по форму-

лам:

;

* =

"-'ЁУ-в!«g-i) '

четное; (5

82)

= /yv

-' 2N{4-\) '

НеЧеТНОе

)

262

Для того чтобы ДН полученной решетки имела один

главный максимум, расстояние между излучателями d

не должно приближаться к длине волны и тем более не

может превышать ее.

Метод Дольфа позволяет в принципе рассчитать <при

данном числе излучателей оптимальную антенну сколь

угодно малых размеров, имеющую заданную ширину

ДН. Однако при расстояниях между излучателями,

меньших А/2, токи в них получаются несинфазными, а их

амплитуды тем больше, чем меньше расстояние d.

Осуществить такое распределение токов возможно толь-

ко на одной частоте, да и это практически очень трудно.

К тому же КПД такой антенны из-за больших токов

будет весьма низким. Поэтому находят применение

только синфазные оптимальные антенны с расстоянием

d, лежащим в пределах

|<</<Я. (5-84)

Оптимальными могут быть и решетки осевого и наклон-

ного излучения [Л. 3, А]. Однако так как расстояния

между излучателями в таких решетках малы

(cf^-j-

меньше), то токи в излучателях имеют большие ампли-

туды и сдвиги фаз. Поэтому такие решетки трудно

практически реализовать.

Рассмотренная Дольфом оптимизация ДН не являет-

ся единственно возможной. Действительно, в оценке

качества антенны существенную роль играет ее излуче-

ние в области боковых лепестков. Это излучение играет

особо важную роль для приемных антенн, так как оно

определяет помехозащищенность антенны и ее шумовую

температуру.

Излучение антенны в секторе боковых лепестков

можно характеризовать несколькими параметрами:

максимальным относительным уровнем боковых лепест-

ков |бок. средним уровнем бокового излучения £

ср

среднеквадратичным уровнем бокового излучения |

р.кв

[см.

формулы (1-36)

—

(1-38)].

Для рассматриваемого

случая эти соотношения можно записать в следующем

виде:

5бои = ''маис Щ)\ ?

р =

"° J

M "° .'

263

В этих формулах и

и и

— значения обобщенной коор-

динаты для первого нул'Я и границы ДН соответственно.

Выше были рассмотрены оптимальные по первому из

перечисленных параметров антенные решетки, часто

называемые Дольф-Чебышевскими. Аналогичным обра-

зом могут быть рассмотрены решетки, оптимальные по

другим параметрам.

С точки зрения помехозащищенности от нескольких

помех с хаотическими фазами и направлениями прихода

антенна должна обладать наименьшим среднеквадра-

тичным уровнем бакового излучения [ЛО. 2]. Рассмот-

рим поэтому возможность построения линейной решетки

излучателей, оптимальной по среднеквадратичному

уровню бокового излучения [Л. 5].

Выражение для ДН решетки ненаправленных излу-

чателей (5-65) представляет собой полином Фурье:

(и)

= V /„ cos -^~~ и, (5-85)

я = 1

где u = kd sin О.

Такой полином обеспечивает наилучшее (в смысле

наименьшего среднеквадратичного отклонения) прибли-

жение к заданной функции f(u), если амплитудные

коэффициенты (у нас токи в излучателях 1

) определя-

ются выражением

«о

(v)

cos

Т"—vdv. (5-86)

В нашем случае функция f(u) определяет форму главного

лепестка ДН:

F(u)=

(f(u)npvu<u

;

87)

\ 0 при и

< и < kd,

при этом

kd>K,

т. е. d> -~- .

Эта функция может быть подобрана так, чтобы

обеспечить наименьший среднеквадратичный уровень

бокового излучения при заданных N И Н

Для подбора оптимальной формы главного лепестка

можно использовать выражение для ДН, получающееся

264

после подстановки (5-87) в (5-85) и проведения сумми-

рования в подынтегральном выражении:

sin Л'(и — и) , sinN(u~{-v)

и — v '

гг

-|- и

sin—а—

sin—„—

dv.

(5-88)

Однако нахождение оптимальной функции f(u) из

(5-88),

которое может быть выполнено с помощью при-

ближенных методов вычисления интеграла, весьма тру-

доемко. Поэтому оптимальную функцию f(u) целесо

образно найти приближенно, основываясь на особен-

ности разложения '(5-85). Эта особенность заключается

в том, что при заданной форме и ширине главного

лепестка ток» в вибраторах зависят только от номера п

и не зависят от числа вибраторов в антенне. Поэтому,

если вычислить величины /„ для заданной ширины

главного лепестка по нулевому уровню щ для несколь-

ких характерных функций /(«), то, сравнивая между

собой величины отбрасываемых токов, можно указать

наиболее подходящую для рассматриваемого N форму

главного лепестка. В табл. 5-3 приведены формулы для

/« для четырех характерных форм главного лепестка

[Л.

5]. Определение среднеквадратичного уровня боково-

го излучения для выбранной f(u) при небольшом

УУ<10—12 следует производить непосредственно по рас-

считанной ДН. Для большого ./V оценку этого уровня

целесообразнее проводить, считая, что отброшенные

члены бесконечной суммы из /„cos и являются

независимыми случайными величинами. Тогда для

ёср.кв получается выражение [Л. 5]:

_M[F* (

)]_

Ко <

•^-fr(u)da-J^I

1 о п=\

Е'-

л=1

(5-89)

265

Таблица 5-3

Форма главного лепестка

и функция [(и)

Формула для /

Равномерный: { (и) =• 1

Косинусоидальный:

пи

f (и) = COS

2u„

Косинусквадратный:

ям

f(«) = co8»2JT

Треугольный:

f (в) =

1 2/1—1

'""" 2я

—1

sln

2 "°

/„ =

1 2и—1

_(2п

—1)

«^

, 2п—1

sin -—g—

'« г /9я, 1

(2—

»)[--(

)«s

Л 2я-1 \

'»

= (2^Л)*~ ^ -

cos

"Г

"»

5-4. РАСЧЕТ СВЯЗИ ИЗЛУЧАТЕЛЕЙ

С ПИТАЮЩЕЙ ЛИНИЕЙ

В линейных антеннах, состоящих из большого числа

излучателей, последние обычно возбуждаются от питаю-

щей линии по последовательной схеме (рис. 5-16). Для

получения требуемого амплитудного распределения

(как правило, симметричного) связь каждого излучате-

ля с линией должна быть вполне определенной. При

большом числе излучателей она оказывается достаточно

слабой. В этом случае отражения пренебрежимо малы,

и можно считать, что в питающей линии установился

режим бегущей волны. Мощность, отбираемая при этом

от линии t-м излучателем, характеризуется коэффициен-

том связи а;:

<Xi

'•

где Pi — мощность, излучаемая t-м излучателем;

Лтр — мощность, проходящая дальше по линии.

Для того чтобы допущение о согласовании пи-

тающей линии на всем ее 'протяжении хорошо оправ-

266

дывалось, излучатели должны возбуждаться хотя бы

с небольшим сдвигом фаз. В этом случае на входе

антенны почти все волны, отраженные от неоднородн з-

стей, создаваемых элементами связи, взаимно компен-

сируются, входное сопротивление антенны остается

близким к волновому сопротивлению питающей линии.

у"!

Pftode J

Тип пи-

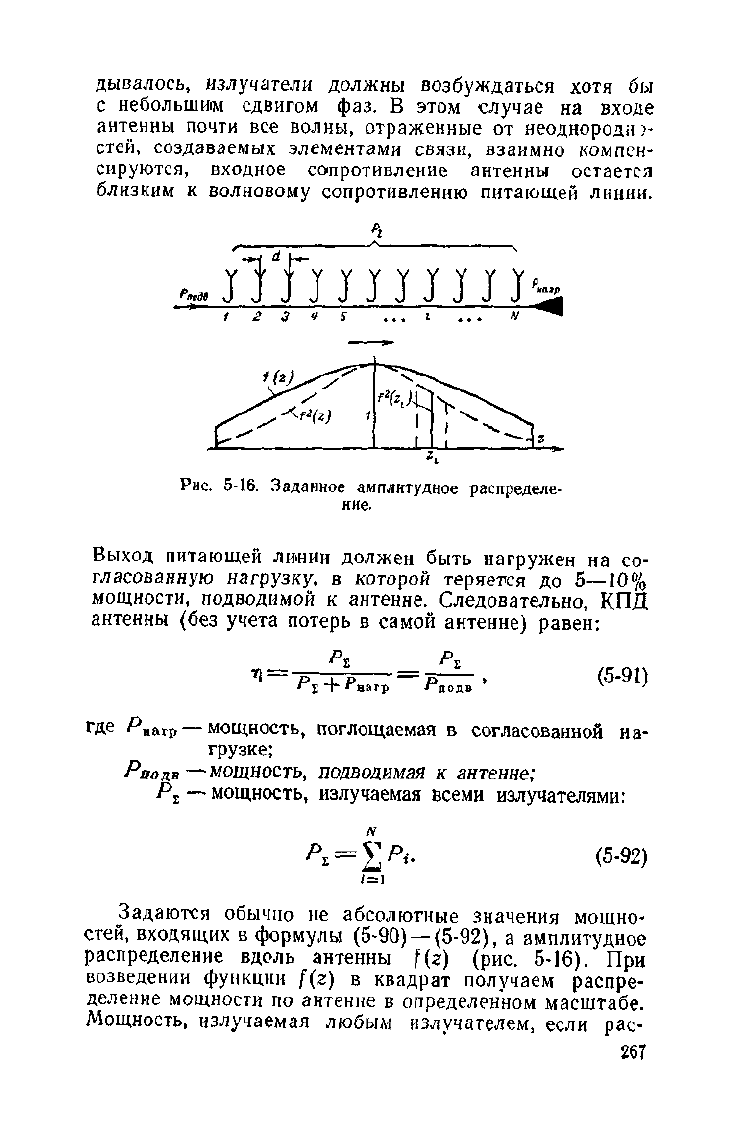
Рис.

5-16. Заданное амплитудное распределе-

ние.

Выход питающей линии должен быть нагружен на со-

гласованную нагрузку, в которой теряется до 5—10%

мощности, подводимой к антенне. Следовательно, КПД

антенны (без учета потерь в самой антенне) равен:

Р*

нагр

подв

(5-91)

где ^кагр — мощность, поглощаемая в согласованной на-

грузке;

Рдояв— мощность, подводимая к антенне;

— мощность, излучаемая всеми излучателями:

л=2/»*.

(5-92)

Задаются обычно не абсолютные значения мощно-

стей, входящих в формулы (5-90) —(5-92), а амплитудное

распределение вдоль антенны /(г) (рис. 5-16). При

возведении функции f(z) в квадрат получаем распре-

деление мощности по антенне в определенном масштабе.

Мощность, излучаемая любым излучателем, если рас-

26Т

стояние между излучателями равно d, пропорциональна

произведению

~f*\{z

)d. (5-93)

Для облегчения расчетов вводим понятие относительной

излучаемой мощности т

/под в

пропорциональное по (5-93)

ftizi):

Af*(z

Или для всей антенны

i=i /=i

(5-94)

(5-95)

(5-96)

Коэффициент пропорциональности А находим исходя из

энергетического баланса всей антенны:

V Pi ~~Г "нагр = ^Шодв,

i=l

отсюда

и, следовательно,

^^ /пода

1 = \

^тг^-ц.

(5-97)

Подставляя это значение Е/га* в выражение (5-96), нахо-

дим А и получаем окончательно:

пц = -ц-^

/'(*).

(5-98)

Таким образом, относипельные мощности т* легко

могут быть определены по заданному амплитудному рас-

пределению и заданному к. п. д. Если последний не

оговорен, то надо им задаться в пределах 90—95%,

268

Коэффициенты связи а,- определяются через т

;

действительно,

В общем виде

т^ а

/я

Яподв —Pi 1—/Я,

•и т. д. (5-99)

<*А

— («i + /И

• • •

+'Пк - О'

(5-100)

Зная (коэффициент связи aj и выбрав конструкцию

излучателей, можно рассчитать элементы связи.

'г-Н 1

ft'

0,05

__ j£W'

(г)

го зо ю 50 so 70 :о ЭР W

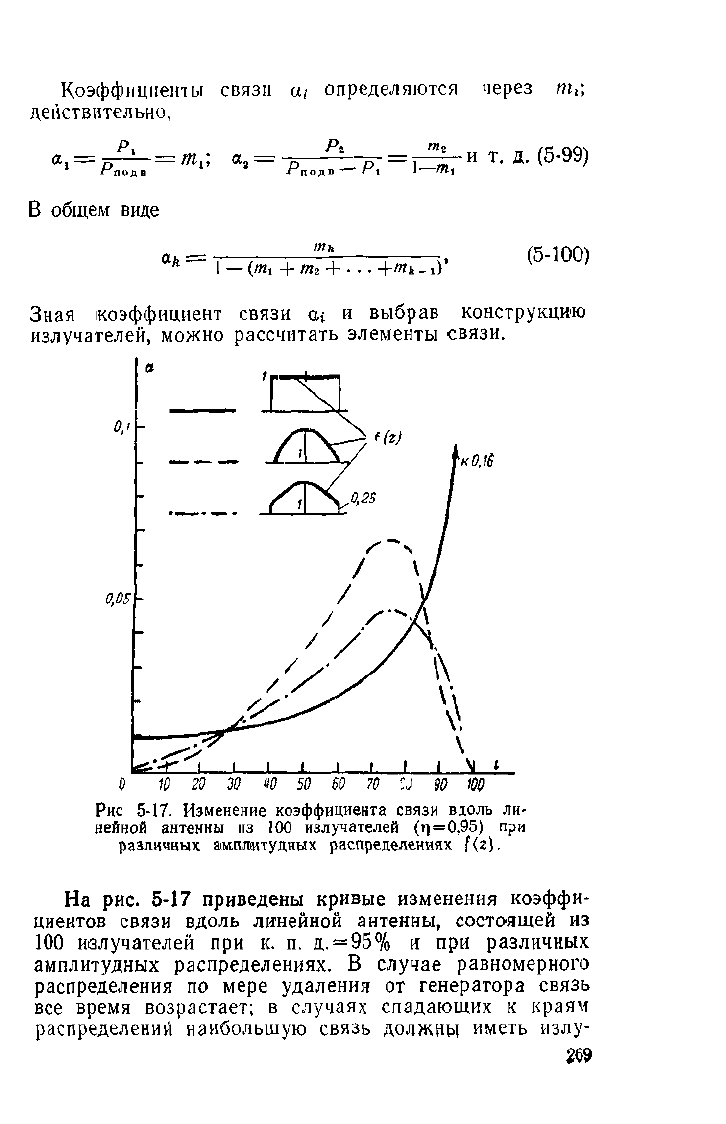
Рис 5-17. Изменение коэффициента связи вдоль ли-

нейной антенны из 100 излучателей

(г)

= 0,95) при

различных амплитудных распределениях \{г),

На рис. 5-17 приведены кривые изменения коэффи-

циентов связи вдоль линейной антенны, состоящей из

100 излучателей при к. п.

д.

95°/о

и при различных

амплитудных распределениях. В случае равномерного

распределения по мере удаления от генератора связь

все время возрастает; в случаях спадающих к краям

распределений наибольшую связь должны иметь излу-

269

чатели, расположенные где-то между серединой и кон-

цом антенны. Это объясняется тем, что по мере при-

ближения к концу антенны одновременно падают излу-

чаемая и подводимая к излучателям мощность.

При большом числе излучателей расчет можно про-

водить для групп, состоящих из 2—5 излучателей.

^U|iLqu[nqiiqiLqnJ[!iq[LJ[Q-

п)

ХД

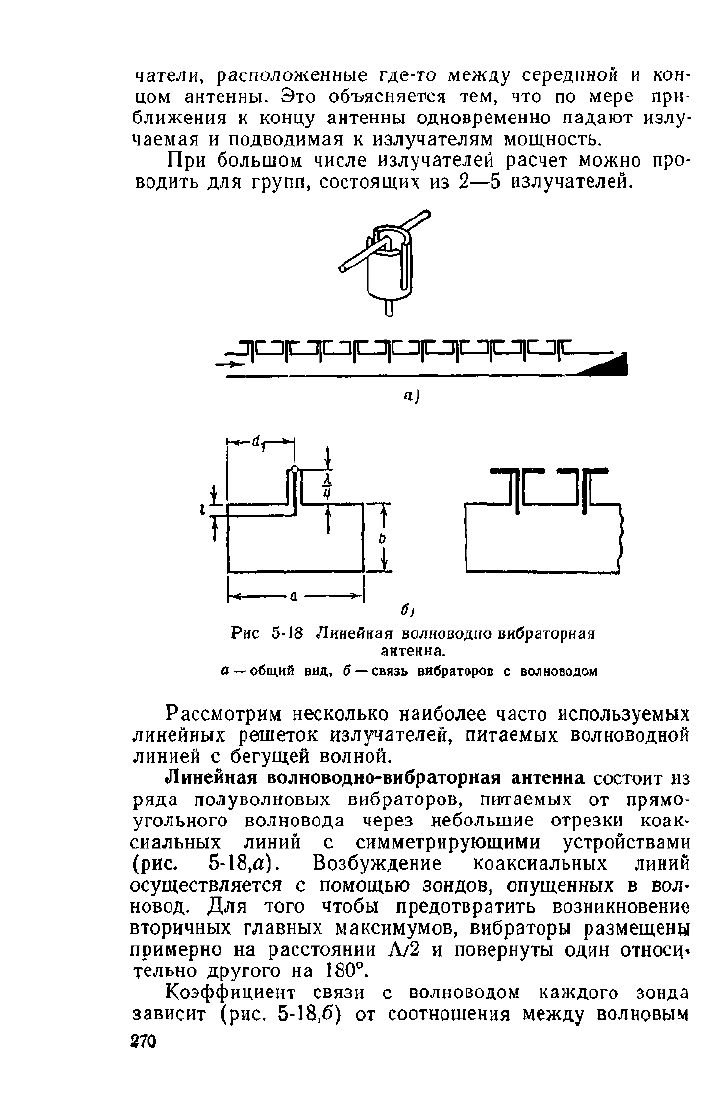
Рис 5-18 Линейная волноводно вибраторная

антенна.

—

общий вид, б — связь вибраторов с волноводом

Рассмотрим несколько наиболее часто используемых

линейных решеток излучателей, питаемых волноводной

линией с бегущей волной.

Линейная волноводно-вибраторная антенна состоит из

ряда полуволновых вибраторов, питаемых от прямо-

угольного волновода через небольшие отрезки коак-

сиальных линий с симметрирующими устройствами

(рис.

5-18,а). Возбуждение коаксиальных линий

осуществляется с помощью зондов, опущенных в вол-

новод. Для того чтобы предотвратить возникновение

вторичных главных максимумов, вибраторы размещены

примерно на расстоянии Л/2 и повернуты один относи-

тельно другого на 180°.

Коэффициент связи с волноводом каждого зонда

зависит (рис, 5-18,6) от соотношения между волновым

270