Zuo-Guang. Ye Advanced Dielectric Piezoelectric and Ferroelectric Materials: Synthesis, Characterisation and Applications

Подождите немного. Документ загружается.

Handbook of dielectric, piezoelectric and ferroelectric materials490

16.11

An infrared image of a ‘hard’ PZT rectangular plate driven at

the second resonance mode. Note the three hot points which

correspond to the nodal points for this vibration mode.

that both the ‘intensive’ dielectric and mechanical losses are composed of

the ‘extensive’ dielectric and mechanical losses, and that the extensive dielectric

loss tan δ changes significantly with the external electric field and stress, the

major contribution to the heat generation seems to come from the ‘extensive’

dielectric loss (i.e. 180° domain wall motion). Since this is just our model,

there can be different domain reorientation models, and further investigations

are waited for the microscopic observation of this phenomenon.

16.5 Loss anisotropy

Typically the specification sheet provided by the manufacturer gives only

one mechanical quality factor (Q

) and one dielectric loss tangent, which are

applicable only for the k

length extensional mode (i.e. imaginary parts of

and

, respectively). Losses can be, in general, introduced in the

complex material constants, where the real part indicates the usual material

constant and the imaginary part indicates the loss. As introduced in the

previous section in Fig. 6.3, in order to determine the loss tangent as a

tensor, the phenomenology for lateral (k

), longitudinal (k

), thickness (k

)

and shear (k

) modes has been repeated with complex material constants.

The theoretical thermodynamic analysis has been performed by considering

the intensive variables, stress and electric field (relating to generalized forces),

WPNL2204

Loss mechanisms and high-power piezoelectric components 491

and extensive variables, strain and electric displacement (relating to generalized

displacement), and four distinct phase angles, identified by their respective

free energies (denoted as Helmholtz loss tangent, Gibbs loss tangent, electric

Gibbs loss tangent and elastic Gibbs loss tangent). The data for the Gibbs

tangents for typical ‘soft’ and ‘hard’ piezoceramics (APC-850 and 841,

American Piezo Ceramics, PA) is presented in Table 16.2. The detailed

measuring technique and processes are reported in Ref. [5]. Note that the

(= 222) for the k

mode (imaginary part of

) is only 1/5 of that

(= 1087) for the k

mode (imaginary part of

This significant anisotropy in Q

reflects largely in designing the transducers

and transformers. Figure 16.12 exhibits an important example simulated for

a Rosen-type piezoelectric transformer, which includes both k

and k

mode

in one device. We adopted ATILA Finite Element Method software (ISEN,

distributed by Micromecharonics Inc., PA) for simulating a Rosen-type

piezoelectric transformer with 40 mm in length (see Fig. 16.12a). Figures

12(b) and 16.12(c) show admittance spectra simulated for an isotropic loss

condition (Q

= 1087) and for an anisotropic loss condition (Q

= 1087 and

222). As shown in the inserted magnified spectra, a half of the admittance

value at the peak is significant, as well as a slight resonance peak shift to a

lower frequency. Without knowing the peak admittance, it is difficult to

design a drive circuit for this transformer.

16.6 High-power piezoelectric ceramics

16.6.1 Very hard PZT-based ceramics

‘High power’ in this chapter stands for high-power density in mechanical

output energy converted from the maximum input electrical energy under

the drive condition with 20 °C temperature rise. For an off-resonance drive

condition, the figure of merit of piezo-actuators is give by the piezoelectric

d constant (∆L = dEL). Heat generation can be evaluated by the intensive

dielectric loss tan δ′ (i.e. P–E hysteresis).

In contrast, for a resonance drive condition, the figure of merit is the

vibration velocity v

, which is roughly proportional to Q

dEL. Heat generation

is originated from the intensive elastic loss tan φ′ (inverse value of Q

). The

mechanical power density can be evaluated by the square of the maximum

vibration velocity

()

, which is a sort of material constant. Remember that

there exists the maximum mechanical energy density, above which level the

piezoelectric material becomes a ceramic heater. High-vibration velocity

materials are suitable for actuator applications such as ultrasonic motors.

Further, when we consider transformers and transducers, where both

transmitting and receiving functions are required, the figure of merit will be

the product of v

k (k: electromechanical coupling factor).

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials492

Table 16.2

Gibbs loss tangents for typical ‘soft’ and ‘hard’ piezoceramics (APC-850 and 841, American Piezo Ceramics, PA)

Complex material APC850 (‘Soft Ceramic’) APC841 (‘hard ceramic’)

constant

Real part Imaginary part Loss tangent Real part Imaginary part Loss tangent

Elastic compliance (10

–12

/N)

16.9 –0.205 –0.012 2 11.4 –0.010 5 –0.000 92

–6.4 0.0779 –0.012 1 –3.42 0.003 83 –0.001 12

–5.6 0.067 –0.011 98 –5.65 –0.032 0.005 66

17.4 –0.347 –0.02 15.35 –0.069 2 –0.004 51

52.6 –3.82 –0.072 56 20.8 –0.24 –0.011 5

46.7 –1.968 –0.042 29.64 –0.028 –0.000 945

Dielectric constant (10

–9

F/m)

10.01 0.346 –0.0346 12 –0.048 –0.004

15.8 –0.34 –0.022 18 –0.162 –0.009

WPNL2204

Loss mechanisms and high-power piezoelectric components 493

Admittance magnitude

Load

(a)

Admittance magnitude (S)

40000 40800 41600 42400 43200 44000 44800 45600 46400 47200 48000

Frequency (Hz)

(b)

0.004573

0.004012

0.003451

0.00289

0.002329

0.001768

0.001207

0.000646

8.5e-05

Admittance magnitude (S)

0.003868

0.00365

0.003432

0.003214

0.00299

0.002778

0.00256

0.002342

0.002124

64600

64620

64640

64660

64680

64700

64720

64740

64760

64780

64800

Frequency (Hz)

Admittance magnitude (S)

40000 40800 41600 42400 43200 44000 44800 45600 46400 47200 48000

Frequency (Hz)

(c)

0.002624

0.002308

0.001992

0.001676

0.00136

0.001044

0.000728

0.000412

9.6e-05

Admittance magnitude (S)

0.002248

0.00217

0.002092

0.002014

0.001936

0.001858

0.00178

0.001702

0.001624

64600

64620

64640

64660

64680

64700

64720

64740

64760

64780

64800

Frequency (Hz)

0.0039

64.75 kHz

0.0022

64.71 kHz

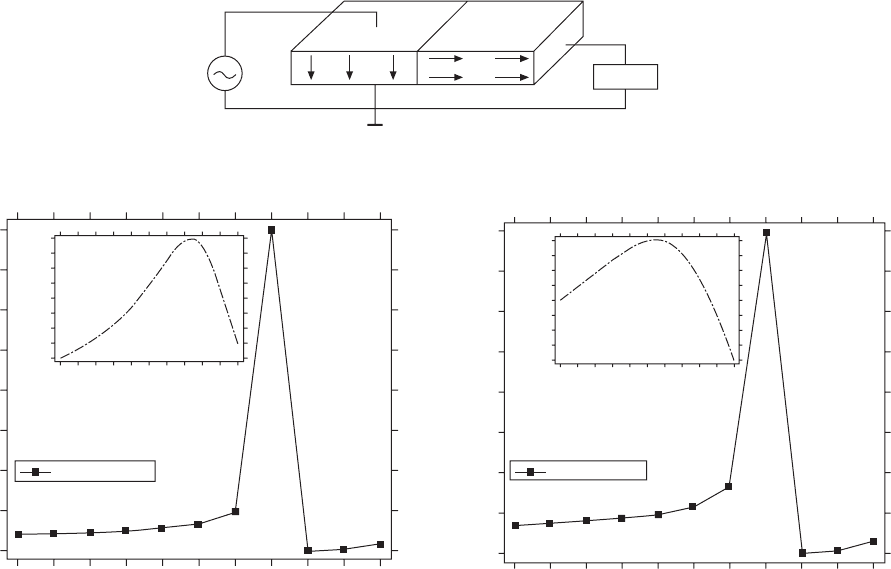
16.12

(a) Schematic structure of a Rosen-type piezoelectric transformer (40 mm in length); (b) admittance spectrum

simulated for an isotropic loss condition (

= 1087), and admittance spectrum for an anisotropic loss condition (

1087 and 222).

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials494

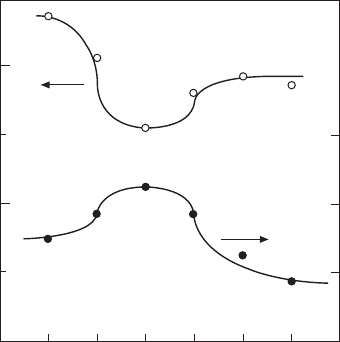
Let us discuss high-vibration velocity materials first. Figure 16.13 shows

the mechanical Q

versus basic composition x at two effective vibration

velocities v

= 0.05 m/s and 0.5 m/s for Pb(Zr

1–x

doped with 2.1 at.%

of Fe [12]. The decrease in mechanical Q

with an increase of vibration

level is minimum around the rhombohedral–tetragonal morphotropic phase

boundary (52/48). In other words, the smallest Q

material under a small

vibration level becomes the highest Q

material under a large vibration

level, and the data obtained by a conventional impedance analyzer with a

small voltage/power do not provide any information relevant to high-power

characteristics. Thus, we have developed various measuring techniques of

high-power piezoelectricity, including ‘constant current’ and ‘pulse drive’

methods [13].

Conventional piezoceramics have a limitation in the maximum vibration

velocity (v

max

), since the additional input electrical energy is converted into

heat, rather than into mechanical energy. The typical rms value of v

max

for

commercially available materials, defined by the temperature rise of 20 °C

from room temperature, is around 0.3 m/s for rectangular samples operating

in the k

mode (like a Rosen-type transformer) [10]. Pb(Mn,Sb)O

(PMS)–

lead zirconate titunate (PZT) ceramics with a v

max

of 0.62 m/s are currently

used for NEC transformers [12]. By doping the PMS–PZT or Pb(Mn,Nb)O

–

PZT with rare-earth ions such as Yb, Eu and Ce, we recently developed

high-power piezoelectrics, which can operate with v

max

up to 1.0 m/s [14,

15]. Compared with commercially available piezoelectrics, 10 times higher-

Mechanical quality factor

2000

1000

Mechanical Quality factor

Pb(Zr

1–

+ 2.1 at% Fe

Vibration velocity

= 0.05 m/s

= 0.5 m/s

600

400

200

0.48 0.50 0.52 0.54 0.56 0.58

Mole fraction of Zr (

)

16.13

Mechanical

versus basic composition

at two effective

vibration velocities

= 0.05 m/s and 0.5 m/s for Pb(Zr

Ti1–

doped

with 2.1 at.% of Fe.

WPNL2204

Loss mechanisms and high-power piezoelectric components 495

input electrical energy and output mechanical energy can be expected from

these new materials without generating a significant temperature rise, which

corresponds to 100 W/cm

. Figure 16.14 shows the dependence of the maximum

vibration velocity v

(20 °C temperature rise) on the atomic % of rare-earth

ion, Yb, Eu or Ce in the Pb(Mn,Sb)O

(PMS)–PZT-based ceramics.

Enhancement in the v

value is significant by adding a small amount of the

rare-earth ion [15].

16.6.2 Origin of high-power piezoelectrics

‘Hard’ PZT is usually used for high-power piezoelectric applications, because

of its high coercive field, in other words, the stability of the domain walls.

Acceptor ions, such as Fe

, introduce oxygen deficiencies in the PZT crystal

(in the case of donor ions, such as Nb

, Pb deficiency is introduced). Thus,

in the conventional model, the acceptor doping causes domain pinning through

the easy reorientation of deficiency-related dipoles, leading to ‘hard’

characteristics (domain wall pinning model [16]). In this section, we explore

the origin of our high-power piezoelectric ceramics.

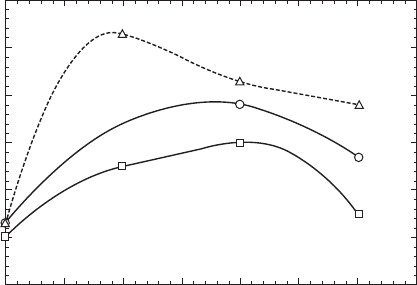
High mechanical Q

is essential in order to obtain a high-power material

with a large maximum vibration velocity. Figure 16.15 exhibits suggestive

results in the mechanical Q

increase with time lapse (minute) after the

electric poling measured for various commercial soft and hard PZTs, PSM–

PZT, and PSM–PZT doped with Yb. It is notable that the Q

values for

commercial hard PZT and our high power piezoelectrics were almost the

same, slightly higher than soft PZTs, and around 200–300 immediately

after the poling. After a couple of hours, the Q

values increased more than

Maximum vibration velocity (m/s)

1.1

1.0

0.9

0.8

0.7

0.6

0.5

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07

Doping concentration (atom ratio)

16.14

Dependence of the maximum vibration velocity

(20 °C

temperature rise) on the atomic % of rare-earth ion, Yb, Eu or Ce in

the Pb(Mn, Sb)O

(PMS)–PZT based ceramics.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials496

1000 for the ‘hard’ materials, while no change was observed in the ‘soft’

material. The increasing slope is the maximum for the Yb-doped PSM-PZT.

We also found a contradiction that this gradual increase (in a couple of

hours) in the Q

cannot be explained by the above-mentioned ‘domain wall

pinning’ model, but more likely by some ionic diffusion model.

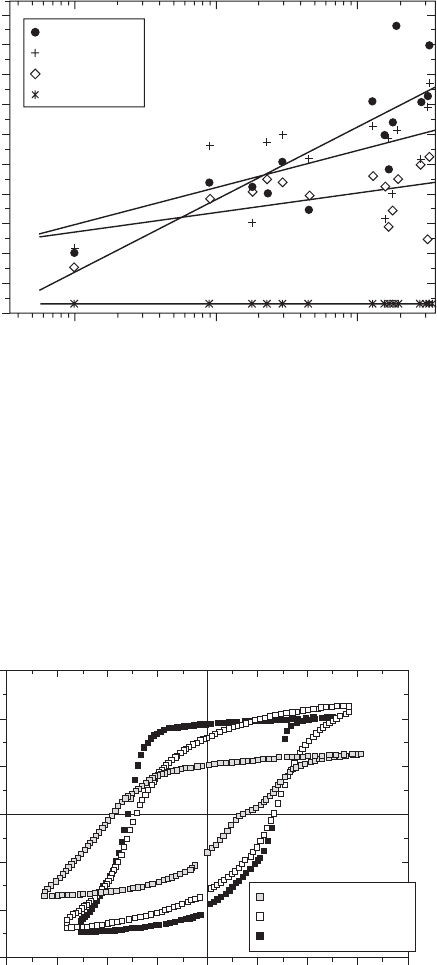
Figure 16.16 shows the polarization vs. electric field hysteresis curves

measured for the Yb-doped Pb(Mn,Sb)O

–PZT sample immediately after

PZT–PSM–Yb

PZT–PSM

Hard PZT

Soft PZT

2000

1800

1600

1400

1200

1000

800

600

400

200

10 100 1000

Time (min)

16.15

Change in the mechanical

with time lapse (minute) just

after the electric poling measured for various commercial soft and

hard PZTs, PSM–PZT, and PSM–PZT doped with Yb.

PZT–PSM–Yb fresh

PZT–PSM–Yb 48 h

PZT–PSM–Yb Aged

Polarization (C/m

)

0.3

0.2

0.1

0.0

–0.1

–0.2

–0.3

–40 –30 –20 –10 0 10 20 30 40

Electric field (kV/cm)

16.16

Polarization vs. electric field hysteresis curves measured for the

Yb-doped Pb(Mn,Sb)O

–PZT sample just after poling (fresh), 48 hours

after, and a week after (aged).

WPNL2204

Loss mechanisms and high-power piezoelectric components 497

poling (fresh), 48 hours after, and a week after (aged). Remarkable aging

effects could be observed: (a) in the decrease in the magnitude of the remnant

polarization and (b) in the positive internal bias electric field growth (i.e. the

hysteresis curve shift leftwards in terms of the external electric field axis).

The phenomenon (a) can be explained by the local domain wall pinning

effect, but the large internal bias (more than 1 kV/mm) growth (b) seems to

be the origin of the high-power characteristics. Suppose that the vertical axis

in Fig. 16.16 shifts rightwards, the inverse electric field required for realizing

the 180° polarization reversal is increased, leading to the resistance

enhancement against generating the hysteresis or heat.

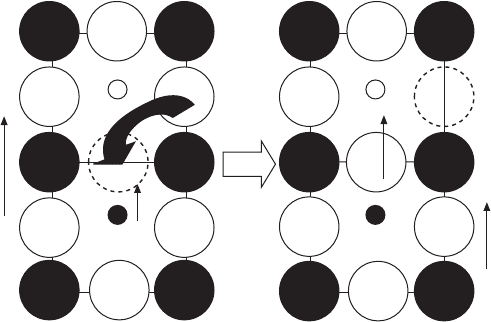
Finally, let us propose the origin of this internal bias field growth. Based

on the presence of the oxygen deficiencies and the relatively slow (a couple

of hours) growth rate, we assume here the oxygen deficiency diffusion model,

which is illustrated in Fig. 16.17. Under the electric poling process, the

defect dipole P

defect

(a pair of acceptor ion and oxygen deficiency) will be

arranged parallel to the external electric field. After removing the field,

oxygen diffusion occurs, which can be estimated in a scale of hour at room

temperature. Taking into account slightly different atomic distances between

the A and B ions in the perovskite crystal in a ferroelectric (asymmetric)

phase, the oxygen diffusion probability will be slightly higher for the downward,

as shown in the figure, leading to the increase in the defect dipole with time.

This may be the origin of the internal bias electric field.

16.6.3 Semi-hard PZT-based ceramics

Though the rare-earth doped PZT–Pb(Mn,Sb)O

system with the highest

vibration velocity satisfies actuator applications, due to relatively smaller

Diffusion

defect

Acceptor

16.17

Oxygen deficiency diffusion model for explaining the internal

bias electric field growth.

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials498

piezoelectric d constants, it cannot replace transducer or transformer materials,

where the direct piezoelectric effect is successively utilized to convert the

mechanical energy into final electrical energy. In this sort of electric–

mechanical–electric conversion application, since the figure of merit is v

we modified the composition to improve the high Q

by sustaining the high

d and k, starting from originally soft Pb(Zn

1/3

2/3

–Pb(Ni

1/3

2/3

–

Pb(Zr

0.5

. Sb, Li and Mn were substituted to the 0.8Pb(Zr

0.5

–

0.16Pb(Zn

1/3

2/3

–0.04Pb(Ni

1/3

2/3

ceramics. The composition

0.8Pb(Zr

1–d

–0.2Pb[(1–c){(1–b) (Zn

0.8

0.2

)

1/3

(Nb

1–a

)

2/3

–b(Li

1/4

(Nb

1–a

)

3/4

)}–c (Mn

1/3

(Nb

1–a

)

2/3

)]O

(a = 0.1, b = 0.3, c = 0.3 and

d = 0.5) showed the value of k

= 0.56, Q

= 1951 (planar mode), d

239 pC/N,

εε

= 739 and the maximum vibration velocity = 0.6 m/s at

31-mode. By adjusting the Zr/Ti ratio, compromised properties of k

= 0.57,

= 1502 (planar mode), d

= 330 pC/N,

εε

= 1653 and the maximum

31-mode vibration velocity = 0.58 m/s were obtained when Zr/Ti = 0.48/

0.52 [17]. These compositions are suitable for piezoelectric transformers and

transducers.

16.7 High-power piezoelectric components

Though we have developed ‘high-power density’ piezoelectric ceramics, the

multilayer structure is a key to developing actual ‘high-power’ components

from the device-designing viewpoint. However, the present Ag–Pd electrode

structure includes two problems: (1) expensive Pd and (2) although Ag

migration during sintering and under electric field applied can be suppressed

by Pd, the electrode conductance is significantly decreased. The latter is the

major problem in designing multilayer transformers, because the electrode

loss appears to be large, leading to heat generation and low efficiency. In

order to solve the problems, pure Cu electrode will be a key. But, the multilayer

samples need to be sintered at a relatively low temperature (90 °C or lower)

in a reduced atmosphere, when utilizing Cu embedded electrodes. Thus, it is

necessary to develop low-temperature sintering of ‘hard’ type PZTs. Unlike

soft PZTs, most of the conventional dopants to decrease the sintering

temperature failed to be used, because these dopants also degrade the Q

value significantly.

We further modified our high-power piezoelectric ceramics, the Sb, Li

and Mn-substituted 0.8Pb(Zr

0.5

–0.16Pb(Zn

1/3

2/3

–0.04Pb(Ni

1/3

2/3

, by adding CuO and Bi

in order to lower the sintering temperature

of the ceramics. Table 16.3 summarizes piezoelectric properties of semi-

hard piezoelectric ceramics based on Pb(Zn

1/3

2/3

–Pb(Ni

1/3

2/3

–

Pb(Zr

0.5

, sinterable at 900 °C. Under a sintering condition of 900 °C

for 2 h, the properties were k

= 0.56 Q

(31-mode) = 1023, d

= 294 pC/N

/ε

= 1282 and tanδ = 0.59%, when CuO and Bi

were added 0.5 wt%

each. The maximum vibration velocity of this composition was 0.41 m/s.

WPNL2204

Loss mechanisms and high-power piezoelectric components 499

Table 16.3

Piezoelectric properties of semi-hard piezoelectric ceramics based on Pb(Zn

1/3

2/3

–Pb(Ni

1/3

2/3

–Pb(Zr

0.5

sinterable at 900 °C.

Composition Sintering

εε

(°C)

(m/s)

condition (planar) (31-mode)

HP-HT-6-2 1200/2 h 1951 1815 739 239 0.56 0.3 285.6 0.6

HP-HT-12-4 1200/2 h 1502 1404 1653 330 0.573 0.33 289.58 0.58

HP-LT-17-3 900/2 h 1282 * 1326 294 0.56 * * 0.41

On measuring.

HP-HT-6-2: Pb(Zr,Ti)-Pb(Zn,Ni)Nb with Sb, Li and Mn substitution.

HP-HT-12-4: Further modification on the HP-HT-6-2.

HP-LT-17-3: Low temperature sintering of the HP-HT-12-4 with CuO and Bi

WPNL2204