Zuo-Guang. Ye Advanced Dielectric Piezoelectric and Ferroelectric Materials: Synthesis, Characterisation and Applications

Подождите немного. Документ загружается.

Handbook of dielectric, piezoelectric and ferroelectric materials540

WPNL2204

541

18.1 Introduction

The principal thrust of ferroelectric thin-film research and development has

been to the production of non-volatile random access memories (FRAMs);

in contrast to ‘volatile’ dynamic RAMs (DRAMs), such non-volatile devices

retain stored memory in the event of a power failure. Although DRAMs are

volatile, they are unlikely to disappear in the foreseeable future, because

they combine high density (Gbits), high speed and low cost. Nevertheless, in

applications where volatility would require heavy, power-consuming and

cumbersome hard-disk back-up memory (banking, aerospace, or mobile

telephones and digital cameras), the new ferroelectric FRAMs compete

primarily with ‘Flash’/EEPROM devices (electrically erasable read-only

memories). The long-term advantages of FRAMs over EEPROMs are in part

due to the lowering of standard silicon logic levels from the present 5.0 volt

standard to 3.3V, 1.1V and eventually 0.5V. FRAMs can already meet these

lower voltage requirements, whereas it will be physically difficult for Flash

devices to do so, perhaps necessitating cumbersome and unreliable ‘charge

pumps’ to provide 5V internally from a 1.0V external source. The next

application of FRAMs is likely to be memories in digital cameras, and the

size (see below) is now nearly sufficient for use as the audio memory in

stereo devices such as the Sony Walkman. FRAMs are already in use for

‘smart’ credit cards and for video games (a 32 kb FRAM from Fujitsu is

already in every Sony Playstation 2).

Despite the attention focused on FRAMs, memories are not the only

trendy development in ferroelectric thin-film devices (Clark and Lagerwall

1980; Lagerwall 2004), and below I review a dozen other major trends and

areas of R&D, based in part upon my recent reviews of the field in Science

and the Journal of Physics Condensed Matter (Scott, 2006ab).

Recent prototype applications and milestones include ultra-fast (280 ps)

switching (Li et al., 2004), cheap room-temperature magnetic field detectors

to replace SQUIDs (superconducting quantum interference devices),

Ferroelectric nanostructures for

device applications

J F SCOTT, Cambridge University, UK

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials542

piezoelectric nanotubes for microfluidic systems, electrocaloric coolers for

computers, phased-array radar and three-dimensional trenched capacitors

for DRAMs. Tera-bit/square-inch ferroelectric arrays of lead zirconate–titanate

have been reported on Pt nanowire interconnects, and nano-rings with 5–10

nm diameters. Finally, electron emission from ferroelectrics is a relatively

unexploited phenomenon that already yields prototypes of cheap, very small,

high-power microwave devices, as well as miniature X-ray and neutron

sources (‘cold fusion’).

18.2 Ferroelectric nanostructures

The prefix ‘nano-’ is generally defined as <0.1 micrometres, and although

ferroelectric capacitors and related devices are now submicrometre, they are

400–500nm on a side, not 100, with thickness ca. 50–150nm (Fig. 18.1). As

the sizes of ferroelectric cells continue to shrink to true nano-scale, two

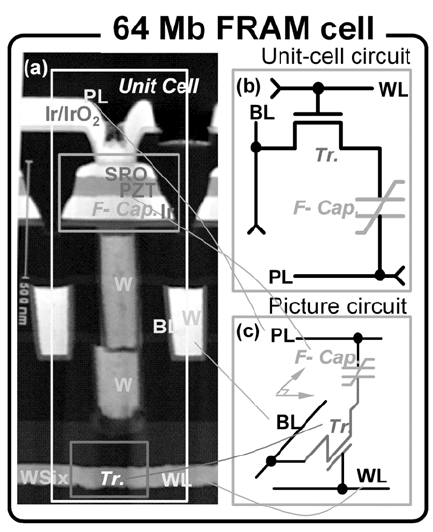
18.1

(a) TEM cross-section for state-of-the-art FRAM: a 64 Mb PZT

device with cell size approximately 400 × 450 × 144 nm

. (b) and (c)

illustrate the relationship of each component in the TEM micrograph

to the equivalent circuit diagram. The symbols on the left side are: Ir

– iridium; SR – SrRuO

; W – tungsten; and Tr. – transistor. On the

right side: WL – word-line; BL – bit-line; PL – plate; Tr. – transistor;

and F – ferroelectric thin film.” (Samsung; used by permission).

WPNL2204

Ferroelectric nanostructures for device applications 543

physics questions are important for nano-ferroelectrics: first, are there physical

phenomena such as crystallographic phases or domain structures that are

stable at these sizes that are not present in bulk? And second, are the device

properties qualitatively different on the nano-scale? Phenomena one might

examine include ferroelectric quantum dots and confinement energies, direct

electron tunnelling, unusual phases due to substrate interface strain, and the

general properties of semiconducting ferroelectrics. Most textbooks make

the assumption that ferroelectrics are insulators. Although this is a good

approximation for bulk samples (Pulvari and Kuebler, 1958a,b), in thin film

ferroelectric oxides are generally rather good p-type semiconductors, with a

variety of conduction mechanisms, including Poole-Frenkel and Schottky

(Dawber et al., 2003a; Liu and Li 2004; Pintilie and Alem 2005; Pintilie et

al., 2005). Typical oxide ferroelectrics are wide-gap semiconductors with

band gaps E

= 3.5–4.1eV and both electronic and ionic conduction. Most

are p-type as grown (due to unintentional impurities of low valence, e.g. Na

or K for Ba; Fe for Ti or Nb, and oxygen vacancies). Electron and hole

mobilities are low, ca. 0.1–3.0 cm

/Vs; ionic mobilities (e.g. oxygen vacancies),

ca. 10

–12

/Vs; effective masses are very high, typically m* = 5.0–6.7m

Note that the band mass and the tunnelling effective mass need not be identical

in general, but in most cases they are quite close. If the tunnelling is across

> 2nm, the masses should be equal (Conley and Mahan, 1967; Schnupp,

1967). This means that tunnelling processes at ferroelectric thin film junctions

are quite unlikely, contrary to some hypotheses (Kohlstedt et al., 2002;

Contreras et al., 2003a,b,c) and the conclusions by Tagantsev et al. (2002) or

Baniecki et al. (2003) about Fowler–Nordheim tunnelling with m* = ca.

1.0m

are very unlikely. The large effective mass in these materials, ignored

by Tagantsev, Baniecki et al., should make us sceptical about some physical

hypotheses. Lead zirconate–titanate (PZT), strontium bismuth tantalate (SBT)

and bismuth titanate (BiT) remain the device favourites (Scott and Araujo,

1989; Paz de Araujo et al., 1995).

For any switching ferroelectric device we must understand how the domains

and domain kinetics differ from bulk. Kittel’s law was the first breakthrough

in understanding how domain widths scale with thickness. Some 60 years

ago Kittel published a paper (Kittel, 1946) that showed magnetic domains

exhibit 180-degree stripe widths w that are proportional to the square root of

the crystal thickness d:

= a’d 18.1

This expresses a balance between domain wall energy and surface energy

and was extended to ferroelectrics (Mitusui and Furuichi, 1953) and to

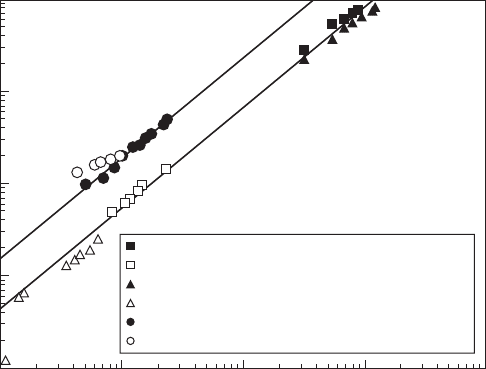
ferroelastics by Roitburd, (1976). It is verified in Fig. 18.2. More recently

Scott (2006a) has shown that this law can be made dimensionless by dividing

by the wall thickness:

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials544

= adδ 18.2

where δ is the domain wall width. In this case, rather remarkably, the equation

applies to all ferroics (ferromagnets, ferroelectrics and ferroelastics) with the

same coefficient (Catalan and Scott 2006):

a = [2π

/21ζ(3)] [χ(a)/χ(c)]

1/2

= 2.455 [χ(a)/χ(c)]

1/2

18.3

where χ(x) are the susceptibilities and ζ(3) the Riemann zeta function of

power 3.

In addition to understanding the static configurations of nano-domains,

we need to understand how their switching depends upon size. That brings

us to the 1962 Kay–Dunn law, which consists of an equally simple law for

the coercive field (minimum switching field E): E

= bd

–2/3

and coercive

voltage V

= bd

1/3

Both of these laws hold from macrosopic millimetre thickness d down to

ca. 2nm. Thus, surprisingly, much of the behaviour of nano-ferroeoectric

domains can be derived from bulk classical physics. However, the smallest

domains found in BaTiO

– 1.0nm – as well as three-dimensional nano-

domains – both violate the Kittel law, and recently Catalan has provided a

multi-dimensional extension of Kittel’s one-dimensional law that clarifies

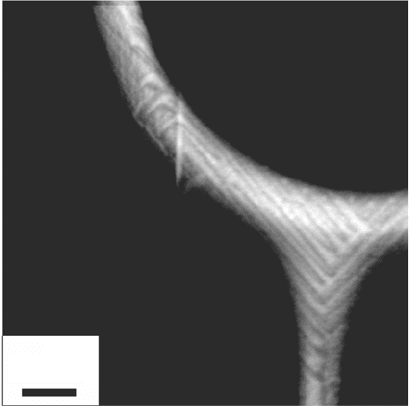
this. Domains are usually studied in flat planes, but some [3D] nanodomains

are shown in Fig. 18.3. Another qualitative difference is that domain switching

in ferroelectrics of submicrometre lateral widths is much more determined

Schilling’s data on BaTiO

Streiffer’s data on PbTiO

Mitsui’s data on Rochelle salt (gradual cooling)

Mitsui’s data on Rochelle salt (sudden cooling)

Dumas’s data on Co

Sparks’s data on Ni

Thickness

1/2

(nm

1/2

)

18.2

Stripe width

vs. thickness

in PbTiO

, BaTiO

and Rochelle

Salt (Schilling

et al.

2006).

WPNL2204

Ferroelectric nanostructures for device applications 545

(rate-limited) by nucleation than by domain wall velocities, so that the early

theory of Pulvari and Kuebler (1958a,b), which included nucleation, works

better than does that of Landauer et al. (1956), as shown recently for Samsung

0.18µm

area PZT cells (Jung et al., 2005). Landauer et al. did not ignore

nucleation; actually they considered it and rejected it, because it would

imply an inductive (phase-lag) part of the switching response, and they

found none in their early experiments. Switching as fast as 280ps has been

demonstrated recently in thin PZT films (Li et al., 2004); however, this is for

small-area capacitors with very small load resistance and a very large driving

source – for real devices with 5V sources and a 10–100ohm load, 60ns is a

more realistic design access time (RC-limited).

Figures 18.4 and 18.5 illustrate nanostructures in thin ceramic films: Fig.

18.4 shows nanotubes; Fig. 18.5, 0.3 Tbit/in

nano-array of Pt-nanowires/

PZT. A rather interesting development in 2005-6 has been the attachment of

nano-capacitors onto the ends of a registered array of carbon nanotubes. This

was first done by Jang et al. (2005), using Si

as the dielectric for the

capacitor; more recently Kawasaki et al. (2007) in our Cambridge lab have

achieved this with a ferroelectric PZT capacitor rather than the non-switching

silicon nitride. In Figs 18.6 and 18.7 other non-planar complex nano-device

structures are shown: Fig. 18.6 is an SEM cross-section of a PZT/CFO

(cobaltous ferrite) magneto-electric composite (Ramesh, Berkeley); Fig. 18.7

shows atomic force microscopy (AFM) nano-writing (Paruch et al., 2006).

Tera-bit ferroelectric memories are not yet a reality: The state of the art

for hard-wired devices is a 0.3Tbit/in

PZT array on Pt-nanowires encased

200 nm

18.3

[3D] nano-domains in BaTiO

(Saad

et al

., 2006).

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials546

in meso-porous Al

(Evans et al., 2007). (An AFM-system 1Tbit/in

single-

crystal device was shown earlier by Cho et al., 2002). Such a 30nm diameter

capacitor still switches 1000–2000 electrons per bit, which is readable at

room temperature (and a good rule of thumb for minimum charge for sense

amplifier error-free detection – single-electron devices are definitely not

realistic in this context), but the registration shown in Fig. 18.4 is not sufficiently

1 µm

18.4

SrBi

nanotubes (Morrison

et al

)2003).

Pt nanowires

BaTiO

Lower

electrode

0.2 µm

18.5

0.5 Tbit/in

nano-array of Pt-nanowires/PZT (Evans

et al

., 2007).

WPNL2204

Ferroelectric nanostructures for device applications 547

long range to make a commercial device, and the prototype wiring has no

individual bit-line interconnects. The problem of registration in mesoporous

alumina has been partially solved by Masuda and Fukuda (1995), who obtained

perfect registration over lengths >> 1µm. Figures 18.5–18.8 illustrate nano-

ferroelectrics fabricated as composites (Fig. 18.5) and from AFM writing

(Fig. 18.6), and via a focused ion beam (FIB) (Figs 18.7, 18.8). The Belfast

group has fabricated complicated [3D] nano-structures, including free-standing

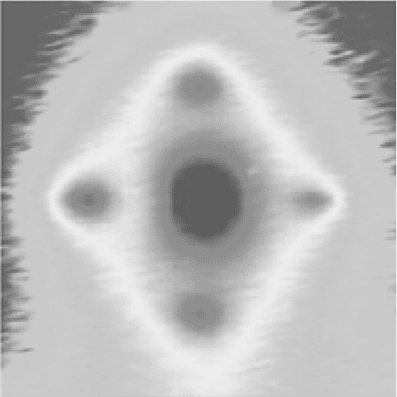
micro-rings from FIB (Fig. 18.8), and a 5 nm inside-diameter PZT nano-ring

(Fig. 18.9) within a pore of mesoporous Si done by chemical solution

deposition. It is important that on the nano-scale these devices can still be

20 nm

PFM

signal

(a.u.)

225 nm

17.7 Gbit/cm

18.6

Magneto-electric composite of CoFe

pillars in a BaTiO

matrix (Zheng

et al

., 2006).

18.7

AFM nano-writing on PZT (Paroch

et al

., 2001).

WPNL2204

Handbook of dielectric, piezoelectric and ferroelectric materials548

switched electrically or used for optical storage (Cho et al., 2002). Using

synchrotron sources (Fig. 18.10) one can study the structure of such very

thin films as functions of temperature and thickness. The 2004 32-Mb FRAM

from Samsung (PZT) or Matsushita (SBT) are still ahead of the commercial

MRAM development (4Mb MRAM from Freescale Co., July 2006), and

2 µm

18.8

Nano-toroid of single-crystal BaTiO

(Saad

et al

., 2006).

EDX line scan

10 nm

18.9

Ultra-nano-toroid of PZT inside a meso-porous Al

pore (Zhu

et al

., 2006 (EDX = energy dispersive X-ray analysis.).

WPNL2204

Ferroelectric nanostructures for device applications 549

Samsung has now (July 2006) a 64Mb FRAM. The ferroelectric-gate field

effect transistor (FET) offers non-destructive read operation, but short retention

times (maximum of a few days – Ishiwara et al., 2004) have thus far precluded

commercial products. A detailed comparison of MRAMs and FRAMs is

given by the author (Scott, 2007), including complex 4T-6C circuits in which

four transistors and six capacitors store each bit. Although the latter circuitry

prevents high-density RAMs, it permits non-destructive read-out.

18.3 Self-patterning

The two basic ways of fabricating nano-ferroelectric devices are, to use

industry jargon, ‘top-down’ – meaning submicrometre lithography – and

‘bottom-up’ – meaning self-assembly. The development of meso-porous silicon

and alumina (and GaN and GaAs) has presented experimentalists with templates

for the latter, and other techniques for coating nano-wires (Sebald et al.,

2005; Fan et al., 2006) have developed independently. Self-assembly of

nano-electrodes on ferroelectric films was first reported by Alexe et al.

(1998) and in PZT nano-arrays, data and a model were published by Dawber,

et al. (2003b) (Fig. 18.11) based upon the original theory (Andreev, 1981)

that such islands would repel each other through their mutual strain interactions

with the substrate. Although self-assembly often results in arrays that have

only short-range order, complete registration satisfactory for commercial

RAM memory devices was achieved by Ma and Hesse (2004) via deposition

with inert spacers, such as mono-disperse submicrometre or micrometre-

18.10

In-plane diffuse X-ray scattering profiles around the PbTiO

<303> Bragg peak at 549 K (Auciello, 2006).

WPNL2204