Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


L AB V ISIT 7
1988 study done in a Louisiana forest, finding A. triseriatus and A. albopictus as
the two dominant species, at 81% and 17% of larvae collected, respectively.
Since the completion of this project, the authors of the study have begun to
search for the mechanism behind this pronounced difference in the habitats. For
example, it is not yet known whether there is a biochemical difference between
treehole water and tire water that can account for the differing results. In any
case, the experiment suggests that the tiger mosquito has a distinct competitive
advantage in the man-made environment of automobile tires.
327

C HAPTER E IGHT
Periodic Orbi ts and
Limit Sets
T
HE BEGINNING of this book was devoted to an understanding of the asymptotic
behavior of orbits of maps. Here we begin a similar study for solution orbits of
differential equations. Chapter 7 contains examples of solutions that converge to
equilibria and solutions that converge to periodic orbits called limit cycles. We
will find that the dimension and shape of the phase space put serious constraints
on the possible forms that asymptotic behavior can take.
For autonomous differential equations on the real line, we will see that
solutions that are bounded must converge to an equilibrium. For autonomous
differential equations in the plane, a new limiting behavior is possible—solutions
that are bounded may instead converge to closed curves, called periodic orbits or
cycles. However, nothing more radical can happen for solutions of autonomous
differential equations in the plane. Solutions cannot be chaotic. The topological
329
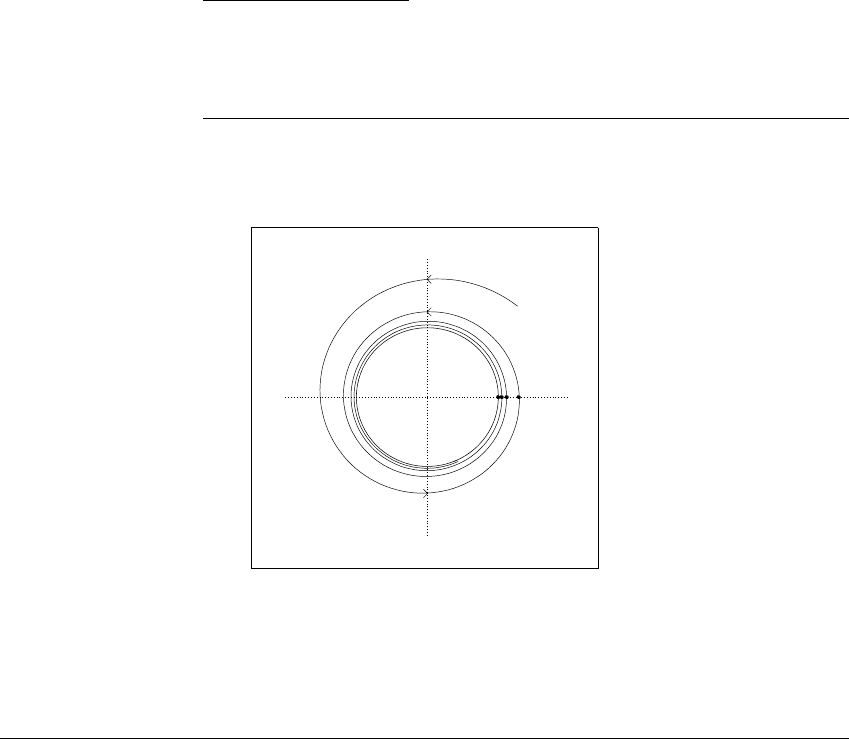
P ERIODIC ORBITS AND L IMIT S ETS
rule about plane geometry that enforces this fact is the Jordan Curve Theorem.
Winding solutions can wind only in a single direction, as shown in Figure 8.7.
This is the subject of the Poincar
´
e-Bendixson Theorem, which is one of the
main topics of this chapter. In three-dimensional space, there is no such rule.
The one extra dimension makes a difference. We will investigate several chaotic
three-dimensional equations in Chapter 9.
Typical limiting behavior for planar systems can be seen in the equation
˙
r ⫽ r(1 ⫺ r)
˙
⫽ 8, (8.1)
where r and
are polar coordinates. There is an equilibrium at the origin r ⫽ 0
and a periodic orbit circling at r ⫽ 1.
✎ E XERCISE T8.1
Show that all nonequilibrium solutions of (8.1) have form (r,
) ⫽
(ce
t
(ce
t
⫺ 1), 8t ⫹ d) for some constants c, d.
The solution of (8.1) with initial condition (r,
) ⫽ (2, 0) is shown in
Figure 8.1. It spirals in forever toward the periodic solution r ⫽ 1, also shown.
p
Figure 8.1 The definition of an
-limit set.
The point p is in the
-limit set of the spiraling trajectory because there are points
F(t
1
, v
0
), F(t
2
, v
0
), F(t
3
, v
0
) ... of the trajectory, indicated by dots, that converge
to p. The same argument can be made for any point in the entire limiting circle of
the spiral solution, so the circle is the
-limit set.
330

8.1 LIMIT S ETS FOR P LANAR D IFFERENTIAL E QUATIONS
For this reason, we will say that the periodic solution r ⫽ 1 is the limit set of the
spiraling solution. We will usually use the terminology
-limit set, to emphasize
that we are interested in final, or asymptotic, behavior. In Section 8.1 we define
limit set and give examples in one and two dimensions.
8.1 LIMIT SETS FOR PLANAR
DIFFERENTIAL EQUATIONS
We begin with an autonomous differential equation
˙v ⫽ f(v), (8.2)
where f is a map of ⺢
n
, which is differentiable or at least Lipschitz, to guaran-
tee uniqueness. Throughout this chapter all differential equations will be au-
tonomous; the function f of (8.2) does not depend explicitly on t. For v 僆 ⺢
that means f is a scalar (one-dimensional) map. When v is a vector in ⺢
2
, f is a
vector-valued function of two scalar variables, and the phase portrait of (8.2) is a
phase plane.
Recall the definition of flow in Chapter 7. For a point v
0
in ⺢
n
,wewrite
F(t, v
0
) for the unique solution of (8.2) satisfying F(0, v
0
) ⫽ v
0
.
Definition 8.1 A point z in ⺢
n
is in the
-limit set
(v
0
) of the solution
curve F(t, v
0
) if there is a sequence of points increasingly far out along the orbit
(that is, t → ⫹
⬁
) which converges to z. Specifically, z is in
(v
0
) if there exists an
unbounded increasing sequence 兵t
n
其 of real numbers with lim
n→
⬁
F(t
n
, v
0
) ⫽ z.
A point z is in the
␣
-limit set
␣
(v
0
) if there exists an unbounded decreasing
sequence 兵t
n
其 of real numbers (t
n
→ ⫺
⬁
) with lim
n→
⬁
F(t
n
, v
0
) ⫽ z.
The concept of
-limit set (or forward limit set) first appeared for maps in
Chapter 6. For maps, the unbounded, increasing sequence 兵t
n
其 of real numbers in
Definition 8.1 is replaced by an (unbounded) increasing sequence 兵m
n
其 of positive
integers (iterates of the map).
If v
0
is an equilibrium, then
(v
0
) ⫽
␣
(v
0
) ⫽ 兵v
0
其. Furthermore, for any
v
0
the
␣
-limit set of the equation ˙v ⫽ f(v)isthe
-limit set of ˙v ⫽⫺f(v). See
Exercise 8.13.
E XAMPLE 8.2
Recall the one-dimensional example
˙
x ⫽ x(a ⫺ x)
331
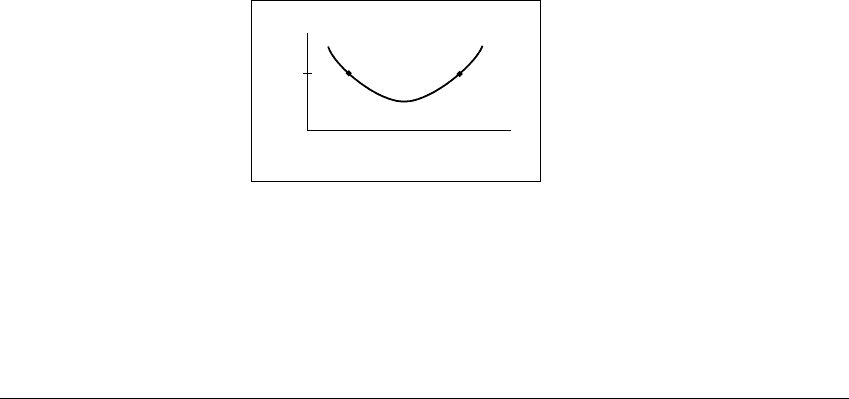
P ERIODIC ORBITS AND L IMIT S ETS
from Chapter 7. Assume that a ⬎ 0. There are two equilibria in ⺢, x ⫽ 0andx ⫽ a.
All trajectories with x
0
⬎ 0 converge to the stable equilibrium x ⫽ a. According to
the above definition,
(x
0
) ⫽ 兵a其 for x
0
⬎ 0. Since 0 is an equilibrium,
(0) ⫽ 兵0其.
If x
0
⬍ 0, the trajectory diverges to ⫺
⬁
, and therefore
(x
0
) is the empty set.
With this example in mind, it is easy to describe the asymptotic behavior
(the
-limit set) for any bounded orbit of an autonomous differential equation
on the real line.
Theorem 8.3 All solutions of the scalar differential equation
˙
x ⫽ f(x) are
either monotonic increasing or monotonic decreasing as a function of t. For x
0
僆 ⺢,if
the orbit F(t, x
0
),tⱖ 0, is bounded, then
(x
0
) consists solely of an equilibrium.
Figure 8.2 shows a nonmonotonic scalar function x(t), together with an
explanation (in the caption) as to why it cannot be the solution to a scalar
equation
˙
x ⫽ f(x).
Proof of Theorem 8.3: Assume that for a fixed initial condition x
0
,there
is some t
ⴱ
at which the solution F(t, x
0
) has a local maximum or local minimum
x
ⴱ
, as a function of t.Then
˙
x(t
ⴱ
) ⫽ f(x
ⴱ
) ⫽ 0. Hence x
ⴱ
is an equilibrium, and
there is a solution identically equal to x
ⴱ
. By uniqueness of solutions, F(t, x
0
)must
be the equilibrium solution; F(t, x
0
) ⬅ x
ⴱ
, for all t. This means that no solution
can “turn around”. All solutions are monotonic.
x
1
t
x
Figure 8.2 Why nonmonotonic functions cannot be solutions of a scalar au-
tonomous equation.
The function x(t) depicted here cannot be the solution of a scalar equation
˙
x ⫽ f(x).
Notice that the solution passes through the value x
1
twice, once with positive slope
and once with negative slope. The value of f(x
1
) is either positive or negative (or
zero), however, and it must equal the slope at both points. The point x
1
can be
chosen so that f(x
1
) is not 0.
332

8.1 LIMIT S ETS FOR P LANAR D IFFERENTIAL E QUATIONS
On an interval [x
0
,x
1
] not containing an equilibrium (so that f is not zero),
we can rewrite the equation as
dt
dx
⫽
1
f(x)
.
Integrating both sides from x
0
to x
1
yields
t(x
1
) ⫺ t(x
0
) ⫽
x
1
x
0
dx
f(x)
⬍
⬁
.
We conclude that a trajectory traverses any closed, bounded interval without
equilibria in finite time.
If f(x
0
) is greater than 0, the orbit F(t, x
0
) must increase as t increases,
as long as it is below the first equilibrium. It cannot stop at any point below
the equilibrium, because it traverses an interval centered at such a point. It
cannot reach the equilibrium, by uniqueness of solutions. Therefore it converges
monotonically to the equilibrium as t →
⬁
. The same argument can be turned
around to handle the case of f(x
0
) ⬍ 0.
Theorem 8.3 describes the
-limit sets for scalar autonomous differential
equations and shows they are rather simple. Either the orbit diverges to infinity,
or if bounded, converges to a single equilibrium. For differential equations of
dimension two and higher, there is another asymptotic behavior, called a periodic
orbit. Like equilibria, periodic orbits can attract solutions, and therefore be
-limit
sets.
Definition 8.4 If there exists a T ⬎ 0suchthatF(t ⫹ T, v
0
) ⫽ F(t, v
0
)
for all t, and if v
0
is not an equilibrium, then the solution F(t, v
0
) is called a
periodic orbit,orcycle. The smallest such number T is called the period of the
orbit.
A periodic orbit traces out a simple closed curve in ⺢
n
. The term closed
curve refers to a path that begins and ends at the same point. Examples include
circles, triangles, and figure-eights. A simple closed curve is one that does not
cross itself. Hence, a figure-eight is not a simple closed curve. By uniqueness of
solutions, the closed curve of a periodic orbit must be simple. We have already
seen examples of cycles. In Example 7.8, the solution F(t, v
0
) is a circle whose
radius is |v
0
|. Every initial condition lies on a circular periodic orbit of period 2
,
except for the origin, which is an equilibrium.
The pendulum equation of Section 7.5 also has cycles when there is no
friction. These solutions correspond physically to full back-and-forth periodic
333
P ERIODIC ORBITS AND L IMIT S ETS
swings of the pendulum. Figure 7.14 shows orbits encircling equilibria that are
simple closed curves traversed by the system.
E XAMPLE 8.5
Here is a general version of (8.1). Let r and
be polar coordinates in the
plane. For a, b ⬎ 0, consider
˙
r ⫽ r(a ⫺ r)
˙
⫽ b. (8.3)
There is an equilibrium at the origin. Therefore
(0) ⫽ 兵0其. See Figure 8.3. For
every other initial condition (r
0
,
0
) ⫽ 0, the trajectory moves counterclockwise
around the origin and the
-limit set is the circle r ⫽ a. Figure 8.3(a) shows the
phase plane for this system.
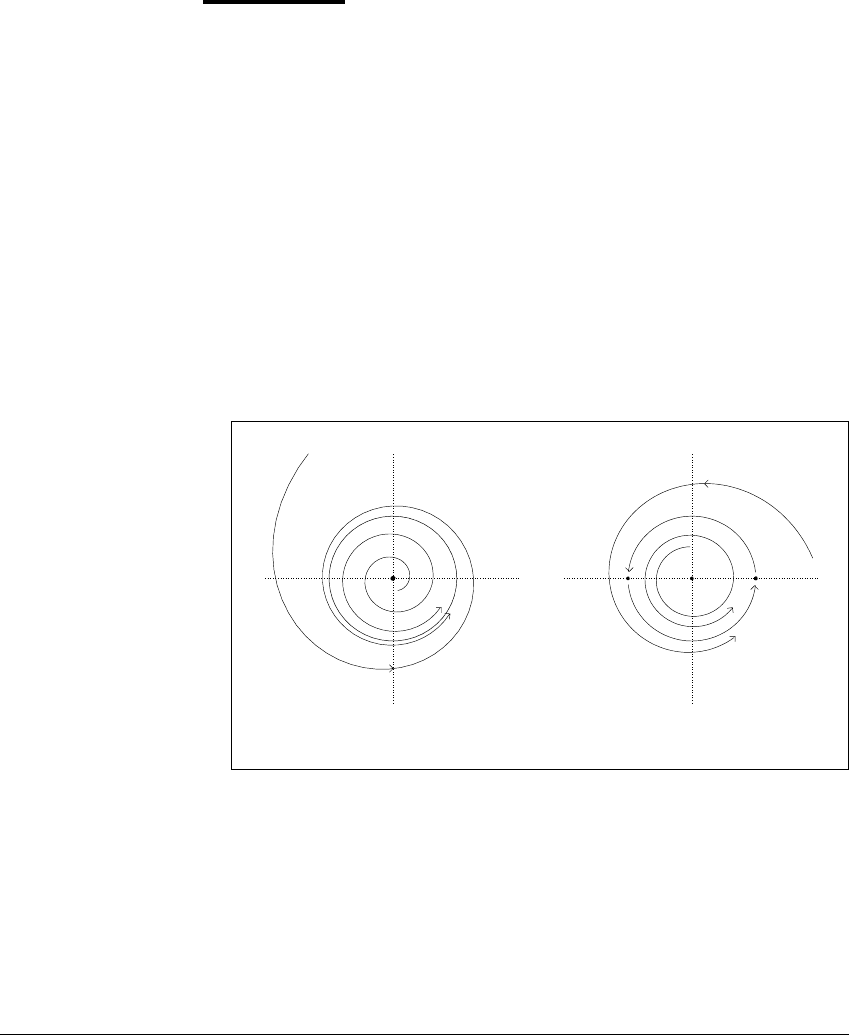
y
x
y
x
(a) (b)
Figure 8.3 Examples of
-limit sets for planar flows.
(a) The phase plane for Example 8.5 shows the circle r ⫽ a as an attracting periodic
orbit of system (8.3). The origin is an unstable equilibrium. The
-limit set of
every trajectory except the equilibrium is the periodic orbit. (b) The phase plane
for Example 8.6 looks very similar to the phase plane in (a), except that in this
example there are no periodic orbits. There are three equilibria: the origin and the
points (a, 0) and (a,
). Every other point on the circle r ⫽ a is on a solution called
a connecting arc, whose
␣
-and
-limit sets are the equilibria. The
-limit set of
each nonequilibrium solution not on the circle is the circle r ⫽ a.
334

8.1 LIMIT S ETS FOR P LANAR D IFFERENTIAL E QUATIONS
✎ E XERCISE T8.2
Solve the differential equation (8.3), and verify the statements made about
-limit sets in Example 8.5.
➮ COMPUTER EXPERIMENT 8.1
Write a computer program to plot numerical solutions of the Van der Pol
equation
¨
x ⫹ (x
2
⫺ 1)
˙
x ⫹ x ⫽ 0. Plot the attracting periodic orbit that was proved
to exist in Challenge 7. Find the
-limit sets for all planar orbits.
E XAMPLE 8.6
Example 8.5 can be modified so that it does not have any periodic orbits. We
can destroy the circular orbit at r ⫽ a by making an adjustment in the equation
for
˙
. For example, replace b in the equation by a function g(r,
)thatisalways
positive except for the two points (r,
) ⫽ (a, 0) and (a,
),whereitiszero.If
we use g(r,
) ⫽ sin
2
⫹ (r ⫺ a)
2
, the equation is
˙
r ⫽ r(a ⫺ r)
˙
⫽ sin
2
⫹ (r ⫺ a)
2
.
This equation is much harder to solve explicitly than (8.3), but we can derive
lots of qualitative information without an explicit formula for the solution. For
any initial condition not on the circle r ⫽ a, the limit set has not changed from
the previous example. Except for the equilibrium trajectory at the origin, these
trajectories limit on the entire circle. The novel aspect of this example is that
trajectories on the circle itself do not have the entire circle as the limit set. Figure
8.3(b) shows the phase plane for this system. On the circle r ⫽ a there are two
equilibria, (a, 0) and (a,
). The trajectory through any other point on the circle
hasasits
␣
-and
-limit sets these equilibria. Nonequilibrium solutions such as
these, whose limit sets contain only equilibria, are called connecting arcs.
E XAMPLE 8.7
The pendulum solutions in Figure 7.14 show two types of
-limit sets.
One type is an equilibrium, which is its own
-limit set and which is also the
335

P ERIODIC ORBITS AND L IMIT S ETS
limit set of the connecting arcs. The connecting arcs are solutions that approach
the equilibria ((2k ⫹ 1)
, 0), (k ⫽⫾1, ⫾2,...), as t → ⫾
⬁
. The other type of
-limit set is a cycle, which is again its own limit set. The pendulum also has
unbounded orbits (which have no limit sets).
We again raise the question: What types of sets in ⺢
2
can be
-limit
sets of a bounded solution of an autonomous differential equation? We have
seen examples of points (equilibria) and closed curves (periodic orbits), and sets
containing equilibria and connecting arcs, as in Example 8.6. Can flows on ⺢
2
have chaotic limit sets? The answer to this question is “no”. We shall see in the
remainder of this chapter that the types of
-limit sets are severely restricted by
intrinsic topological properties of the plane.
➮ COMPUTER EXPERIMENT 8.2
Write a computer program to compute numerical solutions of the double-
well Duffing oscillator
¨
x ⫹ 0.1
˙
x ⫺ x ⫹ x
3
⫽ 0. There are two stable equilibria
corresponding to the bottoms of the wells. Plot the set of initial values in the
(x,
˙
x)-plane whose
-limit set is the equilibrium point (1, 0). How would you
describe the set of points whose
-limit set is the point (0, 0)?
The celebrated Poincar
´
e-Bendixson Theorem, which we state in this sec-
tion and prove in Section 8.3, gives a classification of planar
-limit sets. An
-limit set of a two-dimensional autonomous equation must be one of the fol-
lowing: (1) a set of equilibria; (2) a periodic orbit; or (3) a set containing only
equilibria and connecting arcs. Figure 8.3(b) shows a circle with two connecting
arcs on it. The entire circle is a limit set of the trajectory spiraling in towards it.
This example has
-limit sets of types (1) and (3).
We usually deal with equations whose equilibria are isolated, meaning that
there are only finitely many in any bounded set. In particular, this implies that
each equilibrium has a surrounding neighborhood with no other equilibria. For
such equations, a type (1) limit set contains only one equilibrium point. None
of these three types of
-limit sets can be a chaotic set. In each case, as an orbit
converges to one of these sets, its behavior is completely predictable. In particular,
such a set may contain a dense orbit only if the limit set is either a periodic orbit
or an equilibrium point. Thus we can conclude from the following theorem that
for autonomous differential equations, chaos can occur only in dimension three
336

8.2 PROPERTIES OF
-LIMIT S ETS
and higher. As we have seen, there can be chaos in one-dimensional maps, and
for invertible maps it can occur in dimensions two and higher.
Theorem 8.8 (Poincar
´
e-Bendixson Theorem.) Let f be a smooth vector
field of the plane, for which the equilibria of ˙v ⫽ f(v) are isolated. If the forward orbit
F(t, v
0
),tⱖ 0, is bounded, then either
1.
(v
0
) is an equilibrium, or
2.
(v
0
) is a periodic orbit, or
3. For each u in
(v
0
), the limit sets
␣
(u) and
(u) are equilibria.
The hypothesis that the equilibria are isolated is included to simplify the
statement of the theorem. If this assumption is omitted, then we have to include
the possibility that either
(v
0
)or
(u) is a connected set of equilibria.
The three possibilities allowed by Theorem 8.8 are illustrated in Figure 8.4.
In (a), the
-limit set of the solution shown is an equilbrium; in (b) both solutions
have the circular periodic solution as
-limit set. In (c), the
-limit set of the
outermost orbit is the equilibrium P together with the two connecting arcs that
begin and end at P. As required by Theorem 8.8, any point u in
(v
0
) has the
property that
(u) ⫽ P.
In the next section we discuss properties of limit sets, not just for planar
flows, but for autonomous equations in any dimension. These properties are
then used in the proof of the Poincar
´
e-Bendixson Theorem, which is given in
Section 8.3.
8.2 PROPERTIES OF
-LIMIT SETS
Now that we have seen some common examples of
-limit sets, we turn to a
more theoretical investigation and establish five important properties of all
-
limit sets. The statements and proofs of these properties involve the concept of
“limit point”, a concept we have previously seen, although not explicitly, in all
our discussions of limit sets. Specifically, a point v in ⺢
n
is called a limit point of
asetA if every neighborhood N
⑀
(v) contains points of A distinct from v. This
means that there is a sequence of points in A that converge to v. A limit point
v of A maybeinA or it may not be. A set A that contains all its limit points
is called a closed set. Thus, for example, if a and b are real numbers, then the
intervals [a, b], [0,
⬁
), and (⫺
⬁
,
⬁
) are closed, while the intervals [a, b), (a, b),
and (0,
⬁
) are not. In the plane, the unit disk (with its boundary circle) is a closed
set, while the interior of the disk, all points (x, y)suchthatx
2
⫹ y
2
⬍ 1, is not
337
