Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.

P ERIODIC ORBITS AND L IMIT S ETS
y
x
y
x
(a) (b)
P
(c)
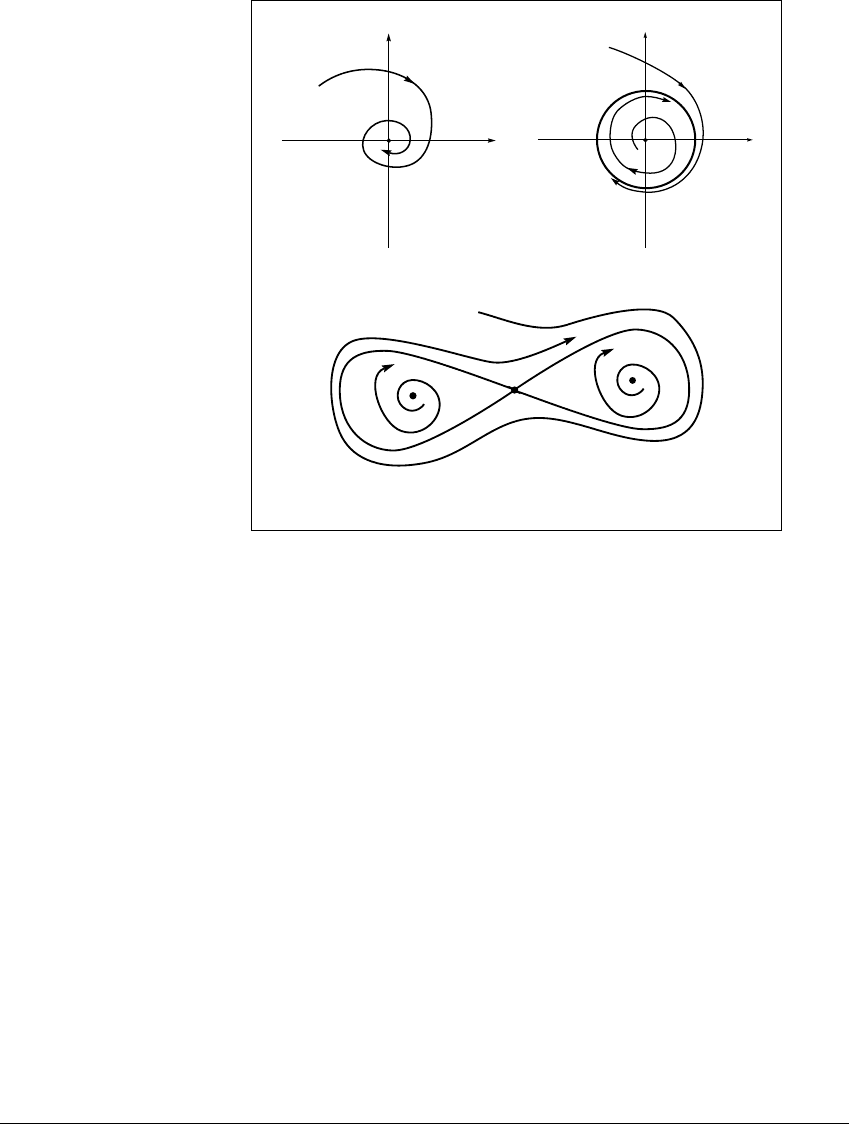
Figure 8.4 Planar limit sets.
The three pictures illustrate the three cases of the Poincar
´
e-Bendixson Theorem.
(a) The limit set is one point, the origin. (b) The limit set of each spiraling trajectory
is a circle, which is a periodic orbit. (c) The limit set of the outermost trajectory is
a figure eight. This limit set must have an equilibrium point
P at the vertex of the
“eight”. It consists of two connecting arcs plus the equilibrium. Trajectories on the
connecting arcs tend to
P as t →
⬁
and as t
→ ⫺
⬁
.
closed. (Take away any point on the boundary circle x
2
⫹ y
2
⫽ 1 and the set will
not be closed.)
An important fact about limit points is that any set that is both infinite and
bounded will have limit points. This fact is called the Bolzano-Weierstrass The-
orem, and it can be found in any standard advanced calculus text—for example,
(Fitzpatrick, 1996).
Now we can proceed with the properties of
-limit sets. Let ˙v ⫽ f(v), v 僆
⺢
n
, be an autonomous differential equation, and let
(v
0
)bethe
-limit set of
an orbit F(t, v
0
).
• Existence Property. If the orbit F(t, v
0
) is bounded for all t ⱖ 0, then
(v
0
)
is non-empty.
338

8.2 PROPERTIES OF
-LIMIT S ETS
Proof: The sequence 兵F(n, v
0
):n ⫽ 1, 2, 3,...其 either is a bounded infi-
nite set (which must have a limit point) or repeats the same point infinitely many
times. In either case, a point is in
(v
0
).
• Property of Closure.
(v
0
)isclosed;thatis,
(v
0
) contains all of its limit
points.
✎ E XERCISE T8.3
Prove the Property of Closure.
In order to prove the next property, we will have to reparametrize orbits.
Since the solution of an autonomous equation goes through a point independent
of the time that it reaches the point, we could solve an equation up to time t
in different ways: either directly find F(t, v
0
), or write t as t
1
⫹ t
2
and solve by
first finding F(t
1
, v
0
), then using v
1
⫽ F(t
1
, v
0
) as our new initial point, find
F(t
2
, v
1
). In other words, we can stop and start the process, reparametrizing
along the way, and still end up with the same solution. In mathematical terms,
F(t
1
⫹ t
2
, v
0
) ⫽ F(t
2
, F(t
1
, v
0
)). We refer to this equivalence as the composition
property (also called the semi-group property) of autonomous equations.
• Property of Invariance.
(v
0
) is invariant under the flow; that is, if u is in
(v
0
), then the entire orbit F(t, u)isin
(v
0
).
✎ E XERCISE T8.4
Prove the Property of Invariance.
The next property involves the topological concept called connectedness.
Loosely speaking, a set is “connected” if it is geometrically of one piece. For a
closed set (one that contains all its limit points) that is also bounded, we have the
following characterization: a closed, bounded set S is called connected if it is not
possible to write S ⫽ A 傼 B, where the sets A and B are a positive distance apart.
More precisely, there are no sets A and B such that S ⫽ A 傼 B and there is a
distance d ⬎ 0 with each point of A separated from each point of B by a distance
of at least d.
• Property of Connectedness. If 兵F(t, v
0
)其 is a bounded set, then
(v
0
)is
connected.
339

P ERIODIC ORBITS AND L IMIT S ETS
Proof: Suppose
(v
0
) ⫽ A 傼 B, where sets A and B are d apart. There
are infinitely many disjoint segments of solution curves moving from within d 4
of A to within d 4ofB.SinceA and B are separated by d, there must be a point
on each such segment that is d 2fromA. Such points are at least d 2fromB.
These points form a bounded infinite set that has a limit point lying at least d 2
from
(v
0
). Therefore, d must be 0.
• Property of Transitivity. If z 僆
(u)andu 僆
(v
0
), then z 僆
(v
0
).
✎ E XERCISE T8.5
Prove the Property of Transitivity.
The same five properties hold for
␣
-limit sets since, as mentioned previously,
every
␣
-limit set of the equation ˙v ⫽ f(v)isan
-limit set of ˙v ⫽⫺f(v). (Exercise
8.13.) We summarize the properties of
-limit sets in a table for easy reference.
Properties of
-limit sets
1. Existence: The
-limit set of a bounded orbit is non-empty.
2. Closure: An
-limit set is closed.
3. Invariance: If y is in
(v
0
), then the entire orbit F(t, y)isin
(v
0
).
4. Connectedness: The
-limit set of a bounded orbit is connected.
5. Transitivity: If z is in
(y)andy is in
(v
0
), then z is in
(v
0
).
We return now to the subject of Lyapunov functions (introduced in Chapter
7) to determine the behavior of these functions on limit sets. Recall that for a
Lyapunov function E : ⺢
n
→ ⺢, the value of E along an orbit decreases with
time:
dE
dt
(F(t, v)) ⱕ 0. The following lemma says that the value of E is constant
on limit sets. For any positive real number c, we let
W
c
⫽ 兵v 僆 ⺢
n
: E(v) ⱕ c其.
In Exercise T7.16 it was shown that, for each c, W
c
is a forward invariant set.
Lemma 8.9 Let v
0
僆 W
c
, for some c ⬎ 0. Then there is a number
d, 0 ⱕ d ⱕ c, such that E(v) ⫽ d, for every v 僆
(v
0
).
340

8.3 PROOF OF THE P OINCAR
´
E -BENDIXSON T HEOREM
Since E is constant on
(v
0
)and
(v
0
) is an invariant set, we have the
following corollary.
Corollary 8.10
˙
E(v) ⫽ 0 for each v in
(v
0
).
✎ E XERCISE T8.6
Prove Lemma 8.9.
Lyapunov functions provide a method of showing that an equilibrium is
asymptotically stable and measuring the extent of the basin of attraction for such
an equilibrium. We use Lemma 8.9 to prove LaSalle’s Corollary (Corollary 7.26).
Let E be a Lyapunov function for
v, let W be a neighborhood of v as in
the hypothesis of Corollary 7.26. Let Q ⫽ 兵v 僆 W :
˙
E(v) ⫽ 0其. Assume that
v is an isolated equilibrium and that W is forward invariant. We prove that
if the only forward invariant set contained completely in Q is
v, then v is
asymptotically stable. Furthermore, W is contained in the basin of
v; for each
v
0
僆 W, lim
t→
⬁
F(t, v
0
) ⫽ v.
Proof of Corollary 7.26 (LaSalle’s Corollary): Since E is constant on
(v
0
), the limit set
(v
0
) is contained in Q. Also,
(v
0
) is forward invariant.
Therefore,
(v
0
) ⫽ v.
8.3 PROOF OF THE POINCAR
´
E -BENDIXSON
THEOREM
The proof of the Poincar
´
e-Bendixson Theorem is illuminating. We will break
down the ideas into a series of lemmas. In the first lemma below, we develop a
picture of the flow in a small neighborhood of a nonequilibrium point u. In such
a neighborhood, solution curves run roughly parallel to the orbit through u.
For a nonequilibrium point u, let L be a short line segment containing u
but no equilibrium points, which is both perpendicular to the vector f(u)and
short enough so that for each v in L, the vector f(v) is not tangent to L. We call
such a segment a transversal at u.
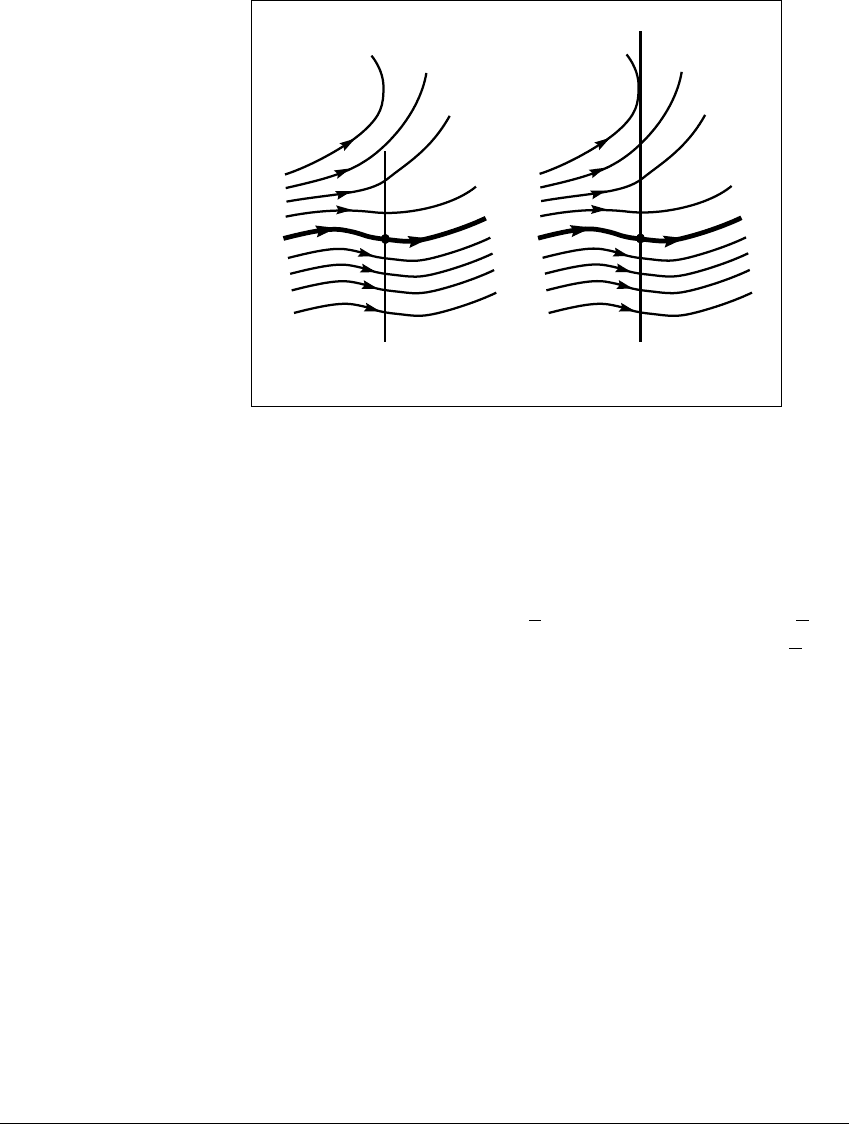
In Figure 8.5, L is a transversal at u, but L
ⴱ
is not a transversal at u. Notice,
in particular, that all solution curves that intersect the transversal cross from the
same side as the orbit through u. If instead some solutions crossed from left to
341
P ERIODIC ORBITS AND L IMIT S ETS
u
L
L
*
u
(a) (b)
Figure 8.5 Illustration of a transversal line segment at a non-equilibrium
point.
(a) A transversal line segment L through a non-equilibrium point u is shown.
(b) The segment L
ⴱ
is not a transversal because it is tangent to the vector field at a
point on the top solution curve shown.
right and others from right to left, then
dx
dt
⬎ 0 at some points on L, and
dx
dt
⬍ 0
at other points on L. Then there must be at least one point on L where
dx
dt
⫽ 0,
implying the existence of a tangency or equilibrium.
It is convenient to look now at neighborhoods around u that are diamond-
shaped, rather than round. We define a
␦
-diamond about u, denoted D
␦
(u), to
be the set of points in a square centered at u whose diagonals are of length 2
␦
and
lie, respectively, on the transversal L and on a line segment perpendicular to L
(that is, it is parallel to the vector f(u)). A
␦
-diamond is illustrated in Figure 8.6.
The following lemma states that the solution through each initial point
in a sufficiently small
␦
-diamond about u must cross a transversal at u in either
forward or backward time before leaving the diamond. To simplify notation, let
v(t) denote the orbit F(t, v
0
). In the proof of the following lemma, we let f
1
and f
2
be the coordinate functions of the vector function f of (8.2); f(v) ⫽ (f
1
(v),f
2
(v)).
Sets of the form S ⫽ 兵F(t, v
0
):t
1
ⱕ t ⱕ t
2
其 (for some v
0
僆 ⺢
2
and real numbers
t
1
and t
2
) are called trajectory segments (or orbit segments).
Lemma 8.11 (The Diamond Construction.) Let L be a transversal at u.
For
␦
⬎ 0 sufficiently small there exists a
␦
-diamond D
␦
(u) about u such that if
342
8.3 PROOF OF THE P OINCAR
´
E -BENDIXSON T HEOREM
L
v
0
u
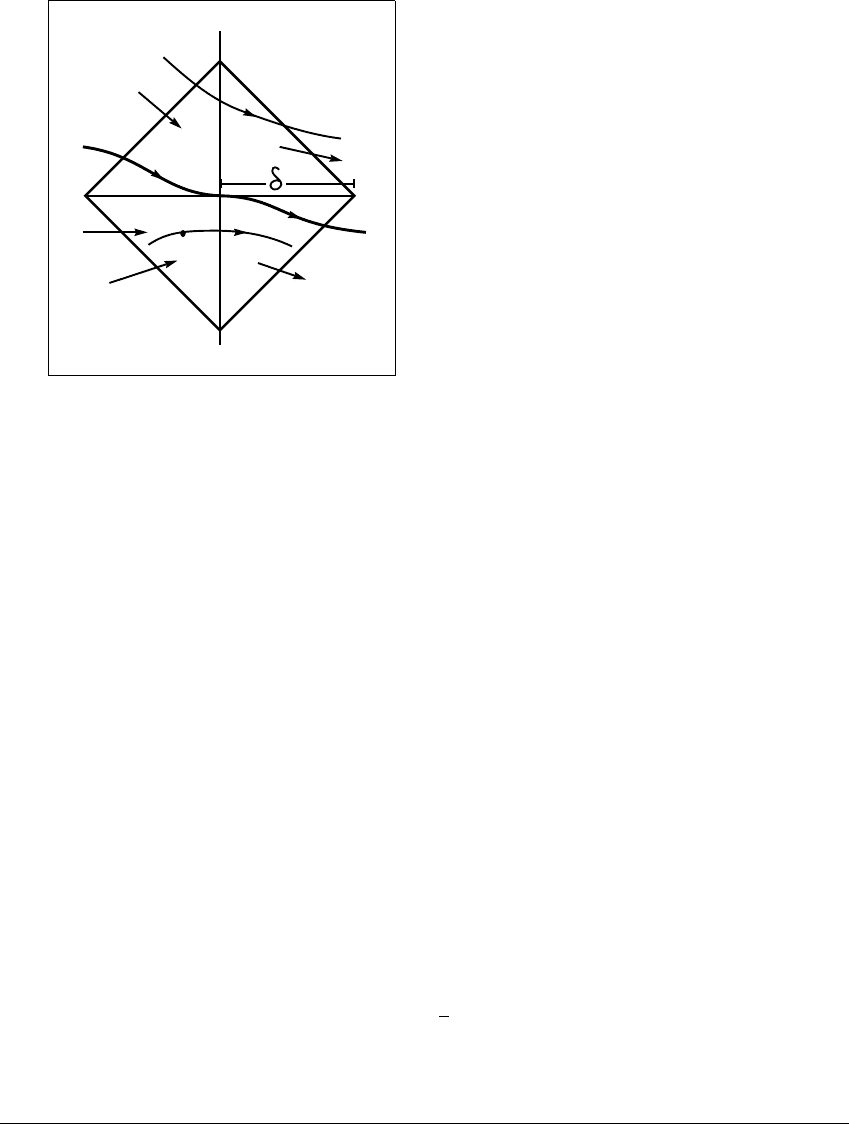
Figure 8.6 Illustration of a
␦
-diamond.
A
␦
-diamond is a square neighborhood of a nonequilibrium point u. Its diagonals
are of length 2
␦
, and which lie on the transversal L and on the line segment in
the direction of f(u). The Diamond Construction guarantees that there is a
␦
-
diamond such that for each v
0
in the interior of the diamond there is an orbit
segment completely contained in the diamond that passes through v
0
with positive
horizontal speed and intersects L.
v
0
is in the interior of D
␦
(u), then there is a trajectory segment that contains v
0
,
is completely contained in D
␦
(u), and intersects L.
Proof: We choose coordinates (x, y)sothatu ⫽ (0, 0) and f(u) ⫽ (a, 0),
for some a ⬎ 0. Then L is on the y-axis. Choose
␦
⬎ 0 sufficiently small so that
for z in D
␦
(u) the following conditions hold:
1. The slope of f(z) (that is, f
2
(z) f
1
(z)) is strictly between ⫺1 and 1. This
restriction is possible since the slope is 0 at u.
2. f
1
(z) ⬎ a 2.
Notice, in particular, that the slope is between ⫺1 and 1 on the edges of the
D
␦
(u). A solution can only exit the diamond in forward time through the right-
hand side of the diamond. Similarly, it can only exit the diamond in backward
time through the left-hand side. Now
x(t) ⫺ x(0) ⫽
t
0
f
1
(x(s)) ds ⬎
a
2
t.
Since the maximum value of x(t) ⫺ x(0) is 2
␦
, the solution through an initial
condition v
0
in the diamond must exit the right side of the diamond within time
343
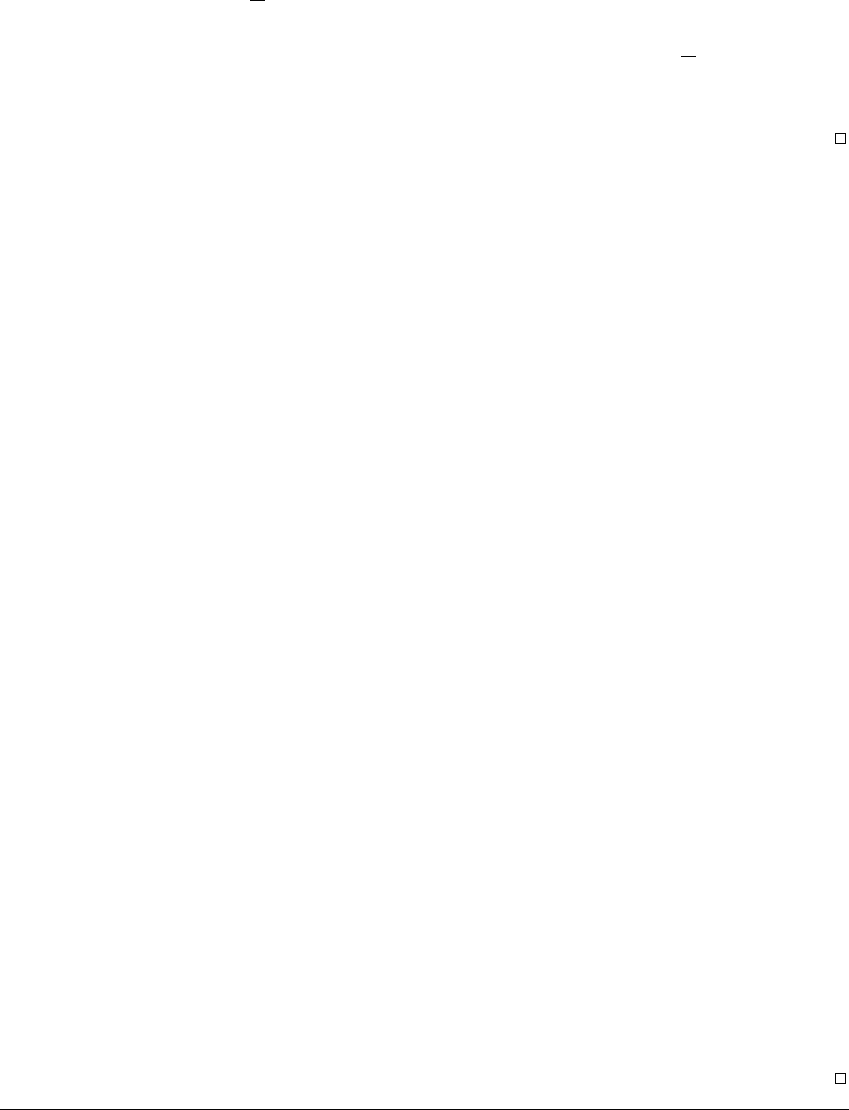
P ERIODIC ORBITS AND L IMIT S ETS
t ⬍ 2
2
␦
a
. Let t
2
be the smallest t value with t ⬎ 0 for which the orbit through
v
0
intersects the right side of D
␦
(u). Similarly, the backward solution (for t
decreasing from 0) must exit the left side within time t, ⫺2
2
␦
a
⬍ t ⬍ 0. Let t
1
be
the largest value of t with t ⬍ 0 for which v(t) intersects the left side of D
␦
(u).
Then the trajectory segment S ⫽ 兵v(t):t
1
ⱕ t ⱕ t
2
其 is contained in D
␦
(u)and
intersects L.
The proof of the Poincar
´
e-Bendixson Theorem depends on the next four
lemmas. These results are strictly for planar flows and, unlike the previous lemma,
have no natural analogue in higher dimensions. First we show that if one trajectory
repeatedly crosses a transversal L, then the crossings must occur in order along
L for increasing t. We will make use of the Jordan Curve Theorem from plane
topology (see, e.g., (Guillemin and Pollack, 1974)). Recall that a simple closed
curve is a path which begins and ends at the same point and does not cross itself.
This theorem says that a simple closed curve divides the plane into two parts: a
bounded region (the “inside”) and an unbounded region (the “outside”). In order
for a path to get from a point inside the curve to a point outside the curve, it must
cross the curve.
Lemma 8.12 (The “In the Bag” or Monotonicity Lemma.) Given t
1
⬍
t
2
⬍ t
3
for which v(t
1
), v(t
2
), and v(t
3
) are three distinct points on L. Then v(t
2
)
is between v(t
1
)andv(t
3
).
Proof: Let L be a transversal at u. Since the orbit v(t) crosses L only
finitely many times between t
1
and t
3
(see Exercise 8.18), it suffices to prove
the conclusion in the case that t
1
⬍ t
2
⬍ t
3
are consecutive times for which
v(t) crosses L.LetC
be the orbit segment of v(t) between v(t
1
)andv(t
2
),
C
⫽ 兵v(t),t
1
ⱕ t ⱕ t
2
其, and let L
be the segment of L connecting these points.
See Figure 8.7. Let C be the closed curve C
傼 L
.NotethatC is simple by the
uniqueness of solutions.
From the Jordan Curve Theorem, there are two cases. In case 1, the vector
field on L
points into the bounded region, and in case 2, it points into the
unbounded region. Figure 8.7 shows case 1. We will assume case 1 holds and leave
to the reader any adjustments that are needed for case 2. Now, the orbit v(t)is
trapped inside C for t ⬎ t
2
, (beyond v(t
2
)). It cannot cross C
by uniqueness of
solutions. Also, any solution moving from inside C to outside C at a point on
L
would have to be going in an opposite direction to the flow arrows, which is
impossible. Therefore, the next and all subsequent crossings of L by v(t) occur
inside C. This fact implies that the crossings v(t
1
), v(t
2
), v(t
3
), etc., occur in
order on L.
344

8.3 PROOF OF THE P OINCAR
´
E -BENDIXSON T HEOREM
C
L
v(t
2
)
v(t
1
)
u
Figure 8.7 The “In the Bag” Lemma.
A solution is trapped inside the Jordan curve and cannot get out. A simple closed
curve is made up of an orbit segment between successive crossings v(t
1
)andv(t
2
)
of a transversal L, together with the piece L
of L between these points. Once the
orbitentersthis“bag”(atv(t
2
)), it cannot leave. Therefore, any later crossings of L
by the orbit must occur below v(t
2
).
Now let u be a nonequilibrium point in
(v
0
), and let D
␦
(u) be a sufficiently
small
␦
-diamond about u. We will show that
(v
0
) intersects D
␦
(u) in a trajectory
segment S
u
through u. The Invariance Property of
-limit sets provides part of this
picture—namely, that each point of u(t)isin
(v
0
). The Diamond Construction
Lemma tells us that the solution through u must extend across the diamond.
In the following lemma, we prove that the only points of
(v
0
)inD
␦
(u)are
in S
u
.
Lemma 8.13 (The “Locally a Curve” Lemma.) Assume there is a
nonequilibrium point u in
(v
0
). Then there is a
␦
-diamond D
␦
(u)suchthat
(v
0
) 傽 D
␦
(u) is a trajectory segment.
Proof: Let L be a transversal at u, let
␦
be as in the proof of the Diamond
Construction Lemma, and let S
u
be the trajectory segment containing u which
extends across D
␦
(u), as guaranteed by the Diamond Construction. Now for an
arbitrary point z in
(v
0
) 傽 D
␦
(u), there exists a trajectory segment S
z
such that
S
z
contains z, is contained in D
␦
(u), and intersects L at a point z
L
. Let t
1
,t
2
,...
be the times (t
1
⬍ t
2
⬍⭈⭈⭈) for which v(t) 僆 L 傽 D
␦
(u). Then z
L
and u are both
345
P ERIODIC ORBITS AND L IMIT S ETS
limit points of the set 兵v(t
i
)其,i⫽ 1, 2,....Since the points v(t
i
) are monotonic
on L and have both z
L
and u as limit points, it must be that z
L
⫽ u. By uniqueness
of solutions (see Theorem 7.14 of Chapter 7), z is in S
u
.
✎ E XERCISE T8.7
Show that if v
0
僆
(v
0
), then
(v
0
) is either an equilibrium or a periodic
orbit. Specifically, let v ⫽ v(0) be a nonequilibrium point, let L be a transver-
sal at v, and let 兵t
n
其 be an increasing, unbounded sequence of real numbers.
Suppose that v(t
n
)isinL, for each n, and v(t
n
) → v. Then v(t
n
) ⫽ v, for
each n, and v(t) is a periodic orbit.
Corollary 8.14 If u 僆
(v
0
), z 僆
(u), and z is not an equilibrium,
then u is on a periodic orbit.
Proof: In this case, z 僆
(v
0
) by the Transitivity Property. Also, the entire
orbit through u is in
(v
0
) by the Invariance Property. By Lemma 8.13 (“Locally
a curve”), there is a
␦
⬎ 0 such that the only points of
(v
0
)inD
␦
(z)areon
a trajectory segment S
z
through z.Butsincez is in
(u), there are points on
the orbit of u that are arbitrarily close to z. In particular, there are points of u(t)
within D
␦
(z). Since
(v
0
) intersects D
␦
(z)onlyinS
z
, the orbit through u and
the orbit through z must be the same orbit. Thus u is in
(u), and, by Exercise
T8.7, u is a periodic orbit.
Lemma 8.15 (The “Has One, Is One” Lemma.) If
(v
0
) contains a
periodic orbit, then
(v
0
) is a periodic orbit.
Proof: Assume there is a periodic orbit G in
(v
0
). Let z be a point in
(v
0
). Assume further that z is not on G. Let d ⱖ 0 be the (minimum) distance
from z to G. Since
(v
0
) is connected, there must be another point z
1
of
(v
0
)
which is not on G, but which is within distance d 2ofG. Analogously, for
each n ⬎ 1, let z
n
be a point of
(v
0
) which is not on G, but which is within
d 2
n
of G. The sequence 兵z
n
其 necessarily contains infinitely many distinct points,
which must have an accumulation point, since the sequence is bounded. Call
this point u. Then u is on G, but
(v
0
) is not locally a curve in any diamond
neighborhood of u, contradicting Lemma 8.13. Therefore, z is on G.
Now we have all the pieces in place to prove the Poincar
´
e-Bendixson
Theorem.
346
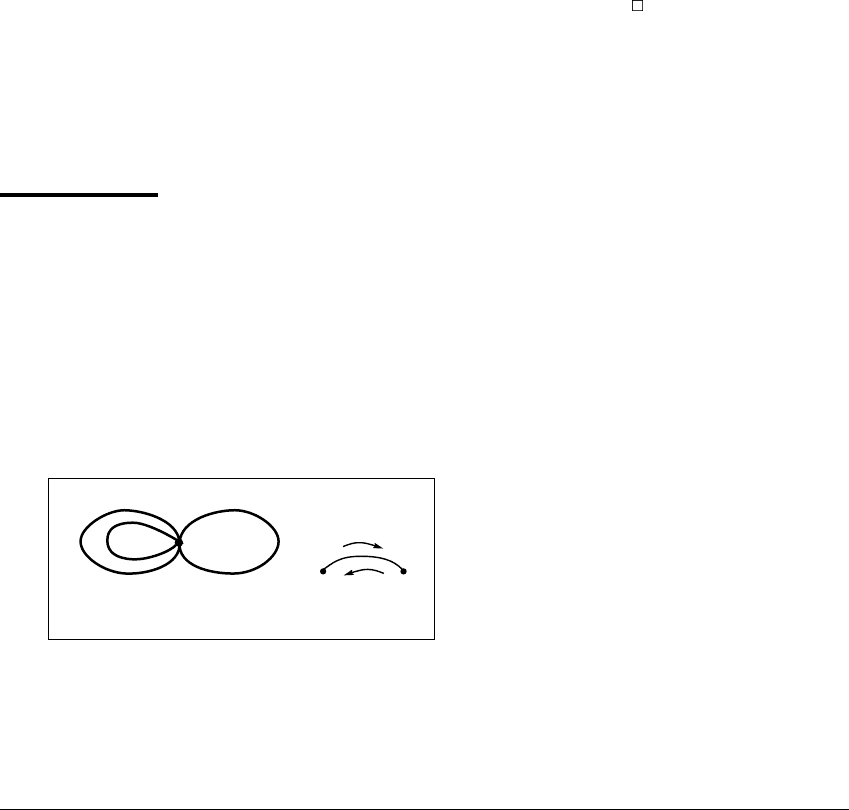
8.3 PROOF OF THE P OINCAR
´
E -BENDIXSON T HEOREM
Proof of Theorem 8.8 (Poincar
´
e-Bendixson Theorem): The
-limit set
(v
0
) is not empty by the Existence Property. We begin by assuming that
(v
0
)
consists entirely of equilibria. Since
(v
0
) is connected (the Connectedness
Property) and since one of our hypotheses is that equilibria are isolated,
(v
0
)
consists of exactly one equilibrium, and case 1 of Theorem 8.8 holds. If case 1
does not hold, there exists a non-equilibrium point u in
(v
0
). Case 3 holds if
(u) is an equilibrium.
The basic idea of the proof is to show that if neither cases 1 nor 3 holds,
then case 2 must hold, and the proof is complete. Suppose, therefore, that cases
1 and 3 do not hold. Then there is a nonequilibrium point u in
(v
0
) for which
there is a nonequilibrium point z in
(u). By Corollary 8.14, the orbit of u is a
periodic orbit. By Lemma 8.15 (“Has one, is one”),
(v
0
) is a periodic orbit.
The Poincar
´
e-Bendixson Theorem does not give a complete characteriza-
tion of limit sets. In particular, some sets that are not ruled out by the theorem
still cannot be limit sets of planar flows. We illustrate this fact in the following
example.
E XAMPLE 8.16
Each of the following figures shows a set consisting of equilibria and con-
necting arcs. Figure 8.8 (a) has one equilibrium and three connecting arcs. The
-limit set of any point in the set shown is the equilibrium. An orbit not shown
must be contained either completely inside one of the loops formed by the con-
necting arcs or completely outside the set of loops. In any case, the entire figure
cannot be an
-limit set. Figure 8.8 (b) has two equilibria and one connecting
arc. The
-limit set of any point in the set shown is one of the two equilibria.
(a) (b)
Figure 8.8 Sets that cannot be limit sets of planar flows.
(a) No single orbit can limit on the set of connecting arcs and equilibrium shown.
(b) This set consists of two equilibria and a connecting arc. If a trajectory has this
figure as its limit set, then the flow must be going in opposite directions on either
side of the connecting arc, an impossibility unless all points on the arc are equilibria.
347
