Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

7.4 NONLINEAR S YSTEMS

L(t

-t

)

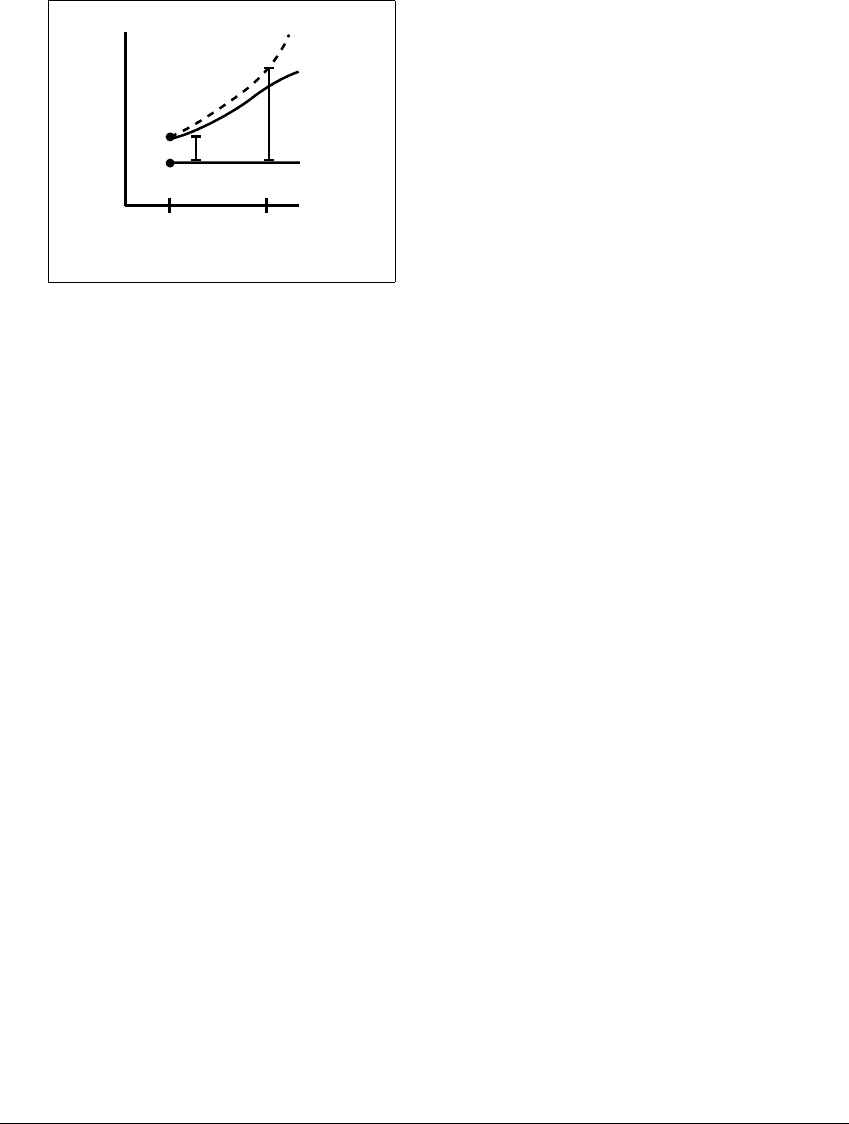
Figure 7.13 The Gronwall inequality.

Nearby solutions can diverge no faster than an exponential rate determined by the

Lipschitz constant of the differential equation.

Higher-order equations often can be transformed into a ﬁrst-order system

of form (7.28). We illustrate the process with the nth-order differential equation

(n)

⫽ f(x,

x,...,x

(n⫺1)

where x

(n)

denotes the nth derivative of the function x(t) with respect to t.Deﬁne

a new set of variables by

⫽ x

⫽

⫽ x

(n⫺1)

These new variables satisfy the ﬁrst-order autonomous system

⫽ x

n⫺1

⫽ x

⫽ f(x

,...,x

)

which is of form (7.28).

297

D IFFERENTIAL E QUATIONS

Unlike linear systems, most nonlinear systems of ordinary differential equa-

tions cannot be solved explicitly, meaning that the solutions cannot be found

through an analytic calculation. Fortunately, much of the stability analysis for

linear systems carries over to the study of equilibria of nonlinear systems.

Recall that an equilibrium of (7.29) is a vector

v in ⺢

such that f

(v) ⫽ 0

for i ⫽ 1,...,n. Again, for a given initial value v

, we denote by F(t, v

)the

solution of (7.29) at time t. While a linear system either has only one equilibrium

(

v ⫽ 0) or has an entire line (or higher-dimensional subspace) of equilibria (see

Exercise T7.6), a nonlinear system can have many isolated equilibria, as the

following exercise illustrates.

✎ E XERCISE T7.8

Verify that the equilibria of the system

x ⫽ y

y ⫽ sin x ⫺ y (7.30)

are (n

␲

, 0) for all integers n.

In order to determine the stability of an equilibrium v of (7.29), we use the

linear map that best approximates f at

v—namely, the Jacobian matrix Df(v)of

partial derivatives evaluated at

v. The Jacobian matrix Df(v) can be expected to

approximate f only in a small neighborhood of

v. Since f(v) ⫽ 0, the approxima-

tion f(

v ⫹

⑀

) ⬇ Df(v)

⑀

holds for small

⑀

. Start a solution w(t) ⫽ F(t, v ⫹

⑀

)from

an initial value

v ⫹

⑀

close to the equilibrium. Then u(t) ⫽ w(t) ⫺ v satisﬁes

˙u ⫽ ˙w ⫽ f(w(t)) ⫽ f(u(t) ⫹

v) ⬇ Df(v)u(t),

at least for short times. The solutions of (7.29) near

v move toward or away

from the equilibrium like the solutions of ˙u ⫽ Df(

v)u. The behavior of the latter

equation, which is linear, depends on the eigenvalues of Df(

v).

Deﬁnition 7.17 An equilibrium

v of ˙v ⫽ f(v) is called hyperbolic if

none of the eigenvalues of Df(

v) has real part 0.

When

v is hyperbolic, the linear part Df(v) completely determines the

stability of

v. When all eigenvalues of Df(v) have nonpositive real parts and

there is at least one eigenvalue with zero real part, then higher-order terms must

be taken into account to determine the stability; that is, it is not sufﬁcient to know

298

7.4 NONLINEAR S YSTEMS

Df(v). Hyperbolic or not, v is unstable if the real part of at least one eigenvalue

of Df(

v) is strictly positive.

Theorem 7.18 Let

v be an equilibrium of ˙v ⫽ f(v). If the real part of each

eigenvalue of Df(

v) is strictly negative, then v is asymptotically stable. If the real part

of at least one eigenvalue is strictly positive, then

v is unstable.

E XAMPLE 7.19

We apply Theorem 7.18 to the following system:

x ⫽ x

⫺ y

y ⫽ xy ⫺ 4. (7.31)

There are two equilibria, (2, 2) and (⫺2, ⫺2). The Jacobian matrix is

Df ⫽



2x ⫺2y



Evaluated at (2, 2), Df has eigenvalues 3 ⫾



7i. Since the real part of the

eigenvalues is ⫹3, (2, 2) is unstable. Evaluated at (⫺2, ⫺2), Df has eigenvalues

⫺3 ⫾



7i. Therefore, (⫺2, ⫺2) is asymptotically stable. A solution with initial

condition (x

) sufﬁciently close to the equilibrium (⫺2, ⫺2) will tend to

(⫺2, ⫺2) as t →

⬁

. Note that Theorem 7.18 does not tell us how close (x

)

must be to (⫺2, ⫺2) for the solution to converge to this equilibrium.

E XAMPLE 7.20

The one-dimensional equation

x ⫽⫺x

(7.32)

has an equilibrium at x ⫽ 0. Since f(x) ⫽⫺x

is a function of one variable, Df is

the derivative f



(x). Since f



(0) ⫽ 0, we cannot use Theorem 7.18 to determine

the stability of x ⫽ 0.

✎ E XERCISE T7.9

Decide whether x ⫽ 0 is an asymptotically stable equilibrium of (7.32).

Solve by separating variables, as in Example 7.4. Does this equation have

unique solutions? Find all solutions that satisfy x(0) ⫽ 1.

299

D IFFERENTIAL E QUATIONS

7.5 MOTION IN A POTENTIAL FIELD

Perhaps the most familiar system that illustrates the concepts of kinetic and

potential energy is the pendulum equation

x ⫹ k sin x ⫽ 0, (7.33)

where x is the angle of the pendulum rod from the vertical and k is the posi-

tive constant k ⫽ g l,wherel is the length of the pendulum rod and g is the

acceleration of gravity. We will set k ⫽ 1 to simplify our analysis.

We are assuming no damping and no external forces aside from gravity. This

equation can be rewritten as a ﬁrst-order system with dependent variables x and

y by setting y ⫽

x. Then

y ⫽

x ⫽⫺sin x, and (7.33) becomes

x ⫽ y

y ⫽⫺sin x. (7.34)

✎ E XERCISE T7.10

(a) Show that the equilibria of (7.34) are 兵(n

␲

, 0) : n ⫽ 0, ⫾1, ⫾2,...其.

(b) Show that Theorem 7.18 identiﬁes (n

␲

, 0) as an unstable (saddle) equi-

librium if n is odd, but tells us nothing if n is even.

Taking a cue from mechanics, we use the principle of Conservation of

Energy: In the absence of damping or any external forces, the system neither

gains nor loses energy. Given an initial condition (x

), the energy function E

remains constant on the orbit F(t, (x

)) for all time t:

(F(t, (x

))) ⫽ 0. (7.35)

Total energy is the sum of kinetic plus potential energies, which for the pendulum

is given by

E(x, y) ⫽ (1 2)y

⫹ 1 ⫺ cos x. (7.36)

The potential energy is minus the integral of the force,



sin udu(the work

required to raise the pendulum from angle 0 to angle x; we have set the mass

of the pendulum bob to 1). To verify (7.35), write (x(t),y(t)) for a solution and

300

7.5 MOTIONINAP OTENTIAL F IELD

compute

E(x(t),y(t)) as

⫽

⳵

⫹

⳵

⫽ (sin x)

x ⫹ y

⫽ (sin x)y ⫹ y(⫺ sin x)

⫽ 0. (7.37)

Notice an interesting aspect of this analysis: We have completed this cal-

culation without knowing the solutions (x(t),y(t)). Equation (7.37) says that

E(x(t),y(t)) ⫽ 0. We conclude in this case that for each solution E(x(t),y(t))

remains constant as t varies. The function E provides a useful partition of the

points (x, y) in the phase plane into individual solution trajectories.

Deﬁnition 7.21 Given a real number c and a function E : ⺢

−→ ⺢, the

set E

⫽ 兵(x, y):E(x, y) ⫽ c其 is called a level curve of the function E.

Notice that the minimum value of the energy function E is 0; hence, E

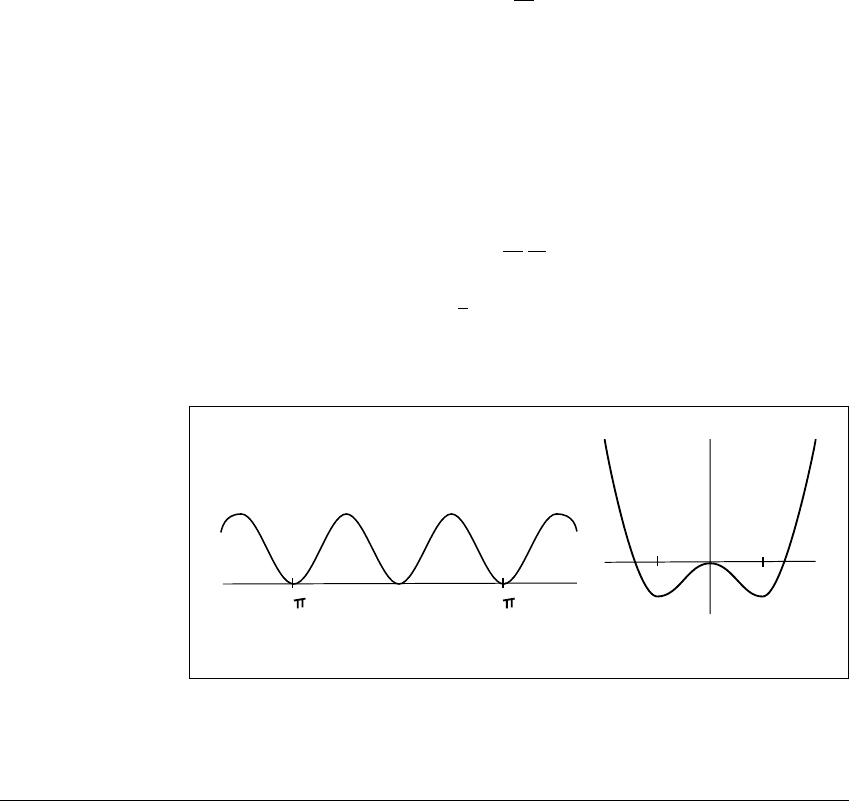
empty for c ⬍ 0. Some of the level curves of E are sketched in Figure 7.14(a).

(a)

(b)

Figure 7.14 Solution curves of the undamped pendulum.

(a) Level curves of the energy function. (b) The phase plane of the pendulum. The

solutions move along level curves; equilibria are denoted by dots. The variable x is

an angle, so what happens at x also happens at x ⫹ 2

␲

. As a results, (a) and (b) are

periodic in x with period 2

␲

301

D IFFERENTIAL E QUATIONS

Keeping in mind that a solution of (7.34) is constrained to one energy level,

we can turn the sketch of level curves into a phase plane of (7.34) merely by

putting arrows on the level curves to indicate the direction of motion, as in

Figure 7.14(b). Notice that solutions above the x-axis move from left to right,

and solutions below the x-axis move from right to left. Of particular interest are

the points in E

. These are precisely the equilibria whose stability could not be

determined by Theorem 7.18: (n

␲

, 0), where n is even. In this case, the phase

plane shows us that these are stable equilibria, since the trajectories of nearby

points lie on closed level curves around the equilibria.

The pendulum equation (7.33) is a special case of the more general equation

x ⫹

⳵

⫽ 0 (7.38)

governing motion in a potential ﬁeld. This is another way of viewing Newton’s

second law of motion—acceleration is proportional to the force, which is the

negative of the gradient of the potential ﬁeld. The potential energy ﬁeld of the

pendulum equation with k ⫽ 1 is a series of potential wells whose minima are

spaced at 2n

␲

for all integers n, shown in Figure 7.15(a).

In the general case we multiply (7.38) by

x and integrate both sides:

x ⫹

⳵

⫽ 0

⫹ P(x) ⫽ E

(7.39)

2-2

P(x)

-1

P(x)

(a) (b)

Figure 7.15 Potential energy functions.

(a) The potential function for the pendulum is P(x) ⫽ 1 ⫺ cos x. There are inﬁnitely

many wells. (b) The double-well potential P(x) ⫽ x

 4 ⫺ x

 2.

302

7.5 MOTIONINAP OTENTIAL F IELD

where E

is a constant of integration. This leads to a simple technique for drawing

phase plane solutions of motion in a potential ﬁeld (7.38). The key is to follow

the difference between total and potential energy as x varies; this difference is the

kinetic energy

 2. In Figure 7.16(a) we illustrate a typical single-well potential

energy function. According to (7.39), for a ﬁxed energy level E

, the difference

⫺ P(x) is proportional to the square of the velocity

x. As x increases from x

(where P ⫽ E

)tox

, the derivative

x increases from 0 to some maximum value

(at the minimum of P) and then decreases to 0 at x

. The phase plane solution

at energy level E

is depicted in Figure 7.16(b). Solutions to single-well potential

problems in the absence of damping are periodic orbits.

Figure 7.15(b) shows the double-well potential P(x) ⫽ x

 4 ⫺ x

 2, which

by substitution in (7.38) leads to the double-well Dufﬁng equation

x ⫺ x ⫹ x

⫽ 0. (7.40)

Most of the solutions are periodic orbits. If the initial conditions (x,

x) are set so

that the total energy E

⫽ P(x) ⫹

 2 is less than zero, then the orbit is trapped

in one of the two potential wells. If E

⬎ 0, orbits will move periodically through

both wells, reaching a maximum of P(x) ⫽ E

on the far sides of the wells.

As might be expected from our experiences with the pendulum equation

throughout this book, the Dufﬁng equation becomes even more interesting if

P(x)

(a) (b)

Figure 7.16 Drawing phase plane curves from the potential.

(a) Graph of the potential energy function P(x). Each trajectory of the system is

trapped in a potential energy well. The total energy

 2 ⫹ P(x) is constant for

trajectories. As a trajectory with ﬁxed total energy E

tries to climb out near x

or x

, the kinetic energy

 2 ⫽ E

⫺ P(x) goes to zero, as the energy E converts

completely into potential energy. (b) A periodic orbit results: The system oscillates

between positions x

and x

303

D IFFERENTIAL E QUATIONS

damping and periodic forcing are added. With damping, (7.38) becomes

x ⫹ c

x ⫹

⳵

⫽ 0. (7.41)

Energy is no longer conserved, for the time derivative of total energy E ⫽

 2 ⫹

P(x)is

E ⫽

x ⫹

⳵

⫽



⫺c

x ⫺

⳵



⫹

⳵

⫽⫺c

. (7.42)

Total energy decreases along orbits. Typical orbits will move progressively slower

and stop at the bottom of one of the two energy wells. See the Computer Experi-

ment 7.3 and Section 9.5 for the results of periodically forcing the Dufﬁng double

well oscillator.

✎ E XERCISE T7.11

Not all orbits of (7.41) are attracted to the bottom of one of the wells.

Describe as many as you can that end up elsewhere.

➮ COMPUTER EXPERIMENT 7.3

Write a computer program to plot numerical solutions of the forced damped

double-well Dufﬁng oscillator

x ⫹ 0.1

x ⫺ x ⫹ x

⫽ 2sint in the (x,

x)-plane. In

particular, locate and plot the attracting periodic orbit of period 2

␲

and the two

attracting periodic orbits of period 6

␲

that lie in the region ⫺5 ⱕ x,

x ⱕ 5.

7.6 LYAPUNOV FUNCTIONS

The basic idea of using energy-like functions to investigate the dynamics of

solutions can be applied to equations more general than (7.38). The theory

of Lyapunov functions, a generalization of potential energy functions, gives us

a global approach toward determining asymptotic behavior of solutions. The

main stability result of this chapter, Theorem 7.18, tells about local stability. In

304

7.6 LYAP U N OV F UNCTIONS

the neighborhood of an equilibrium, solution trajectories are attracted to the

equilbrium if the eigenvalues of the linear part of the equation have negative

real part. Lyapunov functions can tell us that initial values from a large region

converge to an equilibrium. In addition, they can sometimes be used to determine

stability of equilibria where the eigenvalues of Df have real part 0, as in Example

7.20.

Let v(t) ⫽ (x

(t),...,x

(t)) be a solution of the n-dimensional system

(7.29) of differential equations. Suppose we pick a real-valued function of the

state, E(v), which we would like to consider to be the energy of the system when

it is in the state v. To measure the time rate of change of E along a solution

trajectory, we need to take the derivative of E with respect to t. Using the chain

rule and the differential equation, we ﬁnd:

E(x

,...,x

) ⫽

⳵

⫹⭈⭈⭈⫹

⳵

⫽

⳵

,...,x

) ⫹⭈⭈⭈⫹

⳵

,...,x

). (7.43)

That is, the derivative of E with respect to time can be expressed in terms of the

differential equation itself—the solutions do not explicitly appear in this formula.

The derivative

E(v) measures the rate of change of E along a solution

trajectory of (7.29) as it passes through the point v. In the example of the

pendulum, we found

E ⫽ 0 along trajectories. Using the total energy function

to determine the stability of equilibria for a conservative system (one in which

energy is conserved) is an example of the technique of Lyapunov functions.

Deﬁnition 7.22 Let

v be an equilibrium of (7.29). A function E : ⺢

→

⺢ is called a Lyapunov function for

v if for some neighborhood W of v,the

following conditions are satisﬁed:

1. E(

v) ⫽ 0, and E(v) ⬎ 0 for all v ⫽ v in W,and

E(v) ⱕ 0 for all v in W.

If the stronger inequality



E(v) ⬍ 0 for all v ⫽ v in W

holds, then E is called a strict Lyapunov function.

Condition (1) says that

v is at the bottom of the well formed by the graph

of the Lyapunov function E, as shown in Figures 7.17(a) and (b). Condition (2)

says that solutions can’t move up, but can only move down the side of the well

305

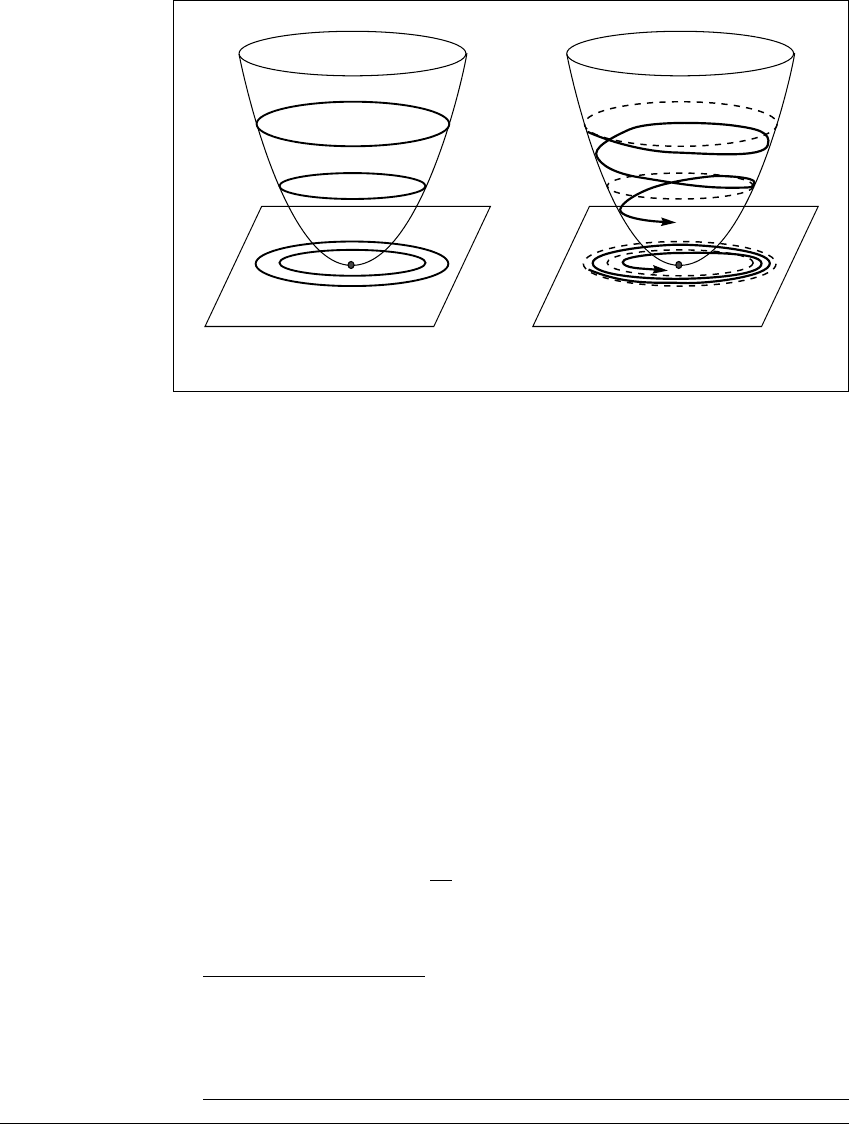
D IFFERENTIAL E QUATIONS

(a) (b)

Figure 7.17 Behavior of solution trajectories with a Lyapunov function.

The bowl in the ﬁgure is the graph of E. In both parts, we plot E (v(t)) versus the

solution trajectory v(t), which lies in the horizontal plane. (a) An equilibrium is

at the critical point of the graph of the Lyapunov function E. The equilibrium is

(Lyapunov) stable, since any nearby solution cannot go uphill, and can move away

only a bounded distance dictated by its original energy level. (b) For a strict Lya-

punov function, energy of solutions must continually decrease toward zero, cutting

through energy level sets. The equilibrium is asymptotically stable.

or stay level. Figure 7.17(b) shows a strict Lyapunov function, where energy must

keep decreasing toward the equilibrium.

In order to verify the conditions for a Lyapunov function, it is helpful to

use (7.43). For example, the one-dimensional equation

x ⫽ ax,wherea ⬍ 0, has

the Lyapunov function E(x) ⫽ x

. It is clear that condition (1) is satisﬁed for the

equilibrium x ⫽ 0. Moreover, (7.43) shows

E(x) ⫽

⳵

f(x) ⫽ (2x)(ax) ⫽ 2ax

⬍ 0,

which veriﬁes (2’). Therefore E(x) ⫽ x

is a strict Lyapunov function.

✎ E XERCISE T7.12

Show that for each even integer n, total energy E(x, y) ⫽ (1 2)y

⫹ 1 ⫺ cos x

is a Lyapunov function for the equilibria (n

␲

, 0) of (7.34).

306