Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

P ERIODIC ORBITS AND L IMIT S ETS

inside the inner orbit. This is the picture we might expect following a subcritical

Hopf bifurcation, discussed in Chapter 11.

A magniﬁcation of this picture is shown in Figure 8.11(b). The pulse moves

the trajectory from point A on the stable periodic orbit to point B, after which

the system dynamics causes the trajectory to spiral in to the equilbrium.

Almost two decades after this set of experiments, it is widely suspected that

coexisting attractors are one of nature’s principal means of efﬁcient regulation and

communication. Once the periodic (spiking) behavior of such a cell is established,

it is stable against small noise perturbations. The cell can be used as a timekeeper or

pacemaker for a ﬁnite duration, while prepared to turn off instantly when signalled

to stop. Although this research involved neuronal cells, the basic principle is

probably more widespread. (Jalife and Antzelevitch, 1979) is a contemporaneous

article on coexisting periodic and equilibrium attractors in cardiac tissue.

358

C HAPTER N INE

Chaos in Differential

Equations

9.1 THE LORENZ ATTRACTOR

In the late 1950s, a meteorologist at MIT named Edward Lorenz acquired a Royal-

McBee LGP-30 computer. It was the size of a refrigerator carton and contained

16KB of internal memory in a thicket of vacuum tubes. It could calculate at the

rate of 60 multiplications per second. For the time, it was a staggering cache of

computational power to be assigned to a single scientist.

Lorenz set the new computer to work calculating approximate solutions of

a system of 12 differential equations that model a miniature atmosphere. The sta-

tistical weather forecasting community at the time was developing sophisticated

linear methods for prediction. Lorenz had come to the conclusion that there had

to be a fundamental factor, as yet unacknowledged, limiting the success of linear

359

C HAOS IN D IFFERENTIAL E QUATIONS

models in weather prediction. He was trying to demonstrate this point by ﬁnding

solutions to his miniature atmosphere that were not periodic nor asymptotically

periodic; in short, trajectories that would confound linear prediction techniques.

The atmosphere model included many parameters that he did not know

how to set. The use of a computer allowed him to explore parameter space in a

way that would have been impossible otherwise. He tinkered, for example, with

parameters that affected the way the atmosphere was heated from below by the

(sun-warmed) oceans and continents. The LGP-30 was soon producing longer

and longer trajectories that seemed to be aperiodic. Moreover, they shared many

qualitative features with real weather, such as long persistent trends interrupted

by rapid changes. The computer printed out the trajectories on rolls of paper at

its top printing speed of 6 lines of numbers per minute.

The ﬂash of insight came from an unexpected direction. To speed up the

output, Lorenz altered the program to print only three signiﬁcant digits of the

approximate solution trajectories, although the calculation was being done inter-

nally using several more digits of accuracy. After seeing a particularly interesting

computer run, he decided to repeat the calculation to view it in more detail. He

typed in the starting values from the printed output, restarted the calculation,

and went down the hall for a cup of coffee. When he returned, he found that the

restarted trajectory had gone somewhere else entirely—from initial conditions

that were unchanged in the ﬁrst three signiﬁcant digits. Originally suspecting a

vacuum tube failure, he was surprised to ﬁnd that the discrepancy occurred grad-

ually: First in the least signiﬁcant decimal place, and then eventually in the next,

and so on. Moreover, there was order in the discrepancy: The difference between

the original and restarted trajectories approximately doubled in size every four

simulated days. Lorenz concluded that he was seeing sensitive dependence on

initial conditions. His search for aperiodicity had led to sensitive dependence.

Realizing the wide scope of the discovery, Lorenz tried to reduce the com-

plexity of the 12-equation model, to verify that the effect was not simply an

idiosyncracy of one particular model. Due to the Poincar

e-Bendixson Theorem,

a chaotic solution could not be found in a model with fewer than 3 differential

equations, but if the effect were general, it should be present in smaller, simpler

systems than the 12-equation model. He would not succeed in the reduction of

this particular miniature atmosphere model until 20 years later.

In the meantime, on a 1961 visit to Barry Saltzman of the Travelers Insur-

ance Company Weather Center in Hartford, Connecticut, Lorenz was shown a

7-equation model of convective motion in a ﬂuid heated from below and cooled

from above. Saltzman’s seven equations were themselves the reduction from a set

of partial differential equations describing Rayleigh-B

enard convection, which

360

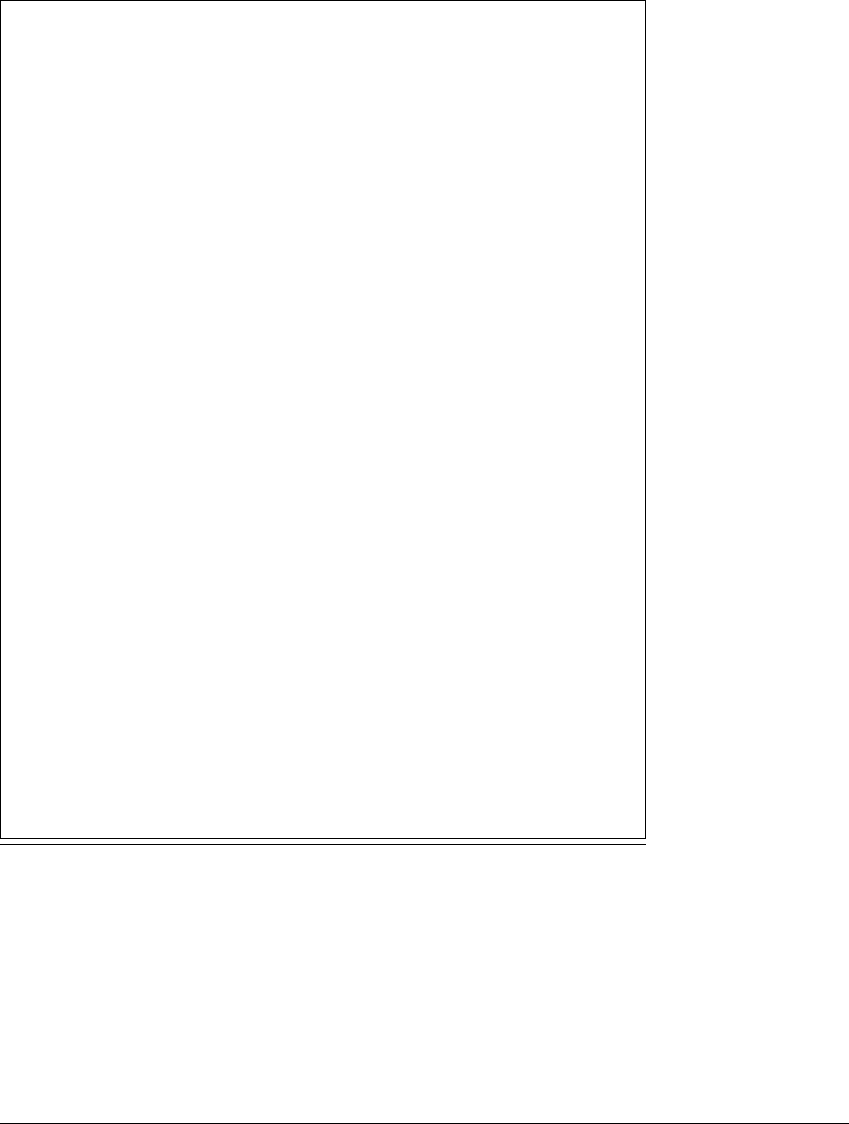
9.1 THE L ORENZ ATTRACTOR

T HE C OMPUTER A GE

Lorenz used his computer to explore parameter space. Eventually,

he was able to ﬁnd the settings in the meteorological model that

corresponded to a chaotic attractor. This was one of the early successes

of computer simulation.

In fact, the motivating interest of John Mauchly, a physics profes-

sor in Pennsylvania who together with John Eckert built the ﬁrst

general-purpose electronic digital computer in 1946, was the solution

of complex meteorological equations. The Electronic Numerical In-

tegrator and Computer (ENIAC), weighing 30 tons and containing

18,000 vacuum tubes, ﬁrst operated on St. Valentine’s Day, 1946. It is

said that ENIAC, in its 10 years of operation, did more ﬂoating-point

calculations than had been done by the entire human race before

1946.

A stunning public demonstration of the use of computers occurred

in 1969, when three astronauts traveled to the moon and back. Ad-

vances in computer hardware and software provided the telemetry

and communications necessary for the ﬂight. Progress in miniaturiza-

tion allowed computers to be aboard the lunar lander to assist in the

descent to the moon.

Miniaturization problems were solved by the invention of the inte-

grated circuit, and by the 1980s cheap computation was generally

available in the form of personal computers. In the 1990s, the embed-

ding of computing chips in automobiles, toasters, and credit cards is

routine. The modern car has more on-board computing power than

the lunar lander of 1969.

study how heat rises through a ﬂuid like air or water. Assume that there are two

parallel horizontal plates with a ﬂuid between them. Gravity is in the downward

direction, and the temperature of the lower plate, T

, is maintained at a higher

value than temperature of the upper plate T

, as shown in Figure 9.1.

A possible equilibrium of this system is one in which the ﬂuid is at rest

and heat is transported upward via thermal conduction. Lord Rayleigh studied

the linear stability of this equilibrium and found that if the difference in temper-

ature T

⫺ T

exceeds a critical value, then the equilibrium becomes unstable,

361

C HAOS IN D IFFERENTIAL E QUATIONS

cooling

heating

Figure 9.1 Rayleigh-B

enard convection.

The way in which heat rises in a ﬂuid from the lower warm plate to the higher cool

plate depends on the temperature difference T

⫺ T

of the plates. If the difference

is small, heat is transferred by conduction. For a larger difference, the ﬂuid itself

moves, in convection rolls.

and convection rolls appear. Further instability occurs as T

⫺ T

is increased.

Considering variations in only two dimensions, (Saltzman, 1962) derived a set of

nonlinear ordinary differential equations by expanding the solution functions in

a Fourier series, substituting the series into the original governing set of partial

differential equations, and truncating the inﬁnite sum to a ﬁnite number of terms.

Lorenz then set all but three Fourier coefﬁcients equal to zero, and obtained a

system of three ordinary differential equations:

x ⫽⫺

␴

x ⫹

␴

y ⫽⫺xz ⫹ rx ⫺ y (9.1)

z ⫽ xy ⫺ bz.

In this highly idealized model of a ﬂuid, the warm ﬂuid below rises and the cool

ﬂuid above sinks, setting up a clockwise or counterclockwise current. The Prandtl

number

␴

, the Rayleigh (or Reynolds) number r,andb are parameters of the

system. The variable x is proportional to the circulatory ﬂuid ﬂow velocity. If

x ⬎ 0, the ﬂuid circulates clockwise while x ⬍ 0 means counterclockwise ﬂow.

The width of the ﬂow rolls in Figure 9.1 is proportional to the parameter b.The

variable y is proportional to the temperature difference between ascending and

descending ﬂuid elements, and z is proportional to the distortion of the vertical

temperature proﬁle from its equilibrium (which is linear with height).

For

␴

⫽ 10, b ⫽ 8 3, Lorenz found numerically that the system behaves

“chaotically” whenever the Rayleigh number r exceeds a critical value r ⬇ 24. 74;

that is, all solutions appear to be sensitive to initial conditions, and almost all

of them are apparently neither periodic solutions nor convergent to periodic

solutions or equilibria.

362

9.1 THE L ORENZ ATTRACTOR

✎ E XERCISE T9.1

Show that equations (9.1) exhibit the following symmetry: The equa-

tions are unchanged when (x, y, z)isreplacedby(⫺x, ⫺y, z). As a result,

if (x(t),y(t),z(t)) is a solution, then so is (⫺x(t), ⫺y(t),z(t)).

✎ E XERCISE T9.2

Find all equilibrium points of the Lorenz equations (9.1).

For the rest of the discussion, we will assume that

␴

⫽ 10, b ⫽ 8 3, and r is

greater than 0. The equilibrium (0, 0, 0) exists for all r, and for r ⬍ 1, it is a stable

attractor. The origin corresponds to the ﬂuid at rest with a linear temperature

proﬁle, hot at the bottom and cool on top. Two new equilibria exist for r ⱖ 1, C

⫹

⫽

(



b(r ⫺ 1),



b(r ⫺ 1),r ⫺ 1) and C

⫺

⫽ (⫺



b(r ⫺ 1), ⫺



b(r ⫺ 1),r ⫺ 1),

representing steady convective circulation (clockwise or counterclockwise ﬂow).

This pair of equilibria branch off from the origin at r ⫽ 1 and move away as r

is increased. For r ⱖ 1, the origin is unstable. The two equilibria representing

convective rolls, C

⫹

and C

⫺

, are stable at their birth at r ⫽ 1 and remain stable

for r ⬍ r

⫽ 24

⬇ 24.74. For r ⬎ r

, all three equilibria are unstable.

For r in a range of values greater than r

ⴱ

⬇ 24. 06, the chaotic attractor

shown in Figure 9.2 is observed numerically. This ﬁgure depicts the orbit of a

single initial condition, with several different rotated views. We say that there is

a numerically observed attractor since the choice of almost any initial condition

in a neighborhood of the depicted set results in a similar ﬁgure (after disregarding

an initial segment of the orbit). This observation also indicates that a generating

orbit is dense.

Lyapunov numbers and exponents can be assigned to orbits of autonomous

differential equations in a straightforward way: They are the Lyapunov numbers

and exponents of the time-1 map of the ﬂow. See Section 9.6 for a discussion.

Calculations indicate that a typical orbit of the Lorenz attractor has one positive

Lyapunov exponent, calculated to be approximately 0.905 ⫾ 0.01.

➮ COMPUTER EXPERIMENT 9.1

An important feature of the Lorenz attractor is its robustness—it persists in

the basic form of Figure 9.2 over a signiﬁcant range of parameters. Fix r ⫽ 28 and

363

C HAOS IN D IFFERENTIAL E QUATIONS

plot the set of (

␴

,b) in the plane for which there exists an apparently chaotic

attractor.

As Figure 9.2 illustrates, the attractor occupies a very thin subset of ⺢

. We

know, of course, that it cannot be constrained to a two-dimensional subset due to

(a) (b) (c)

(d) (e) (f)

(g) (h) (i)

Figure 9.2 Several rotated views of the Lorenz attractor with

ⴝ 28.

In frames (a)–(c), the attractor is tipped up (rotated about the horizontal x-axis)

until the left lobe is edge-on. In frames (d)–(f), the attractor is rotated to the left,

around a vertical line. In frames (g)–(i), more rotation about a horizontal line.

364

9.1 THE L ORENZ ATTRACTOR

Attractor

[⫺

⬁

, 1.00] (0, 0, 0) is an attracting equilibrium

[1.00, 13.93] C

⫹

and C

⫺

are attracting equilibria; the origin is unstable

[13.93, 24.06] Transient chaos: There are chaotic orbits

but no chaotic attractors

[24.06, 24.74] A chaotic attractor coexists

with attracting equilibria C

⫹

and C

⫺

[24.74, ?] Chaos: Chaotic attractor exists but C

⫹

and C

⫺

are no longer attracting

Table 9.1 Attractors for the Lorenz system (9.1).

For

␴

⫽ 10, b ⫽ 8 3, a wide range of phenomena occur as r is varied.

the Poincar

e-Bendixson Theorem. A trajectory will appear to spiral out around

one equilibrium, C

⫹

or C

⫺

, until its distance from that equilibrium exceeds some

critical distance. Thereafter, it spirals about the other equilibrium with increasing

amplitude oscillations until the critical distance is again exceeded.

Other phenomena are observed in different parameter ranges. For r values

between approximately 24.06 and 24.74, a stable chaotic attractor and stable

attracting equilibria coexist. The fate of the system depends upon whether initial

conditions lie in the basin of attraction of the chaotic attractor or one of the

equilibria. For some much larger values of r, (r ⬎ 50), Lorenz has found stable

periodic orbits, and for such values no chaotic attractor is observed.

The observations of the phenomena of the Lorenz attractor were ﬁrst de-

scribed in detail in the original article by (Lorenz, 1963) and later expanded

by (Kaplan and Yorke, 1979). C. Sparrow wrote an entire book about these

observations and theoretical aspects of the Lorenz system (Sparrow, 1982). The

Rayleigh–B

enard convection geometry that originally motivated the Lorenz equa-

tions does not follow the route to chaos just described because of the three-

dimensional nature of that geometry. The ﬂuid moves in more complicated pat-

terns involving swirling behavior on many length scales. This is ignored in the

simpliﬁcation of the convection to two spatial dimensions, but plays a crucial

role in the transition to time-dependent motion. In the meantime it has been

suggested that the Lorenz equations might better describe convective ﬂow in

a closed circular tube. The tube forces the ﬂuid to be constrained to move in

large circular patterns, so the Lorenz equations are more appropriate. Derivation

of the equations from this model is given in (Yorke, Yorke, and Mallet-Paret,

1979).

365

C HAOS IN D IFFERENTIAL E QUATIONS

9.2 STABILITY IN THE LARGE,INSTABILITY

IN THE

SMALL

In this section we discuss three typical properties of chaotic attractors and show

how they are illustrated by the Lorenz attractor. More precisely, we will discuss

attractors that are dissipative (volume-decreasing), locally unstable (orbits do not

settle down to stationary, periodic, or quasiperiodic motion) and stable at large

scale (in the sense that they have a trapping region).

First is the property of volume contraction, or dissipation. We have seen

this basic principle before: With area-contracting maps of the plane, it is common

to have an expanding local direction as well as a perpendicular, contracting local

direction so that area ends up being decreased by the map. If the product of the

contraction rate and expansion rate is less than one, then the attractor will have

zero area.

The attractors we study in this chapter have the same property, although

in each case the phase space is three-dimensional, so we talk about volume

decreasing. The Lorenz equations decrease volume with a factor of e

⫺

␴

⫺1⫺b

⬇

0.00000116 each time unit. We will show where this expression comes from in

Section 9.6.

The second important property is local instability. The typical trajectory

of the Lorenz attractor shown in Figure 9.2 is evidently a chaotic trajectory,

meaning that it has a positive Lyapunov exponent and is not asymptotically

periodic. Neither of these statements can be rigorously proved at the present

time. In place of a rigorous proof we will show evidence that we hope will be

persuasive if not convincing.

Best estimates for the Lyapunov exponents of the Lorenz trajectory shown in

Figure 9.2 are

␭

⫽ 0.905 ⫾ 0.005,

␭

⫽ 0.0, and

␭

⫽⫺14.57 ⫾ 0.01. We will

discuss how these numbers were computed in Section 9.6. The sum of the three

Lyapunov exponents must be ⫺(

␴

⫹ 1 ⫹ b) ⫽⫺13

. The Lyapunov numbers are

found by exponentiating the Lyapunov exponents, and are L

⬇ 2.47, L

⫽ 1, and

⬇ 0.00000047. Therefore the distance between a pair of points that start out

close together on the Lorenz attractor increases by the factor of ⬇ 2.47 per time

unit (often called a “second”). One time unit is roughly the time required for a

typical loop of a Lorenz trajectory. Volume decreases by a factor of 0.00000116 per

time unit. This explains the extreme ﬂatness of the Lorenz attractor. It is almost a

two-dimensional surface. The Lyapunov dimension is 2 ⫹ 0.905 14.57 ⬇ 2.062.

To argue that the attractor is not periodic, Lorenz decided to examine the

behavior of successive maxima of the z-coordinate of the trajectory. This is the

366

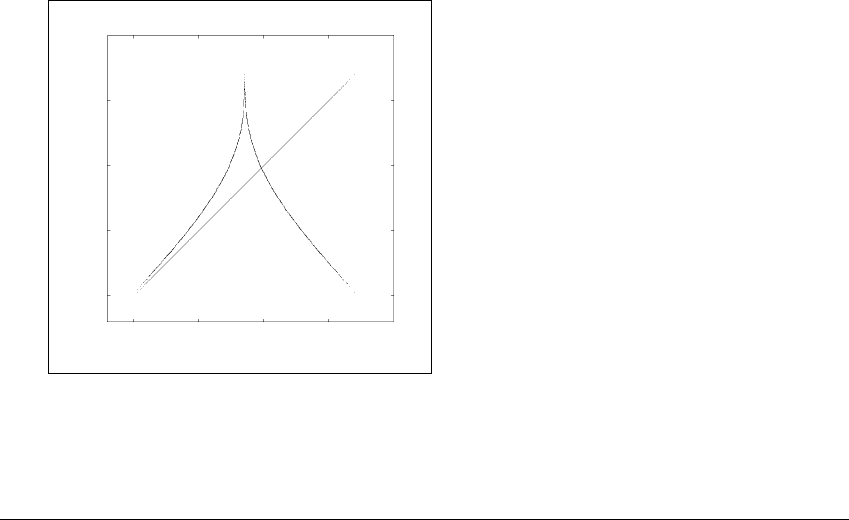
9.2 STABILITY IN THE L ARGE,INSTABILITY IN THE S MALL

vertical direction in Figure 9.2(a). He made an interesting discovery: If one plots

the next vertical maximum z

n⫹1

as a function f of the current z

, a very simple

diagram emerges. It is shown in Figure 9.3. The result is almost a curve; there is

a tiny thickness to the graph. For practical purposes, we can view Figure 9.3 as a

one-dimensional map.

Lorenz’s idea was to reduce the question of whether the Lorenz attractor is

periodic to the same question about the one-dimensional map. The map f has

similarities to a tent map; the absolute value of the slope is greater than one at

all points. Any periodic orbit must be unstable, since the derivative of f

at any

point of the periodic orbit must be a product of numbers whose magnitudes are

greater than one. The shape of the z-maximum return map makes it impossible

for an attracting periodic orbit to exist.

Viewing the attractor by its z-maxima gives us a way to draw a bifurcation

diagram of the Lorenz system as we change a parameter. Fixing

␴

⫽ 10 and

b ⫽ 8 3, we look at the attractors of the Lorenz system for a range of r values

by plotting the attractors of the z-maxima return map. As r varies, the shape of

the map in Figure 9.3 changes. For some r there are periodic attractors. Figure

9.4 shows the results for 25 ⱕ r ⱕ 325. The left side of the graph corresponds

to the traditional Lorenz attractor at r ⫽ 28. Windows corresponding to periodic

attractors are clearly visible. At r ⫽ 400 there is a single loop periodic orbit

n⫹1

28 z

Figure 9.3 Successive maxima of

-coordinate of Lorenz attractor.

Each plotted dot on the tent-like map is a pair (z

n⫹1

)ofmaximumz-coordinates

of loops of the trajectory, one following the other. The nearly one-dimensional

nature of the map arises from the very strong volume contraction.

367