Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS IN D IFFERENTIAL E QUATIONS

400

25 r 325

Figure 9.4 Bifurcation diagram of the Lorenz tent map.

The asymptotic behavior of the tent map of Figure 9.3 is plotted as a function of

the bifurcation parameter r. The points plotted above each r correspond to the

z-maxima of the orbit, so that 1 point means a period-T orbit, 2 points correspond

to a period-2T orbit, and so on.

that attracts all initial conditions. As r is decreased from 400, there is a period-

doubling bifurcation that results in a double-loop attractor, one with two different

z-maxima before returning to repeat the orbit. As r is decreased further, the double

loop again period-doubles to a loop with four different z-maxima, and so on. This

is a period-doubling cascade, which we will discuss in detail in Chapter 12.

Finally, we discuss global stability, which means simply that orbits do not

diverge to inﬁnity, but stay trapped in some ﬁnite ball around the origin. Lorenz

showed that all solutions to the equations (9.1) were attracted into a ball. He did

this by ﬁnding a function E(x, y, z) that is decreasing along any trajectory that

meets the boundary of the bounded region deﬁned by E ⱕ C, for some constant C.

This means it can never leave the region, since E must increase to get out.

Lemma 9.1 (Existence of a trapping region.) Let u(t) ⫽ (x(t),y(t),z(t)),

and let E(u) be a smooth real-valued function with the property that E(u) →

⬁

368

9.2 STABILITY IN THE L ARGE,INSTABILITY IN THE S MALL

⫺18 x 18

Figure 9.5 Transient chaos in the Lorenz equations.

A trajectory of the Lorenz system has been plotted using b ⫽ 8 3and

␴

⫽ 10,

the same values Lorenz used, but here r ⫽ 23. When r ⬍ r

⬇ 24.06 there is

no longer a chaotic attractor, but if r ⬎ 13.926 ... there are chaotic trajectories,

producing “transient chaos”, where the trajectory behaves like a chaotic trajectory

and then suddenly leaves the chaotic region. In this case, after a long transient time

it ﬁnally approaches one of the asymptotically stable equilibrium points. The part

of this picture that looks like the Lorenz attractor is actually the early part of the

trajectory; the black spot shows the trajectory spiraling down to the equilibrium

point. For r ⫽ 23, the mean lifetime is about 300 (which means that the variable

z(t) oscillates slightly over 300 times on the average before the decay sets in. For

r ⫽ 23.5, the mean number of oscillations is over 2400. As r is chosen closer to the

critical value r

, the number of oscillations increases so that it becomes increasingly

difﬁcult to distinguish between a chaotic attractor and transient chaos. Even at

r ⫽ 23.0, there are chaotic trajectories that oscillate chaotically forever, never

spiraling in to the equilibrium.

369

C HAOS IN D IFFERENTIAL E QUATIONS

as ||u|| →

⬁

. Assume that there are constants a

, b

, c, for i ⫽ 1, 2, 3, where

⬎ 0 such that for all x, y, z,

E(x, y, z) ⱕ⫺a

⫺ a

⫹ b

x ⫹ b

y ⫹ b

z ⫹ c. (9.2)

Then there is a B ⬎ 0 such that every trajectory u(t) satisﬁes |u(t)| ⱕ B for all

sufﬁciently large time t.

✎ E XERCISE T9.3

Provide a proof of the Trapping Region Lemma 9.1.

We will try to apply the Lemma to the Lorenz equations. A typical ﬁrst

guess for a function E that will satisfy (9.2) is E(x, y, z) ⫽

⫹ y

⫹ z

). Then

E ⫽ x

x ⫹ y

y ⫹ z

z. Using the Lorenz system to provide

z yields

x ⫽

␴

xy ⫺

␴

y ⫽ rxy ⫺ y

⫺ xyz

z ⫽⫺bz

⫹ xyz. (9.3)

The sum of these terms includes (

␴

⫹ r)xy, which is not allowed in (9.2). How-

ever,

z does have such a term. If we change to E(x, y, z) ⫽

⫹ y

⫹ (z ⫺

␴

⫺

), we can replace the bottom line above by

(z ⫺

␴

⫺ r)

z ⫽⫺(

␴

⫹ r)xy ⫺ bz

⫹ xyz ⫹ b(

␴

⫹ r)z.

Then

E ⫽⫺

␴

⫺ y

⫺ bz

⫹ b(

␴

⫹ r)z, which has the form required by Lemma

9.1. We conclude that all trajectories of the Lorenz system enter and stay in some

bounded ball in three-dimensional space.

9.3 THE R

OSSLER ATTRACTOR

The Lorenz attractor has been studied in detail because it is a treasure trove of

interesting phenomena. It was the ﬁrst widely known chaotic attractor from a

set of differential equations. The equations are simple, yet many different types

of dynamical behavior can be seen for different parameter ranges. Subsequently,

many other chaotic systems of differential equations have been identiﬁed. In this

section and the next, we discuss two other systems that produce chaotic attractors.

There is a symmetry in the Lorenz attractor about the z-axis, as seen in

Figure 9.2, and as explained by Exercise T9.1. While this symmetry undoubtedly

370

9.3 THE R

OSSLER ATTRACTOR

contributes to the beauty of the Lorenz attractor, it should be noted that symmetry

is not a necessity. The German scientist O. R

ossler found a way to create a chaotic

attractor with an even simpler set of nonlinear differential equations.

The R

ossler equations (R

ossler, 1976) are

x ⫽⫺y ⫺ z

y ⫽ x ⫹ ay

z ⫽ b ⫹ (x ⫺ c)z. (9.4)

For the choice of parameters a ⫽ 0.1,b ⫽ 0.1, and c ⫽ 14, there is an apparent

chaotic attractor, shown in Figure 9.6. The Lyapunov exponents for this attractor

have been measured by computational simulation to be approximately 0.072, 0

and ⫺13.79. The corresponding Lyapunov dimension is 2.005. R

ossler primarily

considered a slightly different set of parameters, a ⫽ 0.2,b ⫽ 0.2, and c ⫽ 5.7,

but the properties are not much different for these values.

We can understand much of the behavior of the R

ossler equations since

all but one of the terms are linear. We begin by looking at the dynamics in the

xy-plane only. Setting z ⫽ 0 yields

x ⫽⫺y

y ⫽ x ⫹ ay. (9.5)

The origin is an equilibrium. To ﬁnd its stability, we calculate the eigenvalues of

the Jacobian matrix at

v ⫽ (0, 0)

Df(0, 0) ⫽



0 ⫺1

1 a



to be (a ⫾



⫺ 4) 2. For a ⬎ 0, there is at least one eigenvalue with positive

real part, so the origin is unstable, for the dynamics in the xy-plane. For 0 ⬍ a ⬍ 2,

the eigenvalues are complex, implying a spiraling out from the origin along the

xy-plane.

Now let’s make the assumption that 0 ⬍ a ⬍ 2andb, c ⬎ 0, and turn the

z-direction back on. Assume for the moment that z ⬇ 0, so that we are near the

xy-plane. The orbit will spiral out from the origin and stay near the xy-plane

as long as x is smaller than c, since the third equation in (9.4) has a negative

coefﬁcient for z.Whenx tries to pass c,thez-variable is suddenly driven to

large positive values. This has the effect of stopping the increase of x because of

the negative z-term in the ﬁrst equation of (9.4). The back and forth damping

371

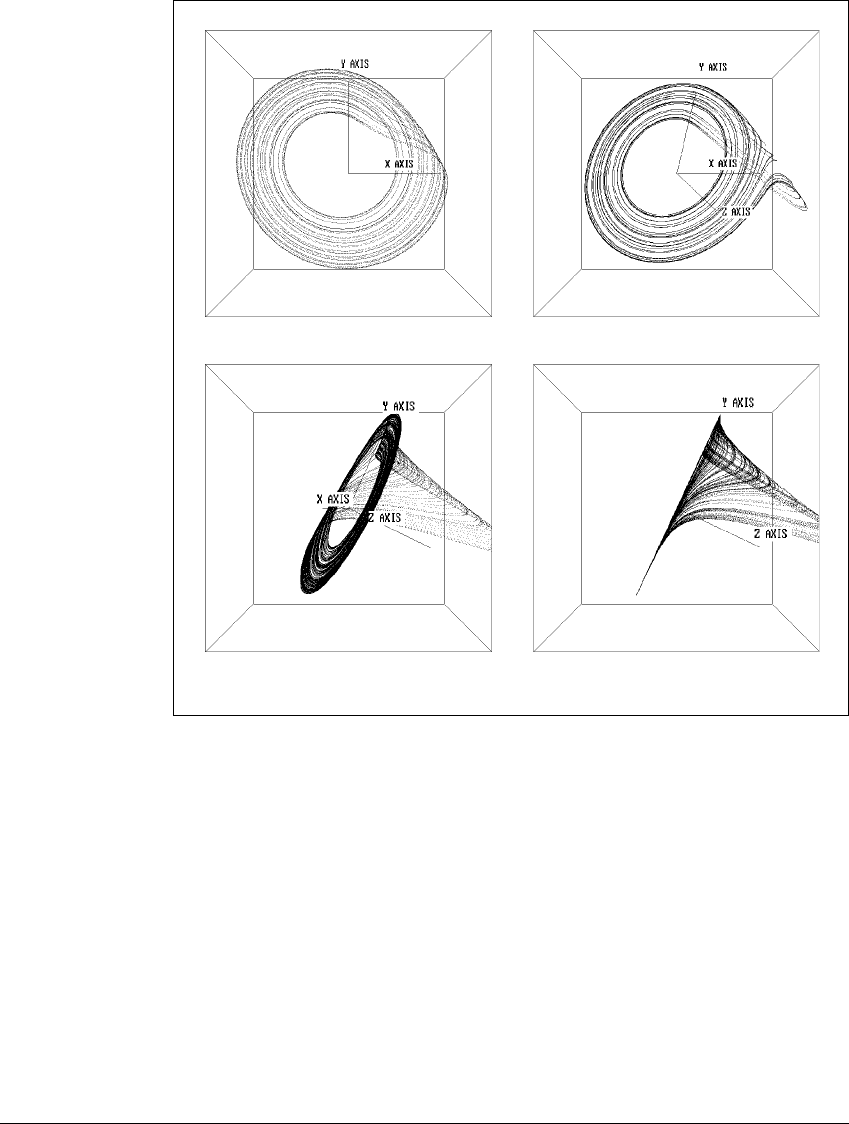
C HAOS IN D IFFERENTIAL E QUATIONS

(a) (b)

Figure 9.6 The R

ossler attractor.

Parameters are set at a ⫽ 0.1,b ⫽ 0.1, and c ⫽ 14. Four different views are shown.

The dynamics consists of a spiraling out from the inside along the xy-plane followed

by a large excursion in the z-direction, followed by re-insertion to the vicinity of

the xy-plane. Part (d) shows a side view. The Lyapunov dimension is 2.005—indeed

it looks like a surface.

inﬂuences between the x-andz-variable keep the orbit bounded. This motion is

shown in the four rotated views of the R

ossler attractor in Figure 9.6.

In Figure 9.7, we ﬁx a ⫽ b ⫽ 0.1, and vary the parameter c. For each c we

plot the attractor. A variety of different types of attractors can be seen, beginning

with a single loop periodic orbit, abruptly doubling its period when it turns into

a double loop at a bifurcation value of c, and then period-doubling twice more.

372

9.3 THE R

OSSLER ATTRACTOR

(a) c ⫽ 4, period 1 (b) c ⫽ 6, period 2 (c) c ⫽ 8.5, period 4

(d) c ⫽ 8.7, period 8 (e) c ⫽ 9, chaos (f) c ⫽ 12, period 3

(g) c ⫽ 12.8, period 6 (h) c ⫽ 13, chaos (i) c ⫽ 18, chaos

Figure 9.7 Attractors of the R

ossler system as

is varied.

Fixed parameters are a ⫽ b ⫽ 0.1. (a) c ⫽ 4, periodic orbit. (b) c ⫽ 6, period-

doubled orbit. (c) c ⫽ 8.5, period four. (d) c ⫽ 8.7, period 8. (e) c ⫽ 9, thin chaotic

attractor. (f) c ⫽ 12, period three. (g) c ⫽ 12. 8, period six. (h) c ⫽ 13, chaotic

attractor. (i) c ⫽ 18, ﬁlled-out chaotic attractor

The period-doublings continue inﬁnitely. This is another example of the period-

doubling route to chaos, which we have encountered previously in Figures 1.6 and

1.8 of Chapter 1 and Figure 2.16 of Chapter 2. We will study the period-doubling

bifurcation along with others in Chapter 11, and study period-doubling cascades

(inﬁnite sequences of doublings, of which this is an example) in Chapter 12.

373

C HAOS IN D IFFERENTIAL E QUATIONS

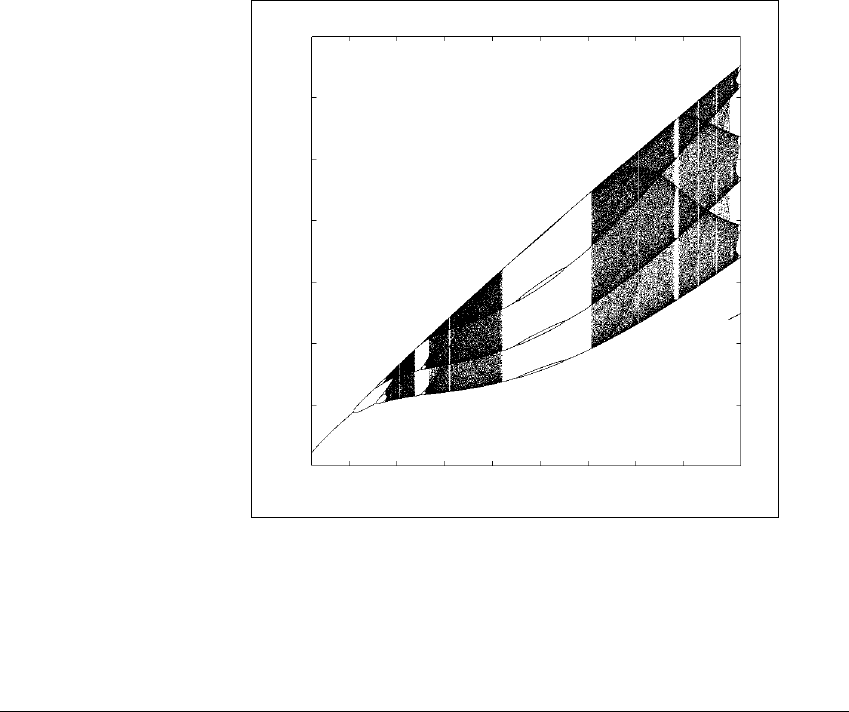
Figure 9.8 shows a bifurcation diagram for the R

ossler system. Again a

and b are ﬁxed at 0.1. For each c-value on the horizontal axis, we have plotted

the local maxima of the x-variable of the attracting solution. A single loop

(period one) orbit will have a single local maximum, and double loop (period

two) will typically have two separate local maxima, etc. We use period one

and period two in a schematic sense; the period-one orbit will have some ﬁxed

period T (not necessarily T ⫽ 1), and the so-called period-two orbit will have

period approximately double that of the period-one orbit. A chaotic attractor will

ordinarily have inﬁnitely many local maxima due to its fractal structure.

Starting at the left edge of Figure 9.8, we can see the existence of an

attracting period-one orbit which for larger c period-doubles into a period-two

orbit, which eventually period-doubles as well as part of a period-doubling cas-

cade. The result is a chaotic attractor, shown in Figure 9.7(e), followed by a

1 c 46

Figure 9.8 Bifurcation diagram for the R

ossler equations.

The parameters a ⫽ b ⫽ 0.1 are ﬁxed. The horizontal axis is the bifurcation pa-

rameter c. Each vertical slice shows a plot of the local maxima of the x-variable of

an attractor for a ﬁxed value of the parameter c. A single point implies there is a

periodic orbit; two points mean a periodic orbit with “two loops”, the result of a

period doubling, and so on. Near c ⫽ 46 the attractor disappears abruptly.

374

9.4 CHUA’ S C IRCUIT

period-three window, corresponding to Figure 9.7(f). The period-three orbit then

period-doubles as part of another period-doubling cascade. In the center of the

ﬁgure a period doubling of a period-four attractor is followed by a period-halving

bifurcation.

9.4 CHUA’S CIRCUIT

A rather simple electronic circuit became popular for the study of chaos dur-

ing the 1980’s (Matsumoto et al., 1985). It allows almost all of the dynamical

behavior seen in computer simulations to be implemented in an electronics lab

and viewed on an oscilloscope. As designed and popularized by L. Chua, an elec-

tronic engineering professor at the University of California at Berkeley, and the

Japanese scientist T. Matsumoto, it is an RLC circuit with four linear elements

(two capacitors, one resistor, and one inductor) and a nonlinear diode, which can

be modeled by a system of three differential equations. The equations for Chua’s

circuit are

x ⫽ c

(y ⫺ x ⫺ g(x))

y ⫽ c

(x ⫺ y ⫹ z)

z ⫽⫺c

y, (9.6)

where g(x) ⫽ m

x ⫹

⫺m

(|x ⫹ 1| ⫺ |x ⫺ 1|).

Another way to write g(x), which is perhaps more informative, is

g(x) ⫽











x ⫹ m

⫺ m

if x ⱕ⫺1

x if ⫺1 ⱕ x ⱕ 1

x ⫹ m

⫺ m

if 1 ⱕ x

(9.7)

The function g(x), whose three linear sections represent the three different

voltage-current regimes of the diode, is sketched in Figure 9.9. This piecewise

linear function is the only nonlinearity in the circuit and in the simulation equa-

tions. We will always use slope parameters satisfying m

⬍⫺1 ⬍ m

,asdrawnin

the ﬁgure.

Typical orbits for the Chua circuit equations are plotted in Figure 9.10. All

parameters except one are ﬁxed and c

is varied. Two periodic orbits are created

simultaneously in a Hopf bifurcation, which we will study in Chapter 11. They

begin a period-doubling cascade, as shown in Figure 9.10(b)-(c) and reach chaos

in Figure 9.10(d). The chaotic attractors ﬁll out and approach one another as c

is varied, eventually merging in a crisis, one of the topics of Chapter 10.

375

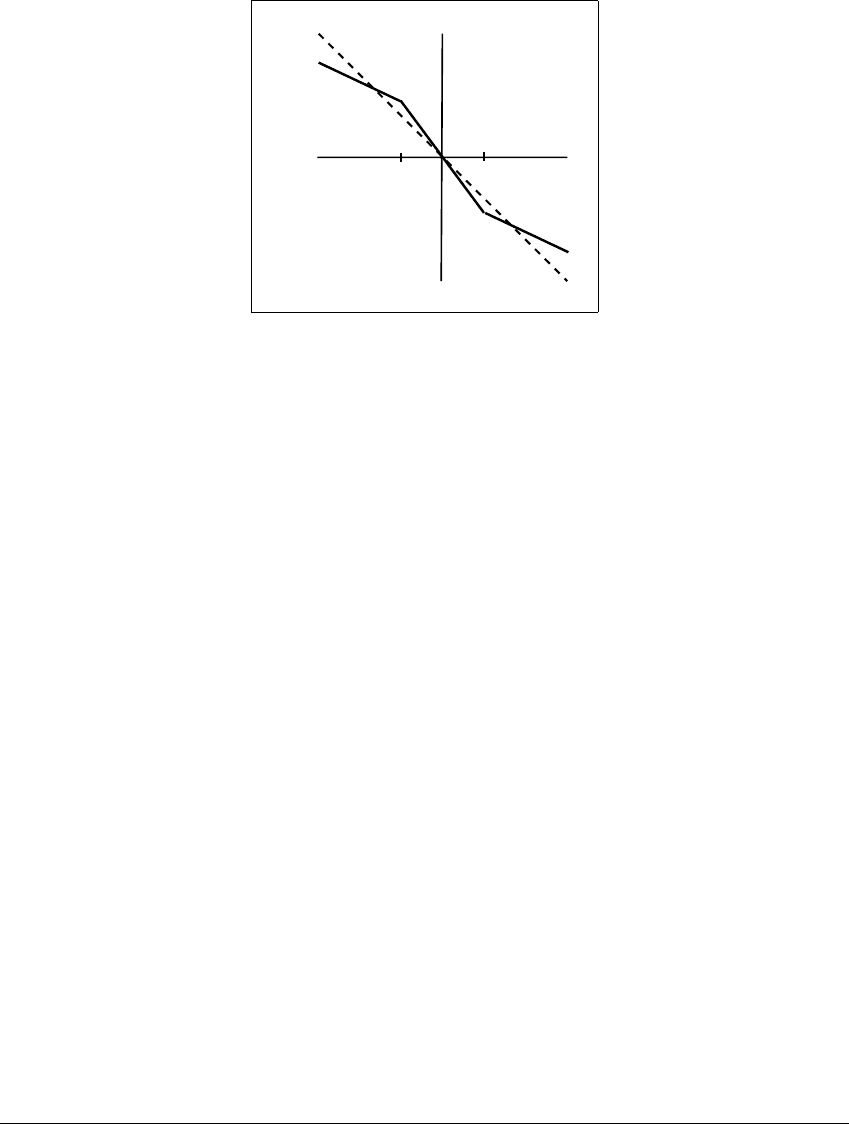
C HAOS IN D IFFERENTIAL E QUATIONS

1-1

y=g(x)

y=-x

Figure 9.9 The piecewise linear

(

) for the Chua circuit.

Equilibria correspond to intersections of the graph with the dotted line y ⫽⫺x.

Color Plate 17 shows a circuit diagram of Chua’s circuit. Color Plate 18

shows the computer-generated attractor for parameter settings c

⫽ 15.6, c

⫽ 1,

⫽ 25.58, m

⫽⫺8 7, m

⫽⫺5 7. Color Plate 19 shows a projection of the

experimental circuit attractor in the voltage-current plane, and Color Plate 20

shows an oscilloscope trace of the voltage time series.

9.5 FORCED OSCILLATORS

One way to produce chaos in a system of differential equations is to apply periodic

forcing to a nonlinear oscillator. We saw this ﬁrst for the pendulum equation in

Chapter 2. Adding damping and periodic forcing to the pendulum equation

␪

⫹ sin

␪

⫽ 0

produces

x ⫹ c

␪

⫹ sin

␪

⫽

␳

cos t,

which has apparently chaotic behavior for many parameter settings.

A second interesting example is the double-well Dufﬁng equation from

Chapter 7:

x ⫺ x ⫹ x

⫽ 0. (9.8)

376

9.5 FORCED O SCILLATORS

Figure 9.10 Chua circuit attracting sets.

Fixed parameters are c

⫽ 15.6, c

⫽ 1, m

⫽⫺8 7, m

⫽⫺5 7. The attracting

set changes as parameter c

changes. (a) c

⫽ 50, two periodic orbits. (b) c

⫽ 35,

the orbits have “period-doubled”. (c) c

⫽ 33.8, another doubling of the period.

(d) c

⫽ 33.6, a pair of chaotic attracting orbits. (e) c

⫽ 33, the chaotic attractors

fatten and move toward one another. (f) c

⫽ 25.58, a “double scroll” chaotic

attractor. This attractor is shown in color in Color Plate 18.

377