Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS IN D IFFERENTIAL E QUATIONS

Equation (9.8) describes motion under a potential energy ﬁeld which has minima

at x ⫽⫺1andx ⫽ 1. We can think of a ball rolling up and down the potential

wells of Figure 7.15(b). To model a ball that slowly loses energy because of friction,

we add a damping term:

x ⫹ c

x ⫺ x ⫹ x

⫽ 0. (9.9)

Most orbits of (9.9) end up in one or the other of the wells, no matter how much

energy the system begins with.

Both (9.8) and (9.9) are autonomous two-dimensional ﬁrst-order systems

in the variables x and

x, and as such their solution behavior falls under the

enforcement of the Poincar

e-Bendixson Theorem. For (9.8), most solutions are

periodic, either conﬁned to one well or rolling through both, depending on the

(constant) energy of the system. They are periodic orbits, which falls under case 2

of Theorem 8.8. If the system has total energy equal to 0, the peak between the two

wells in Figure 7.15(b), solutions will end up approaching the peak inﬁnitesimally

slowly (reaching the peak in “inﬁnite time”). The

␻

-limit set of these orbits is the

unstable equilibrium at the peak; this falls under case 1 of Theorem 8.8. For (9.9), a

solution can never reach a previous (x,

x) position because it would have the same

energy; but the energy is decreasing, as shown in Chapter 7. Therefore periodic

orbits are impossible, and each orbit converges to one of the three equilibrium

points, either the peak or one of the two well bottoms.

The forced damped double-well Dufﬁng equation

x ⫹ c

x ⫺ x ⫹ x

⫽

␳

sin t (9.10)

is capable of sustained chaotic motion. As a system in the two variables x and

x, it is nonautonomous; the derivative of y ⫽

x involves time. The usual trick is

to declare time as a third variable, yielding the autonomous three-dimensional

system

x ⫽ y

y ⫽⫺cy ⫹ x ⫺ x

⫹

␳

sin t

t ⫽ 1 (9.11)

Solutions of (9.10) are not bound by the Poincar

e-Bendixson Theorem.

The physical interpretation of the forced damped double-well Dufﬁng equa-

tion is fairly clear. The system, because of damping, is trying to settle in one of the

energy minima at the the bottom of the wells; due to the sinusoidal buffetting by

the forcing function, it cannot settle down. The bronze ribbon of Lab Visit 5 is a

378

9.6 LYAP U N OV E XPONENTS IN F LOWS

mechanical device that follows this behavior in a qualitative way. In the absence

of forcing, the magnet on the end of the ribbon will be trapped by one or the other

of the permanent magnets as it loses energy due to friction. When an alternating

magnetic ﬁeld is set up by turning on the coil, the ribbon oscillates aperiodically

for the duration of the experiment. The plot of (x,

x) in Lab Visit 5 is the time-2

␲

map of the experiment. It looks qualitatively similar to the time-2

␲

map of (9.10),

which is shown in Figure 9.11. Here we have set the forcing amplitude

␳

⫽ 3and

investigated two different settings for the damping parameter.

➮ COMPUTER EXPERIMENT 9.2

The attractors plotted in Figure 9.11 are sensitive to moderate-sized changes

in the parameters. Change the damping parameter c to 0.01 or 0.05 and explore

the attracting periodic behavior that results. Show parametric plots of the periodic

orbits in (x,

x) space as well as plots of the attractor of the time-2

␲

maps.

➮ COMPUTER EXPERIMENT 9.3

Plot orbits of the forced Van der Pol equation

x ⫹ c(x

⫺ 1)

x ⫹ x

⫽

␳

sin t.

Set parameters c ⫽ 0.1,

␳

⫽ 5 and use initial value (x,

x) ⫽ (0, 0) to plot an

attracting periodic orbit. What is its period? Repeat for

␳

⫽ 7; what is the new

period? Next ﬁnd out what lies in between at

␳

⫽ 6. Plot the time-2

␲

map.

9.6 LYAPUNOV EXPONENTS IN FLOWS

In this section, we extend the deﬁnition of Lyapunov exponents for maps, intro-

duced in Chapter 3, to the case of ﬂows. A chaotic orbit can then be deﬁned to

be a bounded aperiodic orbit that has at least one positive Lyapunov exponent.

First recall the concept of Lyapunov exponents for maps. The local behavior

of the dynamics varies among the many directions in state space. Nearby initial

conditions may be moving apart along one axis, and moving together along an-

other. For a given point, we imagined a sphere of initial conditions of inﬁnitesimal

radius evolving into an ellipse as the map is iterated. The average growth rate (per

iteration) of the longest orthogonal axis of the ellipse was deﬁned to be the ﬁrst

379

C HAOS IN D IFFERENTIAL E QUATIONS

⫺2

⫺2 x 2

(a)

⫺2

⫺2 x 2

(b)

Figure 9.11 Time-2

␲

map of the forced damped double-well Dufﬁng equation.

(a) The variables (x,

x) of (9.10) with c ⫽ 0.02,

␳

⫽ 3 are plotted each 2

␲

time units.

One million points are shown. (b) Same as (a), but c ⫽ 0.1. Compare with Figure

5.24, which was measured from experiment with a qualitatively similar system.

380

9.6 LYAP U N OV E XPONENTS IN F LOWS

Lyapunov number of the orbit, and its natural logarithm was called the Lyapunov

exponent. A positive Lyapunov exponent signiﬁes growth along that direction,

and therefore exponential divergence of nearby trajectories. The existence of a

local expanding direction along an orbit is the hallmark of a chaotic orbit.

For ﬂows, the concept is the same, once we replace the discrete iterations of

the map with the continuous ﬂow of a differential equation. Recall the deﬁnition

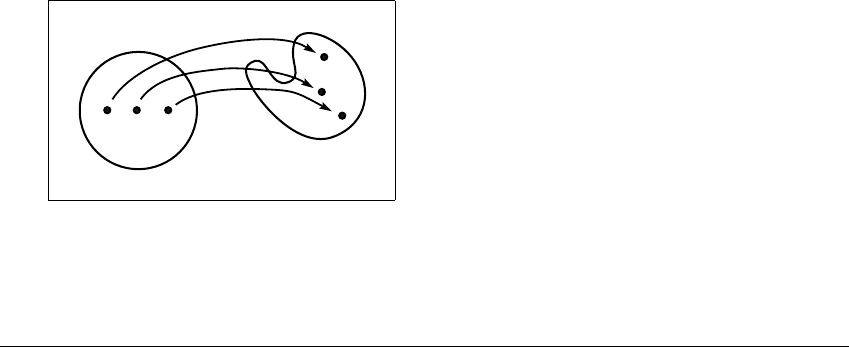
of the time-T map of a ﬂow F

(v). The ﬂow F

(v) is deﬁned to be the point at

which the orbit with initial condition v arrives after T time units.

Let

˙v ⫽ f(v) (9.12)

beasystemofn autonomous differential equations in v ⫽ (v

,...,v

). We deﬁne

the Lyapunov exponent of a ﬂow as the Lyapunov exponent of its time-T map for

T ⫽ 1.

Deﬁnition 9.2 The Lyapunov numbers (respectively, exponents)ofthe

ﬂow F

(v) are deﬁned to be the Lyapunov numbers (respectively, exponents) of

the associated time-1 map.

It is straightforward to deﬁne the time-T map F

, and to deﬁne the Lyapunov

numbers and exponents of a ﬂow, by simply falling back on our previous deﬁnitions

in the map case. We begin with a tiny sphere of initial conditions around some

, and imagine the evolution of the sphere as the initial conditions follow the

ﬂow of the differential equation. The only problem arises if you want to actually

determine the Lyapunov numbers and exponents. To do so, you will need to know

(v)

Figure 9.12 The time-T map

of a ﬂow.

A ball of initial conditions are followed from time t ⫽ 0totimet ⫽ T. The image

of the point v under F

is the position of the solution at time T of the initial value

problem with v

⫽ v.

381

C HAOS IN D IFFERENTIAL E QUATIONS

(v), the derivative of the the time-1 map F

(v) with respect to the initial

value v.

If we ﬁx T for the moment, DF

(v) is a linear map on ⺢

, represented by

an n ⫻ n matrix. Intuitively, the vector DF

(v)(w) is the small variation in the

solution of (9.12) at time T caused by a small change in the initial value at t ⫽ 0

from v to v ⫹ w.

Although there is no explicit formula for the matrix DF

(v), we can ﬁnd a

differential equation involving it that can be solved in parallel with (9.12). Since

兵F

(v):t in ⺢其 is the solution of (9.12) with initial value v,wehavebydeﬁnition

(v) ⫽ f(F

(v)). (9.13)

This equation has two variables, time t and the initial value v in ⺢

. Differentiating

with respect to v, the chain rule yields

(v) ⫽ Df(F

(v)) ⭈ DF

(v), (9.14)

which is known as the variational equation of the differential equation. The

name comes from the fact that if we could solve the equation for DF

(v), we

would know the derivative matrix of F

, and therefore know how F

acts under

small variations in the initial value v.

To simplify the looks of the variational equation, deﬁne

⫽ DF

(v)

to be the Jacobian of the time-t map evaluated at initial value v,and

A(t) ⫽ Df(F

(v))

to be the matrix of partial derivatives of the right-hand side f of the differential

equation (9.12) evaluated along the solution. Note that A(t) can be computed

explicitly from knowledge of the original differential equation. Then we can

rewrite the variational equation (9.14) as

⫽ A(t)J

. (9.15)

In writing (9.14) this way, we have ﬁxed v, the initial value of the orbit under

consideration, and so have not explicitly written it into (9.15). In order to

uniquely deﬁne J

from (9.15), we need to add an initial condition, which is J

⫽ I,

the identity matrix. This follows from the fact that the ﬂow satisﬁes F

(v) ⫽ v by

deﬁnition. The variational equation (9.15) is a linear differential equation, even

382

9.6 LYAP U N OV E XPONENTS IN F LOWS

when the original differential equation has nonlinear terms. Unlike the original

equation (9.12), it is not autonomous, since A(t) is time-dependent in general.

E XAMPLE 9.3

In order to calculate the output of the time-T map F

(v) for the Lorenz

equations, it sufﬁces to solve the equations with initial condition v

⫽ (x

)

and to follow the trajectory to time T;then

) ⫽ (x(T),y(T),z(T)).

Next we show how to calculate the 3 ⫻ 3 Jacobian matrix J

of the three-

dimensional map F

. Differentiating the right-hand-side of the Lorenz equations

(9.1) yields

A(t) ⫽







⫺

␴␴

r ⫺ z(t) ⫺1 ⫺x(t)

y(t) x(t) ⫺b







. (9.16)

Each column of J

can be calculated individually from the variational equation

(9.15). For example, the ﬁrst column of J

is the solution of the differential

equation







(t)







⫽ A(t)







(t)







(9.17)

at time T, and the other two columns satisfy a similar equation. Notice that the

current A(t) needs to be available, which involves the current (x(t),y(t),z(t)).

So the variational equation must be solved simultaneously with a solution of the

original differential equation (9.12).

An important fact about the Jacobian matrix J

⫽ DF

(v)ofthetime-T

map evaluated at v is that it maps small variations tangent to the orbit at time 0

to small variations tangent to the orbit at time T. More precisely,

(v) ⭈ f(v) ⫽ f(F

(v)). (9.18)

As usual, v denotes the initial value of the ﬂow at time 0, and F

(v) the value at

time T.Sincef is the right-hand-side of the differential equation, it deﬁnes the

direction of the orbit at each time.

383

C HAOS IN D IFFERENTIAL E QUATIONS

The derivation of this fact follows from applying the variational equation

(9.14) to the vector f(v):

(v)f(v) ⫽ Df(F

(v)) ⭈ DF

(v)f(v). (9.19)

Setting w ⫽ DF

(v)f(v), we see that w(t) satisﬁes the initial value problem

˙w ⫽ Df(F

(v))w

w(0) ⫽ f(v). (9.20)

On the other hand, differentiating the original equation (9.13) with respect to t

yields

(v) ⫽ Df(F

(v))

(v)

f(F

(v)) ⫽ Df(F

(v))f(F

(v)), (9.21)

and f(F

(v)) equals f(v) at time 0. Since w and f(F

(v)) satisfy the same initial

value problem, they are equal.

The important consequence of (9.18) is that a bounded orbit of an au-

tonomous ﬂow (9.12) either has one Lyapunov exponent equal to zero, or

else it has an equilibrium in its

␻

-limit set. If the latter does not occur, then

0 ⬍ b ⬍ |f(F

(v))| ⬍ B for all t, for some positive bounds b and B.Ifr(n)isthe

expansion in the direction of f(v)aftern time units (n steps of the time-1 map),

then

0 ⱕ lim

n→

⬁

ln b ⱕ lim

n→

⬁

ln r(n) ⱕ lim

n→

⬁

ln(B) ⱕ 0.

Therefore the Lyapunov exponent in the direction tangent to the orbit is zero.

The change in volume due to the ﬂow can be found with the help of

a famous formula due to Liouville. Deﬁne ⌬(t) ⫽ det J

where

⫽ A(t)J

as in

(9.15). Liouville’s Formula (Hartman, 1964) says that ⌬(t) satisﬁes the differential

equation and initial condition

⌬



⫽ Tr( A(t))⌬

⌬

⫽ det J

⫽ 1, (9.22)

where Tr denotes the trace of the matrix A(t). It follows directly from (9.22) that

det J

⫽ exp





Tr A(t) dt



. (9.23)

384

9.6 LYAP U N OV E XPONENTS IN F LOWS

Deﬁnition 9.4 A system of differential equations is dissipative if its time-

T map decreases volume for all T ⬎ 0.

Note that Tr(A(t)) ⬍ 0 for all t implies that the system is dissipative. For

the Lorenz equations, Tr A(t) ⫽⫺(

␴

⫹ 1 ⫹ b), so that

det J

⫽ e

⫺(

␴

⫹1⫹b)t

The volume decrease is constant for all v. In one time unit, a ball of initial

conditions decreases in volume by a factor of e

⫺(

␴

⫹1⫹b)

. For the standard Lorenz

parameters

␴

⫽ 10 and b ⫽ 8 3, this factor is 0.00000116 per second, so it is a

dissipative system.

E XAMPLE 9.5

(Forced damped pendulum.) Liouville’s formula can also be used to ﬁnd

the area contraction rate for the time-2

␲

map of the forced damped pendulum,

a dissipative system introduced in Chapter 2. First, write the equation

x ⫹ c

x ⫹

sin x ⫽ b cos t in the form of a ﬁrst-order system:

x ⫽ y

y ⫽⫺cy ⫺ sin x ⫹ b cos t

t ⫽ 1. (9.24)

Then

A(t) ⫽







010

⫺ cos x ⫺c ⫺b sin t

000







. (9.25)

Equation (9.23) shows us that the area contraction rate per iteration of the

time-2

␲

map is

exp





␲

Tr A(t) dt



⫽ exp





␲

⫺cdt



⫽ e

⫺2

␲

. (9.26)

With the deﬁnition of Lyapunov exponent in hand, we can go on and deﬁne

chaotic orbit in a straightforward way.

Deﬁnition 9.6 Let F

) be a solution of ˙v ⫽ f(v), where v

僆⺢

. We

say the orbit F

)ischaotic if the following conditions hold:

385

C HAOS IN D IFFERENTIAL E QUATIONS

1. F

),tⱖ 0, is bounded;

2. F

) has at least one positive Lyapunov exponent; and

␻

) is not periodic and does not consist solely of equilibrium points,

or solely of equilibrium points and connecting arcs (as in the conclusion

of the Poincar

e–Bendixson Theorem).

In order to be precise, one might also rule out higher-dimensional

␻

-limit

sets on which the map exhibits some sort of patterned behavior, such as the

example of the irrational ﬂow on the torus in Chapter 8. If the torus itself is

repelling in ⺢

, then a well-behaved dense orbit on the torus can have a positive

Lyapunov exponent, but we would not want to consider it a chaotic orbit.

386

C HALLENGE 9

☞ C HALLENGE 9

Synchronization of Chaotic Orbits

SURPRISING FACT about chaotic attractors is their susceptibility to syn-

chronization. This refers to the tendency of two or more systems which are coupled

together to undergo closely related motions, even when the motions are chaotic.

There are many types of synchronization, depending on whether the mo-

tions are identical or just related in some patterned way. Synchronization can be

local, meaning that the synchronized state is stable, and that once synchronized,

small perturbations will not desynchronize the systems; or global, meaning that

no matter where the systems are started in relation to one another, they will

synchronize. There are also different ways to couple the systems. Coupling can be

one-way, in which outputs from one system affect the second system but not vice

versa, or two-way, in which each affects the other.

In Challenge 9, you will ﬁrst establish a theorem that explains local syn-

chronization for two-way coupled identical nonlinear systems. It states that if

the coupling is strong enough, then identical systems which are started close

enough together will stay close forever. Secondly, there is an example of global

synchronization for one-way coupling, in which two identical Lorenz systems,

started with arbitrary different initial conditions, will synchronize exactly: their

(x, y, z) states are eventually (asymptotically) equal as a function of time. Both

of these behaviors are different from the behavior of identical uncoupled (that is,

independent) chaotic systems. If the latter are started with approximately equal

but nonidentical initial conditions, we know that sensitive dependence will cause

the two systems to eventually move far apart.

Here is synchronization in its simplest form. Consider the two-way coupled

system of autonomous differential equations

x ⫽ ax ⫹ c(y ⫺ x)

y ⫽ ay ⫹ c(x ⫺ y). (9.27)

Assume that a ⬎ 0. We consider the original identical systems to be

x ⫽ ax and

y ⫽ ay. The coupling coefﬁcient c measures how much of x to replace with y in

the x-equation, and the reverse in the y-equation. First notice that if the coupling

is turned off, there is no synchronization. The solutions for c ⫽ 0arex(t) ⫽ x

and y(t) ⫽ y

, and the difference between them is |x(t) ⫺ y(t)| ⫽ |x

⫺ y

which increases as a function of time because of our assumption a ⬎ 0. In this

387