Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS IN D IFFERENTIAL E QUATIONS

case the synchronized state x(t) ⫽ y(t) is unstable: if x

⫽ y

, any small difference

caused by perturbing the systems will grow exponentially.

As we turn on the coupling, at ﬁrst we see little difference from the uncou-

pled case. Figure 9.13(a) shows plots of x(t)andy(t) for a ⫽ 0.1 and coupling

parameter c ⫽ 0.03. The difference between the two trajectories, started from

two different initial values, again grows exponentially. Figure 9.13(b) is the result

of stronger coupling c ⫽ 0.07. The trajectories move towards one another and

stay together as t increases. This is an example of global synchronization. Your

ﬁrst assignment is to ﬁnd the mechanism that explains the difference between

the two cases.

Step 1 Write (9.27) as the linear system





⫽ A





where A ⫽



a ⫺ cc

ca⫺ c



. (9.28)

Find the eigenvalues and eigenvectors of A.Deﬁneu ⫽ S

⫺1





,whereS is

the matrix whose columns are the eigenvectors of A. Write down and solve the

corresponding differential equation for u.

Step 2 Using Step 1, ﬁnd the solution of system (9.27). Show that |x(t) ⫺

y(t)| ⫽ |x

⫺ y

(a⫺2c)t

t t

(a) (b)

Figure 9.13 Synchronization of scalar trajectories.

(a) Two solutions of the coupled system (9.27) with a ⫽ 0.1 and weak coupling

c ⫽ 0.03. Initial values are 5 and ⫺4.5. The distance between solutions increases

with time. (b) Same as (a), but with stronger coupling c ⫽ 0.07. The solutions

approach synchronization.

388

C HALLENGE 9

Step 2 explains the difference between the weak coupling in Figure 9.13(a)

and stronger coupling in Figure 9.13(b). The coupling parameter must be greater

than a 2 to cause the two solutions to synchronize.

Now that we see how to synchronize coupled scalar equations, let’s consider

coupled linear systems. Let A be an n ⫻ n matrix. Deﬁne the linear system

˙v ⫽ Av (9.29)

and the coupled pair of linear systems

˙v

⫽ Av

⫹ c(v

⫺ v

)

˙v

⫽ Av

⫹ c(v

⫺ v

)

which can be rewritten as



˙v



⫽



A ⫺ cI cI

cI A ⫺ cI





. (9.30)

Step 3 Show that if v is an eigenvector of A,thenboth(v

, v

)

⫽ (v, v)

and (v, ⫺v)

are eigenvectors of the matrix in (9.30). Denote the eigenval-

ues of A by

␭

,...,

␭

. Show that the eigenvalues of the matrix in (9.30) are

␭

,...,

␭

⫺ 2c,...,

␭

⫺ 2c.

Step 4 Deﬁne the difference vector u ⫽ v

⫺ v

. Show that u satisﬁes the

differential equation

˙u ⫽ (A ⫺ 2cI)u. (9.31)

Step 5 Show that if all eigenvalues of A have real part less than 2c,then

the origin of (9.31) is globally asymptotically stable (see Chapter 7). Conclude

that for sufﬁciently large coupling, the solutions v

(t)andv

(t) of (9.29) undergo

global synchronization, or in other words, that for any initial values v

(0) and

(0),

lim

t→

⬁

(t) ⫺ v

(t)| ⫽ 0.

When the equilibrium u ⫽ v

⫺ v

⫽ 0 is globally asymptotically stable,

we say that the system undergoes global synchronization. If instead u ⫽ 0 is only

stable, we use the term local synchronization.

Now we move on to nonlinear differential equations. Consider a general

autonomous system

˙v ⫽ f(v) (9.32)

389

C HAOS IN D IFFERENTIAL E QUATIONS

and the coupled pair of systems

˙v

⫽ f(v

) ⫹ c(v

⫺ v

)

˙v

⫽ f(v

) ⫹ c(v

⫺ v

) (9.33)

The variational equations for a synchronized trajectory of (9.33) are



˙v



⫽



A(t) ⫺ cI cI

cI A(t) ⫺ cI





, (9.34)

where A(t) ⫽ D

f(v

(t)) is the matrix of partial derivatives of f evaluated along

the synchronized trajectory v

(t) ⫽ v

(t). To determine whether this trajectory

is stable, we will investigate u ⫽ v

⫺ v

.LetJ(t) denote the Jacobian matrix of

the time-t map of the ﬂow of v of (9.32), and K(t) denote the Jacobian matrix of

the time-t map of the ﬂow of u.

Step 6 Show that J



(t) ⫽ A(t)J(t)andK



(t) ⫽ (A(t) ⫺ 2cI)K(t). Using

initial conditions J(0) ⫽ K(0) ⫽ I, show that K(t) ⫽ J(t)e

⫺2ct

Step 6 shows the relationship between the matrix J(1), the Jacobian deriva-

tive of the time-1 map for the original system, and the matrix K(1), the derivative

of the time-1 map of the difference vector u.

Step 7 Prove:

Theorem 9.7 (Synchronization Theorem.) Let

␭

be the largest Lyapunov

exponent of the system (9.32). Assume two-way coupling as in (9.33).Ifc⬎

␭

 2,

then the coupled system satisﬁes local synchronization. That is, the synchronized state

u(t) ⫽ v

(t) ⫺ v

(t) ⫽ 0 is a stable equilibrium.

Figure 9.14 shows an application of the Synchronization Theorem. For the

Chua circuit which generates the double scroll attractor of Figure 9.10(f), the x-

coordinate oscillates between negative and positive values. The largest Lyapunov

exponent of the chaotic orbit is approximately

␭

⫽ 0.48.

Figure 9.14(a) shows the x-coordinates plotted from a coupled pair of Chua

circuit systems as in (9.32) with c ⫽ 0.15. The initial values used were (0, 0.3, 0)

for v

and (⫺0.1, 0.3, 0) for v

. Although the trajectories begin very close to-

gether, they soon diverge and stay apart. Part (c) of the Figure shows a scatter

plot of the simultaneous x-coordinates of v

and v

. It starts out by lying along

the identity diagonal, but eventually roams around the square. The lack of syn-

chronization is expected because of the weak coupling strength. In part (b) of

the Figure, the coupling parameter is c ⫽ 0.3 ⬎

␭

 2, and synchronization is

observed.

390

C HALLENGE 9

t t

(a) (b)

-3

-3 0 3

x-coordinate of v2

x-coordinate of v1

-3

-3 0 3

x-coordinate of v2

x-coordinate of v1

Figure 9.14 Synchronization of the Chua attractor.

(a) Time traces of the x-coordinates of v

(solid) and v

(dashed) for coupling

strength c ⫽ 0.15. (b) Same as (a), but for c ⫽ 0.30. (c) A simultaneous plot of one

curve from (a) versus the other shows a lack of synchronization. (d) Same as (c),

but using the two curves from (b). The plot lines up along the diagonal since the

trajectories are synchronized.

One-way coupling can also lead to synchronization. Next we write a pair of

Lorenz systems. The ﬁrst is to be considered the sender:

⫽⫺

␴

⫹

␴

⫽⫺x

⫹ rx

⫺ y

(9.35)

⫽ x

⫺ bz

and the second the receiver:

⫽⫺

␴

⫹

␴

⫽⫺x

⫹ rx

⫺ y

(9.36)

⫽ x

⫺ bz

391

C HAOS IN D IFFERENTIAL E QUATIONS

Notice that the receiver contains a signal x

from the sender, but that the sender

is autonomous. Using the Lyapunov function ideas from Chapter 7, you will show

how to guarantee that the difference vector u ⫽ (u

) ⫽ (y

⫺ y

⫺ z

)

tends to 0 for any set of initial conditions.

Step 8 Assume that b ⬎ 0. Show that the function E(u

) ⫽ u

⫹ u

is a strict Lyapunov function for the synchronized state u ⫽ 0. Conclude that

the receiver trajectory (x

) globally synchronizes to the sender trajectory

Postscript. Since the discovery of one-way coupling results like Step 8 by (Pecora

and Carroll, 1990), there has been engineering interest in the use of the synchronization

of chaos for the purpose of communications. The R

ossler and Chua attractors have also

been shown to admit global synchronization by one-way coupling.

Various schemes have been suggested in which the signal transmitted by the sender

can be used as a message carrier. For example, very small intermittent perturbations

(perhaps a secret message m coded in binary numbers) could be added to the signal x

and sent to the receiver. Since the signal plus message is mostly chaos, reading the message

would presumably be difﬁcult. However, if the receiver could synchronize with the sender,

its x

would be equal to x

with the perturbations m greatly reduced (since they are small

compared to x

, the receiver acts as a type of ﬁltering process). Then the receiver could

simply subtract its reconstructed x

from the received x

⫹ m to recover m,thecoded

message. For more details on this and similar approaches, see the series of articles in

Chapter 15, Synchronism and Communication, of (Ott, Sauer, and Yorke, 1994).

392

E XERCISES

9.1. Find out what happens to trajectories of the Lorenz equations (9.1) whose initial

conditions lie on the z-axis.

9.2. Find all equilibrium points of the Chua circuit system (9.6). Show that there are

three if m

⬍⫺1 ⬍ m

, and inﬁnitely many if m

⫽⫺1.

9.3. Find the area-contraction rate per iteration of the time-2

␲

map of the forced damped

double-well Dufﬁng equation (9.10). For what values of damping parameter c is it

dissipative?

9.4. Find a formula for the area-contraction rate per iteration of the time-1 map of the

linear system ˙v ⫽ Av,whereA is an n ⫻ n matrix.

9.5. Damped motion in a potential ﬁeld is modeled by

x ⫹ c

x ⫹

⳵

⫽ 0, as in (7.41).

Use (9.23) to prove that the sum of the two Lyapunov exponents of any orbit in the

(x,

x)-plane is ⫺c.

9.6. Find the Lyapunov exponents of any periodic orbit of undamped motion in a potential

ﬁeld, modeled by

x ⫹

⳵

⫽ 0.

9.7. How are the Lyapunov exponents of an orbit of the differential equation ˙v ⫽ f(v)

related to the Lyapunov exponents of the corresponding orbit of ˙v ⫽ cf(v), for a

constant c?

9.8. Show that if an orbit of (9.12) converges to a periodic orbit, then they share the

same Lyapunov exponents, if they both exist.

9.9. Consider the unforced, undamped pendulum equation

x ⫹ sin x ⫽ 0.

(a) Write as a ﬁrst-order system in x and y ⫽

x, and ﬁnd the variational

equation along the equilibrium solution (x, y) ⫽ (0, 0).

(b) Find the Jacobian J

of the time-1 map at (0,0), and ﬁnd the Lyapunov

exponents of the equilibrium solution (0,0).

␲

, 0).

(d) Repeat (b) for the equilibrium solution (x, y) ⫽ (

␲

, 0).

(e) Find the Lyapunov exponents of each bounded orbit of the pendulum.

393

C HAOS IN D IFFERENTIAL E QUATIONS

☞ L AB V ISIT 9

Lasers in Synchronization

HE EQUATIONS governing the output of a laser are nonlinear. There is a

large amount of interest in the ﬁeld of nonlinear optics, in which researchers

study laser dynamics and related problems. The natural operating state of a laser

consists of very fast periodic oscillations. During the last 20 years, it has become

relatively straightforward to design a laser that operates in a chaotic state.

In his lab at the Georgia Institute of Technology, R. Roy and coworkers

have studied many aspects of the nonlinear dynamics of Nd:YAG lasers. (The

acronym stands for neodymium-doped yttrium aluminum garnet.) The intensity

of the laser ﬂuctuates, making a complete oscillation in several microseconds (1

microsecond ⫽ 10

⫺6

seconds). Depending on parameter settings, the pattern of

oscillations can be either periodic or chaotic. Systems of nonlinear differential

equations exist that do a very precise job of modeling the instantaneous electric

and magnetic ﬁeld and population inversion of the laser. (See (Haken, 1983) for

example.)

In this synchronization experiment, two Nd:YAG lasers exhibiting chaotic

intensity ﬂuctuations are placed side by side on a lab table. The two laser beams

are coupled through overlap of their electromagnetic ﬁelds, which ﬂuctuate with

time. The width of each beam is much less than a millimeter. The closer the two

beams, the stronger the mutual couplings of their respective differential equations.

In units relevant to the experiment, the mutual coupling strength is ⬇ 10

⫺2

when

the beam separation is 0.6mmand⬇ 10

⫺12

when the separation is 1.5 mm.

Figure 9.15 shows a diagram of the pair of pumped lasers. The two beams are

driven by a single argon laser, shown at left. Beam-splitters and mirrors divide the

argon laser beam into two beams, each of which lases in the Nd:YAG crystal. The

two beams lase far enough apart that the population inversions of the two lasers do

not overlap—the coupling occurs only through the overlap of the electromagnetic

ﬁelds of the beams.

The beam separation can be changed using the beam combiner, marked BC

in Figure 9.15. The two separate laser beams are marked with a single arrow and

Roy, R., and Thornburg, K.S. 1994. Experimental synchronization of chaotic lasers.

Physical Review Letters 72:2009–2012.

394

L AB V ISIT 9

Figure 9.15 Diagram of two spatially-coupled lasers.

The two beams, denoted by a single arrow and double arrows, are driven periodically

by the same argon laser at left. The separation distance is controlled by BC, the

beam combiner. Lasing of the two beams takes place in the crystal, and output

intensity is measured at the photodiodes PD1 and PD2.

double arrows, respectively. The laser output intensity is measured by the video

camera and the photodiodes PD1 and PD2, which feed an oscilloscope for data

recording.

The chaos in the laser beam is caused by making the argon laser output

oscillate periodically. This is achieved by putting the argon laser beam through the

acousto-optic modulator, denoted AOM. When the AOM is placed in position

(a), only one beam is chaotic; in position (b), both beams are chaotic. For large

separations of the beams within the crystal, say d ⫽ 1.5 mm, the two lasers operate

independently and are unsynchronized.

For smaller separations (d ⬍ 1 mm), the effects of synchronization begin

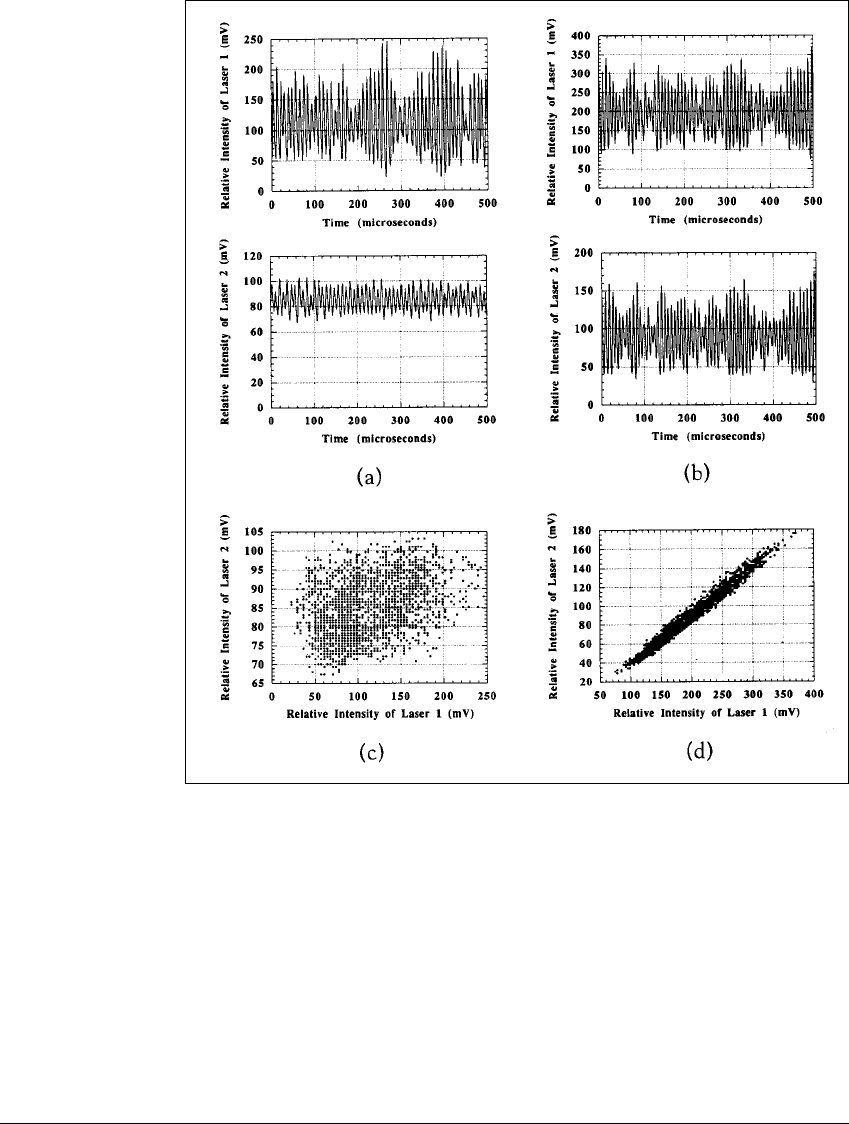
to appear. Figure 9.16(a) shows the intensity as a function of time for the two

beams, for d ⫽ 1 mm. Although the two beams are not synchronized, the weak

coupling with laser 1 causes the previously quiet laser 2 to ﬂuctuate in an erratic

fashion. Figure 9.16(c) plots simultaneous intensities versus one another. The

wide scattering of this plot shows that no synchronization is occurring. This

395

C HAOS IN D IFFERENTIAL E QUATIONS

Figure 9.16 Synchronization of intensities for two coupled lasers.

(a) The beams are separated by d ⫽ 1 mm. Laser 1 is chaotic, as shown by the

time trace of its intensity. The coupling has caused Laser 2, which is nominally

at equilibrium, to oscillate erratically. The coupling is not strong enough to cause

synchronization. (b) The beam separation is reduced to d ⫽ 0.75 mm, causing

signiﬁcant interaction of the two electromagnetic ﬁelds. Laser 1 is chaotic as before,

but now the mutual coupling has caused Laser 2 to oscillate in synchronization with

Laser 1. (c) At each time, the intensities of lasers 1 and 2 in (a) are plotted as an

xy-point. The lack of pattern shows that there is no synchronization between the

two beams at the weak coupling strength. (d) The xy-plot from (b) lies along the

line y ⫽ x, verifying synchronicity.

396

L AB V ISIT 9

ﬁgure can be compared with the similar Figure 9.14, which shows analogous

behavior with the Chua circuit.

In Figure 9.16(b), the beam separation has been decreased to d ⫽ 0.75 mm.

The intensities are now in synchronization, as shown by the match of the time

traces as well as the fact that the scatter plot is restricted to the diagonal. In both

the weak and strong coupling cases in Figure 9.16, the AOM was in position (a),

although similar behavior is found for position (b).

Besides possible uses of synchronization in communication applications, as

suggested in Challenge 9, there are many other engineering possibilities. For ad-

vances in electronics that rely on the design of devices that harness large numbers

of extremely small oscillators, split-second timing is critical. Synchronization of

chaos may lead to simple ways to make subunits operate in lockstep.

397