Ammari H., Benkirane A., Touzani A. (editors) Recent Developments in Nonlinear Analysis

Подождите немного. Документ загружается.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

290

Floquet states of periodically time-dependent harmonic

oscillators

Y. Achkar, S. Sayouri, and A. L. Marrakchi

Laboratoire de Physique Th´eorique et Appliqu´ee (LPTA)

D´epartement de Physique

Facult´e des Sciences Dhar-Mehraz

B.P. 1796, F´es-Atlas, F´es, Morocco

Floquet theory together with the resonating averages method (RAM) were used

to solve the Schr¨odinger equation of periodically-time-dependent harmonic os-

cillators. The approach gives another way of solving this equation, and lead

to identical analytical solutions to those published in the literature based on

diﬀerent other methods.

Keywords: Time-dependent harmonic oscillator; Floquet operators; Floquet

states; Jump operators; Resonating averages method; Uncertainty relation.

1. Introduction

Numerous physical and mathematical studies have been devoted to the

construction of consistent formalism of explicitly time-dependent quantum

systems

Among these quantum systems, the time-dependent harmonic

oscillator has attracted considerable interest in the past few decades

1218

not only because it is a system that can be exactly solved and is con-

sidered as a great pedagogical tool, but also because it is a very relevant

system and possessing many applications in diﬀerent areas of physics: quan-

tum optics, plasma physics, quantum ﬁeld theory, gravitation, cosmology,

etc.

The harmonic oscillator with a time-dependent mass and a constant fre-

quency has been the subject of many researches

1921

Abdalla et al.

have studied this system in order to describe the electromagnetic ﬁeld in-

tensities in a Fabry-Perot cavity. The harmonic oscillator with a constant

mass and a time-dependent frequency was used by Lemos et al.

in a the-

oretical approach of the expansion of the universe and by Paul

for the

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

291

discovery of electromagnetic traps for charged and neutral particles (known

as Paul-traps). In previous work,

we have introduced a direct theoretical

approach for solving the equations of motion of the time-dependent har-

monic oscillator, in Heisenberg picture, with some direct applications.

The purpose of this paper is to solve the Schr¨odinger evolution equation

of periodically-time-dependent harmonic oscillator. We have established a

theoretical approach based on the Floquet theory

combined with the res-

onating averages method elaborated by Lochak and Thiounn.

Hence,by

using the Floquet decomposition operators and developing the evolution

operator with the help of the resonating averages method from ﬁrst order

to second ameliorated order, we have determinate the Floquet operators,

and Floquet states. Moreover, we have proposed a theoretical form of jump

operators between the instantaneous Floquet states, and veriﬁed the un-

certainty principle.

This paper is organized as follows: in the ﬁrst part, we present the the-

oretical formalism of the purposed approach. In the second part, we apply

the method for the forced harmonic oscillator, the harmonic oscillator with

a time-dependent mass and a constant frequency, the harmonic oscillator

with a constant mass and a time-dependent frequency, and the harmonic

oscillator with a time-dependent mass and frequency. Some direct compar-

isons of our results with some published works are given,

1218

2. Formalism

We consider a quantum system described by a time-dependent Hamiltonian

such as

H(t) = H

+ µH

(t) (1)

where H

is the Hamiltonian of the unperturbed oscillator, and H

(t) the

Hamiltonian of perturbation with amplitude µ.

2.1. Floquet approach

In the case of periodically time-varying Hamiltonian, the Floquet theorem

asserts the existence of an operator V (t), a fundamental solution of the

well-known Schr¨odinger evolution equation, in the form

V (t) = T (t)e

−iRt/~

(2)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

292

Where T (t) is a periodic unitary operator of the same period as H

(t), and

R is a constant hermitian operator. The time-evolution operator can be

written as

U(t, t

) = V (t)V

−1

) (3)

in the interaction picture it satisﬁes the following diﬀerential equation

(t, t

)

= µH

(t)U

(t, t

) (4)

where

(t) = e

t/~

(5)

According to the Floquet theorem, the Floquet states, solutions of the

Schr¨odinger equation, are deﬁned as

|ψ

(t)i = T (t)|φ

(t)i (6)

where |φ

(t)i are the eigenstates of R, with the eigenvalues ε

, such as

d|Φ

(t)i

= R|Φ

(t)i (7)

and

|φ

(t)i = e

−iε

t/~

|ni (8)

|ni are the number states of the unperturbed system.

We notice that the fundamental propriety of those Floquet states is the

fact that they form a complet set of time-dependent solutions in the Hilbert

space. So, the global state |Ψ(t)i of the quantum system can be written in

the form of a linear combination of the |Ψ

(t)i :

|Ψ(t)i =

|Ψ

(t)i

where the a

are time-independent coeﬃcients.

2.2. Jump operators

We introduce the operators A(t) and A

(t) which are responsible for the

instantaneous transitions between the Floquet states. Their eﬀects on the

Floquet states are similar to those of the conventional annihilation and

creation operators. These operators must satisfy the conditions

A(t)|ψ

(t)i =

√

n|ψ

n−1

(t)i (9)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

293

(t)|ψ

(t)i =

√

n + 1|ψ

n+1

(t)i (10)

So, their expressions are deﬁned by the relations

A(t) = e

∆ε

T (t)aT

(t) (11)

(t) = e

−i

∆ε

T (t)a

(t) (12)

where ∆ε is the diﬀerence between two successive Floquet levels:

∆ε = ε

n+1

− ε

(13)

The Floquet decomposition (Eq. (2)) gives us diﬀerent possibilities to solve

the evolution equation of the periodically-time-dependent harmonic oscil-

lator. However, the determination of the corresponding Floquet operators

is not unique, while the Floquet theory supposes the existence of an inﬁ-

nite number of couples (R, T (t)), solutions of equation (2), depending on

the form of the perturbed Hamiltonian. To determine these two operators,

we used the technique of the resonating averages method elaborated by

G.Lochak,

based on the generalized Bogoliubov approximation.

2.3. Resonating averages method (RAM)

The principle of this method consists in the separation of the perturbed

Hamiltonian H

(t), written in the interaction picture (Eq. (5)), into an

averaging part,

(t), and an oscillating part

(t), such as :

(t) = H

(t) +

(t)

(14)

with

(t) =

n−1

k=0

)

(15)

and

(t) =

∞

k=n

)

(16)

where (H

)

are a set of constant hermitian operators, and w

a frequency

sequence from which one can extract a subsequence which contains the fre-

quency w

= 0.

The RAM stipulates that if one supposes that this subsequence contains

a set of a ﬁnite number n of frequencies as {w

, w

, ..., w

n−1

}, the other

frequencies {w

, w

n+1

, ...etc} are not harmonic or harmonic combinations

of the n ﬁrst frequencies.

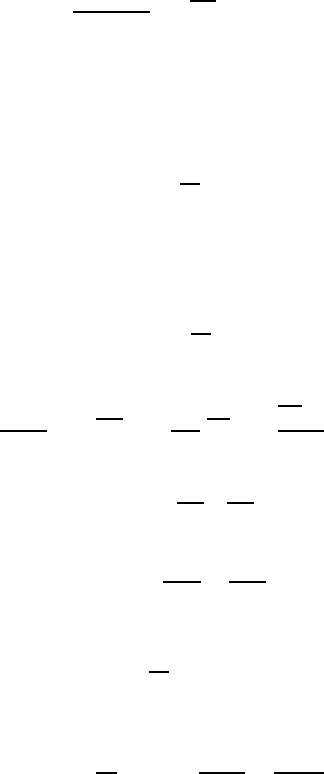
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

294

2.3.1. First order and ﬁrst order ameliorated solutions

The application of the RAM to Eq. (4), to ﬁrst order of µ, gives the diﬀer-

ential equation

(1)

(t)

= µ

(t)

(1)

(t) (17)

With the initial condition

(1)

) = 1, one has

(1)

(t) =

(1)

(t) =

(1)

T (t)e

−i

(1)

Rt/~

(18)

The ﬁrst order ameliorated solution is deﬁned as

(1a)

(t) = [1 −

iµ

(t)]

(1)

(t) (19)

2.3.2. Second order and second order ameliorated solutions

The second order fundamental solution of Eq. (4) is deﬁned by the operator

(2)

(t) = [1 −

iµ

(t)]Γ(t) (20)

where Γ(t) is an unitary operator solution of :

dΓ(t)

= {µ

(t) +

iµ

[

(t) +

(t)

]}Γ(t) (21)

where

(t) =

− H

(22)

(t) =

−

(23)

One may deﬁne the second order ameliorated solution as

(2a)

(t) = [1 −

iµ

(t) + µ

(t)]Γ(t) (24)

where the operator A

(t) is given by

(t) =

{

(t) +

(t)

−

(t)

} (25)

Determination of ﬁrst and second order ameliorated solutions

(1a)

(t)

and

(2a)

(t) (Eqs. (19) and (24)) enables to obtain the ﬁrst and sec-

ond order couples (

(1a)

T (t)), (

(2a)

T (t)) and Floquet-states

(1a)

(t)i, |

(2a)

(t)i, respectively.

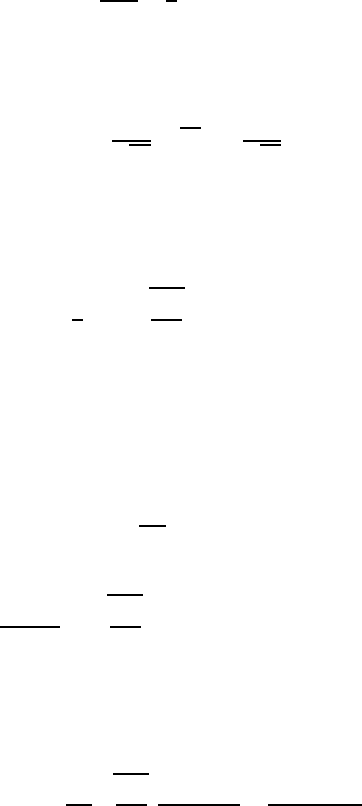
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

295

3. Applications

3.1. Forced harmonic oscillator (FHO)

We have applied the above method, and compared our results to those

of other studies,

which have used other methods, to a FHO with the

following Hamiltonian

H(t, ν

) =

+ µ sin(ν

t)q (26)

where m

and ω

are the constants describing the mass and the frequency

of the unperturbed oscillator, respectively.

By introducing the annihilation operator a

a =

√

(

q + i

√

) (27)

where

= m

(28)

the quantized form of H(t) is

H(t, ν

) = ~ω

a +

) + µ

2β

(a + a

) sin ν

t = H

+ µH

(t) (29)

We applied the RAM to the perturbed Hamiltonian H

(t), expressed in the

interaction picture as Eq. (5), choosing a frequency sequence such as

= 0, ν

− 2ω

, −(ν

− 2ω

) (30)

we deduced from Eq. (29) the averaging and oscillating parts of H

(t), given

respectively by

(t) = 0 (31)

and

(t)

2β

sin ν

t(e

−iω

a + e

iω

) (32)

Then

(t) = α

(t)a + α

∗

(t)a

(33)

where

(t) =

−1

2β

(

i(ν

−ω

− ω

−i(ν

+ω

+ ω

) (34)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

296

3.1.1. First order calculations

The fundamental ﬁrst order ameliorated solution of Eq. (4) is obtained as

(1a)

U(t) = {1 −

(α

(t)a + α

∗

(t)a

)}e

−i

(35)

where

(t) = e

iω

(t) (36)

From Eq. (2), we deduced the Floquet operators such as

(1a)

T (t) = 1 −

(α

(t)a + α

∗

(t)a

) (37)

(1a)

R = H

(38)

The ameliorated ﬁrst order operator

(1a)

R is simply equal to the unper-

turbed Hamiltonian H

This absence of ﬁrst order linear eﬀects in is one of the characteristic

properties of the Floquet Hamiltonian. This fact follows directly from the

perturbative approach applied to the unitary operator (Eq. (19)). However,

it was shown that the phenomenon is deeper for a large class of ﬁeld pulses

which are not necessarily monochromatic, and all odd perturbative correc-

tions must vanish

1426

Then, the eigenstates of the Floquet operator

(1a)

R are obtained as

(1a)

(t)i = e

−i

(1a)

|ni = e

−i(n+

)ω

|ni (39)

and the Floquet states are given by the following expression

(1a)

(t)i = e

−i

(1a)

{|ni −

iµ

[α

(t)

√

n|n −1i + α

∗

(t)

√

n + 1|n + 1i]}

(40)

where

(1a)

= ~ω

(n +

) (41)

To determine the expectation values and the uncertainty relation of the

position and impulsion operators, one can write

q =

2β

(a + a

) (42)

p =

~β

− a)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

297

The ﬁrst ameliorated order expectation values of q, p, q

and p

in the

Floquet states, given by Eq. (40), are

(1a)

qi =

−µ sin ν

(ν

− ω

)

(43)

(1a)

pi =

−µν

cos ν

− ω

(44)

(1a)

i =

2β

{2n + 1 +

[2n(n + 1)Re(α

) + ((2n + 1)

+ 2)|α

]} (45)

(1a)

i =

~β

{2n+1+

[−2n(n+1)Re(α

)+((2n+1)

+2)|α

]} (46)

The explicit expression of the uncertainty product is

(1a)

h∆q∆pi =

(2n + 1){1 + µ

(2n + 1)

~β

(ν

− ω

)

(ν

cos

t + ω

sin

t)}

1/2

(47)

3.1.2. Second order calculations

To solve the diﬀerential equation (21), we begin by expressing the operator

Z(t) in the form

Z(t) = 2Im(α

(t)

dα

∗

(t)

) (48)

Then, we deduce its averaging and oscillating parts as

Z(t) =

−i~

(ν

− ω

)

(49)

Z(t)

i~(e

2iν

+ e

−2iν

)

(ν

− ω

)

(50)

Because H

= 0 and S

= 0,Eq. (21) is reduced to

i~dΓ(t)

iµ

Z(t)Γ(t) (51)

So, we deduce

Γ(t) = e

−iµ

4~m

(ν

−ω

)

(52)

Then, the second order evolution operator is given by

(2)

U(t) = {1 −

(α

(t)a + α

∗

(t)a

)}e

−i

Γ(t) (53)

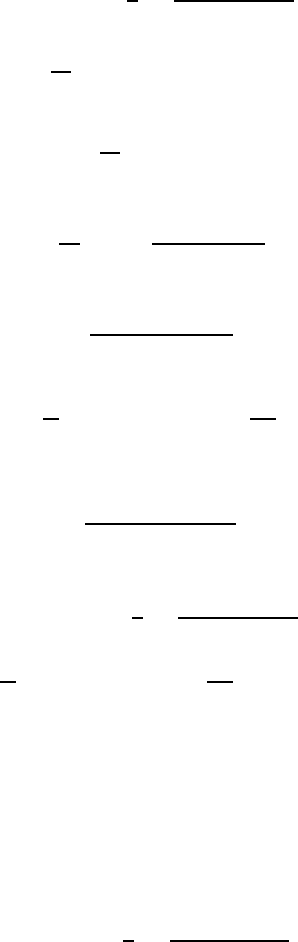
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

298

and the corresponding Floquet components are

(2)

R = ~ω

a +

) +

(ν

− ω

)

(54)

(2)

T (t) = 1 −

(α

(t)a + α

∗

(t)a

) =

(1a)

T (t) (55)

The ameliorated second order solution is

(2a)

(t) = {1 −

(t) + µ

(t)}Γ(t) (56)

with

(t) =

(

S(t) +

Z(t) −

(t)

) (57)

By integrating Eq. (50), we get

Z(t) =

~(e

2iν

− e

2iν

)

(ν

− ω

)

(58)

then,

(2a)

U(t) = {1 −

(α

(t)a + α

∗

(t)a

) −

(ϕ(t)

+α

(t)a

+ α

∗2

(t)a

+ |α

(2a

a + 1))}e

−i

(2a)

Rt/h

(59)

where

ϕ(t) =

−i~ sin ν

t cos ν

(ν

− ω

)

(60)

The ameliorated second order Floquet-Hamiltonian has the following form

(2a)

R = ~ω

a +

) +

(ν

− ω

)

(61)

(2a)

T = 1 −

(α

(t)a + α

∗

(t)a

) −

(ϕ(t) + α

(t)a

+α

∗2

(t)a

+ |α

(2a

a + 1))

(62)

In the same way, we determined the ameliorated second order Floquet states

(2a)

(t)i =

(2a)

T |

(2a)

(t)i (63)

where

(2a)

(t)i = e

−i

(2a)

Rt/~

|ni = e

−i

(2a)

t/~

|ni (64)

and the quasi-energy is

(2a)

= ~ω

(n +

) +

(ν

− ω

)

(65)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

299

The explicit expression of the Floquet states is

(2a)

(t)i = {[1 + ϕ(t) −

(2n + 1)|α

]|ni

−

iµ

[α

(t)

√

n|n −1i + α

∗

(t)

√

n + 1|n + 1i]

(66)

−

[α

(t)

n(n −1)|n − 2i + α

∗2

(t)

(n + 1)(n + 2)|n + 2i]}e

−i

(2a)

Let us notice that the expression of the ameliorated second order Floquet

operator

(2a)

T (t), given by Eq. (62), is comparable to the so-called coher-

ent states generator published by Breuer et al.,

and by Fox et al.,

as well

as the ameliorated second order Floquet states. The detailed comparisons

with these works accompanied with some discussions are given in section

3.1.4.

Moreover, the expression of the quasi-energy (Eq. (65)) is identical to that

given in some other works,

which supports the observations previously

made. Consequently, the corrections are absent to ﬁrst order but appear,

when the approximations are pushed to second order, and are expressed by

a shift D

given by

(ν

− ω

)

(67)

which does not depend on the quantum number n, but on the strength µ

and the pulsation ν

of the interacting ﬁeld. This means eﬀect of the per-

turbation is as a whole spectral shift of all Floquet levels.

This ∆ε is giving by

∆ε = ε

n+1

− ε

(68)

The sense of displacement depends on the sign of D

.If D

> 0 , the levels

shift up and inversely they shift down if D

< 0.

Therefore, the frequency of a transition of the Floquet states, which corre-

sponds to an absorption or emission of the so-called ”Floquet quanta”,

equal to that of the stationary states. So, we can write

(2a)

∆ε = ~

(2a)

(69)

and

(2a)

= ω

(70)