Ammari H., Benkirane A., Touzani A. (editors) Recent Developments in Nonlinear Analysis
Подождите немного. Документ загружается.


December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
310
The second order uncertainty product in Floquet-states
(2a)
|ψ
n
(t)i is ob-
tained in the following form
(2a)
(∆q∆p) =
~
2
(2n + 1)
1 + µ
2
χ
2
(n, ν, t) + µ
4
χ
4
(n, ν, t)
1
2
(149)
where
χ
2
(n, ν, t) =
4
~
2
(n
2
+ n + 4)Re
2
γ
1
(t)
− n(n + 1)Im
2
γ
1
(t)
(150)
χ
4
(n, ν, t) = (2n+1)
2
(ω
0
|f
0
(t)|)
2
8~
2
+
2
~
4
N
m
(n)+2(n
2
+n+4)
2
|γ
1
(t)|
2
2
(151)
3.2.3. Jump operators
From Eqs. (11) and (12) we have determined the ladder operators in the
following forms
A(t) = e
i
∆ε
~
t
a +
2iµ
~
γ
∗
1
(t)a
+
(152)
A
+
(t) = e
−i
∆ε
~
t
a
+
−
2iµ
~
γ
1
(t)a
(153)
where γ
1
(t) is given by Eq. (108)
3.3. Harmonic oscillator with a periodical frequency
We also apply our approach to an Harmonic Oscillator with a periodically
time-varying frequency Ω(t),
5
,
1427
-.
30
We consider the Hamiltonian of the
form
H(t) =
p
2
2m
0
+
1
2
m
0
Ω
2
(t)q
2
(154)
By choosing a Mathieu frequency,
5
,
14
,
2527
-
30
or the so-called experiment’s
Paul trap frequency,
14
,
23
,
2729
-
31
such as
Ω
2
(t) = ω
2
0
(1 + µ cos 2ωt) (155)
where µ and ω are the amplitude and the frequency of the oscillations,
respectively. Then
H(t) =
p
2
2m
0
+
1
2
m
0
ω
2
0
q
2
+
µ
2
m
0
ω
2
0
cos 2ωtq
2
(156)
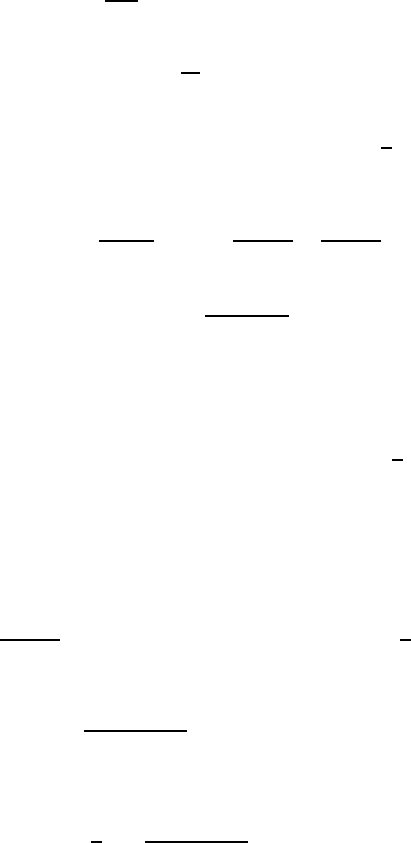
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
311
The quantized form of the perturbation is
H
1
(t) =
~ω
0
4
cos 2ωt(a
2
+ a
+2
+ 2aa
+
+ 1) (157)
The RAM applied to the interaction picture form of H
1
(t) (Eq. (5)) gives
H
I
= 0 (158)
e
H
I
= η
0
(t)a
2
+ η
∗
0
(t)a
+2
+ ~η
2
(t)
aa
+
+
1
2
(159)
where
η
0
(t) =
−i~ω
0
8
e
−2iω
0
t
e
2iωt
ω − ω
0
−
e
−2iωt
ω + ω
0
(160)
η
2
(t) =
ω
0
sin 2ωt
4ω
(161)
Let us remark that our approach is very simple and the Hamiltonian op-
erator of this case is comparable to the one published by Profilo et al.
5
In
fact, if we write
e
H
I
(t) in the standard picture we have,
e
H
1
(t) = η
1
(t)a
2
+ η
∗
1
(t)a
+2
+ ~η
2
(t)
aa
+
+
1
2
(162)
with
η
1
(t) = η
1
(t)e
2iω
0
t
(163)
By differencing this operator, we have
d
e
H
1
(t)
dt
= ˙η
1
(t)a
2
+
˙
η
∗
1
(t)a
+2
+ ~ ˙η
2
(t)
aa
+
+
1
2
(164)
where
˙η
1
(t) =
~ω
0
ω
2
ω
2
− ω
2
0
h
ω cos(2ωt) + 2i sin(2ωt)
i
(165)
By replacing it in the total Hamiltonian, we obtain
b
H(t) = ~Ω
0
(t)
a
+
a +
1
2
+
µ~ω
0
ω
2
ω
2
− ω
2
0
ω cos(2ωt) + 2iω
0
sin(2ωt)
a
2
(166)
+
ω cos(2ωt) − 2iω
0
sin(2ωt)
a
+2

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
312
where
Ω
0
(t) = ω
0
1 +
µ
2
cos 2ωt
(167)
which is a first order development of Ω(t) given in Eq. (155). We see that
this Hamiltonian, where 2ω represents the driven frequency, resembles that
appearing in the context of electromagnetic and acoustic parametric in-
teractions, and is similar to that obtained by Profilo and al.
5
using the
invariant method in the framework of the Lie Group.
3.3.1. First order Floquet operators and Floquet states
From Eq. (19) and with the initial condition
(1)
V
I
(t
0
= 1, one has
(1a)
U
1
(t) =
1 −
iµ
~
e
−iH
0
t/~
e
H
I
e
iH
0
t/~
e
−iH
0
t/~
(168)
From the decomposition of Eq. (2), we determined the first order amelio-
rated Floquet components such as
(1a)
R = H
0
(169)
(1a)
T (t) = 1 −
iµ
~
e
H
1
(t) (170)
where
e
H
1
(t) is given by Eq. (162).
We also remark that, to first order approximation, the operator
(1a)
R is
equal to the simple Oscillator Hamiltonian, and that the operator
(1a)
T (t)
is unitary and periodic with the same period as H
1
(t).
From Eqs. (6) and (8) and using Eqs. (162) and (170), the first order Floquet
states are obtained as
|
(1a)
ψ
n
(t)i = e
−i(n+1/2)ω
0
t
1 −iµη
2
(t)
n +
1
2
|ni (171)
−
iµ
~
h
p
n(n −1)η
1
(t)|n − 2i +
p
(n + 1)(n + 2)η
∗
1
(t)|n + 2i
i
Then, the wave-Floquet function may be written in the form
(1a)
ψ
n
(q, t) = e
−i(n+1/2)ω
0
t
1 −iµη
2
(t)
n +
1
2
ϕ
n
(q) (172)
−
iµ
~
h
p
n(n − 1)η
1
(t)ϕ
n−2
(q) +
p
(n + 1)(n + 2)η
∗
1
(t)ϕ
n+2
(q)
i
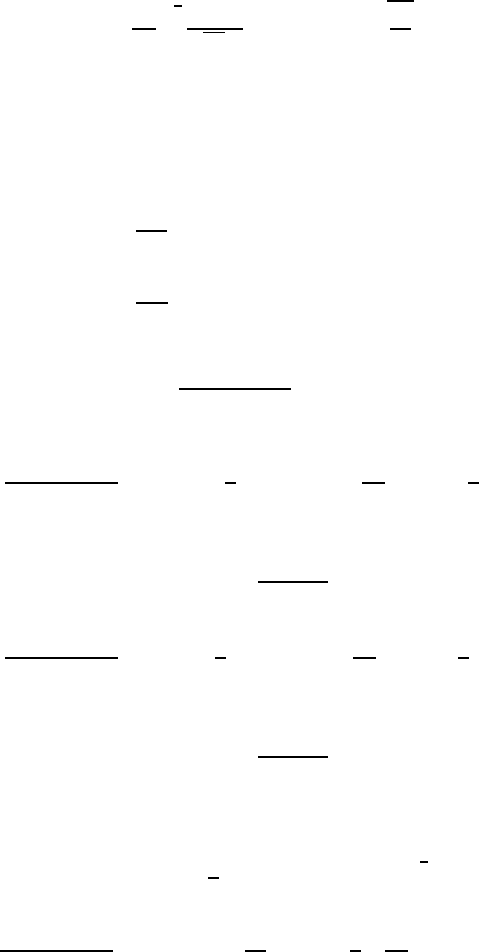
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
313
where
ϕ
n
(q) =
β
0
~π
1
2
1
√
2
n
n!
e
−β
0
q
2
/2~
H
n
r
β
0
~
q
!
(173)
is the wave function of the free oscillator, and H
n
is the Hermite polyno-
mials.
The expectation values of q, p, q
2
and p
2
are deduced, and one has
hqi
n,n
= hpi
n,n
= 0 (174)
h
(1a)
q
2
i
n,n
=
~
2β
0
(2n + 1)
n
1 + µξ
1
(t) + µ
2
ξ
2
(n, t)
o
(175)
h
(1a)
p
2
i
n,n
=
~β
0
2
(2n + 1)
n
1 −µξ
1
(t) + µ
2
ξ
2
(n, t)
o
(176)
where
ξ
1
(t) =
ω
2
0
2
ω
2
− ω
2
0
2
cos(2ωt) (177)
ξ
2
(n, t) =
ω
2
0
32
ω
2
− ω
2
0
5
n
2
+n+
3
2
sin
2
(2ωt)−2
ω
2
0
ω
2
n
2
+n+
1
4
sin
2
(2ωt)
(178)
+(n
2
+ n + 5)
ω
2
0
ω
2
− ω
2
0
ξ
0
2
(n, t) =
ω
2
0
32
ω
2
− ω
2
0
n
2
+n+
7
2
sin
2
(2ωt)−2
ω
2
0
ω
2
n
2
+n+
1
4
sin
2
(2ωt)
(179)
+(n
2
+ n + 5)
ω
2
0
ω
2
− ω
2
0
The first order uncertainty relation in Floquet-states
(1a)
|ψ
n
(t)i is obtained
in the form
(1a)
∆q∆p
n,n
=
~
2
(2n + 1)
1 + µ
2
F
n
(t)
1
2
(180)
F
n
(t) =
ω
2
0
16
ω
2
− ω
2
0
3n
2
+ 3n +
11
4
−2
n +
1
2
2
ω
2
0
ω
2
sin
2
(2ωt) (181)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
314
+
ω
2
0
(ω
2
− ω
2
0
)
n
2
+ n + 1 + 4 sin
2
(2ωt)
The Heisenberg uncertainty condition ∆q∆p ≥
~
2
is satisfied for all time t.
3.3.2. Second order Floquet operators and Floquet states
Solving the differential equation (21) and using Eqs. (22), (23, (158) and
(159), we deduce
Γ(t) = e
−iµ
2
ω
2
0
H
0
t
16~(ω
2
−ω
2
0
)
(182)
Then, the second order evolution operator Eq. (20) is obtained in the form
(2)
U(t) =
1 −
iµ
~
e
H
1
(t)
e
−i
1+µ
2
ω
2
0
16(ω
2
−ω
2
0
)
H
0
t/~
(183)
The corresponding Floquet operators are
(2)
R =
1 + µ
2
ω
2
0
16(ω
2
− ω
2
0
)
H
0
(184)
(2)
T (t) =
(1a)
T (t) (185)
The determination of the ameliorated second order solution (Eq. (24)) ne-
cessitates the calculation of the operators
e
Z
I
(t) and
e
H
2
I
(t) . We get
e
Z
I
(t) = 2~
2
δ
0
(t)
2a
+
a + 1
+ δ
0
2
(t)a
2
− δ
0∗
2
(t)a
+2
(186)
with
δ
0
(t) =
−iω
3
0
2
7
ω
ω
2
− ω
2
0
sin(4ωt) (187)
δ
0
2
(t) =
ω
2
0
2
7
ω
0
e
−4iωt
ω(ω + ω
0
)(2ω + ω
0
)
−
ω
0
e
4iωt
ω(ω − ω
0
)(2ω − ω
0
)
+
2
ω
2
− ω
2
0
e
−2iω
0
t
(188)
and
e
H
2
I
(t) = η
2
0
(t)a
4
+η
∗2
0
(t)a
+4
+
~
2
η
2
2
(t)+2|η
2
0
(t)|
2
a
+
a+
1
2
2
+
3
2
|η
2
0
(t)|
2
(189)
+~η
0
(t)η
2
(t)
2a
+
a + 3
a
2
+ ~
η
0
(t)η
2
(t)
∗
a
+2
2a
+
a + 3

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
315
The operator A
2
(t) , given by Eq. (25), has the following form
A
2
(t) =
1
2~
2
e
Z
I
(t) −
e
H
2
I
(t)
(190)
Therefore, the ameliorated second order evolution operator has the form
(2a)
U(t) =
1+e
−iH
0
t/~
−
iµ
~
e
H
I
+µ
2
A
2
(t)
e
iH
0
t/~
e
−i
1+
µ
2
ω
2
0
16(ω
2
−ω
2
0
)
H
0
t/~
(191)
One may deduce the Floquet operators such as
(2a)
R =
(2)
R (192)
(2a)
T (t) =
(2)
T (t) + µ
2
A
0
2
(t) (193)
with
A
0
2
(t) = e
−iH
0
t/~
A
2
(t)e
iH
0
t/~
(194)
Here the second order correction of has affected the operator
(2)
T (t). Ac-
cording to Eq. (6), the second order Floquet states are given by
|
(2a)
ψ
n
(t)i =
(2a)
T (t)|
(2a)
φ
n
(t)i (195)
where |
(2a)
φ
n
(t)i, the eigenstates of operator
(2a)
R, are such as
|
(2a)
φ
n
(t)i = e
−i(n+
1
2
)(1+
µ
2
ω
2
0
16(ω
2
−ω
2
0
)
)ω
0
t
|ni (196)
The construction of the ameliorated second order Floquet states gives
|
(2a)
ψ
n
(t)i = e
−i
(2a)
ε
n
(ω)t
~
C
n
0
(t)|ni + C
n
−2
(t)|n − 2i + C
n
2
(t)|n + 2i
+C
n
−4
(t)|n − 4i+ C
n
4
(t)|n + 4i
(197)
where the second order quasi-energy is given by
(2a)
ε
n
(ω) = ~ω
0
n +
1
2
1 +
µ
2
ω
2
0
16(ω
2
− ω
2
0
)
(198)
The n-time-dependent coefficients are such as
C
n
0
(t) = 1−iµ
n+
1
2
η
2
(t)+µ
2
−
3
2~
2
|η
1
(t)|
2
+(2n+1)δ
0
(t)+(2n+1)
2
δ
1
(t)
(199)
C
n
−2
(t) =
p
n(n − 1)
−iµ
~
η
1
(t) + µ
2
h
δ
2
(t) + (2n − 1)δ
3
(t)
i
(200)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
316
C
n
2
(t) =
p
(n + 1)(n + 2)
−iµ
~
η
∗
1
(t)+ µ
2
h
−δ
∗
2
(t)+ (2n+ 3)δ
∗
3
(t)
i
(201)
C
n
−4
(t) = µ
2
p
n(n −1)(n − 2)(n −3)δ
4
(t) (202)
C
n
4
(t) = µ
2
p
(n + 1)(n + 2)(n + 3)(n + 4)δ
∗
4
(t) (203)
with
δ
1
(t) =
−1
4
2
~
2
|η
1
(t)|
2
+ η
2
2
(t)
(204)
δ
2
(t) = δ
0
2
(t)e
2iω
0
t
(205)
δ
3
(t) = −
1
2~
η
1
(t)η
2
(t) (206)
δ
4
(t) =
−η
2
1
(t)
2~
2
(207)
The expectation values of q, p, q
2
and p
2
in the |
(2a)
ψ
n
(t)i states are such
as
(2a)
hqi
n,n
=
(2a)
hpi
n,n
= 0 (208)
h
(2a)
q
2
i
n,n
=
~
2β
0
(2n + 1)
1 + µf
n
1
(t) + µ
2
f
n
2+
(t) + µ
3
f
n
3+
(t) + µ
4
f
n
4+
(t)
(209)
h
(2a)
p
2
i
n,n
=
~β
0
2
(2n + 1)
1 −µf
n
1
(t) + µ
2
f
n
2−
(t) + µ
3
f
n
3−
(t) + µ
4
f
n
4−
(t)
(210)
where
f
n
1
=
4Re(iη
1
(t))
~
(211)
f
n
2±
= (2n
2
+ 2n + 7)
|η
1
|
2
~
2
+
n +
1
2
2
η
2
2
+ 2(2n + 1)
2
δ
1
∓4Re(δ
2
) (212)
±4(n
2
+ n + 3)Re(δ
3
) ∓
2i
~
(n
2
+ n + 1)η
2
Im(iη
1
)
f
n
3±
(t) = (2n + 1)
2
η
2
iδ
0
∓ 2Re(iδ
3
)
+
4i
~
(n
2
+ n + 5)Im(η
∗
1
δ
2
) (213)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
317
±
16
~
(n
2
+ n + 3)Re(iη
1
δ
∗
4
) +
20
~
(2n
2
+ 2n + 3)Re(iη
1
δ
∗
3
)
∓
4
~
(2n + 1)
2
δ
1
−
3|η
1
|
2
2~
2
Re(iη
1
)
±4(n
2
+ n + 1)
δ
0
Im(iη
1
)
~
+ iη
2
Im(δ
2
)
2
− Im(δ
3
)
f
n
4±
(t) =
9
4~
4
|η
1
|
2
2
∓
6|η
1
|
2
~
2
Re
(n
2
+ n + 3)δ
3
−δ
2
+ 2(n
2
+ n + 5)|δ
2
|
2
+
(214)
N
0
(n)|δ
3
|
2
+(2n+1)
2
−δ
2
0
±4Re(δ
0
δ
3
)−
3|η
1
|
2
~
2
δ
1
±4δ
1
Re
(n
2
+n+3)δ
3
−δ
2
+(2n + 1)
2
δ
2
1
− 20(2n
2
+ 2n + 3)Re(δ
2
δ
∗
3
) ±(4n
2
+ n + 1)δ
0
Im(2δ
3
−δ
2
)
∓16(n
2
+ n + 3)Re(δ
2
δ
∗
4
) + N
1
(n, 6)|δ
4
|
2
± 2N
1
(n, 4)Re(δ
3
δ
∗
4
)
where
N
0
(n) = 32n(n + 1) + 2(4n
2
+ 4n + 5)(n
2
+ n + 9) (215)
N
1
(n, k)
(n + 4)!
n!
+
n!
(n − 4)!
+ 2
k
(n
2
+ n + 3) (216)
Then, the second order uncertainty relation in Floquet-states
(2a)
|ψ
n
(t)i
has the form
(2a)
(∆q∆p)
n,n
=
~
2
(2n+1)
1+µ
2
χ
n
2
(ν, t)+µ
3
χ
n
3
(ν, t)+µ
4
χ
n
4
(ν, t)
1
2
(217)
where
χ
n
2
(ν, t) = (2n+1)
2
4δ
1
(t)+
η
2
2
(t)
2
+
2
~
2
(2n
2
+2n+7)|η
1
(t)|
2
−
16
~
2
(Re(iη
1
(t))
2
(218)
χ
n
3
(ν, t) = 2i(2n + 1)
2
η
2
(t)δ
0
(t) +
8i
~
(n
2
+ n + 5)Im(η
∗
1
(t)δ
2
(t))+ (219)
40
~
(2n
2
+ 2n + 3)Re(iη
1
(t)δ
∗
3
(t)) +
8
~
Re(iη
1
(t))
4Re(δ
2
(t))
−4(n
2
+ n + 3)Re(δ
3
(t)) +
2i
~
(n
2
+ n + 1)η
2
(t)Im(iη
1
(t))
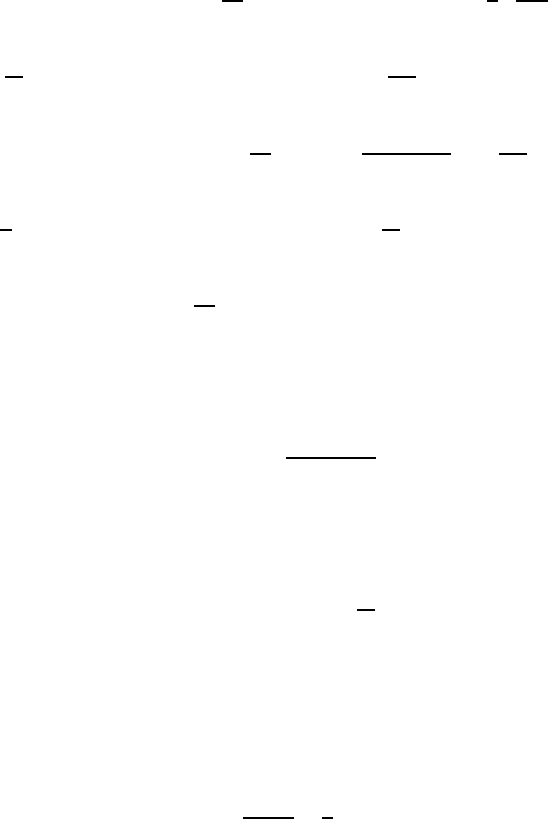
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
318
χ
n
4
(ν, t) = (2n + 1)
2
η
2
2
3
16
(2n + 1)
2
η
2
2
+
3n
2
+ 3n +
1
2
|η
2
1
|
~
2
+ (220)
8i
~
Im(η
1
)Re
n
2
+ n + 3
δ
3
− δ
2
− 2δ
2
0
−
32i
~
Im(η
1
)Re(δ
0
)Re(δ
3
)
+4(n
2
+ n + 1)
(n
2
+ n + 1)
2
~
4
(|η
1
|
2
)
2
−
η
2
2
Re
2
(η
1
)
~
2
+
16i
~
3
Im(η
1
)|η
1
|
2
−
4
~
Re(η
1
)η
2
Re((n
2
+n+3)δ
3
−δ
2
)+Re
2
(δ
2
)+
8i
~
Im(η
1
)
h
Re(δ
0
)Im(δ
2
−2δ
3
)
+Im(δ
0
)Im(δ
2
)
i
+
4
~
4
(n
2
+ n − 3)
2
(|η
1
|
2
)
2
− 4(n
2
+ n + 5)Im
2
(δ
2
)
+
2N
0
(n) − 16(n
2
+ n + 3)
2
Re
2
(δ
3
) − 2N
0
Im
2
(δ
3
) + 2N
1
(n, 6)|δ
4
|
2
−40(2n
2
+ 2n + 3)Im(δ
3
)Im(δ
2
) +
16iIm(η
1
)
~
8(n
2
+ n + 3)
Re(δ
2
)Re(δ
4
)
+Im(δ
2
)Im(δ
4
)
− N
1
(n, 4)
Re(δ
3
)Re(δ
4
) −Im(δ
3
)Im(δ
4
)
−24(2n
2
+ 2n + 1)
Re(δ
3
)Re(δ
2
) +
4i
~
Im(η
1
)Im(δ
0
)Im(δ
3
)
3.4. Harmonic Oscillator with time-dependent mass and
frequency
The last system considered in this study is the time-dependent Harmonic
Oscillator described by the periodically time-varying Hamiltonian such as
H(t) =
p
2
2m(t)
+
1
2
m(t)Ω
2
(t)q
2
(221)
where Ω(t) and m(t) are the time-varying frequency and mass respectively,
given by
Ω
2
(t) = ω
2
(t)(1 + µf(t)) (222)
m(t) = m
0
e
µη(t)
(223)
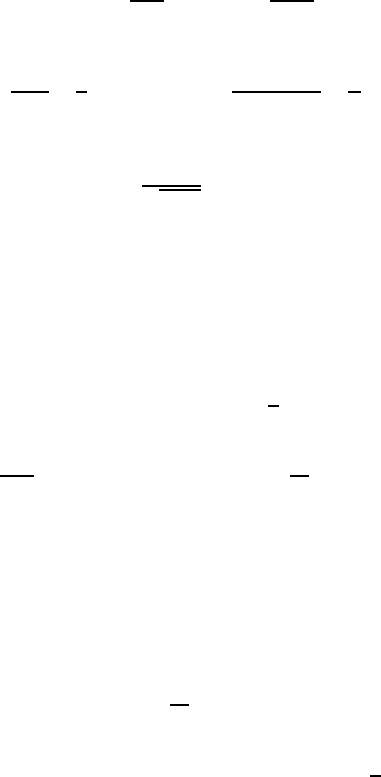
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
319
where µ is the strength of variation of Ω(t) and m(t)
The equations η(t) and f (t) are two periodically time-varying functions
satisfying
η(t + T ) = η(t) (224)
f(t + T ) = f(t)
we introduce the canonical transformations
Q = e
µη(t)
2
q P = e
−µη(t)
2
p (225)
The Hamiltonian becomes
H(Q, P, T ) =
P
2
2m
0
+
1
2
m
0
ω
2
0
Q
2
+ µ ˙η(t)
P Q + QP
2
+
µ
2
m
0
ω
2
0
f(t)Q
2
(226)
we introduce the annihilation and creation operators a and a
+
such as
a =
1
√
2~β
0
(β
0
Q + iP ) (227)
where
β
0
= m
0
ω
0
(228)
By writing the Hamiltonian (Eq. (226)) in the quantized form of Eq. (1),
one can deduce the unperturbed and perturbed Hamiltonians respectively
as
H
0
= ~ω
0
(a
+
a +
1
2
) (229)
H
1
(t) =
~ω
0
4
f(t)(a
2
+ a
+2
+ 2aa
+
+ 1) −
i~
2
˙η(t)(a
2
− a
+2
) (230)
choosing the functions
η(t) = 2 sin νt (231)
f(t) = cos 2ωt
In the interaction picture form of H
1
(t), and using the RAM technique, one
may deduce the averaging and oscillating parts respectively as
H
I
= 0 (232)
e
H
I
= ρ
0
(t)a
2
+ ρ
∗
0
(t)a
+2
+ ~η
2
(t)
aa
+
+
1
2
(233)
