Ammari H., Benkirane A., Touzani A. (editors) Recent Developments in Nonlinear Analysis
Подождите немного. Документ загружается.


December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
300
The corresponding expectation values of the position and momentum op-
erators are given by
h
(2a)
qi =
s
~
2β
0
iµ
~
{2Im(α
1
) +
µ
2
~
2
(2n + 1)[−ϕ(t)Re(α
1
) + |α
1
|
2
Im(α
1
)]}
(71)
h
(2a)
pi = −
s
~
2β
0
µ
~
{2Re(α
1
) +
µ
2
~
2
(2n + 1)[−ϕ(t)Im(α
1
) + |α
1
|
2
Re(α
1
)]}
(72)
h
(2a)
q
2
i =
~
2β
0
{(2n+1)−
4µ
2
~
2
Im(α
1
)+
µ
4
~
4
(2n+1)[
|ϕ(t)|
2
4
+2ϕ(t)Re(α
1
)Im(α
1
)
(73)
+
5(2n
2
+ 2n + 3)
4
Re
4
(α
1
) +
(2n
2
+ 2n + 7)
4
Im
4
(α
1
)
−
(6n
2
+ 6n + 11)
2
Re
2
(α
1
)Im
2
(α
1
)]}
h
(2a)
p
2
i =
~β
0
2
{(2n+ 1)+
4µ
2
~
2
Re(α
1
)+
µ
4
~
4
(2n+ 1)[
|ϕ(t)|
2
4
−2ϕ(t)Re(α
1
)Im(α
1
)
(74)
+
5(2n
2
+ 2n + 3)
4
Im
4
(α
1
) +
(2n
2
+ 2n + 7)
4
Re
4
(α
1
)
−
(6n
2
+ 6n + 11)
2
Re
2
(α
1
)Im
2
(α
1
)]}
and the explicit uncertainty product is
h
(2a)
∆q∆pi =
~
2
(2n + 1){1 +
µ
4
8~
2
m
2
0
(ν
2
0
− ω
2
0
)
2
[
sin
2
2ν
0
t
2ν
2
0
(75)
+
3(2n
2
+ 2n + 1)
ω
2
0
(ν
2
0
− ω
2
0
)
2
(ω
2
0
sin
2
ν
0
t + ν
2
0
cos
2
ν
0
t)]}
3.1.3. Jump operators
In section 2.2, we have defined the operators A(t) and A
+
(t) which are
called jump operators,
315
From Eqs. (11) and (12), we can write, to first
order in µ
A(t) = e
i
(1a)∆ε
~
t (1a)
T (t)a
(1a)
T
+
(t) (76)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
301
A
+
(t) = e
−i
(1a)∆ε
~
t (1a)
T (t)a
+(1a)
T
+
(t) (77)
By substituting the expression (37) of the unitary operator
(1a)
T (t) , we
obtain the two conjugal operators such as,
A(α
1
, t) = a +
iµ
~
α
∗
1
(t) (78)
A
+
(α
1
, t) = a
+
−
iµ
~
α
1
(t) (79)
The action of those ladder operators on the Floquet states |
(
1a)ψ
n
(t)i is
equivalent to the action of the annihilation and creation operators on the
stationary states. These operators are time dependent in the Schr¨odinger
picture. Their expressions (78) and (79) are exactly identical to those pub-
lished by Breuer et al.
3
The operators A(t) and A
+
(t) satisfy the commutation relation
[A(t), A
+
(t)] = 1
One can also give an hermitical symmetric operator
15
N(t) such as
N(t) =
1
2
(AA
+
+ A
+
A) (80)
From the definitions
A(t)|ψ
n
(t)i =
√
n|ψ
n−1
(t)i (81)
A
+
(t)|ψ
n
(t)i =
√
n + 1|ψ
n+1
(t)i (82)
we have
A
+
A|ψ
n
(t)i = n|ψ
n
(t)i (83)
and
AA
+
|ψ
n
(t)i = (n + 1)|ψ
n
(t)i (84)
Then, the exact action of the operator N (t) on the Floquet states is defined
as
N(t)|ψ
n
(t)i = (n +
1
2
)|ψ
n
(t)i (85)
This operator N(t) is equivalent to the number operator of the unperturbed
harmonic oscillator.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
302
3.1.4. Comparisons and discussions
We have presented in the above paragraphs some analytical results of Flo-
quet operators, Floquet states, expectations values and uncertainties prod-
ucts of the position and momentum operators. To test the validity of our
approach and to confirm the accuracy of our calculations, we will give some
direct comparisons with other works given in the literature,
39
-
12
. In partic-
ular, Breuer et al.,
3
have generalized the stochastic wave-function method
to the description of open dissipative systems in strong Laser field, and
have employed the Floquet representation for quantum systems with time-
periodic Hamiltonian, among which the forced harmonic oscillator, submit-
ted to a Laser field with an Hamiltonian of the same form of Eq. (26).
Fox et al.
9
have presented a non perturbative method based on a quasi-
adiabatic method. This approach has been applied to an harmonic oscillator
in an electric field of the form,
E
F
(t) = −eE
0
r
~
2m
0
ω
0
cos ωt(a + a
+
) (86)
To compare our results to those of these authors, we should make some
transformations by using the trigonometric formulation cos x = sin(x +
Π
2
).Then, in all our trigonometric functions (sinus or cosines) we add a
phase (+
Π
2
) i.e. ( our results −→
phase+
Π
2
Fox results)
i)Annihilation and position operators in the Heisenberg picture:
Breuer et al.
3
have calculated the expression of annihilation and position
operators, for the FHO in the Heisenberg picture, to first order in µ. There-
fore, we shall use the evolution operator obtained in Eq. (35) to express
a
H
(t) and q
H
(t).So, we can write
a
H
(t) =
(1a)
U
+
(t)a
(1a)
U(t) (87)
and
q
H
(t) =
(1a)
U
+
(t)q
(1a)
U(t) (88)
we obtain
a
H
(t) = ae
−iω
0
t
+
iµ
0
2
(
e
iν
0
t
ν
0
+ ω
0
+
e
−iν
0
t
ν
0
− ω
0
) (89)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
303
and
q
H
(t) =
s
~
2β
0
{ae
−iω
0
t
+ a
+
e
iω
0
t
+ iµ
0
ω
0
e
iν
0
t
− e
−iν
0
t
ω
2
0
− ν
2
0
} (90)
with
µ
0
=
µ
√
2~β
0
(91)
These expressions are identical to those, a
H
(t, t
0
) and x
H
(t, t
0
), published
by Breuer et al.
3
using the initial condition t
0
= 0 in the integration of the
operator
d
f
H
I
(t)
dt
in Eq. (32) and putting
e
H(0) = 0 and ~ = 1 With those
conditions, we can obtain exact expressions of a
H
(t, t
0
) and x
H
(t, t
0
) given
in reference.
3
But in our approach, we need to have general forms without
imposing any initial condition on our quantum system.
ii)Floquet operator and Floquet states
Let us notice that our ameliorated first order operator
(1a)
T (t) and ame-
liorated second order one
(2a)
T (t) correspond to a first and a second order
development of the Breuer’s operator e
ϕ(t)
D(w) and the Fox’s operator
e
ϕ
F
(t)
D
F
(η), respectively (but for this latter we must take the trigonomet-
ric transformation previously indicated).
Where the so-called coherent state generator
3
is defined by
D(w) = exp(wa
+
− w
∗
a) (92)
By comparing the Breuer’s variable w(t) with our variable α
1
(t) of Eq. (36),
and the Fox’s one η(t), we have the equality
w(t) =
−iµ
~
α
∗
1
(t)(Eq.(116)of[3])
ν
0
t+
π
2
−→ the F ox
0
s variable η(t) (Eq.(35)of[9])
(93)
as well as the phase ϕ(t) obtained in Eq. (60) is directly comparable to the
Breuer’s one ϕ
B
(t) (see the Eq. (120) of reference
3
) and exactly the same
with the Fox’s one ϕ
F
(t) (see Eq. (34) of reference
9
).
iii)Quasi-energy
The Floquet energy given by Eq. (65) is identical to that calculated by
Breuer et al.,
3
Fox et al.,
9
Lefebvre et al.,
10
Maitra et al.
11
and Samal et
al.
12

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
304
iv)Expectation values and uncertainty products
The expectation values of the position q and momentum p operators are
exactly comparable to those given to first order in µ by Fox et al.,
9
but
to second order, our values contain a second order correction term in µ .
Finally, our uncertainty product contains a 2
nd
order correction term in µ
for the case of the ameliorated first order uncertainty relation, while in the
case of ameliorated second order one, it contains a 4
th
order correction term
in µ.
v)Jump operators
Let us notice that the expressions of jump operators given by Eqs. (78)
and (79) are identical to those published by Breuer et al.
3
3.2. Pulsating Harmonic Oscillator
An other good candidate for the application of this formalism is the pul-
sating Harmonic Oscillator described by the periodically time-dependent
Hamiltonian, which is a particular form of the Caldirola-Kanai Hamilto-
nian
16
-
19
H(q, p, t) =
p
2
2m(t)
+
1
2
m(t)ω
2
0
q
2
(94)
where ω
0
is the constant oscillator frequency and m(t) is a periodically
time-varying mass such as
18
m(t) = m
0
e
2µ sin νt
(95)
where µ is the strength of the pulsation and is the mass frequency. We shall
find it convenient to introduce the canonical transformations
Q = q
r
m
m
0
P = p
r
m
0
m
(96)
The Hamiltonian becomes
H(Q, P, t) =
p
2
2m
0
+
1
2
m
0
ω
2
0
Q
2
+
˙m
m
P Q + QP
2
(97)
From the form of Eq. (1), one can deduce the quantized forms of the un-
perturbed and perturbed Hamiltonians, respectively, such as
H
0
= ~ω
0
(a
+
a +
1
2
) (98)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
305
H
1
(t) = −i~ν cos νt(a
2
− a
+2
) (99)
where the annihilation operator a is defined as
a =
1
√
2~β
0
(β
0
Q + iP ) (100)
By using Eqs. (5) and (14) and Eqs. (15) and (16) and choosing a frequency
sequence such as ω
k
= 0, ν − 3ω
0
, −(ν − 3ω
0
)
we deduce
H
I
= 0 (101)
d
f
H
I
(t)
dt
= −i~ν cos νt(e
−2iω
0
t
a
2
− e
2iω
0
t
a
+2
) (102)
Integration of Eq. (102) gives
f
H
I
(t) = γ
0
(t)a
2
+ γ
∗
0
(t)a
+2
(103)
where
γ
0
(t) = −
~ν
ν
2
− 4ω
2
0
e
−2iω
0
t
(2ω
0
cos νt + iν sin νt) (104)
3.2.1. First order solutions
i)Floquet operators
By solving Eq. (4), using Eq. (103) and from Eq. (19), one can write
(1a)
U
1
(t) =
1 −
iµ
~
e
−iω
0
ta
+
a
e
H
I
e
iω
0
ta
+
a
e
−iH
0
t/~
=
(1a)
T (t)e
−i
(1a)
Rt/~
(105)
and deduce the first order ameliorated Floquet components such as
(1a)
R = H
0
(106)
(1a)
T (t) = 1 −
iµ
~
γ
1
(t)a
2
+ γ
∗
1
(t)a
+2
(107)
with
γ
1
(t) = e
2iω
0
t
γ
0
(t) (108)
For a comparison with other works, we will calculate the position operator
in the Heisenberg picture, by using the first order ameliorated evolution
operator of Eq. (105). So one may write
Q
H
(t) =
(1a)
U
+
1
(t)Q
(1a)
U
1
(t) (109)
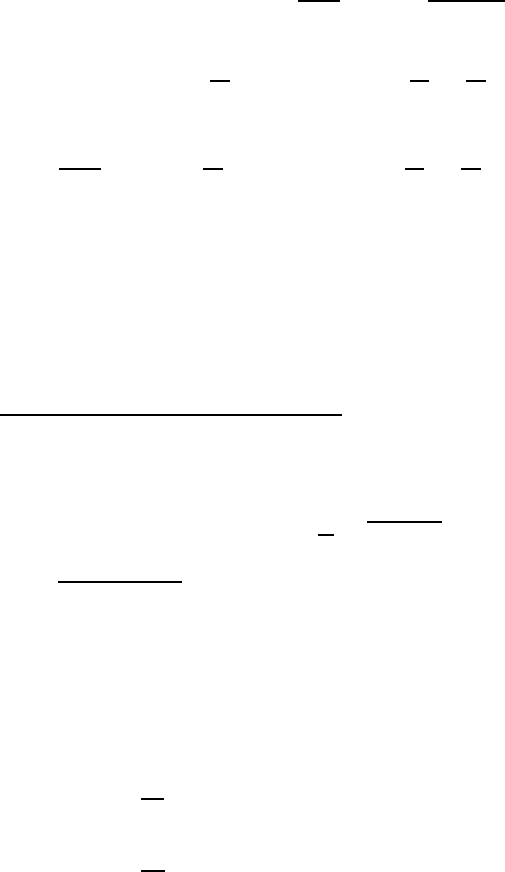
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
306
To first order of µ we get
Q
H
(t) = Q(0) cos ω
0
t +
P (0)
β
0
sin ω
0
t +
4µν
4ω
2
0
− ν
2
× (110)
(
Q(0)
"
ω
0
2 cos
2
νt
2
− 1
!
sin ω
0
t − ν sin
νt
2
cos
νt
2
cos ω
0
t
#
+
P (0)
β
0
"
ω
0
2 sin
2
νt
2
− 1
!
cos ω
0
t −ν sin
νt
2
cos
νt
2
sin ω
0
t
#)
with Q(0) = Q and P (0) = P. (111)
If we take into account the initial condition
e
H(0) = 0 in the integration of
Eq. (102), this result is rather comparable with that obtained by Abdalla
et al.
18
which have employed the method of the perturbation theory. The
comparison is also verified for P
H
(t) and a
H
(t).
ii)Floquet states and uncertainty relation
From Eqs. (6) and (8) and using Eqs. (106) and (107), we have calculated
the first order Floquet states,
|
(1a)
ψ
n
(t)i = e
−i(n+1/2)ω
0
t
(
|ni −
iµ
~
"
p
n(n − 1)γ
1
(t)|n − 2i
+
p
(n + 1)(n + 2)γ
∗
1
(t)|n + 2i
#)
(112)
The expectation values of q, p, q
2
and p
2
are
hqi = 0 (113)
hpi = 0 (114)
h
(1a)
q
2
i =
~
2β
(2n + 1){1 + µF
1
(n, ν, t) + µ
2
F
2
(n, ν, t)} (115)
h
(1a)
p
2
i =
~β
2
(2n + 1){1 −µF
1
(n, ν, t) + µ
2
F
2
(n, ν, t)} (116)
where
β(t) = m(t)ω
0
(117)
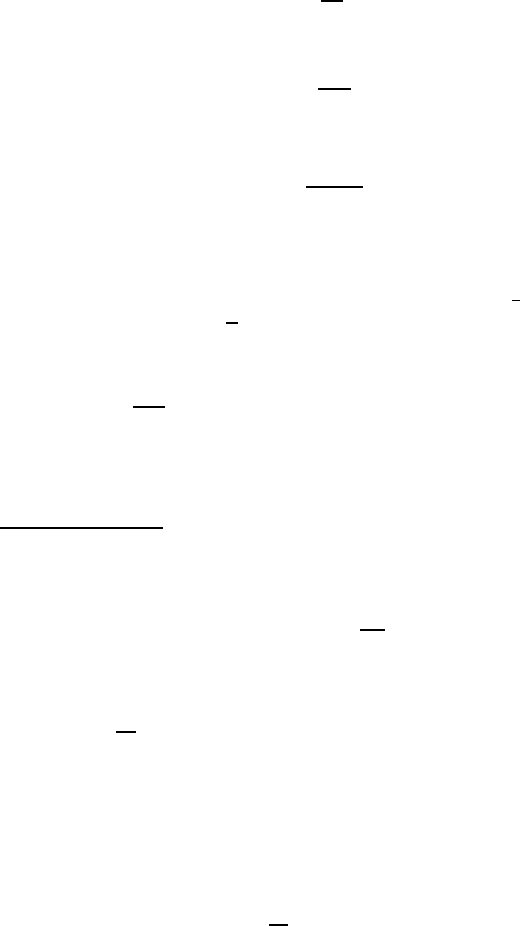
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
307
F
1
(n, ν, t) = λ
0
sin νt (118)
F
2
(n, ν, t) = (n
2
+ n + 5)
λ
1
2
(λ
2
0
sin
2
νt + cos
2
νt) (119)
with
λ
0
=
ν
2ω
0
(120)
and
λ
1
=
4ν
2
0
ω
2
0
− 1
(121)
Finally, calculation of the uncertainty relation in the Floquet-states
(1a)
|ψ
n
(t)i gives
(1a)
(∆q∆p) =
~
2
(2n + 1)
1 + µ
2
(1a)
F (n, ν, t)
1
2
(122)
(1a)
F (n, ν, t) =
λ
2
1
4λ
2
0
n
2
+n+1
λ
2
0
sin
2
νt+cos
2
νt
+4 cos
2
νt
(123)
3.2.2. Second order solutions
i)Floquet operators
Solving the differential equation (21) and using Eqs. (101) and (103) we
deduce
Γ(t) = e
−iµ
2
λ
1
H
0
t
~
(124)
Then, the second order solution (Eq. (20)) is obtained in the following form
(2)
U(t) =
1−
iµ
~
e
−iω
0
ta
+
a
e
H
I
e
iω
0
ta
+
a
e
−i(1+µ
2
λ
1
)H
0
t/~
=
(2)
T (t)e
−i
(2)
Rt/~
(125)
Consequently, the second order Floquet operators are
(2)
R =
1 + µ
2
λ
1
H
0
(126)
(2)
T (t) = 1 −
iµ
~
γ
1
(t)a
2
+ γ
∗
1
(t)a
+2
(127)

December 29, 2009 9:37 WSPC - Proceedings Trim Size: 9in x 6in recent
308
One observes that a µ-second order correction appears in
(1a)
R. Therefore,
the ameliorated second order evolution operator is
(2a)
U(t) =
1 + e
−iH
0
t/~
−
iµ
~
e
H
I
+ µ
2
A
2
(t)
e
iH
0
t/~
e
−i(1+µ
2
λ
1
)H
0
t/~
(128)
because
e
S
I
(t) = 0 (129)
then
A
2
(t) = −
1
2~
2
f
0
(t)H
0
+
γ
0
(t)a
2
+ γ
∗
0
(t)a
+2
2
(130)
where
f
0
(t) = i~λ
1
sin 2νt
ν
(131)
Then, we deduce
(2a)
R =
(2)
R (132)
(2a)
T (t) = 1−
iµ
~
γ
1
(t)a
2
+γ
∗
1
(t)a
+2
−
µ
2
2~
2
f
0
(t)H
0
+2|γ
1
(t)|
2
H
2
0
~
2
0
ω
2
0
+
3
4
(133)
+γ
2
1
(t)a
4
+ γ
∗2
1
(t)a
+4
A second order correction term in µ is also present in the operator
(2a)
T (t)
ii)Floquet states
The eigenstates of the operator
(2a)
R have the following form
(2a)
|φ
n
i = e
−i(n+
1
2
)(1+µ
2
λ
2
1
)ω
0
t
|ni (134)
From Eq. (6) and using Eq. (133), the construction of the ameliorated
second order Floquet states leads to
(2a)
|ψ
n
i = e
−i(n+
1
2
)(1+µ
2
λ
2
1
)ω
0
t
C
n
0
(t)|ni + C
n
−2
(t)|n − 2i
+C
n
2
(t)|n + 2i+ C
n
−4
(t)|n −4i + C
n
4
(t)|n + 4i
(135)
where the n-time-functions are
C
n
0
(t) = 1 −
µ
2
2~
2
n +
1
2
~ω
0
f
0
(t) + 2(n
2
+ n + 1)|γ
1
(t)|
2
(136)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
309
C
n
−2
(t) = −
iµ
~
p
n(n −1)γ
1
(t) (137)
C
n
2
(t) = −
iµ
~
p
(n + 1)(n + 2)γ
∗
1
(t) (138)
C
n
−4
(t) = −
µ
2
2~
2
p
n(n −1)(n − 2)(n −3)γ
2
1
(t) (139)
C
n
4
(t) = −
µ
2
2~
2
p
(n + 1)(n + 2)(n + 3)(n + 4)γ
∗2
1
(t) (140)
iii)Heisenberg uncertainty relation
The expectation values of q , p and q
2
in the |
(2a)
ψ
n
(t)i states are
(2a)
hqi =
(2a)
hpi = 0 (141)
h
(2a)
q
2
i =
~
2β
(2n+1)
n
1+µM
1
(ν, t)+µ
2
M
2
(ν, t)+µ
3
M
3
(ν, t)+µ
4
M
4
(ν, t)
o
(142)
h
(2a)
p
2
i =
~β
2
(2n+1)
n
1−µM
1
(ν, t)+µ
2
M
2
(ν, t)−µ
3
M
3
(ν, t)+µ
4
M
4
(ν, t)
o
(143)
where
M
1
(ν, t) =
4i
~
Im(γ
1
(t)) (144)
M
2
(ν, t) = 2(n
2
+ n + 4)
|γ
1
(t)|
2
~
2
(145)
M
3
(ν, t) =
i
~
3
4(n
2
+ n + 5)|γ
1
(t)|
2
Imγ
1
− (n
2
+ n + 1)~ω
0
Re(γ
1
)f
0
(t)
(146)
M
4
(ν, t) =
N
m
(n)
~
4
|γ
2
1
(t)|
2
− (2n + 1)
2
ω
0
f
0
(t)
4~
2
(147)
with
N
m
(n) =
1
4
(n
2
+ n + 2)(n
2
+ n + 52) + (n
2
+ n + 1)
2
+ 1 (148)
