Анастасиади Г.П. Конспект лекций по курсу управление качеством
Подождите немного. Документ загружается.

Таким образом, процесс измерения является необходимым видом деятельности в
процессе производства продукции и при установлении уровня ее качества на всех этапах
жизненного цикла, включая и потребление (эксплуатацию). Причем, утверждение,
бытующее в недавние времена – “отгрузил продукцию, можешь забыть”, в рыночной
системе превращается в – “продавай дешево, обслуживай дорого”, то есть измерение
качества прекращается только после утилизации продукции.
Примечание.
Три краеугольных камня управления составляют фундамент управления качеством:
• система понятий и определений;
• системные модели производства и системные методы анализа;
• достаточный перечень показателей и обеспеченность их измерений.
Совершенно очевидно, что отсутствие любого из них превратит управление качеством
продукции в поиски черной кошки ночью в темной комнате. По большому счету, состояние
отечественных предприятий определяется именно проблемами в фундаменте. Из-за
стыдливого умалчивания о достигнутом мировым сообществом уровня качества продукции
и обслуживания система понятий, определений и требований к качеству не формулируется,
системные модели, способные достигнуть необходимый уровень качества не создаются,
перечень показателей не устанавливается. Никто не публикует (не устанавливает?) перечень
показателей безопасности для легковых автомобилей, по-видимому, потому что на
отечественных заводах автомобили придется браковать прямо на конвейере. Современный
уровень качества таков, что, если измерение показателей качества не производится, то
ничего не производится.
Контрольные вопросы к главе 4.
1. Как зависит количество производимой продукции от уровня ее качества при
фиксированных ресурсах?
Ответ: зависимость обратно пропорциональная.
2. Как влияет индустриальное развитие на зависимость количества от уровня качества?
Ответ: повышение качества увеличивает реализацию продукции потребителю.
3. В каком случае равновесная цена рынка может снижаться при повышении качества?
Приведите примеры.
Ответ: рынок компьютеров.
4. В чем заключаются 4 базовых понятия об эксперименте?
91
Ответ: качественные измерения, расплывчатые наблюдения, погрешности,
статистические измерения.
5. Что можно установить по номинальной шкале измерений?
Ответ: адреса, наименования.
6. По какой шкале определяет преподаватель оценки на экзамене?
Ответ: по шкале порядка.
7. Где применяются модифицированные порядковые шкалы?
Ответ: при экспертных оценках и измерениях по реперным точкам.
8. По какой шкале определяются температура, расстояние на местности, глубина или
высота?
Ответ: по шкале интервалов.
Глава 5. СЛУЧАЙНОСТЬ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И ДЕФЕКТЫ
Информация как свойство материи. Сигналы в системах. Случайные события,
распределение и плотность распределения. Закон больших чисел. Эмпирическое и
теоретическое распределение непрерывной и дискретной величины. Основные виды
распределения вероятностей – нормальное, пуассоновское, их характеристики. Примеры:
качество материалов – нормальное распределение, телефонное обслуживание –
пуассоновское. Физическая природа вероятностного описания – дефекты: критические,
существенные, малосущественные. Статистическая обработка результатов измерений –
гистограмма, характеристики выборки, установление распределения вероятностей, анализ
результатов, установление технических требований.
Философский смысл понятия информация [3] заключается в знаниях, сведениях,
сообщениях, уведомлениях, известиях, ведомостях, т.е. в чем-то присущем человеческому
сознанию и общению, в современном понимании распространяется и не неорганическую
природу – на материю вообще.
Информация – это отражение состояния одного объекта в соответствующем
состоянии другого. Показания прибора отражают информацию о состоянии системы,
например отклонение стрелки амперметра сообщает информацию о силе проходящего тока.
Кибернетика – это наука, которая занимается изучением систем любой природы,
способных воспринимать, хранить и перерабатывать информацию и использовать ее
для управления и регулирования.
92

Соответствие состояний возникает в результате взаимодействия объектов, как
правило, физического. Материальным носителем информации является сигнал о состоянии
объектов. Сигналы бывают статические используемые для хранения информации (книга), и
динамические – для передачи (волны). Сигналы распространяются в шуме.
Измеренных состояний системы может быть сколько угодно, не столько по величине,
сколько по различиям между ними, определяемым точностью измерения. Следовательно,
результат измерения является случайным или вероятностным. Как отмечалось выше,
установление качества продукции или услуг непосредственно связано с измерениями
некоторых характеристик. Причем, на этапе сравнения измеряемой величины могут
применяться как эталоны (международные или национальные) так и различные шкалы,
имеющие единицы измерения (масштаб), реперные (опорные) точки или их не имеющие. В
первом случае это принятая система мер (например – метр, килограмм, секунда), во втором
– шкала твердости по Моосу, землетрясений по Рихтеру или ветра по Бюффону, в третьем
случае имеют дело с расплывчатыми описаниями ситуации, например, люблю – нравится –
безразлично – не люблю. В первом случае измерение может быть выполнено с точностью,
определяемой классом приспособления и квалификацией оператора, обычно погрешность
составляет доли процента. Во втором и третьем случаях само измерение является условным
и полностью определяется квалификацией оператора –эксперта. Поэтому принятая в
терминах управления качеством методика измерений основана на многократном повторении
процесса, чтобы при последующем анализе избежать субъективных и объективных,
случайных и систематических ошибок. Эти методы рассматриваются в теории вероятности и
математической статистике. Здесь мы кратко рассмотрим методы, относящиеся к
установлению качества, обнаружению и предупреждению появления дефектов продукции и
сбоев в системах обслуживания. Любой технологический процесс и обслуживание при этом
рассматриваются как случайные процессы при заданных ограничениях.
Рассмотрим кратко некоторые основные понятия теории вероятности.
Случайная величина – это некоторая переменная, принимающая в зависимости от
случая те или иные значения с определенными вероятностями.
Испытания Бернулли – независимые испытания с двумя случайными исходами
(удача и неудача), вероятность которых не изменяется от испытания к испытанию.
Если вероятность удачи равна p, тогда вероятность неудачи q=1–p. Например, при
двух испытаниях, различные исходы можно определить квадратом суммы
(p+q)
2
=p
2
+2pq+q
2
=1
93
Здесь первый член определяет вероятность двух удач, последний – двух неудач, а
второй – одной удачи и неудачи. В общем виде формула для определения вероятности
появления k удач в n опытах имеет вид
Р(k)=C
n
k
p
k
q
n–k
Это распределение называется биномиальным.
Если имеются доказательства, что процесс генерирует результаты в соответствии
теоретическим законом распределения, тогда задача испытаний состоит в том, чтобы
определить параметры, описывающие распределение. В противном случае, необходимо
провести доказательство этого соответствия. В обоих случаях необходимо установить
истинное (опытное, выборочное) распределение вероятности. В таких условиях каждому
испытанию из проведенных присваивают вероятность, вероятность совпадающих
результатов складывают. Распределение вероятностей характеризуется по крайней мере
двумя параметрами – математическим ожиданием a (средним x
ср
) и дисперсией
(теоретической s и выборочной S), которые определяются следующими соотношениями
∞
а = ∫ p(x)∂x,
−∞
∞
s
2
= ∫ (x–a)
2
p(x)∂x,
−∞
x
ср
=(1/n)
∑
=
n
j 1
х
j
,
S
2
=(1/n)
∑
=
n
j 1
(х
j
– а)
2
Для построения эмпирического распределения весь разброс наблюдаемых значений
разбивают на k интервалов, подсчитывают частоту результатов в каждом интервале n
k
/N и
94

наносят на диаграмму в различном виде, если в виде столбцов – то диаграмму называют
гистограмма. Построение гистограммы является первичной обработкой
экспериментальных данных, в значительной степени расширяющей объем информации и
позволяющей управлять имеющимися данными, т.е. оценивать предварительно качество
эксперимента, планировать мероприятия по его использованию и др.
Пример: оценка собранного урожая яблок.
Стабильный размер яблок является товарной характеристикой продукции,
определяющей показатель качества (сорт) и цену реализации, причем более высокое
качество возможно при снижении цены. Рынок фруктов заполнен французскими,
аргентинскими, австралийскими яблоками, отечественная продукция с неясными
показателями качества практически не имеет конкурентной способности. По французским
стандартам разброс размеров яблок первого сорта не должен превышать 5% или разброс
массы не более 15%. Если средняя масса яблок сорта «Гольден» составляет 200 грамм, то
допустимые пределы калибровки 185…215 грамм. Проведем анализ урожая яблок сорта
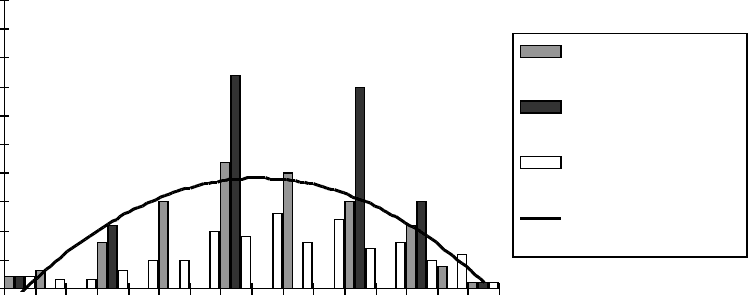
«Белый налив». На рис. 8 приведена гистограмма распределения массы яблок, собранных с
одного дерева, соответствующая табл. 2.
Таблица 2
Распределение яблок, собранных с одного дерева, по массе
(выборка 100 яблок, x
ср
=170, S=35 )
Масса,
грамм
<100 100
<120
120
<140
140
<160
160
<180
180
<200
200
<220
220
<240
>240
240
Частота,
n
k
/N,%
2 3 7 14 22 20 15 11 4
95
0
5
10
15
20
25
30
35
40
45
50
<100
120
140
160
180
200
220
>240
m
n/N (20g)
n/N (40g)
n/N (10g)
Ïîëèíîìèàëüíûé (n/N
(20g))
Рис. 8. Гистограмма распределения яблок по массе (данные таблицы 2), три варианта
выбора интервалов – 10, 20 и 40 грамм
Даже на начальном этапе обработки пришлось столкнуться с определенными
трудностями, в частности, с выбором интервала разбиения. Малый интервал (10 грамм)
приводит к пилообразному распределению частот, что не имеет смысла. Большой интервал
(40 грамм) приводит к равномерному распределению, противоречащему понятию качества.
Наиболее приемлемый интервал для данной выборки – 20 грамм. В стандартный интервал –
15% (±15 грамм) попадает примерно 25% урожая.
Первичная обработка данных эксперимента также требует определенной
квалификации специалиста. При отсутствии дополнительных оснований интервалы
разбиений следует выбирать равными в количестве около 10.
Случайные величины бывают двух видов – непрерывные и дискретные. Например:
размеры, масса, углы – непрерывные; отказы, дефекты, удачи–неудачи – дискретные.
Существуют методы представления дискретных величин в виде непрерывных и наоборот,
естественно, что для этого необходимо иметь представление о физической сущности
исследуемого процесса.
Функции вероятности случайной величины подчиняются следующим правилам.
1. Правило нормировки вероятностей.
Интеграл функции вероятности по возможным пределам равен 1.
∞
96
∫ p(x,a,s)∂x =1,
−∞
Это правило очевидно и не нуждается в пояснениях.
2. Закон сложения вероятностей.
Вероятность события А(А
1
∪ А
2
), являющегося объединением непересекающихся событий
А
1
и А
2
равна сумме их вероятностей
Р(А)=Р(А
1
∪ А
2
)=Р(А
1
) + Р(А
2
)
Пример: если на 100 человек населения за 1 год рождается 1 мальчик (событие А
1
) и 1
девочка (событие А
2
), то это означает, что рождается 2 ребенка (событие А(А
1
∪ А
2
) в
год на 100 жителей.
3. Закон умножения вероятностей.
Вероятность события А(А
1
∩ А
2
), являющегося совмещением событий А
1
и А
2
равна
произведению их вероятностей
Р(А)=Р(А
1
∩ А
2
)=Р(А
1
) * Р(А
2
)
Пример: вероятность рождения мальчика и девочки можно считать равной 0.5, тогда
вероятность рождения в одной семье с двумя детьми двух мальчиков или двух девочек
(событие А(А
1
∩ А
2
) равна 0.25.
4. В соответствии с предельными теоремами теории вероятностей при последовательных
независимых испытаниях частота событий k/n приближается к вероятности (p), a
выборочное среднее (x
ср
) к математическому ожиданию (a) или
P{k/n–p>ε}→0 и
P{x
ср
–a>ε}→0,
при n→∝ и ε>0.
97
Формулируется это следующим образом: при n, стремящемся к бесконечности, и любом
положительном ε, вероятность того, что частота отличается от вероятности (среднее
отличается от математического ожидания) на величину, большую ε, стремится к нулю.
Следствие: увеличение числа испытаний повышает достоверность результатов
исследования.
Управление качеством состоит из действий с большим числом единиц продукции,
состоящей, по крайней мере, из двух категорий – брак и годная. При этом должно быть
обеспечено разделение продукции с направлением годной на дальнейшую реализацию и
изоляцией брака для принятия решения. Важнейшим элементом управления является
контроль качества продукции, проводимый с применением статистических методов,
основой которых являются испытания случайным образом отобранных образцов – выборки.
Выборка и испытания могут быть реализованы двумя способами – без возвращения и с
возвращением испытанных образцов в производственный процесс. Обычно применяется
метод без возвращения, при этом показатели качества в объеме продукции изменяются.
Например, если установившийся технологический процесс обеспечивает 95 годных на 100
произведенных изделий, то изъятие 1 изделия без возвращения будет означать, что в 99
оставшихся будет или 94 годных и 5 дефектных или 95 годных и 4 дефектных изделия.
Вероятность извлечения k дефектных из объема n изделий, состоящего из D дефектных и n–
D годных при m испытаниях подчиняется гипергеометрическому закону распределения
Р(k)= C
k
D
*C
n-k
n-D
/C
m
n
=
C
k
m
*[D/n*(D-1)/(n-1)*...*(D-k+1)/(n-k+1)]*
[(n-D)/(n-k)*(n-D-1/(n-k-1)*...*(n-D-m+k+1)/(n-D-m+1)],
k=0, 1, ... m
где C
m
n
– число сочетаний из n по m.
Здесь реализуется закон умножения вероятностей событий обнаружения дефектных и
годных изделий. Вычисление числа сочетаний трудоемко, поэтому составляют специальные
таблицы.
Математическое ожидание количества дефектов в выборке
а=mD/n.
Дисперсия
98
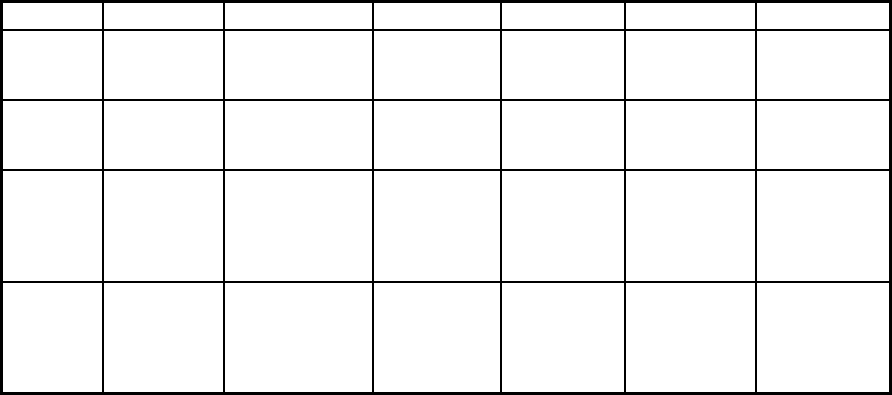
s
2
=mD(n-m)/(n-1)
При большом числе изделий и малой выборке распределение без возвращения
приближается к распределению с возвращением, описываемому биноминальным законом
Р(k)=C
k
m
*p
k
*(1-p)
k
,
Математическое ожидание количества дефектов в выборке
а=mD/n.
Дисперсия
s
2
=mp(1-p),
где p=D/n.
Для n=100, p=0.05 и m=5 различие в вероятности гипергеометрического,
биномиального и пуассоновского (см. ниже) распределений приведено в табл. 3. Следует
отметить, что пуассоновское распределение, применяемое при малых p<0.1, имеет
аналитический вид и наиболее удобно для вычислений.
Таблица 3
Сравнение вероятности обнаружения к дефектных изделий в выборке m=5 при p=0.05
(гипергеометрическое (Gg) и биномиальное (Bin) распределение)
k 0 1 2 3 4 5
P(k),
Gg
0.769590 0.211425 0.018381 0.000593 0.000006 0.0000000
12
P(k),
Bin
0.773780 0.203600 0.021434 0.001128 0.0000295 0.0000003
00
∆Р(k),
%
–0.0042
(–0.5%)
0.007825
(+3.7%)
–0.00305
(–16%)
–0.00053
(–90%)
–0.000023
(–400%)
0.0000002
88 (–
2400 %)
P(k)
Puass
0.7788 0.1947 0.0243 0.0020 0.0001260 0.0000063
00
99

Следует отметить, что особенно большое различие имеется при оценке вероятности
многих (всех возможных) дефектов, оно может достигать десятков раз. Реальные проблемы
возникают при анализе дефектов, способных привести к авариям, это возможно только при
совмещении отказов разных ступеней защиты и здесь необходимо иметь в виду следующие
условия:
1) вероятность совмещения отказов систем защиты всегда больше нуля;
2) закон распределения вероятности, как правило, неизвестен, и следует применять такой,
который дает наибольшую вероятность;
3) действия оператора, совершившего первую ошибку, как следует из анализа причин
аварий, снижают степень независимости остальных ступеней защиты, следовательно
возможность второй и последующих ошибок становится более реальной и определяется
не техническими, а психологическими факторами.
Таким образом, оценка вероятности по биномиальному распределению бездефектной
(k=0) продукции и обнаружения в выборке 1 дефекта (k=1) приемлема, для большего
количества дефектов – сильно завышена.
При p<0.1 для оценки может быть использовано распределение Пуассона (подробнее
см. ниже)
Р(k)=(m*p)
k
*exp(–m*p)/k!.
Математическое ожидание и дисперсия равные
а= s
2
=mр.
Распределение Пуассона может быть использовано при таких исходных данных
только для оценки вероятности отсутствия дефектов (k=0).
Оценка по формуле Лапласа определяет вероятность попадания результатов в
интервал значений Z
1
и
Z
2
Z2
Р(k)=
1/
(√2π)∗∫ exp(–Z
2
/2)∂Z и
100
