Andrews Dawid G. An Introduction to Atmospheric Physics

Подождите немного. Документ загружается.

199 An energy balance model

If this steady state is now slightly perturbed, so that T = T



(t) and U = U



(t),

where T



 T

and U



 U

, we obtain the linearised form



= Q(T

+ T



, U

+ U



)

≈

∂Q

∂T



∂Q

∂U



, (8.5)

where we have expanded Q(T, U) to ﬁrst order in T



and U



and used equation (8.4).The

partial derivatives are evaluated at (T, U) = (T

, U

We now deﬁne the climate feedback parameter

α =−

∂Q

∂T

. (8.6)

An analogy with feedback in a simple electronic circuit can be made by considering an

electromotive force E across an inductance L that carries current I,sothatE = LdI/dt.A

feedback is present if E depends on I, for example through the linear relation E = F −αI

where F and α are constants.

The climate feedback parameter α quantiﬁes how the net downward heat ﬂux Q varies

with temperature. If Q decreases with temperature, α is positive and tends to damp temper-

ature perturbations. On the other hand if Q increases with temperature, α is negative and

tends to enhance temperature perturbations.

In Section 8.4 we examine in more detail the processes that contribute to climate feed-

back. As noted there, typical global-mean values of α are positive under current climate

conditions, though under extreme climates they might become negative.

We also deﬁne the radiative forcing

F =

∂Q

∂U



(8.7)

so that equation (8.5) can be written



+ αT



= F(t ). (8.8)

The radiative forcing F as deﬁned in equation (8.7) quantiﬁes the change in the net

inward heat ﬂux F

↓

− F

↑

at the top of the troposphere associated with a small change U



of a greenhouse gas from its steady-state value. As we have seen in Section 8.1, it can be

deﬁned more generally for a ﬁnite change and applied to quantities other than greenhouse

gases.

It is not possible to give precise values of the feedback parameter or the heat capacity for

the Earth’s climate system. However, experiments with the complex climate models cited

in Solomon et al. (2007) suggest that α ≈ 1Wm

−2

−1

and C ≈ 1GJK

−1

−2

might be

typical order-of-magnitude estimates.

It should be noted that our linearised EBM (8.8) ignores the possibility of climate change

in the absence of an external forcing; this might be brought about, for example, by non-linear

interactions between different components of the climate system.

200 Climate change

8.3 Some solutions of the linearised energy balance model

Equation (8.8) is a ﬁrst-order linear differential equation for the deviation T



of the global-

mean temperature from its steady-state value T

. A formal solution of this equation, for

arbitrary radiative forcing F(t) and suitable initial conditions, can easily be obtained by

the standard ‘integrating factor’ method, as outlined below. In this section we assume that

α>0.

Note that the quantity

τ =

(8.9)

has the dimensions of time: it is in fact a relaxation time, but is also called the feedback

response time (FRT). Using the order-of-magnitude estimates of C and α quoted in the

previous section, we expect τ to be roughly on the order of 10

s ≈ 30 years for the Earth’s

climate system.

To solve equation (8.8) we divide by C and multiply by the integrating factor exp(t/τ )

to get





t/τ



F(t)

t/τ

. (8.10)

We assume that T



= 0 at an initial time t = 0, and integrate equation (8.10) to obtain the

formal solution



(t) =

−t/τ



F(u) e

u/τ

du. (8.11)

To get a feel for the behaviour of solutions of the form (8.11), we look at the responses

to a few simple but important examples of forcings F(t) with different time variations.

Step function forcing

Here we take F to be a step function of time:

F(t) = 0fort ≤ 0, = F

for t > 0, (8.12)

where F

is a constant. It is then easy to show that the temperature response is given by



(t) = S



1 − e

−t/τ



for t > 0, (8.13)

where

S =

(8.14)

is called the climate sensitivity:

it is the asymptotic value approached by the temperature

perturbation T



as t →∞,whenαT



∼ F in equation (8.8). Figure 8.2(a) plots the time

evolution of the step-function forcing and the resulting temperature response. Note that T



Confusingly, α

−1

is also sometimes called the climate sensitivity; we shall avoid this usage.

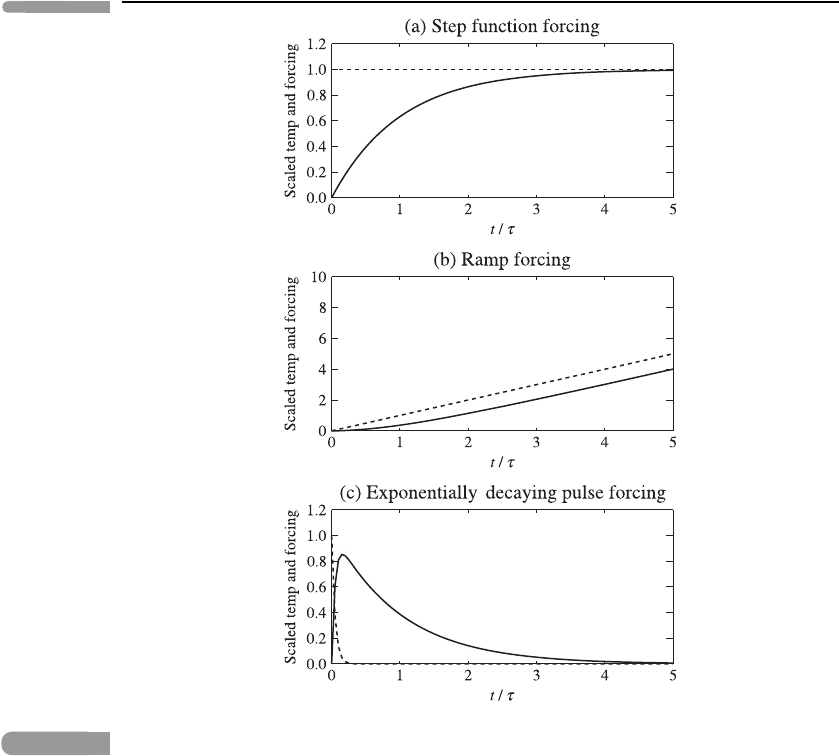
201 Some solutions of the linearised energy balance model

Fig. 8.2

The EBM’s temperature response (solid lines) to three different forcings (dashed lines), plotted

against non-dimensional time t/τ . (a) Response to step function forcing, given by equation (8.12)

with F

> 0; the scaled temperature is T



/S and the scaled forcing is F/F

. (b) Response to ramp

forcing, given by equation (8.15) with γ>0; the scaled temperature is T



α/(γ τ) and the scaled

forcing is F/(γ τ ). (c) Response to exponentially decaying pulse forcing, given by equation (8.17)

with F

> 0andt

= 0.05τ ; the scaled forcing is F/F

, and the scaling of temperature is discussed

in Problem 8.3.

increases linearly, like St/τ ,fort  τ ; its initial slope S/τ = F

/C by equations (8.9)

and (8.14), and hence is independent of the feedback parameter α. However, the feedback

comes into play for t  τ and T



then starts to level off, reaching 0.95S at about t = 3τ .

Ramp forcing

Here the radiative forcing increases linearly with time, for t > 0:

F(t) = 0fort ≤ 0, = γ t for t > 0, (8.15)

202 Climate change

where γ is constant. This is a good representation of the radiative forcing due to increasing

carbon dioxide, since the CO

mixing ratio is currently increasing exponentially in time,

by about 0.5% per year, and the radiative forcing goes roughly like the logarithm of the

mixing ratio: see equation (8.24). In this case the solution is a little more difﬁcult to

obtain, but turns out to be



(t) =

γτ



− 1 + e

−t/τ



for t > 0. (8.16)

Figure 8.2(b) shows the time-development of the forcing and the solution. It can be checked

from equation (8.16) that T



initially (for t  τ ) grows quadratically with time, but later

(for t  τ ) the growth becomes linear with time: this behaviour is clear from the diagram.

Exponentially decaying pulse forcing

Here we take

F(t) = 0fort ≤ 0,

= F

−t/t

for t > 0, (8.17)

where F

and t

are constants. With F

< 0 this might be a representation of the forcing

due to the injection of aerosols into the stratosphere from a massive volcanic eruption.

Figure 8.2(c) shows the time-development of the forcing and the solution for the case

= 0.05τ , corresponding for example to values of t

= 1.5 years and τ = 30 years. Note

that the response is spread over a time scale of order τ , which in this case is much longer

than the time scale t

of the pulse. See also Problem 8.3.

Sinusoidal forcing

Here we take

F(t) = F

sin(ωt) (8.18)

for all t,whereF

is a constant, and seek a purely oscillatory response. This could

approximately represent forcing by the 11-year solar cycle, for example. See Problem 8.4.

Note that the assumption α>0 implies that all of these solutions are stable, in the sense

that the temperature response cannot grow faster than the forcing. It can easily be checked

that if α<0 the solutions will grow exponentially with time, leading to unstable climate

change in the EBM.

8.3.1 Response to forcing that initially increases linearly with time

and then becomes constant

To introduce some of the issues that arise in detailed climate-change modelling, we now

consider the response to ‘ramp-ﬂat’ forcing, which starts as a linear growth with time and

then becomes steady at a speciﬁed time t

, say: this could correspond to increasing CO

203 Some solutions of the linearised energy balance model

forcing for time t

followed by a stabilised CO

amount. The solution is equivalent to a

positive ramp followed by an equal and opposite negative ramp, and can be written



(t) =

γτ



− 1 + e

−t/τ



for 0 < t ≤ t

γτ



− e

−(t−t

)/τ

+ e

−t/τ



for t ≥ t

. (8.19)

Equation (8.19) implies that as t →∞(or more precisely for t − t

 τ ), the temperature

deviation tends to an ‘equilibrium’ value:



(t) → T

eqm

≡

γ t

. (8.20)

This equilibrium temperature perturbation equals the forcing at time t

, F(t

) = γ t

divided by α: this is analogous to the deﬁnition of climate sensitivity in equation (8.14).

Moreover T



approaches T

eqm

from below, so T

eqm

is an upper bound on the temperature

in this model.

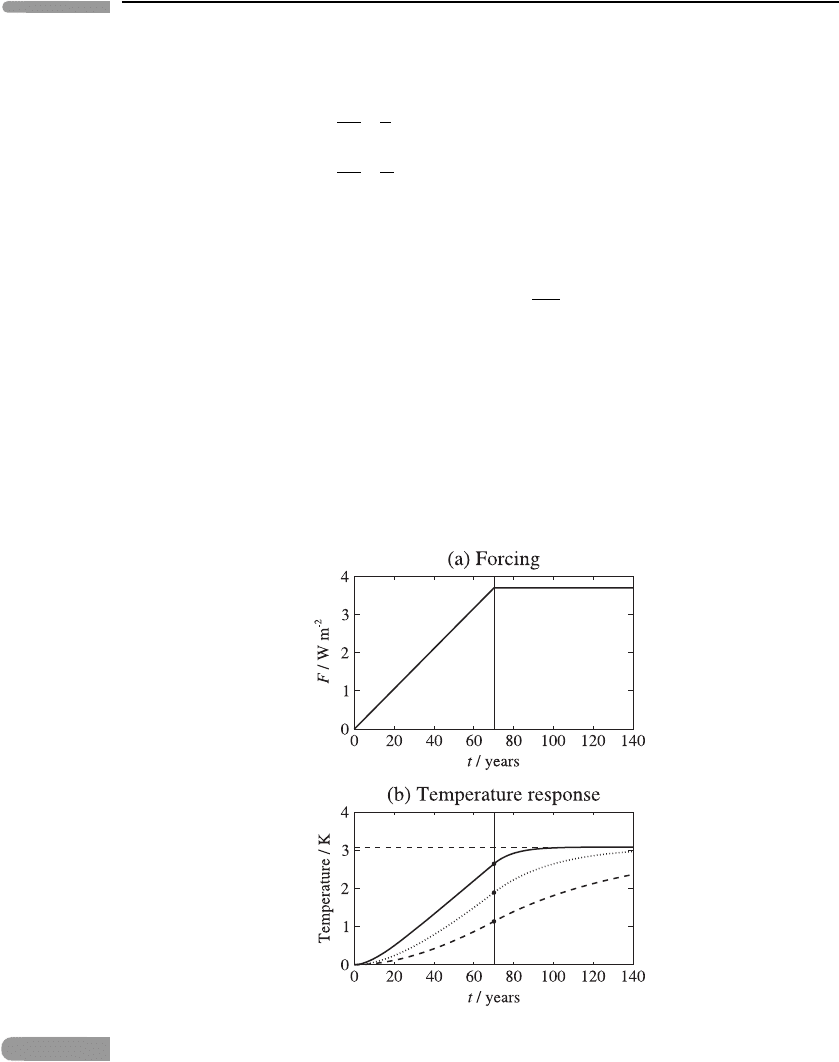
Figure 8.3(a) shows an example of the forcing as a function of time, with t

= 70 years

and γ t

= 3.7 W m

−2

. Figure 8.3(b) shows the corresponding temperature response for

three different values of τ . Note that when τ is much less than t

(solid curve), the response

Fig. 8.3

Time dependence of the temperature response in the EBM to ‘ramp-ﬂat’ forcing, with the

feedback parameter α = 1.2 W m

−2

−1

.(a)Theforcingasafunctionoftime,witht

= 70 years

and γ t

= 3.7 W m

−2

. (b) The temperature response for τ = 10 years (solid), 30 years (dotted)

and 70 years (dashed); these correspond to three different values of C,byequation (8.9),sinceα

is speciﬁed. The thin horizontal dashed line shows T

eqm

, the thin vertical line shows time t

and

the black circles show T



204 Climate change

equilibrates fairly soon after time t

; however, when τ = t

(dashed curve), the approach

to equilibrium is very much slower.

An important goal for climate-change modelling is to forecast the equilibrium tempera-

ture that would result from stabilisation of CO

emissions, given information up to some

ﬁnite time, for example the stabilisation time t = t

. This is straightforward in principle

for the ramp-ﬂat model, provided that the parameters are known. However, a practical

difﬁculty for climate modelling is that (as noted in Sections 8.2 and 8.3) the values of the

parameters α and C for the Earth’s climate system cannot be speciﬁed with conﬁdence;

hence the FRT τ is not well constrained. Any theory has to allow for uncertainty in τ ,and

this will lead to uncertainty in the ratio T

eqm



) and hence in the forecast equilibrium

temperature based on the value at time t = t

. Figure 8.3(b) illustrates how this ratio varies

strongly as τ ranges from t

/7tot

; see also Problem 8.6.

8.4 Climate feedbacks

We now look at climate feedbacks in more detail, taking account of the fact that the

temperature dependence of Q = F

↓

− F

↑

comes about partly through the dependence of

Q on a number of variables V

, such as water vapour concentration, clouds, albedo and

tropospheric lapse rate, each of which depends on temperature. The quantity Q can also

depend on a further set of variables U

, such as carbon dioxide concentration, that are

independent of temperature. We therefore replace Q = Q(T , U) by

Q = Q(T, V

(T), V

(T), ..., V

(T), U

, U

, ..., U

). (8.21)

The deﬁnition (8.6) of climate feedback is replaced by

α =−

∂Q

∂T

−



i=1

∂Q

∂V

where the term ∂Q/∂T refers to the partial derivative of Q with respect to the ﬁrst T

argument in equation (8.21), keeping all the V

and U

constant, and all derivatives are

evaluated at the steady state values (T , U

) = (T

, U

jss

). The feedback parameter α may

be separated into its constituent parts,

α =



i=0

where α

≡−

∂Q

∂T

and α

≡−

∂Q

∂V

for i ≥ 1.

It is found that α

is generally larger in magnitude than the other α

. However, some of the

latter may be non-negligible compared with α

. Moreover, some of these – associated for

example with water vapour (see Section 8.4.2) and clouds – may have the opposite sign to

, and hence signiﬁcantly reduce the total α.

With the form of Q given in equation (8.21) we can also deﬁne the radiative forcing

associated with a perturbation U



in the variable U

205 Climate feedbacks

∂Q

∂U



, (8.22)

by analogy with equation (8.7).

8.4.1 Black-body feedback

The simplest example of feedback occurs when the climate system acts as a black body at

unperturbed temperature T

, and modifying effects due to the atmosphere are neglected.

We assume F

↓

= F

≈ 240 W m

−2

, independent of temperature; the Stefan–Boltzmann

law (1.1) gives F

↑

= σ T

,so

Q = F

↓

− F

↑

= F

− σ T

= 0 (8.23)

in the steady state. Hence T

equals the emission temperature T

≈ 255 K, as in

Section 1.3.1.Takingα

=−∂Q/∂T

gives

= 4σ T

= α

≡ 4σ T

≈ 3.8 W m

−2

−1

;

we call α

the black-body feedback. The fact that α

> 0 expresses the physical result

that the power radiated by a black body increases with its temperature.

In the presence of an atmosphere the situation is more complicated. Equation (8.23) can

be replaced by

Q = F

↓

− F

↑

= F

− σ T

= 0

and if we have a functional relation between T

and T

we can write

=−

∂Q

∂T

= 4σ T

A simple model would be to take T

= εT

,whereε<1 is an equivalent emittance for

the atmosphere, assumed independent of temperature. In this case

= 4σ T

1/4

= ε

1/4

An example is the radiative greenhouse model of Section 1.3.2, for which it is found from

equation (1.5) that ε = (1 +T

)/(1 +T

). However, it should be borne in mind that there

may not be any simple relationship between the global-mean values of T

and T

in the

real atmosphere. Detailed general circulation models of the Earth’s climate can be used to

estimate α

by applying height-independent temperature perturbations in the troposphere.

This gives a value of about 3.2 W m

−2

−1

corresponding to ε ≈ 0.5.

8.4.2 Water vapour feedback

Here Q = Q(T, V (T)),whereV(T) is some measure of the water vapour content of the

atmosphere. In our simple zero-dimensional model we could, for example, take V to be the

206 Climate change

saturation mixing ratio at the mean surface pressure p

∗

V(T ) = μ

(T, p

∗

) ≡ μ

∗

(T).

This dependence of Q = F

↓

−F

↑

on water vapour comes mainly from the OLR F

↑

, although

↓

may also depend on water, through its dependence on water-vapour absorption in the

stratosphere and on the albedo, which in turn depends on clouds and ice.

The corresponding feedback parameter is

=−

∂Q

∂μ

∗

dμ

∗

and from the Clausius–Clapeyron equation (2.37),usingμ

∗

(T) = e

(T)/p

∗

from

equation (2.40),wehave

dμ

∗

which is clearly positive. Moreover, ∂Q/∂μ

∗

is also generally positive, since the OLR F

↑

decreases, and hence Q = F

↓

− F

↑

increases, with increasing amount of water vapour;

therefore α

, unlike α

, is negative. This implies that as the Earth warms (for example

as a result of increasing CO

), increasing water vapour amounts contribute a decrease in

OLR and so tend to warm the climate further.

This is an example of positive feedback.

There is some ambiguity in the climate-change literature over the deﬁnitions of ‘positive’

and ‘negative’ feedback, and even in the deﬁnition of ‘feedback’ itself. The convention we

have used here is to deﬁne a non-black-body feedback α

as ‘positive’ if α

/α

< 0and

as ‘negative’ if α

/α

> 0. However, an alternative deﬁnition is based on the sign of the

total feedback parameter α; as noted at the end of Section 8.3, our simple EBM is stable if

α>0 and unstable if α<0.

Detailed calculations show that −α

/α

≈ 0.4 under present conditions. While this

implies that water vapour contributes a signiﬁcant positive feedback, it is not sufﬁcient

to make the sum α ≈ α

+ α

negative; hence the climate in this model is stable. If

−α

/α

were to exceed 1, an unstable ‘runaway climate’ could develop; however, such

a possibility seems to require conditions that are far warmer than those encountered in

the present-day global-mean terrestrial climate. It has, however, been speculated that this

runaway greenhouse effect may have occurred on the planet Venus.

8.4.3 Other feedback processes

The net inward heat ﬂux Q can depend on temperature in many other ways, and for each of

these we can deﬁne a climate feedback. Examples include feedback processes associated

with clouds, lapse rate, ice-albedo (see Problem 8.7), the carbon cycle, ocean circulation,

etc. Some of these are highly complex and are poorly understood at present: much current

However, it should be noted that the calculation used here is grossly over-simpliﬁed: the real atmosphere is not

at a uniform temperature, and we should really be considering an ensemble of air-parcel trajectories, with each

parcel retaining its mixing ratio until saturated. See Pierrehumbert et al. (2007).

207 The radiative forcing due to an increase in carbon dioxide

research is devoted to trying to understand and quantify the effects of these feedbacks on

climate change.

8.5 The radiative forcing due to an increase in carbon dioxide

Detailed calculations show that the radiative forcing due to a change of CO

is approxi-

mately proportional to the logarithm of the fractional change of CO

mixing ratio: if the

amount increases by a factor β, the radiative forcing is given to a good approximation

β×CO

= 5.3 ln β Wm

−2

. (8.24)

In this section we give a simple, approximate, demonstration of the main physical princi-

ples that underlie this logarithmic dependence. We ﬁnd that the spectral variation of the

transmittance of CO

is an essential feature: a ‘grey gas’ model would fail completely.

The simplest relevant model takes the ground to be a black body at a ‘warm’ temperature

, with Planck function B

νg

≡ B

) (see equation (3.1)) at frequency ν, and represents

the troposphere by a thin slab at a uniform ‘cool’ temperature T

< T

, with Planck function

νt

< B

νg

and spectral transmittance T

. The upward spectral irradiance at frequency ν

above the troposphere is given by emission from the ground (with emittance 1), decreased

by the tropospheric transmittance, plus emission from the troposphere (with emittance

1 − T

↑

= πT

νg

+ π(1 − T

νt

. (8.25)

(Note the analogy with the ﬁrst line of equation (7.3) for the radiance received along a

single path through the whole depth of the atmosphere.) We refer to the upward spectral

irradiance as the spectral outgoing long-wave radiation, or SOLR for short.

The minimum possible value of T

is 0, corresponding to a totally opaque troposphere;

in this case F

↑

equals the black-body irradiance πB

νt

from the (top of) the troposphere.

The maximum possible value of T

is 1, corresponding to a totally transparent troposphere,

when F

↑

equals the surface black-body irradiance πB

νg

. For 0 < T

< 1, equation (8.25)

shows that F

↑

lies between these two extreme values.

For a single absorbing gas the tropospheric transmittance T

can be approximated by

equation (3.23) modiﬁed by the diffusivity factor (see equation (3.16)):

= exp



−1.66



(z)ρ

(z) dz



. (8.26)

Here the integral is taken over the depth of the troposphere, k

is the spectral absorption

coefﬁcient and ρ

is the absorber density.

We wish to ﬁnd the radiative forcing due to a change in density of this absorber. Neglect-

ing any short-wave absorption, this radiative forcing is minus the change of SOLR just

above the troposphere, integrated over all frequencies. Let us suppose that the absorber

density increases by a factor β>1 at each level z, from ρ

(z) to βρ

(z). Equation (8.26)

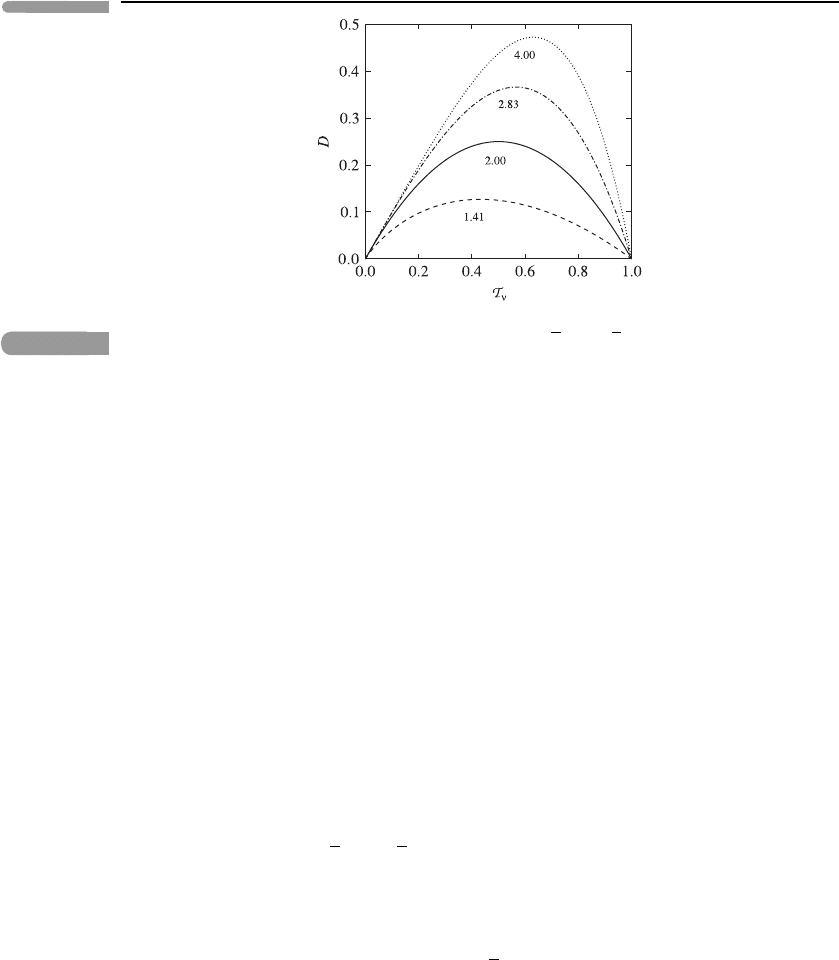
208 Climate change

Fig. 8.4

Plots of D(T

) against T

for β =

√

2, 2, 2

√

2and4.

shows that, under this change, the tropospheric transmittance is raised to the power β,i.e.it

goes from T

to T

. In accordance with the deﬁnition of radiative forcing (see Section 8.1),

we assume that the temperatures of the ground and troposphere do not change under this

absorber change; the resulting change F

↑

in SOLR above the troposphere is therefore

F

↑

= π



νg

− B

νt



T

. (8.27)

Here we have deﬁned the change of tropospheric transmittance

T

≡ T

− T

≡−D(T

, β), say. (8.28)

For β>1and0< T

< 1 this change of transmittance is negative, and D is positive:

hence equation (8.27) implies that the upward irradiance at the tropopause decreases under

the increase of absorber. Alternatively, in terms of equation (8.25), as the transmittance

decreases less SOLR comes from the warm surface and more from the cool troposphere,

leading to an overall decrease of the SOLR. However, D = 0whenT

= 0 or 1, reﬂecting

the fact that the transmittance cannot change at frequencies where the troposphere is already

totally opaque or totally transparent.

Figure 8.4 shows the decrease in transmittance D(T

, β) for the full range 0 ≤ T

≤ 1,

for the four values β =

√

2, 2, 2

√

2 and 4. Note that D attains a maximum value D

max

(β)

somewhere in mid-range, with D

max

increasing with β. It can be shown that, for 1 <β≤ 4,

max

(β) is given to a good approximation by

max

ln β. (8.29)

(See Problem 8.8.)

The value of T

at each frequency ν, and hence the SOLR and the radiative forcing,

for a particular absorbing gas will depend on the amount of absorber and its spectroscopic

properties. We take the absorber to be carbon dioxide and concentrate on its main absorption

band: Figure 8.5(a) plots T

against ν at high resolution and Figure 8.5(b) plots a smoothed

version of T

(cf. Figure 3.14, which includes a low-resolution plot of the transmittance

of a vertical atmospheric column, plotted against wavelength). Focusing for clarity on the