Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 2

Подождите немного. Документ загружается.

341

Для этого можно использовать стандартные программы

ЭЦВМ для вычисления собственных чисел матрицы. Однако

для установления факта асимптотической устойчивости дос-

таточно выяснить знак Re 

. Для этого, как известно [546],

существуют методы установления принадлежности собствен-

ных чисел матриц к левой полуплоскости без вычисления их

значений.

12.3.5.2. Принцип построения матричных критериев

устойчивости

Пусть на плоскости комплексной переменной



задана

некоторая область

[285]. Обозначим

— совокупность

всех матриц порядка

, все собственные значения которых

располагаются внутри области

;



— совокупность всех

матриц порядка

, все собственные значения которых лежат

внутри единичного круга с центром в начале координат на

плоскости комплексной переменной



. Предположим, что

существует оператор

, устанавливающий взаимно-

однозначное соответствие двух множеств:



. Тогда,

если

A A



, то оператор

от матрицы

есть такая матри-

ца порядка

, что





H A B





, и, наоборот, если

есть мат-

рица из семейства



, то





H B A





. Здесь через

1

обо-

значен оператор, обратный оператору

. Для того чтобы

матрица

принадлежала области



, необходимо и доста-

точно, чтобы выполнялось условие





lim

0 .

Покажем это на примере диагональной матрицы. Действи-

тельно, если

чисто диагональная матрица, то по главной

диагонали расположены ее собственные числа   

1 2

, , ...,

Отсюда следует, что условие





lim

0 возможно в том и

342

только в том случае, когда 

 0 для всех

i n

 1 2, , ..., , ибо

есть чисто диагональная матрица, на главной диагонали

которой располагаются числа   

1 2

, , ...,

. Отсюда следует

следующее утверждение: для того чтобы матрица

принад-

лежала области

, необходимо и достаточно, чтобы выпол-

нялось условие

 









lim

H A

0 .

Изложенный принцип далее используется для разработки

алгоритмов устойчивости линейных систем большой размер-

ности, в частности систем электроприводов с вентильным

двигателем.

12.3.5.3. Построение критерия устойчивости

Рассмотрим систему дифференциальных уравнений



АX



, (12.28)

где

— матрица коэффициентов системы, непрерывно зави-

сящих от параметров автоматической системы (коэффи-

циенты усиления, постоянные времени, жесткости, мо-

менты инерции и т.д.);

— вектор-столбец координат.

Чтобы система (12.28) была асимптотически устойчива,

необходимо и достаточно, чтобы все собственные значения



исходной матрицы

лежали в левой полуплоскости ком-

плексной переменной



, т.е. необходимо и достаточно, что-

бы выполнялось условие Re

 0 для всех



1, 2, ...,

, где

решения алгебраического уравнения

A E

  0 . (12.29)

343

Построим матрицу

В,

используя известное дробно-

линейное преобразование, широко применяемое в теории

аналитических функций











. (12.30)

Оно обладает тем свойством, что мнимая ось, рассматри-

ваемая как окружность бесконечного радиуса, переводится

им в окружность единичного радиуса с центром в начале ко-

ординат. Если комплексная переменная



движется вдоль

мнимой оси, то комплексная переменная



перемещается

вдоль единичной окружности. Так как каждой точке левой

полуплоскости комплексной переменной



соответствует

вполне определенная точка, принадлежащая кругу единично-

го радиуса, и наоборот, то это соответствие однозначно











Подставим значение



из выражения (12.30) в (12.29).

Тогда уравнение (12.29) примет вид

A E











0 . (12.31)

Умножая (12.31) на (

 

  1

) и имея в виду, что

a A aA

 , получим:









A A

    1 1 0

или





    

A E A E

 0 .

Умножим это уравнение на (—1),

344









A E A E

    0 .

Полученное выражение умножаем на

 

A E



1

слева

       

A E A E A E A E

     

 1 1

0 ,

окончательно имеем.

   

A E A E E

   

1

0 . (12.32)

Обозначая в уравнении (12.32) матрицу

   

A E A E

  

1

, получим

M E

  0 .

Матрицу

преобразуем следующим образом:

       

M A E A E A E A E E E

        

 1 1

   





 

      

 

A E A E E E A E

1 1

2 2 .

Легко видеть, что если все собственные значения 

ис-

ходной матрицы коэффициентов

лежат в левой полуплос-

кости комплексной переменной



, то все собственные зна-

чения 

преобразованной матрицы коэффициентов

на-

ходятся внутри круга единичного радиуса, и наоборот, если

хотя бы одно 

окажется в правой полуплоскости, среди 

найдется такое, для которого







 1 .

Известно, что собственные значения матрицы

являют-

ся 

, 

, ..., 

, то собственными значениями матрицы

являются 

, 

, ..., 

. Тогда, если система (12.28)

устойчива, последовательное возведение матрицы

в сте-

пень уменьшает абсолютную величину собственных значений



, ибо все 

лежат внутри единичного круга с центром в

345

начале координат и по модулю меньше единицы. Возведение

матрицы в степень рекомендуется выполнять так, чтобы ка-

ждая последующая матрица являлась квадратом предыдущей,

т.е. по закону

;

2 2

k k

, ... .

В этом случае в оперативном запоминающем устройстве

ЭЦВМ не надо постоянно удерживать матрицу

, т.к. каж-

дый раз используются лишь полученные у нее степени.

12.3.5.4. Оценка устойчивости по следу матрицы М

Возможность оценки устойчивости по следу матрицы

S m







вытекает из того факта, что след



устойчивой сис-

темы стремится к нулю при

 

. Рассмотрим этот вопрос

подробнее. Известно, что след матрицы

представляет

собой сумму всех собственных значений 

, взятых в той же

степени, что и матрица

k k k k



   

    

1 2 3

... .

Вопрос о стремлении матрицы

к нулю при

 

мо-

жет быть решен в общем случае путем изучения следов по-

следовательных степеней, взятых в таком количестве, какой

порядок матрицы

. Однако в некоторых случаях при иссле-

довании реальных автоматических систем матрицу

можно

не возводить в степень. Эти случаи выделяет следующая тео-

рема [545].

Если при исследовании системы (12.28) выполняется не-

равенство

S n



 , то среди







, (



1, 2, 3, ...,

) найдет-

ся хотя бы одно, для которого удовлетворяется условие







 1 .

346

Доказательство. Это утверждение легко доказывается от про-

тивного: Допустим, напротив, что все







 1 . Тогда

 









. (12.33)

Но по условию справедливо неравенство

 

S n























. (12.34)

Тогда из неравенства

 

 

i i



















, а также из неравен-

ства (12.33) следует, что





















. (12.35)

Из противоречия неравенств (12.34) и (12.35) непосредст-

венно следует истинность сформулированного утверждения.

Таким образом, если модуль суммы диагональных элементов

превышает порядок матрицы

, .то среди







всегда най-

дется такое, для которого







 1 .

Из рассмотренного неравенства





S n



 вытекает, что

достаточно построить матрицу

и если ее след по модулю

превышает порядок матрицы

, то исследуемая точка про-

странства допустимых значений параметров не принадлежит

области асимптотической устойчивости. Однако если соот-

ношение





S n



 не удовлетворяется, никаких выводов

относительно неустойчивости сделать нельзя. В этом случае

следует рассмотреть следы последовательных степеней мат-

рицы

















S S S S

   

M M M M

; ; , ...

2 4

Для оценки устойчивости достаточно опираться на изучение

следов трех последовательных степеней. Если начиная с не-

которого

следы трех последовательных степеней матрицы

347

убывают, исследуемая система рассматривается как ус-

тойчивая.

Для вычисления элементов матриц

исследуемой сис-

темы необходимо для невозмущенного движения, задавать ди-

намические параметры, приведенные в приложении 12.3.1.

Исследования стационарных режимов и устойчивости

движения системы в целом выполнены на ЭЦВМ по блок-

схеме, приведенной на рис. 12.6. в приложении 12.3.2. Рас-

четные характеристики даны на рис. 12.7. Анализ этих дан-

ных позволяет делать следующие выводы:

1. Система уравнений (12.15) с учетом обозначений





R x





F x







является наиболее полной системой

дифференциальных уравнений исследуемого электропривода

с вентильным двигателем, позволяющая учитывать влияние

конечной жесткости вала привода, различного характера на-

грузки, а также нелинейность характеристик холостого хода.

При необходимости угол нагрузки



и угол коммутации вен-

тилей инвертора



могут быть определены равенствами

(12.20).

2. Множество возможных стационарных движений может

быть определено равенствами (12.18)—(12.21).

3. Приведенная методика исследования устойчивости ста-

ционарных движений на основе матричного критерия Зу-

бова В.И. позволяет построить области допустимых измене-

ний параметров управления САР, что является важным мо-

ментом задач анализа и синтеза систем с ВД.

Приложение 12.3.1

Исходные переменные и параметры системы электропривода

Двигатель серии СТД 4000 2РУ;

 4000 кВт;

 4580 кВА;

cos ,

 0 9 (опережающий);

 6000 В;

 439 А;

 102 В;

 283 А; к.п.д.  97 5, ; Маховой момент ро-

тора —

2 2

278 кг м ; Максимальный вращающий мо-

348

мент при к.з. (при пуске)

макс.

 10 Мном. Частота враще-

ния

 3000 об/мин; Критическая частота вращения

кр

 2230 об/мин;





Нм.

Расчетные параметры в о.е.

 1 655, ;  

0 03, ;  

0 0014, ;  

0 465, ;

 3



;

 1 722, ;



 0129, ;

 1 851, ;

 

014286, ;  

014286, ;

 0 00899, ;

 3 602, ;

 0 01, ;

 1 0, ;

01 , ;

 

 







4 3

sin ;

 10

;



 



11 10

;

  1 0 1 2, , , ; 

 0 0004, ;

L L r r

kd kq kd kq

    0;

Коэффициент приведения роторного тока

mW K K

W K

W ad

f f

пр

, . 

1 4

1 1



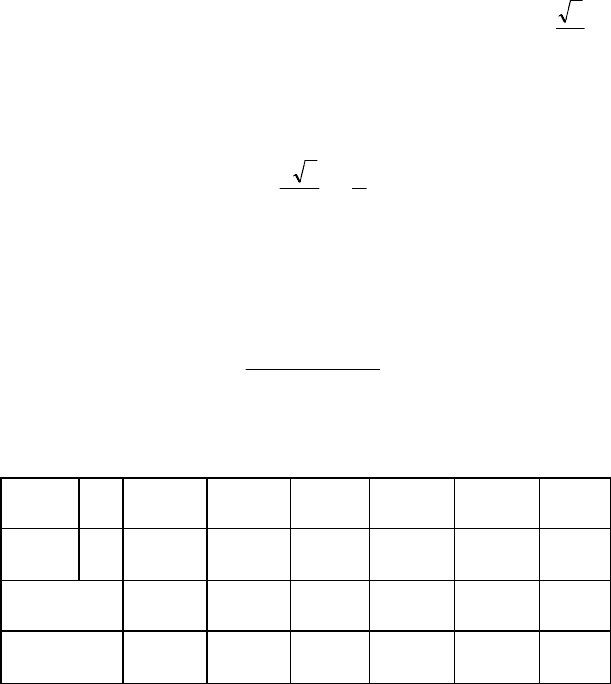
Характеристика холостого хода двигателя



о.

е.

0 0,367 0,581 0,742

0,916 1,115 1,24

,о. е.

0 0,165 0,252 0,33 0,417 0,563 0,709



о.

е.

1,364 1,427 1,497

1,554 1,618

,о. е.

0,913 1,049 1,233

1,417 1,68

349

Функция аппроксимации характеристики





F x x x x x

10 10

1 3532 7 5178 15 8769 15 24140    , , , ,

  3 21016 1 72189 0 00164

, , , .

x x

Приложение 12.3.2

Описание блок-схемы решения задачи

Блок 1. Ввод исходных данных с ПК.

Блок 2. Проверка. Если все заданные варианты просчита-

ны, то передача управления на завершение работы

программы. В противном случае переход к блоку 3.

Блок 3. Для выбранного варианта решение системы нели-

нейных алгебраических и трансцендентных урав-

нений методом Стеффенсена (стандартная про-

грамма

DSNES

) для определения параметров не-

возмущенного движения



Блок 4. Формирование матриц

Блок 5. Вычисление матрицы

Блок 6. Вычисление матрицы

Блок 7. Вычисление следа матрицы





M M





Блок 8. Проверка. Если







 8 то переход к блоку 11.

В противном случае — к блоку 9.

Блок 9. Вычисление













S S S

  

M M M

2 4 8

, , .

Блок 10. Выдача на печать результатов решения программы.

Переход к блоку 2.

Блок 11. Выдача на печать сообщения "Система неустойчи-

ва". Переход к блоку 2.

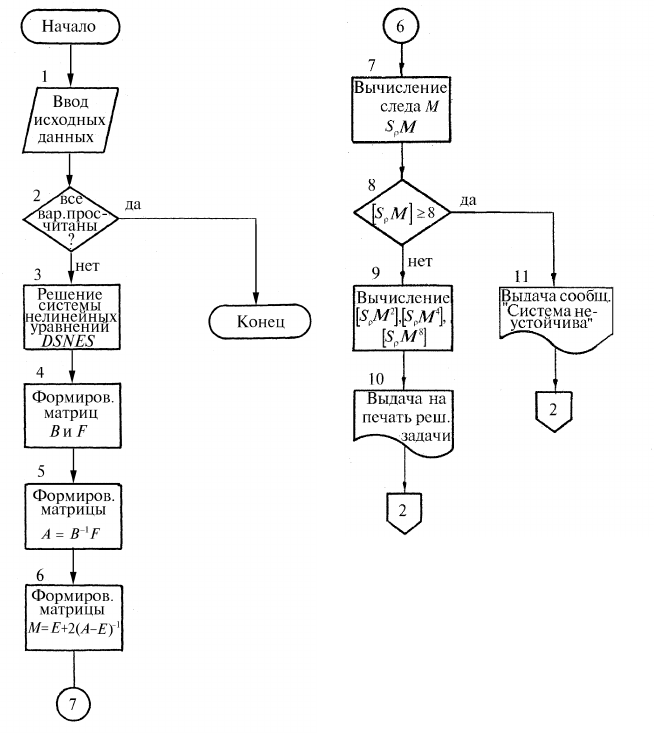
350

Рис. 12.6. Блок-схема решения задачи