Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 2

331

ных трансцендентных уравнений для определения парамет-

ров

x

i

0

. При этом учитываем, что

dx

d

i

0



 .

Получим:

 

 

 

 

 

   

 

  

     

   



     

 

   

  



U r x

K U R R x U

L L x x x L x x

r x x

K U R R x U

L x x

L L x x x r x x

F x L x r

f f

cx a

aq q aq

cx a

ad

ad d

ad kd

10

1

20

60

30

60

50

20 30

1

20

60

40

20

60

30 20 30

10 60

0 2

0

;

sin cos

cos

sin ;

cos cos

sin cos

;

 

 

 

   



п э д

к

п э д

к



 



 

     



 

 

x r x

cx L L x x

L x x x

L x x x F x L x x

cx M M x x M x

kq

ad aq

aq

ad ad

c

40 50

10

2

20

2

30

50

20 30

40

20 30 10 20 30

70 0

60

80 0 80

0

1

2

0 0

; ;

sin

cos cos ;

; ,

 

    

 

 

     











 

   



(12.17)

где

 

R L L x

F x

x

x a x a x a x a

d q

x

n n

э

 













 















    















3

1 3

2

60

10

0

10 0 10 1 10

1

10



 







sin ;

;

... .



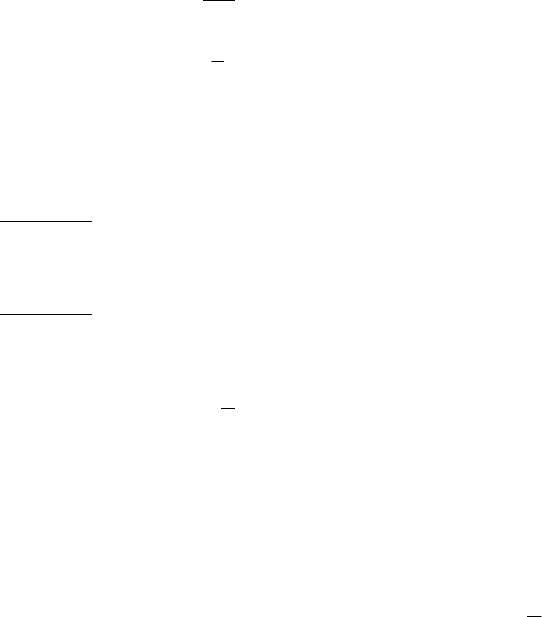
332

Анализ системы (12.17) позволяет определить некоторые

x

i

0

, а именно:

 

 

x

U

r

x x x

x

c

M M x M

f

c

10 40 50 80

70 0

60

0

0 0 0

1





  

  











; ; ; ;

.



(12.18)

Для определения

x

20

,

x

30

и

x

40

с учетом (12.18) имеем

систему нелинейных трансцендентных уравнений

 

 

 

 

 

   

 

   

sin

cos

cos sin ;

cos

sin cos ;

sin





 





 





K

U R R x U L L

x x x r x x

K

U R R x U L L

x x x r x x F x L x

M M M x L L x x

F x L

cx

a aq q

cx

a ad d

ad

c ad aq

ad

1

20

60

30 20 30

1

20

60

30 20 30 10

60

0 0

60

2

20

2

30

10

2

1

2

п э д к

     

 

      

  

     





x x

20 30

cos .











(12.1

9)

Для однозначного решения систем (12.18) и (12.19) необ-

ходимо задавать следующие параметры электропривода (см.

приложение 12.3).



U

f

, 

r

f

,



,

K

cx

, cos

1

,

U

п

,

R

д

,

L

д

,





  , sin

2



,



L

d

, 

L

q

, 

U

a

,

r

,

L

ad

,

L

aq

,

L



,





F x

10

,

с

,

M

c

.

Задачу определения установившихся режимов можно не-

сколько расширить, если ввести дополнительные выражения

для определения угла нагрузки



и угла коммутации венти-

лей инвертора



[13]:

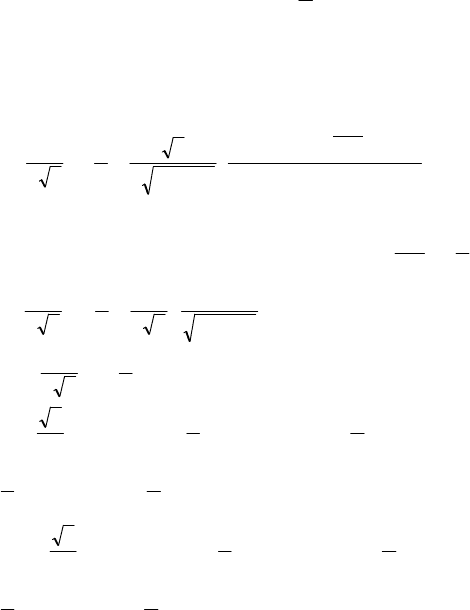
333

x

b b b

30 1

0

2

1 2

2

0

  

  











 



 

;

,

(12.20)

где

   

 

 

b

L L

L x

r

x

L x L x

r

x

b

L

L L

f x f x

b

f

d q

q

d q

d

d q

q d

d

0

30

60

30

1

30 1 30 1

60

1 0 30 0 30

2

0 1

4 3

2

3

4

2

2 3

2

4 3

2 3

2

3

4

1

4

2

 

  









      







  

  



  

   

 



 



  

 



sin

cos sin

sin

sin sin cos cos sin ;

cos sin cos ;

sin ;

sin sin



 



 

   









 







1 1

1

0 1 1 1

1

2

6

1

2

3 3

3

4

1

4

2 2

6

1

2

3 3

3

12 21

 

























  

  













       

























 

  























 



  



cos

cos ;

cos sin sin

sin

( . )

f

q

Таким образом, по уравнениям.(12.19), (12.20) с учетом

обозначений по (12.21) можно определить

x

20

;

x

30

;

x

60

;



и



.

Далее по выражению (12.18) определяется значение

x

70

.

Для этого необходимо задать значения параметров электро-

привода, приведенные в приложении, за исключением



и



.

334

Полученная методика является наиболее общей из из-

вестных и позволяет найти множество установившихся ре-

жимов типа

x

i

0

 const , см. расчетные характеристики рис.

12.7.

12.3.4. Уравнения возмущенного движения

Для получения уравнений возмущенного движения в вы-

ражения (12.15) подставим

x x x

i i

 

0 1

~

, (12.22)

где

~

x

i

— малые отклонения (возмущения) от соответствую-

щих установившихся значений

x

i

0

 const .

Учитывая

x

i

0

 const , получим:









       

 



























U r x r x L x x L x x x

L L

F

x

x L x

f f f ad ad

f ad ad

10 1 30 2 30 20 3

1

0

1 4

~

sin

~



cos

~



~



~



;

   





 

  













  

L

K

L L x x L L x

cx

ad d ad d

д

к к

cos

sin

~







   

 

1

30 2 20



 













   cos

~



~



~



sin

cos

x x L

F

x

x L x

K

U

ad ad

cx

30 3

1

0

1 4

1



 



п











 

        

R R x U R R x Rx L L

a ad d

э д э д к20 2 20

2



~



 





    

x x x x x x x x x x x x x

20

60

30 20

60

30 3 20 30

6 60

30 2

cos sin

~

cos

~

cos

~





    

L x x L x x L x x r x x x

aq aq aq

60

50

60

5 50

6

20 30 3

~ ~

cos

~

 









 

r x x r x x

   

20 30 30 2

sin sin

~

;

 

  













  

L

K

L L x x L L x

cx

aq q aq q

д

к к

cos

~







   

 

1

30 2 20

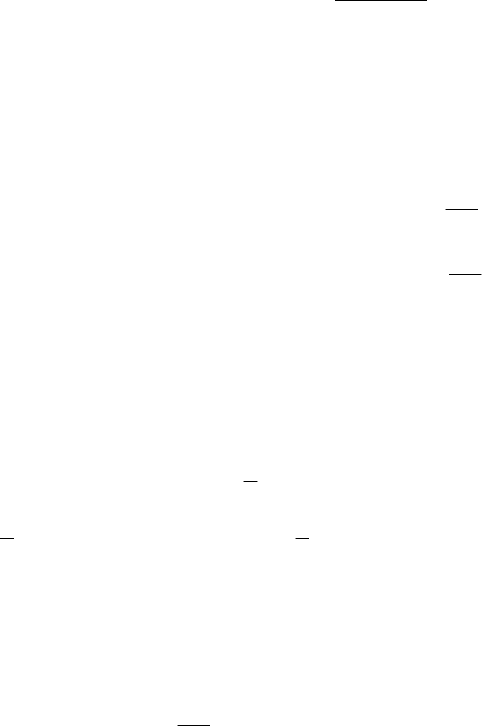
335

    sin

~



~



cos

x x L x

K

aq

cx

30 3 5

1

















 

         

U R R x U R R x Rx L L

a ad d

п э д э д к20 2 20

2

~



 

















     

x x x L L x x x x L L

ad d ad d

20

60

30 20

60

30 3

sin cos

~

 

   

к к









    

x x x L L x x x L x x

ad d ad

20 30

6 60

30 2

60

40

sin

~

cos

~



 

к









    

L x x L x x r x x r x x x

ad ad

60

4 40

6

20 30 20 30 3

~ ~

cos sin

~

   

     

   













r x x F x L x F x L x

F

x

L x x

ad ad ad

 



cos

~ ~ ~

;

30 2 10

60

10

6

1

0

60

1

   

L x x L x x x L

F

x

ad ad ad

   



sin

~



cos

~



~

30 2 20 30 3

1

0

1

 



















      

L L x r x r x

ad kd kd kd



~



~

;

4 40 4













    

L x x L x x x L L x

aq aq ad kd

   



cos

~



cos

~



~



30 2 20 30 3 5

    

r x r x

kq kq

50 5

~

;





 

J x cx cx L L x x

ad aq

1

6

70 7

2

20

2

30

1

2

~ ~

sin    







 





 





 

    

1

2

1

2

20

2 2

30 3

2

20

2 2

30 3

L L x x x L L x x x

ad aq ad aq

   sin

~

cos

~













   

L L x x x L x x x

ad aq aq

   

2

20 30 2 20 30 5

2sin

~

sin

~













  

L x x x F x L x x

ad ad

   

20 30 4 10 20 30

cos

~

cos

















  

F x L x x F x L x x x

ad ad

10 30 2 10 2 3 3

   cos

~

sin

~

 























 

F

x

L x x x

ad

1

0

20 30 1

cos

~

;























J x x c x x M M x x M M

c c

2 8

6

70 7 0

60

80 0

~



~



~

        











   









x x x x M

60

80

1

6

8 0



~ ~

;

~



~

.

x x x

7 80 8

  (12.23)

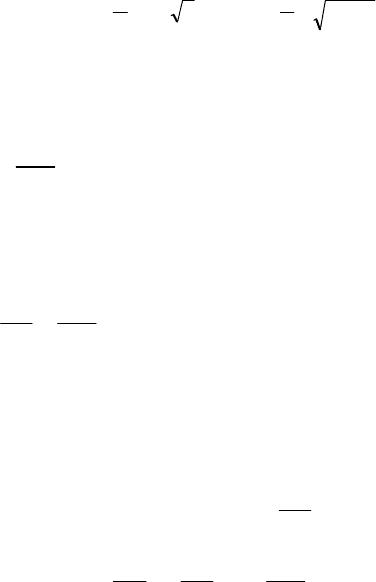
336

Во втором и третьем уравнениях системы (12.23) приве-

денное сопротивление принимает значение

 

~

sin

~

.

R L L x

d q

 

























 

3

1 3

2

6



 



В системе уравнений (12.23) учтена нелинейная аппрок-

симирующая функция

       

F x

a

a x x a x x a x x

n

n n n

1

0 10 1 1 10 1

1

2 10 1

2

1

       









 

~ ~ ~

...





  









a x x a

n

1 10 1

2

~

и ее производная

 



F

x a

a n x x a n x x

n

n n

1 1

0 10 1

1

1 10 1

2

1

1     









 

~ ~

 





    









a n x x a

n

2 10 1

3

1

2

~

... ,

которые согласно формуле бинома Ньютона могут быть

представлены в виде

   

F x F x

F

x

F

x

F

x

F

x

1 1 10

1

0

1

1 1

0

2

1

2

0

1

 





















































~

;

.

(12.24)

Заметим здесь же, что





sin

~

sin cos

~

x x x x x

30 3 30 30 3

   и





cos

~

cos sin

~

x x x x x

30 3 30 30 3

   .

337

Члены системы (12.23), содержащие

~

x

i

в первой степени

— определяют возмущенное движение, а все остальные чле-

ны — невозмущенное движение (установившейся режим) и в

уравнениях указанной системы они составляют тождества.

В силу вышеизложенного и опуская для простоты записи

волнистые черточки над переменными

x

i

, получим уравне-

ние возмущенного движения в матричной форме:

B

X

FX





, (12.25)

где матрицы

B

и

F

имеют вид

B















b b b b

b b b

b b b b

b b b

b

b b

b

11 12 13 14

21 22 23 24

32 33 35

41 42 43 44

52 53 55

66

76

78

87

0 0 0 0

0 0 0 0 0

0 0 0 0

0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0

0 0 0 0 0 0 0

;

F















f

f f f f

f f f f f

f

f f f f f f

f f f

f

11

22 23 25

26

31 32 33 34

36

44

55

61 62 63 64 65 67

76

77 78

88

0 0 0 0 0 0 0

0 0 0 0

0 0 0

0 0 0 0 0 0 0

0 0

0 0 0 0 0

0 0 0 0 0 0 0

.

В векторном уравнении (12.25)

 

X



x x x

T

1 1 8

, , ..., — мат-

рица-столбец размерности 1



8.

338

Коэффициенты

b

ij

матрицы

B

в (12.25) определяются

нижеследующими соотношениями:

b L L

F

x

f ad

11

1

0

 

















;





b L x

ad

12 30

    sin ;





b L x x

ad

13 20 30

    cos ;

b L

ad

14

  ;

b L

F

x

ad

21

1

0

















;













b L K L L x

cx ad d

22 1

1

30

   















д к

cos cos sin ;   







b L L x x

ad d

23 20 30

  

к

cos ;

b L

ad

24

  ;













b L K L L x

cx aq q

32 1

1

30

   















д к

cos cos cos ;   











b L L x x

aq q

33 20 30

 



 

к

sin ;

b L

aq

35

 ;

b L

F

x

aq

41

1

0

 















;





b L x x

aq

42 20 30

   cos ;





b L L

ad kd

44

 



;





b L x

aq

52 30

    cos ;





b L x x

aq

53 20 30

   sin ;

b L L

aq kq

55

 



;

b J

66 1

 ;

b J

76 2

 ;

b J

78 2

 ;

b

87

1 .

Элементами матрицы

F

ij

по (12.25) будут:

f r

f

11

  ;

 





 

f K R R r x

cx

22 1

1

30

   



sin cos sin   

э д









 

L L x x

aq q



 

к

60

30

cos ;

339













f L L x x x r x x

aq q

23 20

60

30 20 30

   



   

к

sin cos ;

f L x

aq

25

60

  ;





   

f L L x x K

aq q cx

26

20 30 1

1

   





   

к

cos sin cos

 

 

























 

x L L

d q

20

2

3

1 3

2

 



sin ;

f

F

x

L x

ad

31

1

0

60

















;

 





 

f K R R L L x x

cx ad d

32 1

1

60

30

    



cos cos sin   

э д к







r x

  cos ;

30













f L L x x x r x x

ad d

33 20

60

30 20 30

   



   

к

cos cos ;

f L x

ad

34 60

  ;

 

f K x L L

cx d q

36 1

1

20

2

3

1 3

2

 

























  



cos cos sin 



 















  

L L x x F x L

ad d ad



 

к 20 30 10

sin ;

f r

kd

44

   ;

f r

kq

55

   ;

 

f

F

x

L x x

ad

61

1

0

20 30

















  cos ;





 

f L L x x F x L x

ad aq ad

62

2

20 30 10 30

1

2

2      sin cos ;

















f L L x x L L x x

ad aq ad aq

63

2

20

2 2

30

2

20

2 2

30

       sin cos











F x L x x

ad

10 20 30

  sin ;

340





f L x x

ad

64 20 30

   cos ;





f L x x

aq

65 20 30

   sin ;

f c

67

  ;









f M M x x

c

76

0

60

80

1

   





;

f c

77

 ;









f M M x x

c

78 0

60

80

1

   





;

f

87

1 ;

f

88

1 .

Уравнения возмущенного движения в виде (12.25) не-

удобны для проведения исследований устойчивости невоз-

мущенного движения (12.16). В практике исследований

обычно систему (12.25) приводят к форме Коши. Процедура

приведения уравнения (12.25) к форме Коши формально ре-

шается следующим образом.

Умножим слева уравнение (12.25) на обратную матрицу

B

1

:

B

X

B

FX

 



1 1



.

Очевидно

B

E





1

, где

Е

— единичная матрица размер-

ности 8



8. Тогда

E

X

AX





, (12.26)

где

A

B

F



1

.

В результате преобразований система (12.25) приводится

к форме Коши (12.26).

12.3.5.1. Матричный критерий устойчивости

Известно [542, 545, 546], что если в (12.25) и (12.26)

все





Re , , ...,

i

 0 1 2 8 , то нулевое решение системы

(12.26) асимптотически устойчиво по Ляпунову. Таким обра-

зом, для исследования асимптотической устойчивости авто-

номной системы возникает задача определения знаков кор-

ней характеристического уравнения



E A

  0 . (12.27)

Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 2

Подождите немного. Документ загружается.