Аскирка В.Ф. Электричество и магнетизм. Волновая оптика

Подождите немного. Документ загружается.

101

Величина dnlN 1== фактически представляет собой число

витков, приходящихся на единицу длины тороида (соленоида).

Между напряженностью и индукцией магнитного поля в

ферромагнетике имеется зависимость [11.5]:

mm= , (3)

где магнитная проницаемость

может быть определена по гра-

фику зависимости

(

)

HfB = , приведенному в приложении 12.

Для определения величины магнитного поля в сердечнике

воспользуемся теоремой о циркуляции вектора напряженности

магнитного поля [11.6]:

=×

IldH

. (4)

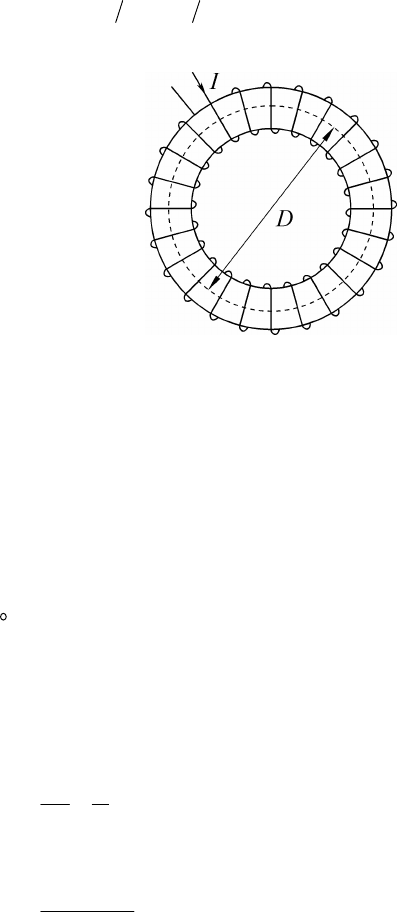
В качестве контура интегрирования целесообразно взять

среднюю линию тороида, длина которой Dl

. В силу сообра-

жений симметрии во всех точках этого контура величина поля

должна быть постоянна ( constH

), поэтому выражение (4) запи-

шется в виде NIHl

, откуда:

H == . (5)

Вычисления по (5) позволяют найти значение напряженности

магнитного поля в стальном сердечнике:

1250

1040,0

50,0

А/м.

Рис. 1.50

102

Величину магнитной индукции в сердечнике определяем по

кривой намагничивания стали (смотри приложение 12):

22,1

B Тл. Выражение (1) с учетом (2) и (3) будет иметь оконча-

тельный вид:

= . (6)

После подстановки числовых значений получим:

()

3,2

12501040,0

22,1100,340,014,3

××

××××

Гн.

Энергия магнитного поля соленоида индуктивностью

, по

обмотке которого течет ток силой

, выражается соотношением

[10.14]:

W = . (7)

Рассчитанная индуктивность позволяет получить значение

энергии магнитного поля тороида:

288,0

50,03,2

=W Дж.

Ответ: 3,2

L Гн, 288

W мДж.

Пример 22. Обмотка тороида с сердечником, в котором име-

ется узкий вакуумный зазор, содержит 1200 витков (рис. 1.51). Си-

ла тока в обмотке составляет 1,0 А. Диаметр тороида по средней

линии равен 32 см. Определить длину вакуумного зазора, при ко-

торой индукция магнитного поля в нем будет равна 0,60 Тл?

Дано:

1200

N ,

0,1

I А,

d см 32,0

м,

60,0

B Тл.

Найти:

l .

103

Решение. Для решения задачи необходимо использовать тео-

рему о циркуляции вектора напряженности магнитного поля

[11.6]:

=×

IldH

. (1)

Выберем замкнутый контур

вдоль средней линии тороида.

Тогда левая часть (1) будет определяться выражением:

(

)

000

HlHldldH

+-p=×

, (2)

где

H – модули вектора напряженности магнитного поля в

сердечнике и зазоре соответственно.

Таким образом, теорема (1) примет вид:

(

)

NIHlHld =+-p

000

. (3)

Пренебрегая рассеянием магнитного потока в области зазора,

учтем, что

BB = , где

B – модули векторов индукции маг-

нитного поля в сердечнике и зазоре соответственно.

Для вакуумного зазора величины индукции и напряженности

магнитного поля связаны соотношением [11.5]:

. (4)

Рис. 1.51

104

Для стального сердечника величину

определим по кривой

намагничения для стали (смотри приложение 12): при

60,0

== BB Тл значение 150

H А/м. Подставив (4) в (3), выра-

жая

l , получим:

(

)

dHNI

Подставляя числовые значения, имеем:

(

)

102,2

1501014,3460,0

15032,014,30,112001014,34

×=

×××-

××-×××

м.

Ответ: 2,2

=l мм.

Пример 23. Конденсатор емкостью 5,0 мкФ, обладающий за-

рядом 0,50 мКл, в начальный момент времени замкнули на рези-

стор. Найти зависимость силы тока в цепи, а также количества те-

плоты, выделившегося на активном сопротивлении, от времени.

Через какой промежуток времени заряд на конденсаторе умень-

шиться в пять раз? Сопротивление резистора принять равным

1,0 кОм.

Дано:

0,5

C мкФ

100,5

×= Ф,

50,0

=q мКл

1050,0

×= Кл,

0,1

R кОм 1000

Ом.

0,5

n .

Найти:

(

)

tfI = ,

(

)

tfQ = , t

Решение. Согласно закону Ома для участка цепи [5.15], в ко-

торую входят резистор и конденсатор:

j-j=iR , (1)

где

j-j – разность потенциалов между обкладками конденса-

тора,

– сила тока.

105

Так как напряжение на конденсаторе [4.10] равно

Cqu =j-j=

, то выражение (1) запишется в виде:

iR = . (2)

Продифференцируем по времени выражение (2), учитывая 0<

di 1

-= . (3)

Сила тока по определению [5.1]:

i = , (4)

поэтому в (3) с учетом (4), разделяя переменные, получим диффе-

ренциальное уравнение вида:

di 1

-= . (5)

Проинтегрируем уравнение (5) по времени от нуля до

, учитывая,

что при этом сила тока изменяется от

I до

òò

RCi

, следовательно,

ln -= , откуда

. (6)

После потенцирования выражение (6) можно записать в виде:

(

)

RCt

eII

. (7)

Из равенства (2) при

qq = имеем

(

)

RCqIi

== . С учетом

этого уравнение (7) примет вид:

()

RCt

Выполнив вычисления, получим:

()

005,0100,51000

10,0

100,51000

1050,0

eeI

-××-

××

Количество теплоты, выделяемое в сопротивлении при

протекании по нему изменяющегося электрического тока,

определяется из закона Джоуля-Ленца [7.1] в дифференциальном

виде:

106

RdtIdQ

= . (8)

Количество теплоты, выделившееся за конечное время

, оп-

ределяется выражением, полученным путем интегрирования вы-

ражения (8):

RdtIQ

. (9)

После подстановки (7) в (9) получим:

() () ()

-===

---

òò

RCt

RIdteRIRdteIQ

()

RCt

-= .

С учетом данных задачи получим:

(

)

()

(

)

()

eeQ

400100,510002

1025,01

100,52

1050,0

-××-

-=-

××

Дж.

За время dt через сопротивление

пройдет заряд (восполь-

зуемся определением силы тока (4) и выражением (7)):

(

)

dteIdq

RCt-

. (10)

Заряд, который прошел за промежуток времени t

, можно опре-

делить путем интегрирования уравнения (10):

()

() ()

()

=-=-==

D-

RCt

eRCIeRCIdteIq 1

(

)

(

)

RCt

D-

-= 1

. (11)

По условию задачи заряд на конденсаторе через некоторый

промежуток времени уменьшается в пять раз, то есть nqq

= ,

тогда выражение (11) можно записать в виде:

(

)

RCt

D-

-=11, (12)

преобразовывая и потенцируя (12), получим искомое выражение

для нахождения промежутка времени:

RCt .

После подстановки числовых значений получим:

107

1012,1

ln100,51000

×=

×××=Dt с.

Ответ:

005,0

10,0

= А,

(

)

400

1025,0

-= Дж, 12,1

t мс.

Пример 24. В замкнутом контуре происходят свободные

электромагнитные колебания. Определить частоту колебаний, ес-

ли максимальный заряд конденсатора 1,0 мкКл, а максимальный

ток в контуре – 10 А. Активное сопротивление контура пренебре-

жимо мало.

Дано:

0,1

=q мкКл

100,1

×= Кл,

=I А.

Найти:

Решение. В колебательном контуре совершаются незатухаю-

щие свободные колебания, так как активным сопротивлением кон-

тура пренебрегаем. В этом случае выполняется закон сохранения

энергии: в любой момент времени энергия контура, определяемая

суммой энергии электрического поля конденсатора и магнитного

поля катушки, остается постоянной. В момент, когда конденсатор

максимально заряжен, сила тока в катушке равна нулю, и, наобо-

рот, когда сила тока в катушке максимальна, – конденсатор пол-

ностью разряжен. Закон сохранения (превращения) энергии будет

иметь вид [4.18], [10.14]:

const

. (1)

Период незатухающих электромагнитных колебаний в конту-

ре определяется формулой Томсона [13.6]:

LCT p= 2. (2)

Из соотношения (1) выразим LC :

LC = . (3)

108

Учитывая связь периода с частотой n=1T [13.27], а также

соотношение (3), выражение (2) можно записать в виде:

2 q

. (4)

Подставляя числовые значения в (4), получим искомое значе-

ние частоты:

106,1

100,114,32

×»

×××

Гц.

Задачу можно также решить, учитывая, что в случае незату-

хающих электромагнитных колебаний контура выражение, опре-

деляющее изменение заряда на конденсаторе с течением времени,

имеет вид [13.2]:

(

)

j+w= tqq

cos , (5)

где

q – начальный максимальный заряд конденсатора,

w – соб-

ственная циклическая частота колебаний контура,

– начальная

фаза колебаний.

По определению сила тока является первой производной за-

ряда по времени:

()

j+ww-== tq

000

sin,

или с учетом тригонометрических соотношений:

(

)

2cos

000

p+j+ww= tqi . (6)

Величина, стоящая перед косинусом – амплитудное значение

силы тока, то есть:

000

Iq =w . (7)

Воспользовавшись соотношением между частотами [13.27]

pn=w 2

выражение (7) преобразуется к виду:

2 q

то есть совпадает с выражением, полученным первым способом.

Ответ: 6,1

МГц.

109

Пример 25. Какую энергию необходимо подвести к колеба-

тельному контуру с малым затуханием с логарифмическим декре-

ментом затухания 0,020, чтобы поддерживать в нем незатухающие

колебания в течение 30 мин, если контур состоит из конденсатора

емкостью 40 нФ и катушки с индуктивностью 5,0 мГн, а макси-

мальное значение силы тока в катушке достигает 6,0 мА?

Дано:

020,0

t мин 180

с,

C нФ

100,4

×= Ф,

0,5

L мГн

100,5

×= Гн,

0,6

=I мА

100,6

×= А.

Найти: W

Решение. Вследствие наличия активного сопротивления ка-

тушки колебания в контуре будут затухающими, то есть амплиту-

да силы тока в катушке со временем будет уменьшаться по экспо-

ненциальному закону:

eII

, (1)

где

– коэффициент затухания.

Так как энергия контура пропорциональна квадрату амплиту-

ды силы тока в катушке индуктивности [10.14], то, используя со-

отношение (1), получим выражение для изменения со временем

энергии контура:

eWW

, (2)

где

W – максимальное значение энергии катушки (контура).

Относительное уменьшение энергии за период с учетом вы-

ражения (2) равно:

eWW

Так как колебания слабозатухающие, то коэффициент затуха-

ния мал, поэтому, воспользовавшись приближенной формулой

110

a+»

1e при 0,1

, а также [13.11], получим окончательное

выражение для относительного изменения энергии контура:

l=b»

. (3)

Для нахождения периода слабозатухающих колебаний можно

воспользоваться формулой Томсона для периода незатухающих

колебаний в электромагнитном контуре [13.6]:

LCT p» 2. (4)

Полная энергия, поддерживаемая в контуре [10.14]:

W = , (5)

Изменение энергии контура за период вследствие потерь (то есть

та энергия, которую нужно подвести извне для поддержания неза-

тухающих колебаний) равно

D , (6)

где W

– изменение энергии контура за время t

С учетом соотношений (4) – (6) выражение (3) запишется в

виде:

l=p

. (7)

После преобразований выражение (7) будет иметь вид:

Подставляя числовые значения, получим:

(

)

103,7

1040

100,5

14,32

180100,6020,0

×=

×××

=DW Дж.

Ответ: 3,7

W мДж.

Пример 26. Определить полное, активное и реактивное со-

противления катушки, ее индуктивность, а также полную и реак-

тивную мощности при прохождении через нее переменного тока,

мгновенное значение силы которого определяется уравнением