Аскирка В.Ф. Электричество и магнетизм. Волновая оптика
Подождите немного. Документ загружается.


81
Пример 11. Нагревательный элемент электрического чайника
имеет две обмотки. Если в сеть включена одна из них, вода в чай-
нике закипает через 12 мин. Если в ту же сеть включена другая –
через 25 мин. Сколько времени необходимо для закипания воды в
чайнике, если включить в сеть две обмотки: параллельно; после-
довательно? КПД чайника постоянен.
Дано:
12
1
=t мин,
25
2
=t мин.
Найти:
посл
t ,
пар
t .
Решение. Учитывая, что во всех случаях чайник включается в
одну и ту же сеть с напряжением U , то для решения воспользуем-
ся законом Джоуля-Ленца [7.1] в форме:
t=
R
U
Q
2
. (1)
Так как количество воды в чайнике, а также его КПД посто-
янны, то для закипания воды во всех случаях требуется одинако-
вое количество теплоты Q
¢
, которое связано с количеством тепло-
ты Q , выделяемым при прохождении электрического тока в об-
мотках, соотношением:
QQ h=
¢
, (2)
где
h
– КПД чайника.
Тогда при включении первой обмотки с сопротивлением
1
R
выражение (1) с учетом (2) примет вид:
1
1
2
th=
¢
R
U
Q
. (3)
При включении второй обмотки получим аналогичное выражение:
2
2
2
th=
¢
R
U
Q
. (4)
При последовательном соединении обмоток общее сопротивление
проводников [5.13]:

82
21
RRR
посл
+= . (5)
Следовательно, выделяющееся при этом количество теплоты
равно:
посл
RR
U
Q t
+
h=
¢
21
2
. (6)
При параллельном соединении обмоток их общее сопротивление
определяется из выражения [5.14]:
21
21
RR
RR
R
пар
+
=
. (7)
Следовательно:
(
)
пар
RR
RRU
Q t
+
h=
¢
21
21
2
. (8)
Выражая из (3) и (4) сопротивления
1
R и
2
R , подставляя сначала в
(6), а затем в (8), получим:
Q
U
Q
U
U
Q
посл
¢
th
+
¢
th
th
=
¢
2
2
1
2
2
, (9)
Q
U
Q
U
Q
U
Q
U
U
Q
пар
¢
th
¢
th
t
÷
÷
ø
ö
ç
ç
è
æ
¢
th
+
¢
th
h
=
¢
2
2
1
2
2
2
1
2
2
. (10)
Из соотношения (9) выражаем искомое время закипания воды при
включении двух обмоток последовательно:
372512
21
=+=t+t=t
посл
мин.
Из соотношения (10) выражаем искомое время закипания воды
при включении двух обмоток параллельно:
0,8
2512
2512
21
21
»
+
×
=
t+t
t
t
=t
пар
мин.
Ответ: 37=t
посл
мин, 0,8=t
пар
мин.
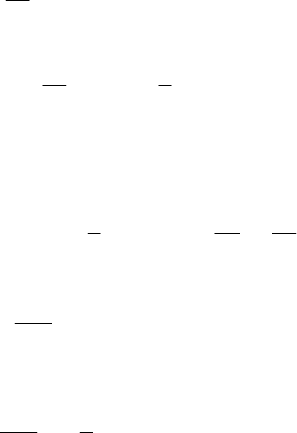
83
Пример 12. Через спираль сопротивлением
R
течет ток, сила
которого уменьшается линейно до нуля в течение времени
t
.
Определить количество теплоты, которое выделится в спирали
при прохождении через нее заряда
0
q .
Дано:
R
,
t
,
0
q .
Найти: Q .
Решение. Сила тока, текущего через сопротивление, линейно
уменьшается со временем до нуля. Соответствующий закон изме-
нения силы тока можно записать в виде:
ktIi -=
0
, (1)
где k – некоторый коэффициент.
Поскольку в конечный момент времени сила тока равна нулю
( 0
=
i ), то t= kI
0
, откуда неизвестный коэффициент k выражает-
ся в виде:
t
=
0
I
k . (2)
С учетом (2) выражение (1) приобретет вид:
÷
ø
ö
ç
è
æ
t
-=
t
-=
t
It
I
Ii 1
0
0
0
. (3)
Заряд, прошедший через спираль за время dt , согласно определе-
нию [5.1] idtdq
=
. Тогда интегральное соотношение для нахожде-
ния всего заряда будет иметь вид:
t=
÷
÷
ø
ö
ç
ç
è
æ
t
t
-t=
÷
ø
ö
ç
è
æ
t
-=
ò
t
22
1
0
2
0
0
00
I
Idt
t
Iq ,
откуда начальное значение силы тока равно:
t
=
0
0
2q
I . (4)
Таким образом, с учетом выражений (3) и (4) сила тока со време-
нем изменялась по закону:
÷
ø
ö
ç
è
æ
t
-
t
=
t
q
i 1
2
0
. (5)

84
Количество выделившейся теплоты в спирали определяется из
закона Джоуля-Ленца [7.1]:
()
=
÷
ø
ö
ç
è
æ
t
-
÷
ø
ö
ç
è
æ
t
-t-
t
=
÷
ø
ö
ç
è
æ
t
-
÷
ø
ö
ç
è
æ
t
==
òòò
ttt
0
2
2
2
0
0
2
2
0
0
2
11
4
1
2
t
d
t
Rq
dt
t
R
q
RdtiQ
()
t
=
÷
ø
ö
ç
è
æ
t
-t-
t
=
t
3
4
1
3
1
4
2
0
0
3
2
2
0
Rq
t
Rq
.
Ответ:
t
=
3
4
2
0
Rq
Q .
Пример 13. Плотность тока при электролизе медного купоро-
са составляет 100 А/м
2
. Определить толщину слоя меди, выделив-
шейся за 10 часов.
Дано:
100
=
j А/м
2
,
10
=
t ч 36000
=
с,
96480
=
F Кл/моль.
Найти: h .
Решение. Согласно закону Фарадея для электролиза [8.4]
масса выделившегося на электроде вещества равна:
It
Z
M
F
m
1
= , (1)
где
F
– постоянная Фарадея,
M
– молярная масса вещества,
Z
–
валентность,
I
– сила постоянного тока, протекающего через
электролит,
t
– время протекания тока.
Сила тока связана с плотностью тока соотношением [5.2]:
jSI
=
, (2)
где S – площадь поперечного сечения проводника.
Учитывая выражение (2), закон Фарадея (1) примет вид:
jSt
Z
M
F
m
1
= . (3)

85
С другой стороны, масса выделившегося вещества может
быть получена из соотношения:
ShVm
r
=
r
=
, (4)
где
r
– плотность выделившегося вещества, h – толщина слоя
(считая ее одинаковой по всей поверхности) выделившегося ве-
щества.
Подставляя (4) в (3) и выражая искомую толщину слоя, получим:
r
=
FZ
Mjt
h
или с учетом числовых значений величин
4
10337,1
8930
2
96480
36000100064,0
-
×=
××
××
=h м.
Ответ:
4
10337,1
-
×=h м.
Пример 14. Между пластинами конденсатора площадью
370 см
2
находится водород объемом 320 см
3
. При подаче напряже-
ния 52,4 В на конденсатор сила проходящего через него тока со-
ставила
6
107,2
-
× А. Найти концентрацию ионов в газе, если под-
вижность положительных ионов 4,5=
+
b см
2
/(В×с), а отрицатель-
ных – 4,7=
-
b см
2
/(В×с).
Дано:
370
=
S см
22
107,3
-
×= м
2
,
320
=
V см
34
102,3
-
×= м
3
,
4,52
=
U В,
6
107,2
-
×=I А,
4,5=
+
b см
2
/(В×с)
4
104,5
-
×= м
2
/(В×с),
4,7=
-
b см
2
/(В×с)
4
104,7
-
×= м
2
/(В×с).
Найти:
n
.
Решение. Так как электрическое поле в плоском конденсато-
ре однородно, то напряженность поля связана с напряжением ме-
жду обкладками соотношением [3.10]:
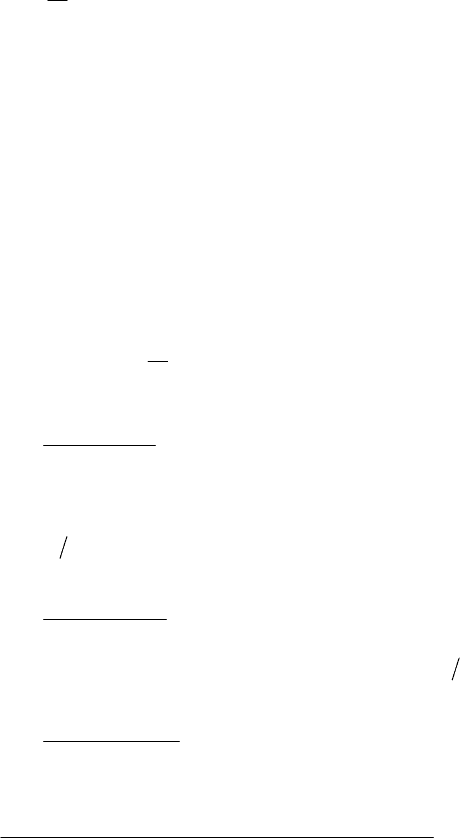
86
d
U
E = , (1)
где d – расстояние между обкладками конденсатора.
Если между обкладками конденсатора в однородном электро-
статическом поле имеются электрически заряженные частицы, то
под действием сил поля они начинают упорядоченно двигаться,
создавая таким образом электрический ток. Плотность тока в газе
при наличии ионов обоих знаков связана с напряженностью соот-
ношением (смотри [8.5], [8.6]):
(
)
Ebbqnj
-+
+= , (2)
где
+
b и
-
b – подвижности положительных и отрицательных ио-
нов, соответственно,
q
– заряд иона,
n
– концентрация ионов.
Из соотношений (1) и (2) получим выражение:
()
d
U
bbqnj
-+
+= . (3)
Искомая концентрация запишется в виде:
()
-+
+
=
bbqU
jd
n
. (4)
Объем газа, заключенного между обкладками конденсатора,
равен SdV
=
, где S – площадь пластин, откуда:
SVd = . (5)
Подставляя (5) в (4), получим:
()
-+
+
=
bbSqU
jV
n
. (6)
Учитывая определение плотности тока [5.2] SIj = , выражение
(6) приобретет окончательный вид:
()
-+
+
=
bbqUS
IV
n
2
.
Подставляя числовые значения величин, находим:
()()
13
4419
2
2
46
109,5
104,7104,54,52106,1107,3
102,3107,2
×=
×+××××××
×××
=
----
--
n м
-3
.
Ответ:
13
109,5 ×=n м
-3
.

87
Пример 15. Определить индукцию магнитного поля в центре
кругового проводника с током и на оси в точке, расположенной на
расстоянии 12 см от его плоскости. Радиус кольца 8,0 см, сила то-
ка 2,5 A.
Дано:
12
=
a см 12,0
=
м,
0,8
=
R см 080,0
=
м,
5,2
=
I А.
Найти:
0
B ,
B
.
Решение. Проводники с током создают вокруг себя магнит-
ное поле. Если такой проводник разбить на бесконечно малые
элементы, то каждый элемент тока ( lId
r
) создает в разных точках
пространства свое микрополе с магнитной индукцией бесконечно
малой величины, которая может быть определена согласно закону
Био-Савара-Лапласа [9.11]:
3
0
][
4
r
rldI
Bd
r
r
r
´
p
mm
= (1)
или для модуля вектора Bd
r
:
2
0
sin
4
r
Idl
dB
a
p
m
m
= , (2)
где
0
m – магнитная постоянная,
m
– магнитная проницаемость
среды, в которой создано магнитное поле (в условиях данной за-
дачи 0,1
=
m
),
a
– угол между ld
r
и rd
r
.
Выделим в проводнике с током два равных по величине эле-
мента тока
1
lId
r
и
2
lId
r
, размещенных на концах одного и того же
диаметра кольца (рис. 1.47).
Векторы индукции магнитного поля, созданные этими эле-
ментами тока, равны соответственно
1
Bd
r
и
2
Bd
r
в точке O
¢
, не
совпадают по направлению, но равны по абсолютной величине.
Тогда индукция магнитного поля, созданного элементами
1
ld
r
и
2
ld
r
с током, вдоль оси OO
¢
(рис. 1.47) составляет:

88
r
R
dBdBdB
11
2sin2 =b= . (3)
Так как индукция магнитного поля, созданного элементом то-
ка на расстоянии
r
от него, равна
2
10
1
4 r
Idl
dB
p
m
= , (4)
где учтено, что 2p=a , а расстояние
r
может быть найдено по
теореме Пифагора:
(
)
21
2222
aRaRr +=+= , (5)
то выражение (3) с учетом (4) и (5) приобретет вид:
()
2/3
22
0
2aR
IRdl
dB
+p
m
= . (6)
Так как магнитное поле создается всем круговым током, то
результирующая индукция магнитного поля в точке O
¢
может
быть получена путем сложения бесконечно малых величин индук-
ции, созданных всеми элементами тока, то есть интегрирования
выражения (6):
() ()
2/3
22
2
0
0
2/3
22
0
22 aR
IR
dl
aR
IR
dBB
R
+
m
=
+p
m
==
òò
p
. (7)
Рис. 1.47

89
Интегрирование производится по длине кругового тока от 0
до половины длины окружности R
p
, так как в (3) учтены индук-
ции полей, созданных двумя элементами тока.
Если в равенстве (7) положить 0
=
a , то получим выражение
для нахождения индукции магнитного поля в центре кольца с то-
ком:
R
I
B
2
0
0
m
= . (8)
Подставляя числовые значения величин в (7) и (8), получим:
()
6
2/3
22
27
103,3
12,0080,02
080,05,21014,34
-
-
×=
+
××××
=B Тл,
6
7
0
100,20
080,02
5,21014,34
-
-
×=
×
×××
=B Тл.
Ответ: 20
0
=B мкТл, 3,3
=
B мкТл.
Пример 16. Пройдя ускоряющую разность потенциалов
660 кВ, электрон влетает в однородное магнитное поле перпенди-
кулярно линиям магнитной индукции. Частица двигается по ок-
ружности радиусом 5,0 см. Определить индукцию магнитно-
го поля.
Дано:
660
=
U кВ
5
106,6 ×= В,
0,5
=
r см 050,0
=
м.
Найти:
B
.
Решение. Задачу целесообразно решать в два этапа, так как
первоначально электрон движется под действием сил электриче-
ского поля, а после разгона до некоторой скорости движется в
магнитном поле. Сначала необходимо выяснить: классической или
релятивистской частицей является электрон в условиях данной
задачи.
Работа сил электрического поля [3.7] идет на изменение кине-
тической энергии электрона (полагаем, что имеем дело с класси-
ческой частицей):

90
2
2
u
=
m
eU , (1)
откуда скорость электрона с учетом данных задачи равна
8
31
519
108,4
101,9
106,6106,122
×=
×
××××
==u
-
-
m
eU
м/с.
Убеждаемся, что полученная скорость превышает скорость света в
вакууме, а, значит, электрон в данной задаче необходимо рассмат-
ривать как частицу релятивистскую. То есть, кинетическая энер-
гия релятивистской частицы равна разности полной энергии и
энергии покоя:
2
0
2
cmmcT -= , (2)
где
0
m – масса покоя электрона,
c
– скорость света в вакууме.
С приближением скорости электрона к скорости света его
масса возрастает и определяется из соотношения:
2
0
1 b-
=
m
m , (3)
где cu=b .
Теорема об изменении кинетической энергии (1) с учетом со-
отношений (2) и (3) запишется в виде:
÷
÷
ø
ö
ç
ç
è
æ
-
b-
= 1
1
1
2
2
0
cmeU . (4)
В результате преобразований получим:
2
2
0
2
1
1
1
÷
÷
ø
ö
ç
ç
è
æ
+=
b- cm
eU
,
2
2
0
1
1
1
÷
÷
ø
ö
ç
ç
è
æ
+
-=b
cm
eU
, (5)
подставляя числовые значения в выражение (5), вычислим сначала
b
, а затем скорость электрона, с которой он влетает в магнит-
ное поле:
