Аскирка В.Ф. Электричество и магнетизм. Волновая оптика
Подождите немного. Документ загружается.


71
2
0
4
1
r
q
E
r
pe
=
,
где
r
E – проекция вектора напряженности
E
r
на направление ра-
диус-вектора
r
r
, совпадающего по направлению с нормалью к по-
верхности сферы в каждой ее точке. Знак заряда здесь определяет
знак проекции
r
E , а, следовательно, и направление самого векто-
ра
E
r
: от заряженной сферы (при 0
>
q ) или к ней (при 0
<
q ).
Если
R
r
<
, то замкнутая поверхность (рис. 1.43) не содержит
внутри зарядов, следовательно, отсутствует поток вектора напря-
женности, поэтому в этой области всюду 0
=
E , то есть внутри
равномерно заряженной сферической поверхности напряженность
электростатического поля отсутствует.
Вне сферической поверхности поле убывает с расстоянием от
ее центра по такому же закону, как у точечного заряда (обратно
пропорционально
2
r
) [1.7].
График зависимости напряженности электростатического по-
ля заряженной сферы от расстояния отображен на рисунке 1.6 в
главе «Теорема Гаусса для электростатического поля в вакууме».
Ответ:
2
0
4
1
r
q
E
r
pe
=
, (
R
r
>
); 0
=
E , (
R
r
<
).
Пример 6. Два положительных точечных заряда 2,0 мкКл и
15 нКл находятся в вакууме на расстоянии 2,0 м друг от друга. За-
ряды сближают до расстояния 1,5 м. Какая работа совершается
при их сближении?
Дано:
0,2
1
=q мкКл
6
100,2
-
×= Кл,
15
2
=q нКл
8
105,1
-
×= Кл,
0,2
1
=r м,
5,1
2
=r м.
Найти:
A
¢
.

72
Решение. В условиях данной задачи можно предложить два
способа решения.
Первый способ. Согласно определению [3.1] работа некоторой
силы может быть найдена из соотношения:
rdFdA
r
r
×= . (1)
Так как сила, действующая на заряды, – переменная, то для нахо-
ждения работы по сближению точечных зарядов необходимо вы-
ражение (1) проинтегрировать:
ò
×= rdFA
r
r
. (2)
Сила электростатического взаимодействия двух точечных зарядов
определяется из закона Кулона [1.2], поэтому интеграл (2) запи-
шем в виде:
ò
pe
= dr
r
qq
A
2
21
0
4
1
. (3)
Учитывая, что работа внешней силы
A
¢
по перемещению заряда
равна по модулю и противоположна по знаку работе сил поля
A
,
получим:
ò
pe
-=
¢
2
1
2
21
0
4
1
r
r
dr
r
qq
A . (4)
После интегрирования искомая работа запишется в виде:
÷
÷
ø
ö
ç
ç
è
æ
-
pe
=
pe
=
pe
-=
¢
ò
120
21
0
21
2
0
21
11
4
1
44
2
1
2
1
rr
qq
r
qq
r
dr
qq
A
r
r
r
r
. (5)
После подстановки числовых значений получим окончательный
ответ:
5
12
86
105,4
0,2
1
5,1
1
1085,814,34
105,1100,2
-
-
--
×=
÷
÷
ø
ö
ç
ç
è
æ
-
×××
×××
=
¢
A
Дж.
Второй способ. Работа
A
¢
, совершаемая внешней силой по
перемещению заряда в электрическом поле из одной точки в дру-
гую, равна по абсолютному значению и противоположна по знаку
работе
A
сил поля по перемещению заряда между теми же точка-
ми:
.AA -=
¢
(6)

73
Работа сил электростатического поля по перемещению заряда
между двумя точками может быть определена через разность
потенциалов между теми же точками [3.7]:
(
)
21
j-j= qA ,
или с учетом соотношения (6) примет вид:
(
)
(
)
1221
j-j=j-j-=
¢
qqA . (7)
В данной задаче заряд
1
q оставим неподвижным, а заряд
2
q
под действием внешних сил будет перемещаться в поле, создан-
ном зарядом
1
q , из точки, находящейся на расстоянии
1
r , в точку,
находящуюся на расстоянии
2
r от заряда.
Так как заряд
1
q по условию задачи является точечным, то
потенциалы поля в соответствующих точках определяются из вы-
ражений [3.5]:
1
1
0
1
4
1
r
q
pe
=j
, (8)
2
1
0
2
4
1
r
q
pe
=j
. (9)
Подставляя выражения для потенциалов (8) и (9) в (7), не забывая,
что переносимый заряд –
2
q , получим:
÷
÷
ø
ö
ç
ç
è
æ
-
pe
=
÷
÷
ø
ö
ç
ç
è
æ
pe
-
pe
=
¢
120
21
1
1
02
1
0
2
11
44
1
4
1
rr
qq
r
q
r
q
qA . (10)
Выражение (10) совпадает с ответом (5), полученным первым спо-
собом.
Ответ:
5
105,4
-
×=
¢
A Дж.
Пример 7. Определить энергии каждого из трех конденсато-
ров с емкостями, равными 1,0 нФ, 2,0 нФ, 3,0 нФ при последова-
тельном и параллельном подключении их в цепь с напряжением
600 В.
Дано:
0,1
1
=C нФ
9
100,1
-
×= Ф,

74
0,2
2
=C нФ
9
100,2
-
×= Ф,
0,3
3
=C нФ
9
100,3
-
×= Ф,
600
=
U В.
Найти:
1
W ,
2
W ,
3
W ,
1
W
¢
,
2
W
¢
,
3
W
¢
.
Решение. Энергия конденсатора емкостью C , заряженного
до напряжения U , определяется соотношениями [4.18], [4.19]:
C
qCU
W
2
2
22
== . (1)
В случае параллельного соединения конденсаторов напряже-
ние на каждом из них одинаково и равно 600 В. Подставив в вы-
ражение (1) заданные значения величин, получим для энергии ка-
ждого конденсатора:
4
29
2
1
1
108,1
2
600100,1
2
-
-
×=
××
==
UC
W Дж,
4
2
106,3
-
×=W Дж,
4
3
104,5
-
×=W Дж.
В случае последовательного соединения конденсаторов заряд
q
на каждом из них одинаков и равен общему заряду батареи
конденсаторов. Эквивалентная емкость трех последовательно со-
единенных конденсаторов находится из соотношения [4.14]:
321
1111
CCCC
++=
, (2)
откуда искомая емкость
313221
321
CCCCCC
CCC
C
++
=
. (3)
Заряд такой системы равен:
313221
321
CCCCCC
UCCC
CUq
++
==
. (4)
Подставляя (4) в (1), получим выражение для энергии одного кон-
денсатора в случае его последовательного соединения в батарее:
(
)
()
2
313221
2
321
1
2CCCCCC
UCCC
W
++
=
¢
, (5)
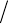
75
аналогичные выражения можно получить для двух других конден-
саторов. Подставляя числовые значения величин в расчетные фор-
мулы (5) и ей аналогичные для двух других конденсаторов,
получим:
5
1
104,5
-
×=
¢
W Дж,
5
2
107,2
-
×=
¢
W Дж,
5
3
108,1
-
×=
¢
W Дж.
Ответ:
4
1
108,1
-
×=W Дж,
4
2
106,3
-
×=W Дж,
4
3
104,5
-
×=W Дж,
5
1
104,5
-
×=
¢
W Дж,
5
2
107,2
-
×=
¢
W Дж,
5
3
108,1
-
×=
¢
W Дж.
Пример 8. К источнику тока с ЭДС 100 В и внутренним со-
противлением 20 Ом подключен потенциометр с сопротивлением
40 Ом (рис. 1.44 а). Определить показания вольтметра сопротив-
лением 400 Ом, подключенного к одной из клемм потенциометра
и подвижному контакту, установленному посередине потенцио-
метра. Какова разность потенциалов между теми же точками по-
тенциометра при отключении вольтметра?
Дано:
40
=
R Ом,
100
=
E
В,
20
=
r Ом,
400=
V
R Ом.
Найти:
V
U , U .
Решение. Перерисуем схему иначе, «разбив» потенциометр
скользящим контактом на два резистора (рис. 1.44 б). Вольтметр и
половина сопротивления потенциометра 2R соединены парал-
лельно и составляют общее сопротивление
1
R . Вольтметр при та-
ком подключении показывает напряжение на сопротивлении
1
R :
11
RIU
V
= , (1)
где
1
I – сила тока в неразветвленной части цепи.
Сила тока
1
I определяется по закону Ома для замкнутой цепи
[5.19]:

76
rR
I
+
=
2
1
E
, (2)
где
2
R – сопротивление внешней цепи.
Сопротивление внешней цепи состоит из двух последователь-
но соединенных сопротивлений
1
R и 2R , то есть равно сумме
двух сопротивлений [5.13]:
2
12
RRR += . (3)
Сопротивление R
1
определяется с использованием соотношения
[5.14]:
,
2
111
1
RRR
V
+=
откуда
V
V
RR
RR
R
2
1
+
=
. (4)
Сопротивление
2
R из выражения (3) с учетом (4) может быть вы-
ражено в виде:
()
(
)
()
V
V
V
VV
V
V
RR
RRR
RR
RRRRR
R
RR
RR
R
22
4
22
22
22
2
2
+
+
=
+
++
=+
+
=
. (5)
Вычисляя, находим:
(
)
()
39
4002402
40044040
2
=
×+
×+
=R Ом. (6)
Рассчитаем силу тока в неразветвленной части цепи, используя (2)
с учетом полученного значения величины (6):
69,1
20
39
100
1
=
+
=I А. (7)
Рис. 1.44
77
Подставляя в (4) числовые значения, найдем величину сопротив-
ления
1
R :
05,19
400
2
40
40040
1
=
×+
×
=R Ом.
Подставляя рассчитанные значения силы тока и сопротивления в
выражение (1), найдем показания вольтметра:
2,3205,1969,1 =×=
V
U В.
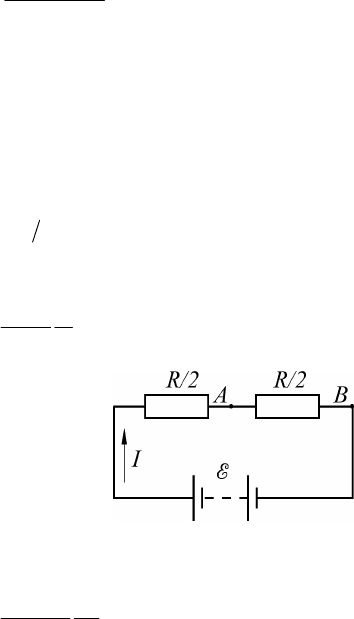
Разность потенциалов между точками
A
и
B
при отключенном
вольтметре (рис. 1.45) равна произведению силы тока
I
, который
течет через потенциометр, на половину сопротивления потенцио-
метра:
(
)
2RIU = ,
или с учетом закона Ома для замкнутой цепи (при отключенном
вольтметре):
2
R
r
R
U
+
=
E
.
Подставляя числовые значения величин, получим:
3,33
2
40
20
40
100
=
+
=U В.
Ответ: 2,32=
V
U В, 3,33
=
U В.
Пример 9. На медный проводник длиной 1,0 м и площадью
поперечного сечения 10 мм
2
подано напряжение, изменяющееся
по закону
(
)
tu 314sin310= В. Определить заряд, который протекает
по проводнику за первые 5,0 мс.
Рис. 1.45

78
Дано:
10
=
S мм
25
100,1
-
×= м
2
,
(
)
tu 314sin310= В,
0,5
=
D
t мс
3
100,5
-
×= с,
17
=
r
нОм×м
8
107,1
-
×= Ом×м.
Найти:
q
.
Решение. Так как напряжение на концах проводника изменя-
ется, то и сила тока в нем также будет изменяться. Для нахожде-
ния заряда, прошедшего через поперечное сечение проводника,
воспользуемся определением [5.1], разбивая весь рассматривае-
мый интервал времени на бесконечно большое число бесконечно
малых интервалов времени dt :
idtdq
=
, (1)
где
i
– значение силы тока к моменту начала интервала вре-
мени dt .
Для нахождения заряда, прошедшего в течение конечного
промежутка времени, необходимо выражение (1) проинтегриро-
вать, следовательно:
ò
D
=
t
dtiq
0
. (2)
Силу тока по закону Ома для однородного участка цепи [5.15]
выразим через напряжение, тогда интеграл (2) запишется в виде:
ò
D
=
t
dt
R
u
q
0
, (3)
где
u
– изменяющееся напряжение, приложенное к концам про-
водника,
R
– сопротивление проводника.
Сопротивление проводника связано с его длиной l и площа-
дью поперечного сечения S соотношением [5.9]:
S
l
R r= , (4)
где
r
– удельное сопротивление проводника (числовое значение
необходимо брать из приложения 12).
С учетом (4) выражение (3) примет вид:

79
ò
D
r
=
t
dt
l
uS
q
0
. (5)
Подставляя заданное выражение для изменяющегося напряжения
и производя интегрирование, получим:
() ()()
t
l
S
dtt
l
S
q
t
D-
r
=
r
=
ò
D
314cos1
314
310
314sin
310
0
.
Подставляя числовые значения величин, получим:
()()
580100,5314cos1
0,1107,1314
100,1310
3
8
5
=××-
×××
××
=
-
-
-
q
Кл.
Ответ: 580
=
q Кл.
Пример 10. Определить силу тока, протекающего через со-
противление
R
в схеме (рис. 1.46). Сопротивления
R
,
1
R ,
2
R , а
также ЭДС
1
E ,
2
E заданы. Внутренними сопротивлениями источ-
ников пренебречь.
Дано:
R
,
1
R ,
2
R ,
1
E ,
2
E .
Найти:
I
.
Решение. Изображенная схема (рис. 1.46) представляет собой
разветвленную цепь, для расчета которой целесообразно восполь-
зоваться правилами Кирхгофа. На схеме имеются два узла (
A
и
B
), а также три ветви (
ARB
, BAR
1
и BAR
2
). Следовательно, в
каждой из этих ветвей текут неизвестные токи
I
,
1
I и
2
I . Обозна-
чим на рисунке стрелками их предположительные направления (на
свое усмотрение).
Согласно первому правилу Кирхгофа [6.1] алгебраическая
сумма токов, сходящихся в узле, равна нулю:
0
21
=++ III . (1)

80
Пользуясь вторым правилом Кирхгофа [6.2], запишем еще два
уравнения для двух произвольно выбранных контуров (в общем
случае контуров должно быть столько, пока все элементы не будут
входить в уравнения). Возьмем контуры AARBR
1
и AARBR
2
,
содержащие сопротивления соответственно
R
,
1
R и
R
,
2
R
(рис. 1.46). Выбрав направление обхода каждого контура по часо-
вой стрелке, запишем (используя правило знаков):
111
E-=+- RIIR , (2)
222
E=+- RIIR . (3)
Полезно убедиться, что соответствующее уравнение для кон-
тура, содержащего
1
R и
2
R , является следствием (2) и (3). Решив
систему трех уравнений (1) – (3), получим выражение для нахож-
дения величины искомого тока:
2121
1221
RRRRRR
RR
I
++
+
-
=
EE
.
Если после подстановки числовых значений окажется, что
0
>
I , то это значит, что в действительности ток течет так, как мы
предположили на рис. 1.46, если же 0
<
I , то – в противополож-
ном направлении.
Ответ:
2121
1221
RRRRRR
RR
I
++
+
-
=
EE
.
Рис. 1.46
