Аскирка В.Ф. Электричество и магнетизм. Волновая оптика

Подождите немного. Документ загружается.

181

Уравнение стоячих волн, возникающих вдоль оси OX , име-

ет вид:

ss w

= cos

cos2

. (14.12)

Множитель

cos

показывает, что колебания точек среды с

различными координатами осуществляются синфазно, то есть в

одинаковой фазе ( 0cos

t ) либо в противофазе ( 0cos

t ) с

колебаниями источника волны. Множитель

(

)

lpxs 2cos2

пред-

ставляет собой амплитуду стоячей волны, которая изменяется по

гармоническому закону вдоль направления OX , однако имеет по-

стоянное значение для данной точки.

В стоячей волне нет направленного переноса энергии. При

стационарном распределении энергии вдоль направления OX рас-

сматривают характерные точки – узлы стоячей волны (встреч-

ные бегущие волны приходят в противофазе, гасят друг друга, по-

этому частицы среды в этом месте колебаний не совершают) и

пучности (встречные бегущие волны приходят в одинаковых фа-

зах и усиливают друг друга, поэтому частицы среды в этом месте

колеблются с максимальной амплитудой

2s ).

Расстояние между двумя соседними узлами или пучностями

(равно половине длины бегущей волны 2l ) называется длиной

стоячей волны.

В струне, стержне или воздушной трубе длиной l на концах

происходят многократные отражения волн. В этом случае стоячая

волна стационарной формы может существовать лишь при опре-

деленных условиях.

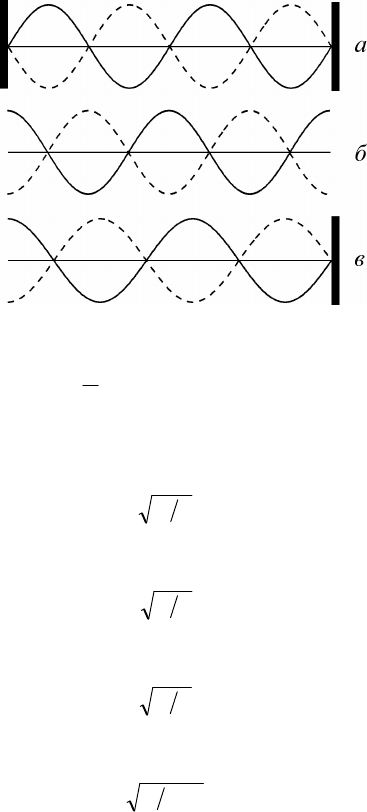
Если оба конца струны или стержня закреплены или не закре-

плены (в воздушной трубе – закрыты или открыты торцы с обеих

сторон) (рис. 2.3 а и б), то могут образовываться только такие

стоячие волны, для которых на длине l укладывается целое число

полуволн длины бегущей волны. В первом случае на концах (тор-

цах) будут наблюдаться узлы, а во втором – пучности:

lm =

, ( ,1

m ,2 …). (14.13)

Если один из концов струны или стержня закреплен (для воз-

душной трубы – закрыт один из торцов) (рис. 2.3 в), то стоячие

182

волны образуются, если на длине l укладывается нечетное число

четвертей длин волн бегущей волны. При этом на закрепленном

конце (закрытом торце) будет находиться узел, а на свободном –

пучность:

()

lm=

12, ( ,0

m ,1,2 …). (14.14)

Скорости распространения монохроматических волн в

различных средах можно рассчитать из следующих выражений:

продольных волн в неограниченной упругой среде:

r=u K , (14.15)

где

– модуль всестороннего сжатия,

– плотность среды;

продольных волн в тонких стержнях:

r=u E , (14.16)

где

– модуль упругости (модуль Юнга),

– плотность стержня;

поперечных (сдвиговых) волн в неограниченной упругой среде:

r=u G , (14.17)

где G – модуль сдвига,

– плотность среды;

поперечных волн в натянутой нити (струне):

(

)

r=u SF , (14.18)

Рис. 2.3

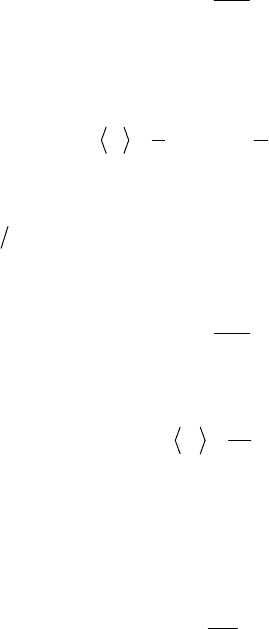
183

где

– сила, растягивающая нить; S – площадь поперечного се-

чения нити,

– плотность среды.

Последнее выражение (14.18) справедливо лишь в случае, ко-

гда напряжение, вызванное сдвигом, мало по отношению к напря-

жению, вызванному растягивающей силой.

Для характеристики энергии волны используется понятие

объемной плотности энергии, которая равна отношению энергии

волны dW в некотором объеме к величине этого объема dV :

w = . (14.19)

Среднее значение объемной плотности энергии волны, имеющей

амплитуду

s и циклическую частоту

и распространяющейся в

упругой среде, равно

()

wr=

sdttww , (14.20)

где

– промежуток времени, в течение которого производится

усреднение (выбирается много большим периода колебаний волны

wp>>t 2 ).

Поток энергии волны равен мощности, переносимой волной

через некоторую площадку:

=F . (14.21)

Соответственно, среднее по времени значение потока энергии

волны будет равно:

=F . (14.22)

Вектором плотности потока энергии J

(вектором Умова)

называется вектор, модуль которого равен отношению потока, пе-

реносимого некоторой волной через площадку, ориентированную

перпендикулярно направлению ее распространения, к площади

этой площадки:

= , (14.23)

где j

– единичный вектор, ориентированный вдоль направления

распространения волны.

184

Вектор Умова может быть также выражен через фазовую скорость

и объемную плотность энергии волны:

jwJ

u= . (14.24)

Среднее по времени значение модуля вектора Умова J на-

зывают интенсивностью волны

()

dttJJI , (14.25)

где

– некоторый промежуток времени, значительно больший

периода колебаний ( wp>>t 2 ).

Для монохроматической волны, распространяющейся в

упругой среде, интенсивность равна

uwr=

sI , (14.26)

где

– плотность среды, в которой распространяется волна.

При распространении волн в поглощающей среде их интен-

сивность уменьшается в соответствии с законом Бугера:

eII

= , (14.27)

где

– показатель поглощения,

I – начальная интенсивность

плоских волн,

– интенсивность волн после прохождения рас-

стояния

в среде.

15. ЗВУКОВЫЕ ЯВЛЕНИЯ

Механические колебания в интервале частот 16 – 20000 Гц

называются звуковыми. Соответствующие им упругие волны в

среде (как правило, в воздухе) называются звуком. Волны с часто-

той меньшей 16 Гц называются инфразвуком, а с частотой боль-

шей 20000 Гц – ультразвуком.

Характеристиками звука являются высота, тембр и сила звука.

Высота звука определяется частотой звуковых колебаний. Тембр

звука определяется соотношением амплитуд обертонов (то есть

колебаний, частота которых кратна частоте основного тона) и ам-

плитуды основного тона.

Сила звука – это интенсивность звуковой волны (среднее

значение модуля вектора Умова).

185

Наименьшее значение силы звуковых волн

I , воспринимае-

мых ухом человека, называется порогом слышимости. Величине

I соответствует некоторое значение минимального звукового

давления

pD , вызывающего звуковые ощущения. Порог слыши-

мости зависит от частоты звука. Наибольшая чувствительность

человеческого уха наблюдается для волн с частотой 1000 –

4000 Гц. В частности, для частоты 3000 Гц порог слышимости со-

ставляет

100,1

×=I Вт/м

. Это значение принято считать поро-

гом слышимости. Соответствующее ему минимальное звуковое

давление равно

100,1

×=Dp Па.

Для сравнения силы звуковых волн пользуются величиной,

называемой уровнем громкости, равной десятичному логарифму

отношения интенсивности

данной звуковой волны к

величине

I :

L =

(15.1)

или

, (15.2)

где p

– звуковое давление в данном волновом процессе.

Единица измерения громкости, определяемой из (15.1), называ-

ется белом (Б). Один бел громкости имеет волна, интенсивность ко-

торой превосходит в 10 раз пороговое значение. На практике поль-

зуются единицей измерения в 10 раз меньшей бела – децибелом

(дБ). Уровень громкости в децибелах определяется выражением:

lg10lg10

. (15.3)

В газах возможно распространение только продольных звуко-

вых волн, скорость которых определяется выражением:

rg=u p , (15.4)

где

– соответственно давление и плотность газа, невозму-

щенного волной,

– отношение теплоемкостей газа при постоян-

ном давлении и постоянном объеме:

cc=g .

186

Выражение для скорости распространения продольных звуко-

вых волн в идеальном газе имеет вид:

RTg

=u , (15.5)

где

– универсальная газовая постоянная;

– молярная масса

газа,

– термодинамическая температура.

Связь между интенсивностью звуковой волны и амплитудой

давления

(

)

max

pD (разностью между давлением в волновом поле и

давлением в той же среде при отсутствии волнового процесса):

(

)

max

I . (15.6)

Эффект Доплера состоит в том, что воспринимаемая частота

звука зависит от относительного движения источника волн и на-

блюдателя (приемника), воспринимающего эти волны.

В случае движения источника звука частоты

n со скоростью u

воспринимаемая наблюдателем частота будет равна

n=n

. (15.7)

В случае движения наблюдателя со скоростью u

воспринимаемая

наблюдателем частота будет равна

±n=n 1

. (15.8)

В обоих выражениях (15.7 и 15.8)

– скорость звука; знак «+»

соответствует приближению источника к наблюдателю, «–» соот-

ветствует их удалению.

16. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Взаимосвязанные колебания электрических и магнитных по-

лей, распространяющиеся в пространстве с конечной скоростью,

называются электромагнитной волной.

Электромагнитные волны в вакууме и изотропной среде пред-

ставляют собой колеблющиеся во взаимно перпендикулярных

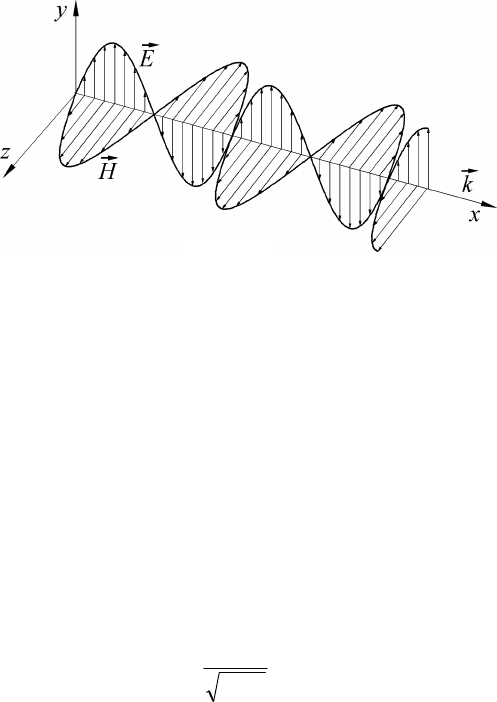
187

плоскостях векторы напряженности электрического

и магнит-

ного

полей, которые вместе с волновым вектором k

образуют

правую тройку векторов (рис. 2.4). Это означает, что электромаг-

нитные волны являются поперечными.

Как и волны в упругой среде, электромагнитные волны быва-

ют плоские и сферические. Уравнение плоской бегущей моно-

хроматической волны для напряженности электрического поля

электромагнитной волны

может быть записано в виде:

(

)

rkrEE

×-w= cos

, (16.1)

где

– радиус-вектор, проведенный в некоторую точку, в которой

определяется

, k

– волновой вектор.

Направление волнового вектора перпендикулярно волновой

поверхности (волновому фронту), его модуль равен волновому

числу. Аналогично (16.1) может быть записано уравнение для на-

пряженности магнитного поля

Скорость распространения электромагнитных волн в ва-

кууме определяется из соотношения:

=с , (16.2)

где

e – электрическая постоянная,

m – магнитная постоянная.

Скорость распространения электромагнитных волн в сре-

де с диэлектрической проницаемостью

и магнитной проницае-

мостью

равна

Рис. 2.4

188

. (16.3)

Абсолютным показателем преломления среды называется

величина, равная отношению

n . (16.4)

Принимая во внимание (16.3) и (16.4), можно получить соотноше-

ние, связывающее коэффициент преломления с диэлектрическими

и магнитными свойствами среды:

em=n . (16.5)

Связь между напряженностью электрического поля и индук-

цией магнитного поля в электромагнитной волне задается выра-

жением:

cBnE

. (16.6)

При распространении электромагнитной волны из вакуума в

среду с показателем преломления

ее частота не изменяется

w=w , а длина волны уменьшается в

раз: n/

l=l (

w ,

круговая частота и длина волны соответственно в вакууме

и среде).

Вектор Умова-Пойнтинга в электромагнитной волне опреде-

ляется из векторного произведения:

][ HES

´= , (16.7)

где

– напряженность электрического поля,

– напряженность

магнитного поля.

Модуль вектора Умова-Пойнтинга имеет смысл плотности

потока электромагнитной энергии и равен мощности, переноси-

мой электромагнитной волной через некоторую единичную пло-

щадку, ориентированную перпендикулярно направлению ее рас-

пространения.

В оптически изотропной среде направление вектора Умова-

Пойнтинга совпадает с направлением волнового вектора (рис. 2.4).

Оптически изотропными называют среды, оптические свой-

ства которых одинаковы по всем направлениям.

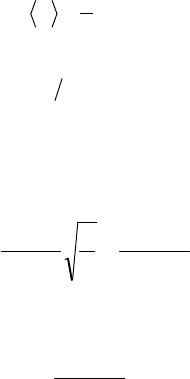
189

Среднее по времени значение модуля вектора Умова-

Пойнтинга называют интенсивностью электромагнитной волны:

)(

dttSSI , (16.8)

где

– некоторый промежуток времени, значительно больший

периода колебаний: wp>>t 2 .

Для изотропной среды, характеризуемой диэлектрической и

магнитной проницаемостями, соответственно

, интенсив-

ность бегущей монохроматической электромагнитной волны оп-

ределяется выражением:

cnEcE

. (16.9)

Для большинства оптически прозрачных диэлектриков 1

, по-

этому выражение (16.9) для подобных сред запишется в виде:

cnE

= . (16.10)

17. ФОТОМЕТРИЯ

Фотометрия – совокупность методов измерения энергетиче-

ских и световых характеристик электромагнитного излучения оп-

тического (видимого) диапазона.

Для измерения энергии в фотометрии используются два мето-

да: объективный и визуальный (субъективный). В случае ис-

пользования объективного метода величина энергии измеряется на

основании воздействия электромагнитной волны на фотоприем-

ник, причем сигнал, вырабатываемый фотоприемником, является

зависимым от энергии или интенсивности электромагнитной вол-

ны. При использовании визуального метода величины, характери-

зующие энергию волны, оцениваются по зрительному восприятию

глаза человека. В зависимости от метода измерения используются

два типа фотометрических величин: энергетические и световые.

190

Энергетические фотометрические величины

Основной энергетической величиной в фотометрии является

энергетический поток излучения (поток излучения)

F , харак-

теризующий среднюю мощность излучения, которая переносится

электромагнитной волной через некоторую поверхность площа-

дью S :

sñá==F dSР

, (17.1)

где P – среднее значение мощности излучения.

Энергетическая освещенность

E – отношение потока излу-

чения, который падает на площадку, к величине ее площади

. (17.2)

Если падающий поток распределен на площадке неравномерно, то

равенство (17.2) определяет среднюю освещенность.

Под освещенностью в окрестности некоторой точки следу-

ет понимать величину, равную

E , (17.3)

где

d – некоторая элементарная площадка, в пределах которой

световой поток можно считать постоянным.

Величина, равная произведению освещенности на промежу-

ток времени, в течение которого эта освещенность создается на

данной площадке, называется энергетической экспозицией:

EH = . (17.4)

Энергетическая экспозиция характеризует интегральный эффект,

производимый электромагнитной волной на фотоприемник.

Для характеристики точечных источников излучения исполь-

зуют величину, которую называют энергетической силой излу-

чения

J , равную отношению величины потока излучения, излу-

чаемого внутрь телесного угла

d , к величине этого угла

(рис. 2.5):

. (17.5)