Багиев Г.Л. Тарасевич В.М. Анн Х. Маркетинг

Подождите немного. Документ загружается.

Если

средняя рыночная цена аналогичных товаров

330

тыс.руб.,

то

цена каж-

дого товара равна произведению средней

рыночной

оценки

одного балла на число

баллов, присвоенных изделию. Средняя рыночная оценка одного балла равна

тыс.

руб. (330/33). Цена товара

составляет 420 тысруб., товара В —

330

тыс.,

товара

—

250

тыс.

руб.

Метод

структурной аналогии.

Суть этого метода сводится

следующему.

По

однотипной продукции

на

основе статистического материала определяется

структура

ее

себестоимости,

именно находится удельный

вес

материальных

затрат

заработной платы

полной себестоимости. Затем каким-либо методом

(например,

на

основе прямого исчисления

или

методом удельных показателей)

определяются абсолютные величины материальных затрат или заработной платы

по

новому изделию.

Зная

абсолютную величину того

или

иного вида затрат

по

новому изделию

и его

удельный

вес в

структуре

себестоимости,

по

анало-

гичной

группе продукции можно рассчитать ориентировочные затраты нового

изделия:

где

— себестоимость нового изделия;

(С

) — материальные затраты (заработная плата) на единицу нового изделия;

(А

)

— удельный вес материальных затрат (заработной платы)

себесто-

имости по аналогичной группе изделий.

Пример

Требуется определить

на

стадии технического задания проекта

нового топливного фильтра грубой очистки применительно

условиям освоен-

ного серийного производства

его

себестоимость (С

)

цену

(Цн),

если известно,

что

значение

основного параметра нового фильтра (П

) — пропускной способнос-

ти фильтра — равно

кг/ч, средние удельные затраты по основным материалам

(Уо.м). исчисленные

по

группе фильтров, равны

0,03

руб./кг/ч, удельный

вес за-

трат

по

основным материалам

(А

) в

полной себестоимости —

27,7

%, среднеот-

раслевая рентабельность

(Р)

— 18% полной себестоимости.

Затраты основных материалов (С

)

на

новый фильтр составляют:

.м

П„

0,03

0,75

руб.

Полная

себестоимость нового фильтра равна:

Ц„

(i+P)

2,70 х 1,18

3,18

руб.

Исчисленные

себестоимость

цена должны быть подвергнуты дополнитель-

ному анализу

осмыслению.

Агрегатный

метод. Он

заключается

суммировании себестоимости или цен

отдельных конструктивных частей или узлов изделия

учетом

стоимости ориги-

нальных узлов (деталей). Этот метод применяется, когда новая продукция состоит

341

из

разных основных конструктивных элементов (узлов, комплектующих изде-

лий),

цены или себестоимость которых

известны,

а совокупная цена или себесто-

имость продукции исчисляется как

сумма

себестоимости (цен) отдельных кон-

структивных элементов либо определяется

путем

суммирования (вычитания)

цен

либо себестоимости добавляемых или сменяемых элементов (узлов, комплек-

тующих

изделий).

Пример.

Проектная себестоимость новой топливной форсунки (Сф) на ста-

дии технического задания может быть определена суммированием себестоимости

узла

форсунки-распылителя (С

) и себестоимости форсунки без распылителя

(Сф

нр

т.е. Сф = С

Сф

нр

Себестоимость распылителя определяется методом

удельных

показателей — исходя из сложившихся затрат на единицу пропускной

способности распылителя аналогичных

форсунок.

Себестоимость непосредствен-

но

форсунки

(Сфнр)

определяется также методом

удельных

показателей — по ве-

личине

затрат на единицу массы форсунки.

Например,

если пропускная способность распылителя новой форсунки

равна 70 ммуцикл, масса форсунки без распылителя равна 0,22 кг, удельная

среднегрупповая величина затрат на единицу пропускной способности состав-

ляет 0,031 руб./мм

/цикл, удельная средняя величина затрат на единицу массы

форсунки

без распылителя — 6,2

руб./кг,

то себестоимость новой форсунки

будет

составлять: С

= 0,031 х 70 + 6,2 х 0,22 = 3,53 руб. Если принять отраслевой

норматив рентабельности к себестоимости равным

18%,

то ориентировочная цена

новой

форсунки

будет

равна: Ц

= С

х (1+0,18) « 3,35 х 1,18

«•

4,2 руб.

5.3.6.

Метод

статистических

игр

Известно,

что спрос на товары формируется под воздействием различных

факторов,

в том числе моды, вкусов, предпочтений покупателей, природно-кли-

матических факторов. Эти факторы обусловливают сезонный спрос на товары,

так

как на спрос сильное влияние оказывает изменение указанных факторов.

Влияние перечисленных выше факторов на изменение спроса особенно сказыва-

ется на

товарах

легкой промышленности (обувь,

одежда,

текстиль, галантерея и

т.д.). Не проданные вовремя товары

могут

и в

будущем

не найти своих покупате-

лей,

что приведет к потерям,

росту

торговых

издержек. В связи с этим торговые

предприятия

в конце сезона организуют расширенную распродажу сезонных то-

варов по сниженным ценам.

Понятно,

что решение о размере снижения цен при

сезонной

распродаже не может приниматься необдуманно. Прежде всего должна

учитываться предполагаемая реакция покупателей на снижение цен сезонных то-

варов, которая, как

известно,

измеряется эластичностью спроса от

цены.

На прак-

тике эластичность спроса от цены изучается применительно к основным потреби-

тельским товарам и товарным группам (например, мужская одежда). Эластич-

ность спроса от цены на отдельные конкретные изделия (например, швейные,

текстильные), продажа которых носит сезонный характер, неизвестна. В этой

связи

можно полагать, что сезонное снижение цен имеет характер игры торгового

предприятия

с природой.

Принятие

решения о размере снижения цен может рас-

сматриваться как поиск оптимальных цен в условиях неопределенности, что

предполагает возможность использования теории статистических игр.

Сущность

общая

структура

статистических

игр. Статистическая тео-

рия

игр является составной

частью

общей теории игр, представляющей собой

342

раздел современной прикладной математики, содержанием которой являются ме-

тоды обоснования оптимальных решений в конфликтных ситуациях.

Терминология,

которой пользуются в теории игр,

ведет

свое происхождение

от спортивных и азартных игр. Эти игры носят характер соревнования, которое

проводится по определенным правилам и заканчивается выигрышем

того

или

другого

игрока. В соответствии с этим и в теории игр стороны,

участвующие

игре, условно именуются игроками, а оценка

исхода

игры — выигрышем (или

проигрышем, платежом). При этом игроками

могут

быть как отдельные личнос-

ти,

так и целые коллективы людей, имеющих общие цели. В игре

могут

сталки-

ваться интересы

двух

и более

противников.

В первом

случае

игра называется пар-

ной,

во втором — множественной. Наиболее простой и теоретически разработан-

ной

является игра

двух

лиц с нулевой суммой. В этой игре

сумма

выигрышей

всех

оперирующих сторон равна нулю. Здесь один игрок выигрывает ровно

столько, сколько проигрывает второй.

Объектом нашего изучения является парная статистическая игра, базирую-

щаяся

на теории матричных игр

двух

лиц с нулевой суммой.

В теории статистических игр различают такие

понятия,

как исходная стратеги-

ческая игра и собственно статистическая игра. В этой теории 1-го игрока называют

природой,

под которой понимают совокупность обстоятельств, в условиях которых

приходится принимать решения 2-му игроку, называемому статистиком.

В стратегической игре как 1-й, так и 2-й игроки

действуют

активно,

оба заин-

тересованы выиграть, оба стремятся выбирать выгодные им стратегии. Для стра-

тегической игры характерна полная неопределенность в выборе стратегий каж-

дым игроком, т.е. каждый игрок ничего не знает о стратегии

другого.

В стратеги-

ческой игре оба игрока

действуют

на основе детерминированной информации,

определенной матрицей потерь.

В собственно статистической игре природа не является активно

действую-

щим

игроком в том смысле, что она не выбирает для себя

всегда

оптимальные

стратегии, так как не заинтересована выиграть

игру

и не оказывает противодейст-

вия

достижению цели 2-м игроком. Статистик (2-й игрок) в статистической игре

стремится выиграть

игру

у воображаемого противника

—

природы. Если в страте-

гической игре игроки

действуют

в условиях полной неопределенности, то для

статистической игры характерна частичная неопределенность. Дело в том, что

природа развивается и

"действует"

в соответствии со своими объективно

сущест-

вующими

законами.

У статистика есть возможность постепенно изучать эти зако-

ны

(на основе статистического эксперимента), выявлять механизм, который с

учетом

устанавливаемых вероятностей

реализует

разные состояния (стратегии)

природы.

Таким

образом, безразличие природы к игре и возможность получения ста-

тистиком в

ходе

соответствующего

статистического эксперимента дополнитель-

ной

статистической

информации

о состоянии природы отличают

игру

статистика

с природой от обычной стратегической игры, в которой принимают

участие

два

заинтересованных антагонистических противника.

Введем

обозначения:

—

множество состояний (стратегий) природы, £1«

(9i,...,

);

—

отдельное состояние (стратегия) природы (j « 1,

2,...,

к);

—

множество решений (стратегий) статистика, А - (ai,..., а

);

а|

—

отдельное решение статистика

(i»1,...Д);

343

L(9i, ai) - функция потерь (платежа) статистика или платежная матрица

с "к" строками и "1" столбцами. Функция потерь определяется

как

произведение множеств состояний природы и решений стати-

стика.

Исходная стратегическая игра обычно имеет три параметра (Q, A, L), так как

ее основу составляет детерминированная информация, определяемая функцией

потерь. Если статистик не имеет возможности провести эксперимент с целью по-

лучения дополнительной статистической информации о состоянии природы, то

при

принятии решения он

будет

ограничиваться исходной стратегической игрой.

Если

же статистик может провести статистический эксперимент и получить на

его основе дополнительную статистическую информацию о состоянии природы,

то функция потерь L(9i, ai) в исходной стратегической игре уже не

будет

удовле-

творять статистика как основа

принятия

решения.

Имея дополнительную

инфор-

мацию о состоянии природы, статистик при принятии решения

будет

руковод-

ствоваться какой-то функцией решения, и в

результате

исходная стратегичес-

кая

игра

(п.,

A, L) превращается в собственно статистическую

игру

(Q, Д, R). До-

полнительная

информация в собственно-статистической игре

выступает

в виде

вектора оценок X

(xi,

хг,...,

) состояний природы (9i,

...,-9

Заметим, что до-

полнительную статистическую информацию о состоянии природы статистик

может получить не только на основе собственного эксперимента (например, ан-

кетного опроса), но и на основе собственного опыта и интуитивного представле-

ния

о том, какие из состояний природы являются более правдоподобными, а

какие

— менее.

Статистик, получив дополнительную информацию о состоянии природы в

виде вектора оценок X = (xt, ... х

) состояний природы (9ь ... 9

), как отмече-

но

выше,

будет

теперь при принятии решения а е А руководствоваться какой-

то функцией решения d(x). Функция d(x), отображающая множество выбо-

рок

экспериментов X в множестве решений статистика А = (ai, аг, .... ai), на-

зывается нерандомизированной функцией решения статистика. Эта функция

показывает статистику, какое решение а е А он должен выбрать, когда наблю-

дается

результат

эксперимента х.

Существует

много функций решения d(x),

которыми мог бы воспользоваться статистик. Множество

всех

нерандомизиро-

ванных функций решения d(x), которое представляет собой множество

всех

стратегий статистика, обозначается через Д. Статистик ищет оптимальную

функцию

решения d e Д, которая

будет

его стратегией. Для сравнения различ-

ных функций решения и выбора из них наилучшей статистик должен знать их

характеристики и критерии выбора. Числовой характеристикой функции ре-

шения

d(x) является функция риска R(0, d), представляющая собой матема-

тическое ожидание функции потерь при некотором состоянии природы 0 и за-

данной

функции условного распределения случайной переменной ХР (х/0),

так

как а = d(x). Для фиксированного состояния природы 9 и выбранной

функции

решения d € Д риск R(0, d) играет роль платежа в игре статистика с

природой.

Этот платеж

будет

средней потерей статистика, если многократно использу-

ется функция решения d е Д, а природа принимает состояние 9 е П.

Функция

риска определяется как произведение Q х Д (множества состояний

природы и множества функций решения). Для каждой нерандомизированной

344

функции

решения d

е Д риск для каждого состояния природы 8j (j = 1,

2,...,

к)

определяется по формуле:

где

P[xi|8j}

—

условная вероятность

оценки

при

состоянии

природы 0j (i

=1,2,...,

—

1, 2y.

к).

в матрице функции риска

R(9,d)

ведется поиск минимальной страте-

гии,

для

чего

в каждом столбце матрицы отыскивается наибольший элемент, а

затем среди них выбирается минимальный. Столбец с этим минимальным эле-

ментом указывает искомое решение статистика в зависимости от

результата

экс-

перимента.

Пример.

Торговое предприятие имеет 500 нераспроданных женских летних

платьев, средняя цена которых равна 200 руб., а затраты на их приобретение у

производителя сооставили 120 руб. Предприятие знает, что мода на такой товар

быстро меняется, и в

будущем

можно не найти на него покупателей. Если платья

вовремя не продать, то увеличатся торговые запасы и издержки. Предприятие ре-

шает снизить цены, чтобы вызвать дополнительный спрос на платья. Однако ре-

шение о размере снижения цен при сезонной распродаже товаров должно быть

обдуманным, чтобы потери торгового предприятия были минимальными. Пред-

приятие решает рассмотреть четыре варианта снижения цены

—

на

20,30,40,50%.

При

этом оно должно

учитывать

предполагаемую реакцию покупателей на сезон-

ное снижение цен, которая измеряется эластичностью спроса от цены, показы-

вающей, на сколько процентов в среднем возрастает спрос на товар, если цена его

снижена на 1%. Эластичность спроса от цены определяется по формуле:

о=

где Э — эластичность спроса от цены;

— спрос на товар при заданной цене (Ц) на него;

АЦ

—

абсолютное изменение цены;

АК — прирост спроса на товар при снижении цены на него на величину АЦ.

Итак,

требуется

определить оптимальный размер снижения цены на платья,

при

котором потери торгового предприятия

будут

минимальными.

В рассматриваемой

задаче

в качестве 2-го игрока (статистика)

выступает

торговое предприятие. В качестве 1-го игрока (природы)

—

реакция покупателей

на

изменение цены на рассматриваемые платья, т.е. эластичность спроса от цены,

о которой торговое предприятие в данный момент знает лишь то, что этот спрос

на

платья может быть как малоэластичным, так и высокоэластичным. Каким в

Действительности является этот спрос, предприятие не знает, однако может вы-

явить его либо на основе

результатов

экспресс-опроса, либо в

информации,

полу-

ченной на основе ранее проведенных наблюдений и расчетов. В качестве показа-

телей, характеризующих стратегию природы,

выступает

распределение вероят-

ностей, с которыми природа применяет отдельные свои стратегии

(малую

и высо-

кую эластичность спроса). Следовательно, сезонное снижение цен имеет характер

345

игры торгового предприятия с природой и может определяться на основе теории

статистических игр.

Составим

структуру

статистической игры,

соответствующую

проблеме се-

зонного снижения цен.

Введем

обозначения:

—

множество возможных состояний природы, включающее два Q

}

элемента, где 0i

соответствует

малоэластичному спросу на данную

группу

одеж-

ды при изменении цены, а 0

означает, что эластичность спроса от цены высокая;

А — множество возможных решений торгового предприятия, включающее

четыре элемента: А = {а^ а

, аз, ад}, где at — решение снизить цену на данный

товар в среднем на 20%; а

— на 30%; аз

—

на 40%; а

—

на 50%;

L(0, a) — функция потерь торгового предприятия, которая имеет конечное

число 2x4 значений.

Каждый элемент этой функции потерь определяется на основе

следующих

данных:

1) количество не распроданных платьев

—

500 шт.;

2) закупочная цена товара

—

120 руб.;

3) продажная цена товара

—

200 руб.;

4) решение торгового предприятия о снижении продажной цены на

20,30,40,

50%;

5) коэффициенты эластичности при малой эластичности спроса от цены на

аналогичные товары принимаем в размере 1; 1; 1,1; 1 и при высокой эластичности

спроса от цены в размере 1,5; 2,33; 2; 1,8;

6) предполагаемый объем продажи платьев (шт.) в

результате

снижения цен

(его надо определить).

Предполагаемый объем продажи платьев в

результате

снижения цены опре-

деляется по формуле эластичности спроса от

цены,

которая имеет вид:

дк.дц

К ' Ц

Откуда:

ДК

(Э

х К) х —•

Поскольку -ц-

т.е. проценту снижения цены, то предполагаемый объем

продаж ДК| (i

l,l;j

1,2) в зависимости от

коэффициента

эластичности Э; (j « 1,2)

может быть вычислен по формуле:

(Заметим, что если правая часть этого равенства станет больше К, то принимаем

ДК - К).

При

состоянии природы 0] и 0

значения функции потерь для решений ai,

аг. а

вычисляются как разность

между

закупочной стоимостью нераспродан-

ных 500 платьев и выручкой от предполагаемого объема продаж после снижения

цен.

Представим соответствующие расчеты в табл. 5.28 и 5.29 применительно к

состоянию природы 0] и 0

346

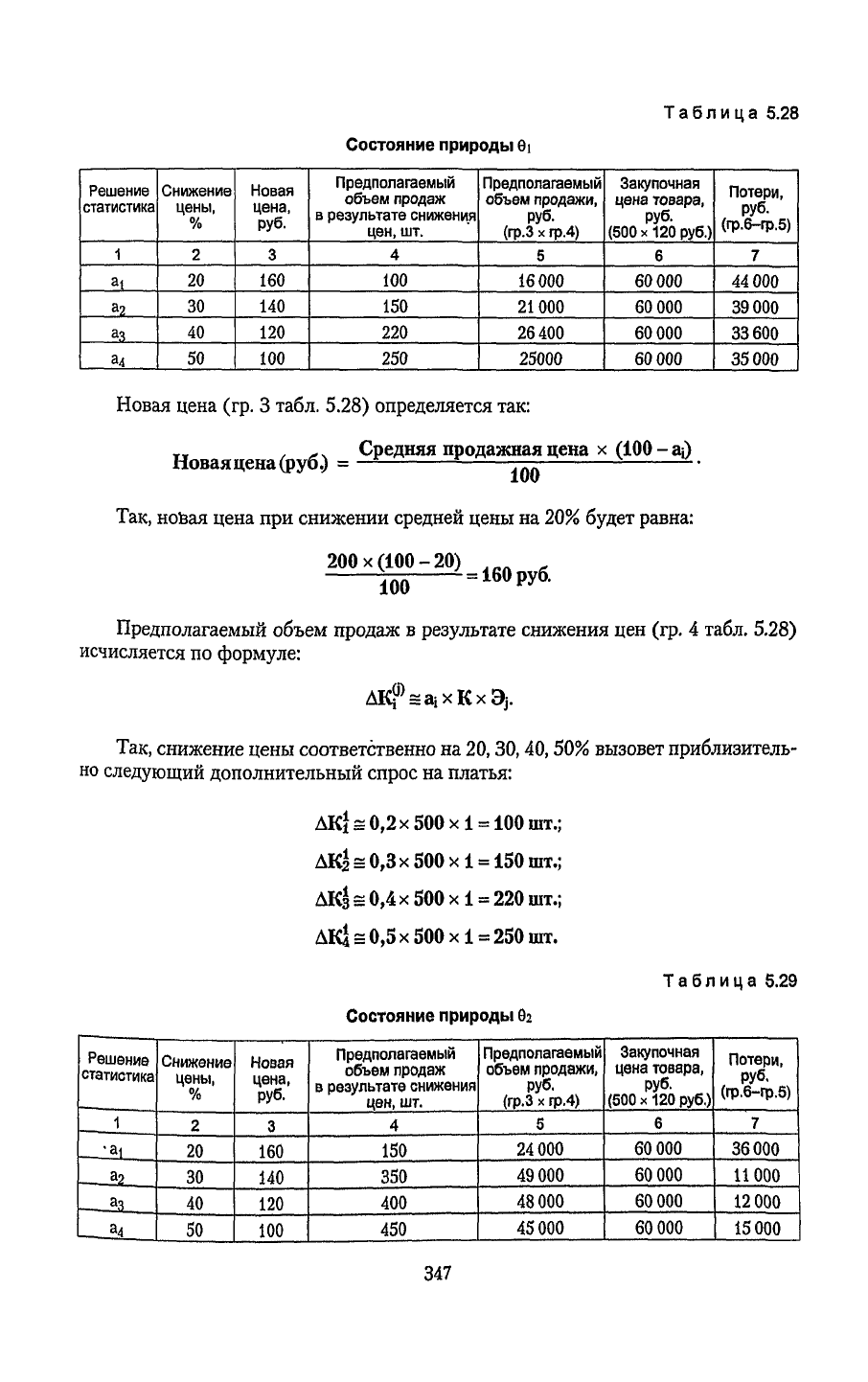
Таблица

5.28

Состояние природы Gi

Решение

статистика

Снижение

цены,

Новая

цена,

руб.

160

140

120

100

Предполагаемый

объем продаж

в результате снижения

цен,

шт.

100

150

220

250

Предполагаемый

объем продажи,

руб.

(гр.З

гр.4)

16000

21000

26400

25000

Закупочная

цена товара,

руб.

(500x120 руб.)

60000

60 000

Потери,

руб.

(ф.б-гр.5)

000

39000

600

35000

Новая цена (гр.

табл.

5.28)

определяется

так:

Новая

цена

(руб.)

Средняя

продажная

цена

(100

ар

100

Так, новая цена при снижении

средней

цены на 20%

будет

равна:

200

(100-20)

100

160

руб.

Предполагаемый

объем

продаж

результате

снижения цен (гр.

табл.

5.28)

исчисляется по

формуле:

Так, снижение цены

соответственно

на

20,30,40,50%

вызовет

приблизитель-

но

дополнительный спрос на платья:

0,2 х 500

100

шт.;

0,Зх

500x1

150

шт.;

0,5x500x1

250 шт.

Состояние природы

Таблица

5.29

Решение

статистика

•а,

*2__

—5з__

Снижение

цены,

Новая

цена,

руб.

160

140

120

100

Предполагаемый

объем продаж

в результате снижения

цен,

шт.

150

350

400

450

Предполагаемый

объем продажи,

руб.

(гр.З

х гр.4)

24000

49000

48000

45000

Закупочная

цена товара,

руб.

(500

120

руб.)

60 000

60000

60 000

Потери,

руб.

(гр.6-гр.5)

36000

11000

12 000

15000

347

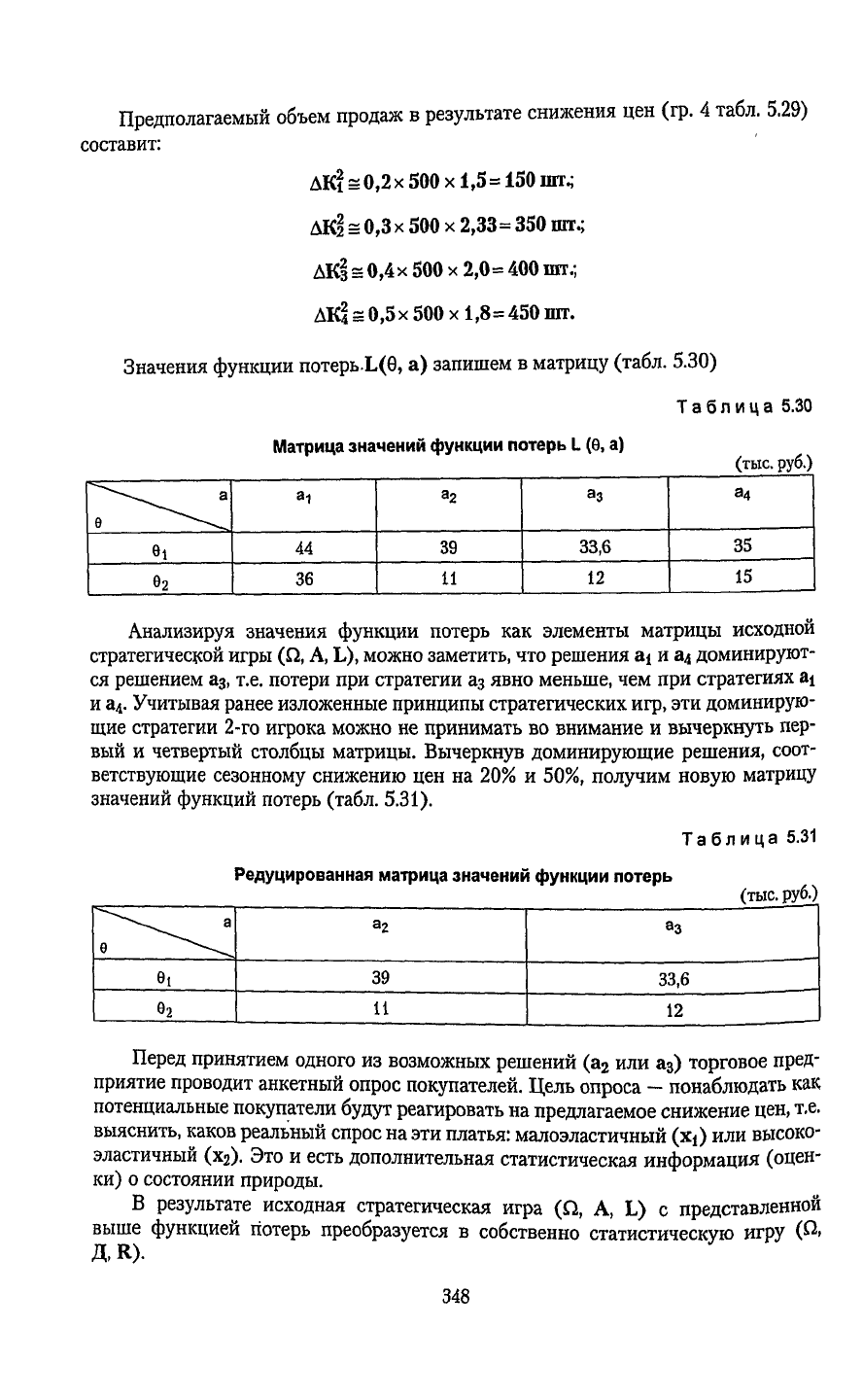
Предполагаемый объем продаж в

результате

снижения цен (гр. 4 табл. 5.29)

составит:

ДК? =

0,2 х 500 х 1,5= 150 шт.;

ЛК1 =

0,3 х 500 х 2,33= 350 шт.;

ДК|

s 0,4 х 500 х 2,0= 400 шт.;

ДК|

£ 0,5 х 500 х

1,8=450

шт.

Значения

функции потерь.Цб, а) запишем в матрицу (табл. 5.30)

Таблица

5.30

Матрица

значений

функции

потерь L

(6,

а)

(тыс. руб.)

~^~-^

--^

аз

33,6

Анализируя значения функции потерь как элементы матрицы исходной

стратегической игры

(Q,

L),

можно заметить, что решения aj и 34 доминируют-

ся

решением аз, т.е. потери при стратегии аз явно меньше, чем при стратегиях ai

и ац.

Учитывая ранее изложенные

принципы

стратегических

игр,

эти доминирую-

щие стратегии 2-го игрока можно не принимать во внимание и вычеркнуть пер-

вый и четвертый столбцы матрицы. Вычеркнув доминирующие решения, соот-

ветствующие

сезонному снижению цен на 20% и 50%, получим новую матрицу

значений

функций потерь (табл.

5.31).

Таблица

5.31

Редуцированная

матрица

значений функции

потерь

(тыс. руб.)

^~~^^^

аз

33,6

Перед принятием одного из возможных решений (аг или аз) торговое пред-

приятие

проводит анкетный опрос покупателей. Цель опроса — понаблюдать как

потенциальные покупатели

будут

реагировать на предлагаемое снижение

цен,

т.е.

выяснить,

каков реальный спрос на эти платья: малоэластичный (xi) или высоко-

эластичный (х

). Это и есть дополнительная статистическая информация (оцен-

ки)

о состоянии природы.

результате

исходная стратегическая игра (ft, A, L) с представленной

выше функцией потерь преобразуется в собственно статистическую

игру

(^>

ДК).

348

При

проведении анкетного опроса покупатели должны ответить, к примеру,

на

вопрос: "При каком размере снижения цены (30, 40%) Вы не купили бы пла-

тье?

Не устраивающее Вас значение подчеркните". Результаты опроса

будут

иметь вид двумерного множества X = {xi, х

}, где xj — низкая оценка, а х

— вы-

сокая

оценка эластичности спроса от цены. Например, представим, что результа-

ты опроса показали, что на снижение цены на 30% согласны 10% опрошенных, на

снижение цены на 40%

—

также 10%. Остальные 80% опрошенных не подчеркну-

ли ни одно число, т.е. практически отказались от

покупки.

Вывод: спрос на платья

результате

предполагаемого снижения цен оказался малоэластичным.

Торговое предприятие при принятии решения о сезонном снижении цен

должно учитывать полученную в

результате

опроса информацию о спросе.

Учитывая возможность ошибок при проведении единовременного анкетного

опроса случайно отобранных покупателей, примем следующие условные распре-

деления результатов x

и х

в зависимости от действительного состояния приро-

ды 8i и 02, т.е. от мало- или высокоэластичного спроса:

P{xi|G

}

0,7; Р {X!

[

}

0,2;

Р{х

}

ОД Р{х

|е

}

0,8.

Приведенные условные распределения результатов xi и х

в зависимости от

действительного состояния природы 0л и 0

являются априорными величина-

ми,

полученными на основе многих ранее проведенных наблюдений.

учетом

двух

возможных экспериментальных значений оценок xi и х

ко-

торым соответствует одно из

двух

допустимых решений торгового предприятия

—

или аз, множество нерандомизированных функций

будет

состоять из четырех

элементов, т.е. число элементов множества Д = {di, d

, d3, d

}. Нерандомизиро-

ванные функции для значений оценок xi и х

приведены в табл. 5.32.

Таблица 5.32

Нерандомизированные

функции

а2

аЗ

аз

аг

аз

Нерандомизированные функции с

учетом

результатов эксперимента, как

было-указано выше, помогают выбрать то или иное решение. Например, функция

<1з

означает, что нужно принять решение аз, если результатом эксперимента яв-

ляется xi, и решение а

, если результатом эксперимента является х

. Для каждой

из

этих четырех нерандомизированных функций решения можно с

учетом

обоих

состояний природы 01 и 0

вычислить значения функции риска R(0, d). Функ-

ция

риска R(0, d) определяется по формуле:

349

Для 9i и di получим R(9

di) = 39 x 0,7 + 39 x 0,3 - 39. Функция решения

di как

результату

эксперимента xi, так и

результату

приписывает решение

аз,

которое при действительном состоянии природы 6i обусловливает потерю

39 тыс. руб., причем соответствующие этому состоянию природы условные веро-

ятности

результатов

xi и хг составляют 0,7 и 0,3.

Вычислим остальные значения функции риска:

R(Gi, d

) - 39 х 0,7

33,6 х 0,3 - 37,38;

R(6i, ds)

33,6 x 0,7

39 x 0,3

35,22;

R(6i, d

)

33,6 x 0,7

33,6 x 0,3

33,6;

R(e

, di) = ii x 0,2

+11

x 0,8

«11,0;

R(02, d

)

11 x 0,2 +12 x 0,8

11,8;

R(6

, d

)

12 x 0,2

11 x 0,8

11,2;

R(e

, d

)

12 x 0,2 +12 x 0,8

12,0.

Значения

функции риска R(9, d) запишем в матрицу (табл.

5.33).

Таблица

5.33

Матрица

значений

функции

риска

(8j

^~-\^^ d

^^~~^^

37,38

11,8

35,22

11,2

33,6

Для этой матричной игры находим оптимальное решение. Оптимальным

будет

такое решение о размере сезонного снижения цен на летние платья, которое

максимально защищает торговое предприятие от высоких потерь. Наиболее осто-

рожной функцией решения

будет

минимаксная стратегия статистика. Выбираем

для каждого столбца матрицы значений функции риска максимальный элемент, а

затем среди них — минимальный элемент и тем самым определяем столбец di с

этим минимальным элементом.

В решаемой

задаче

среди максимальных элементов минимальным является

число 33,6. Этому числу

соответствует

нерандомизированная минимаксная функ-

ция

решения di.

Поскольку эта функция определялась при условии, что

di(xi)

аз и

d4(x

)

аз.

то в данном

случае

оптимальной, т.е. наиболее осторожной, стратегией торгового

предприятия, намечающего сезонное снижение цен на летние женские платья,

будет

стратегия снижения цен на 40%. Это относится к

случаю,

когда по резуль-

татам анкетирования спрос оценивался как малоэластичный, так и к

случаю,

когда оценка указывала на высокоэластичный спрос.

350