Baker R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications

Подождите немного. Документ загружается.

5.2 ESSENTIAL BACKGROUND EQUATIONS 97

for those concerned with the design, installation, and maintenance of orifice plate

meters.

5.2 ESSENTIAL BACKGROUND EQUATIONS

Mass Flow Rate Equation

The mass flow rate is related to the differential pressure by the equation (c.f. Equa-

tion 2.11 for flow without loss)

= f (5.1)

where C is the coefficient of discharge, E is the velocity of approach factor

(1 -

1/2

where p is the diameter ratio d/D of orifice diameter to pipe internal

diameter, e is the expansibility (or expansion) factor, Ap is the differential pressure,

and pi is the density at the upstream pressure tapping cross-section. The value of

the volumetric flow can be obtained from this using the relationship:

<7v

= q

/p (5.2)

where p is the density of the fluid at the appropriate conditions of pressure and

temperature.

Coefficient of Discharge

A simple expression for the discharge coefficient is

Coo +

(5>3)

where C^ is the coefficient for infinite Reynolds number, C

is a constant for a par-

ticular installation, Re is the Reynolds number based on the pipe internal diameter,

and n is the index to which this is raised. The relative simplicity of Equation 5.3

is not matched by the most commonly used expressions for C, C^ or C

either in

their complexity or variety.

The development of the equation commonly referred to as the API or AGA equa-

tion can be found by referring to Bean (1971) and Spitzer (1991). Reader-Harris and

Sattary (1990, cf. Reader-Harris 1989) reported that a joint meeting of European

Community and American Petroleum Institute (API) flow measurement experts in

New Orleans in November 1988 unanimously accepted a new equation. API 2530

was revised to include the Reader-Harris/Gallagher equation. This allowed for an

additional term for small pipes. Additional data have now allowed an adjustment

to the equation for small orifice diameters. This was reported by Reader-Harris et al.

(1995).

The previous coefficient of discharge adopted by the ISO and British Standards

Institution was given by an equation due to Stolz (1978, 1988). This equation was

retained in the standard until 1998. For details of the thorough work that has taken

place in the last 10 years or so, the reader is referred to Reader-Harris et al. (1995)

and Spencer (1993) (cf. Fling and Whetstone 1985).

98 ORIFICE PLATE METERS

The result is that current American practice appears to be to use API Chap-

ter 14 Section 3 (14.3) and a new expression for the discharge coefficient C has

been adopted by ISO, the Reader-Harris/Gallagher equation. However, the reader is

advised to refer to the document most appropriate to the application.

The form of these new equations is

C = Coo + jT-fi + Craps + Csmall orifice (5.4)

where all coefficients are functions of p. Craps includes values of L\ = l\/D and l\

is the distance of the upstream tapping from the upstream face of the plate, and

and

is the distance of the downstream tapping from the downstream

face of the plate. The prime signifies that the measurement is from the downstream

and not the upstream face of the plate. C

reflects the slope of the characteristic due

to change of Re.

I have decided to include the provisional form of the equation in Appendix 5.A.

However, it is essential that the reader refers to the standard document to check

the latest version adopted in the United States, United Kingdom, or elsewhere and

to obtain all the conditions necessary for its valid use. These include ranges for

parameters, detailed design, pipe smoothness, etc.

The data for the new equation appear to have been obtained for orifice plates with

diameter ratios 0.1-0.75, throat Reynolds numbers from 1700 to 5 x 10

, and pipe

diameters from 50 to 250 mm. Data points for orifice diameters less than 12.5 mm

were very scattered and were not included.

The uncertainty is in the range 0.5-0.75% for D > 71.12 mm, and the precise

value depends on p. For small orifices, an additional uncertainty is combined arith-

metically and can be of order 0.4% for D = 25.4 mm (1 in.).

Miller (1996) gave the proposed Stolz II and NEL/TC 28 equations and tabulated

the values for these compared with ISO and

ANSI/API.

Perusal of the variation across

all equations is quite instructive.

difference between the new equations of at least

0.15%

is quite common, with differences occasionally as high as 1% for Re = 5,000.

Comparison of both old and both new gives a spread of discharge coefficients of

less than 0.1% to nearly 2%. The best agreement appears to be for p = 0.5 and

Re > 10,000, where variation across all four equations is less than 0.1% to about

0.5%.

One benefit, therefore, of the extensive work on refining equations has been

to increase our confidence in existing values of the discharge coefficient and in

indicating where the main divergences from these occur. Spitzer, also, makes the

point that the actual maximum variation in discharge coefficient obtained from the

main equations for a range of Reynolds numbers from 20,000 to 2,000,000 is only of

order 0.12%. For a p

0.5,

Re = 10

, and corner tappings, I estimate that the value of

C for the latest version of ISO is about 0.13% greater than for Stolz, which generally

confirms Spitzer's comments.

Expansibility Factor

The expansibility (expansion) factor provides an adjustment factor to allow differen-

tial pressure devices to be calibrated on water, an essentially incompressible fluid for

these purposes, for use on compressible gas. It, essentially, provides an adjustment

factor to the coefficient of discharge that allows for the compressibility of the gas.

5.2 ESSENTIAL BACKGROUND EQUATIONS 99

Reader-Harris (1998) provides a review of the past development of this factor and

the current recommended equation for it. It is found to be virtually independent of

Reynolds number. For many years, it was given by an equation of the form:

l =

l-(a

€

)^- (5.5)

where a

€

and b

€

are constant coefficients, K is the isentropic exponent, which for

an ideal gas is equal to y, the ratio of specific heats, and if K is not known y

should be used, pi is the pressure at the upstream tapping. However, according to

Kinghorn (1986) the coefficients in common use in Equation (5.5) were probably in

error.

In the most recent version of the standard, a new equation for e

is given but

may be due for a further update. It is of the form

(5.6)

provided that pi/pi > 0.75. c

€

is another constant coefficient. The final bracket may

be approximated by Ap/icpi if

P2/P1

is very close to unity, but the work of Reader-

Harris (1998) suggests that the expression in the final bracket is preferable. He gave

the following equation, following careful analysis of the data, which may now be in

the latest ISO standard:

€i = l- (0.351 + 0.2S6p

+ 0.93£

)| 1 - (^) \ (5.7)

He gave a relative uncertainty for e\ of 3.5Ap/Kpi %, which differs slightly in de-

tail from that in

ISO.

He also gave

very useful theoretical derivation and obtained an

equation that differs from Equation (5.7) by about the uncertainty in Equation (5.7).

Pressure Loss

The expression in the ISO standard for the pressure loss across the orifice plate now

appears to be

Pressure

loss.

^jg^-C^

Jlp\\C

) +

Taking a typical value of C of about 0.6, this results in a pressure loss for a plate

with p = 0.5 (and E =

1.033)

of about 0.73Ap [cf. Urner 1997 who suggested that

the previous ISO equation (for nozzles and orifice plates) gives anomalous results if

used outside the limits of applicability of the ISO standard].

An alternative for orifice plates allowed by a recent version of the standard is

Pressure loss « (1 -

)Ap

(5.9)

which, for the preceding case, also gives 0.73Ap.

The most recent version appears to have provided a loss coefficient K given by

K = **»»*

1OSS

(5.10)

^PV

100 ORIFICE PLATE METERS

where

One of the most welcome changes in the latest version of the standard is the elimi-

nation of the symbol a, the flow coefficient, which was of little value. It has been

replaced by

CE,

to which it was equal, or other equivalent expression.

5.3 DESIGN DETAILS

Design details are set out fully in the ISO 5167 standard. It is important that the

detailed requirements are followed so that performance can be predicted, but also

so that new data can be added to existing data, to increase our overall knowledge.

In this book, some of the requirements will be touched on, but the standard should

be referred to for full details.

The design is, of necessity, an iterative procedure starting from the known re-

quirements of, typically, design flow rate, pipe size, and differential pressure. Danen

(1985) gives some helpful calculation flowcharts for each type of differential meter.

The first educated guess will relate to the value of p. With this and the selected values,

a new value of p is found via the flow rate equation. Iteration continues until a satis-

factory value of p is achieved. However, it is likely that most users will have access to

a computer program for this procedure (either from a manufacturer or in their own

software library) that will enable the optimum size of plate to be obtained. These

will ensure a balance between too great a pressure drop through the plate and too

small a differential pressure for measurement. It is often suggested (Miller 1996) that

the pressure drop across the orifice plate should be of the order of 100 in. of water

(2.5 m or 25 kPa) and that the beta ratio should be close to 0.5. In some cases, this

may not be achievable. The pressure loss can never exceed the difference between

supply and demand pressures, and the minimum pressure should be kept above the

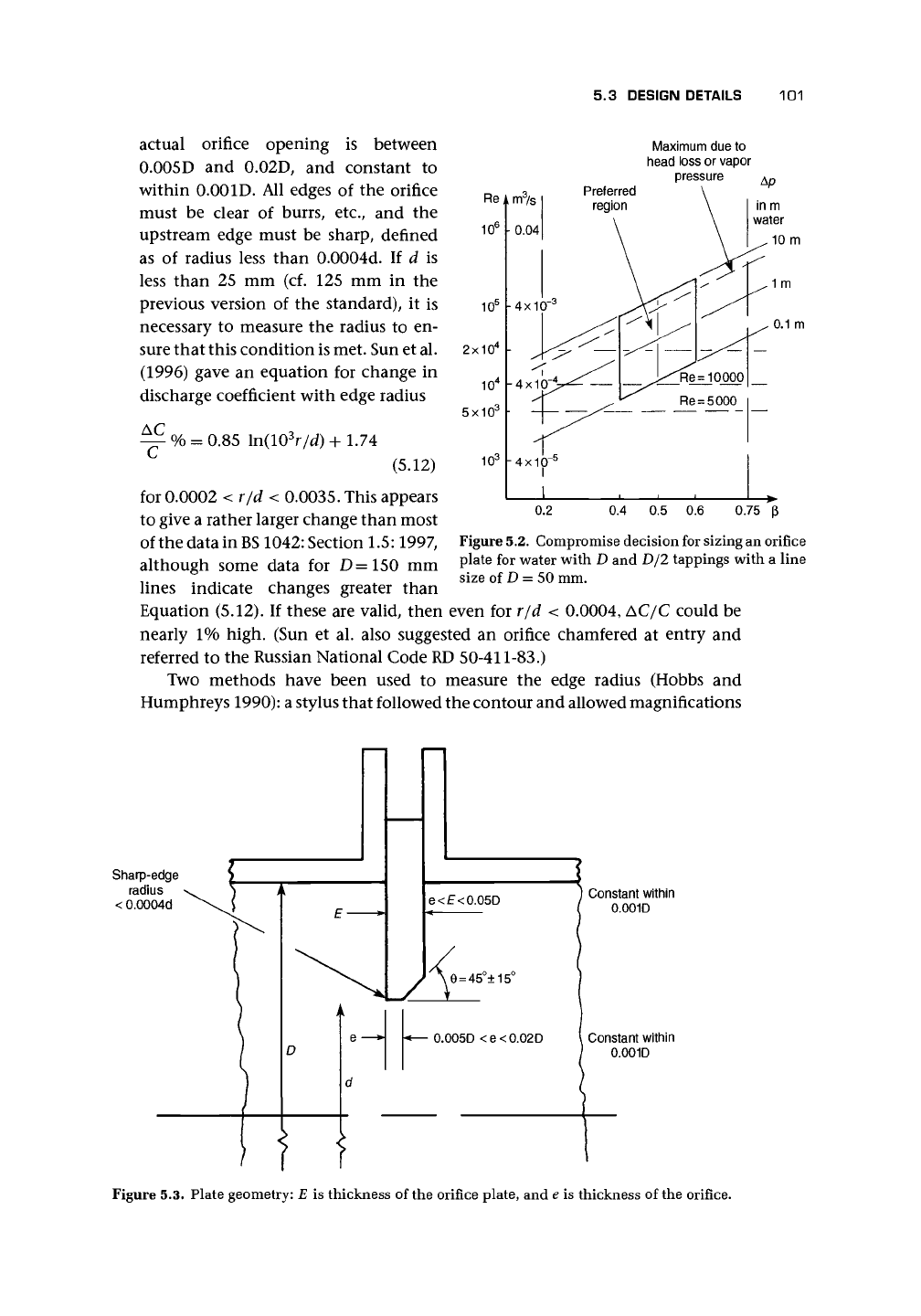
liquid's vapor pressure to avoid cavitation. Figure 5.2, which has been suggested in

various forms by various people, illustrates the compromise decision that needs to

be made between these factors.

For wide-range metering, Miller suggests the use of two transmitters ranged for

180 in. of water (4.5 m and 45 kPa) and 20 in. of water (0.5 m and 5 kPa).

a. The plate. Some details of the plate geometry are shown in Figure 5.3 for a pipe of

diameter D and with an orifice diameter of

The plate must be flat with parallel

faces,

and concentric. Flatness is defined in the standards. The upstream face is

the most critical because this has a strong effect on the flow entering the orifice.

In addition to the flatness, the plate must have a roughness of less than 10~

It is useful to indicate the correct flow direction on the plate in a position that

can be seen when the plate is installed. The plate may have to be rather thick to

withstand the forces due to the flow, and in this case the downstream edge of

the orifice is beveled at an angle of 45° ± 15°, so that the final thickness of the

5.3 DESIGN DETAILS

101

actual orifice opening is between

0.005D and 0.02D, and constant to

within 0.001D. All edges of the orifice

must be clear of burrs, etc., and the

upstream edge must be sharp, defined

as of radius less than 0.0004d. If d is

less than 25 mm (cf. 125 mm in the

previous version of the standard), it is

necessary to measure the radius to en-

sure that this condition is met. Sun et al.

(1996) gave an equation for change in

discharge coefficient with edge radius

^ % = 0.85 ln(10

r/d) + 1.74

(5.12)

for 0.0002 < r/d < 0.0035. This appears

to give a rather larger change than most

of the data in

1042: Section 1.5:1997,

although some data for D=150 mm

lines indicate changes greater than

Preferred

region

Maximum due to

head loss or vapor

pressure

in m

water

10 m

0.1 m

Figure 5.2. Compromise decision for sizing an orifice

plate for water with D and D/2 tappings with a line

size of D = 50 mm.

Equation (5.12). If these are valid, then even for r/d < 0.0004, AC/C could be

nearly 1% high. (Sun et al. also suggested an orifice chamfered at entry and

referred to the Russian National Code RD 50-411-83.)

Two methods have been used to measure the edge radius (Hobbs and

Humphreys 1990): a stylus that followed the contour and allowed magnifications

Sharp-edge

radius

< 0.0004d

e<£<0.05D

• 0.005D <e<0.02D

Constant within

0.001D

Constant within

0.001D

Figure 5.3. Plate geometry: E is thickness of the orifice plate, and e is thickness of the orifice.

102 ORIFICE PLATE METERS

Flange

tappings

Pressure

tappings

(b)

(c)

Carrier

ring with

annular

slot

of up to 500, and a cast around the

edge which could be sliced and polished

after removal from the edge. Results

to 0.005 mm are claimed (cf. Jepson

and Chamberlain 1977 who described

British Gas's orifice radius inspection

system).

Pressure

tappings.

There are three stan-

dard methods of sensing the pres-

sure drop across the orifice plate

(Figures 5.1 and 5.4): D and D/2

tappings (Figure 5.1), flange tappings

(Figure 5.4), and corner tappings (Fig-

ure 5.4).

Again the standards set out the pre-

cision of positioning of the tappings

and the details of their manufacture (cf.

Zedan and Teyssandier 1990, who con-

cluded that the tolerances that ISO and

ANSI/API 2530 allowed for pressure tap

locations were conservative).

5.4 INSTALLATION CONSTRAINTS

The upstream and downstream pipe lengths

are set out in some detail in ISO

5167-1.

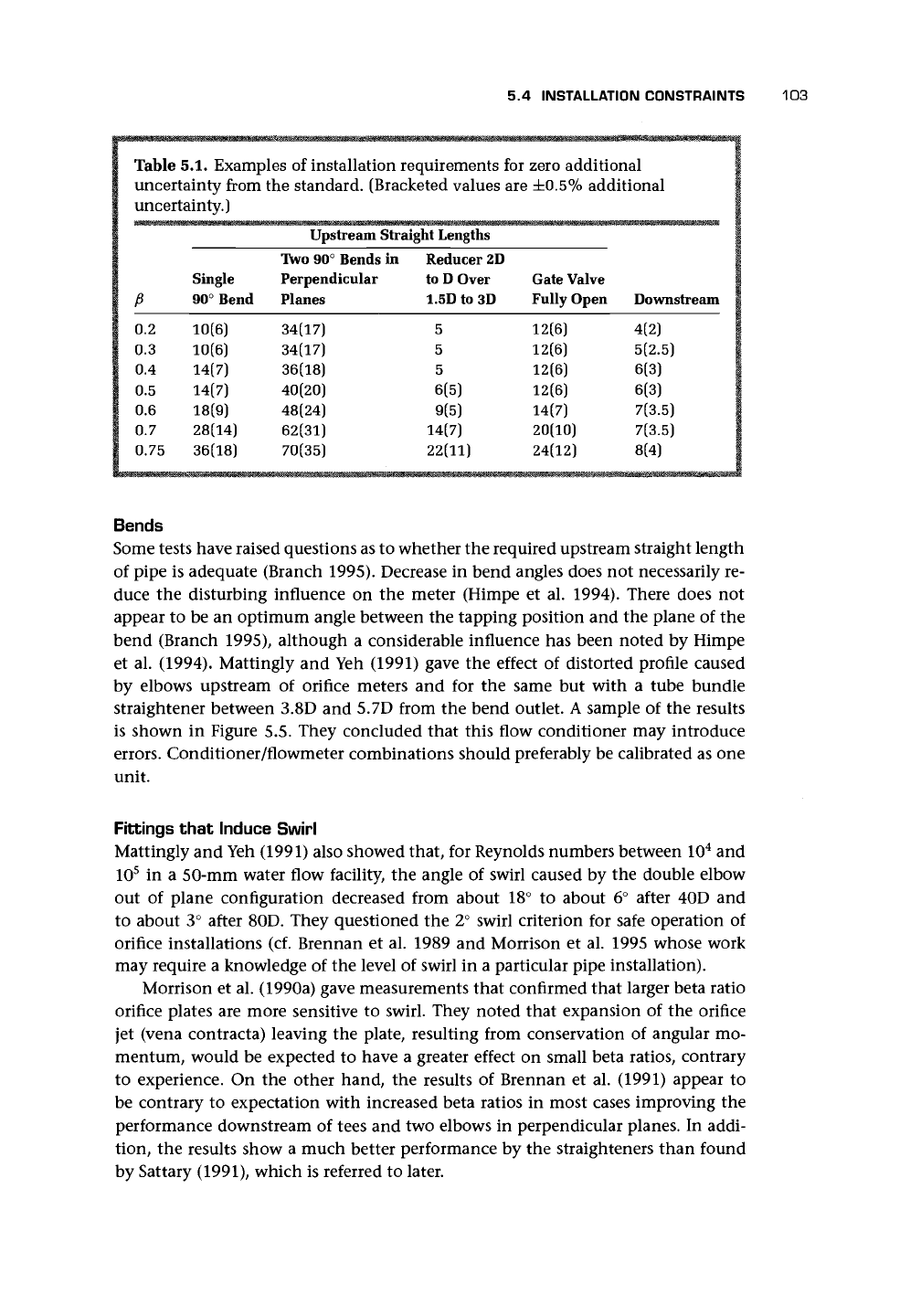
A sample of the information is given in

Table 5.1. The values given are claimed to

retain the predicted performance of the ori-

fice plate, whereas the values in parenthe-

ses increase the measurement uncertainty

0.5%.

For instance, a meter with ft = 0.5

mounted within 14D of

90° bend but with

more than 7D clear pipe upstream and 3D

downstream will have an uncertainty in the

coefficient of 0.6 + 0.5 = 1.1%.

Reader-Harris and Keegans (1986) sug-

gested that 2.5D of smooth pipe upstream

of corner tappings reduced the effect of pipe roughness further upstream. Sindt

et al. (1989) found up to 1% change in coefficient for p = 0.74 and Re = 7 x 10

between smooth (2.8 /xm) and rough (8.9 /xm), but for p = 0.5, the change was not

measurable.

Constraints are also placed on thermometer pockets near to the flowmeter.

The validity of these values is based on many tests to obtain data. Some recent

measurements are compared later.

Figure 5.4. Layout of pressure tappings (after ISO

5167-1): (a) Flange; (b) Corner

—

ring with annular

slot; (c) Corner

—

individual tappings.

5.4 INSTALLATION CONSTRAINTS

103

Table 5.1. Examples of installation requirements for zero additional

uncertainty from the standard. (Bracketed values are ±0.5% additional

uncertainty.)

""""

1 0.2

1 0.3

1 0.4

1 0.5

0<6

1 0.7

| 0.75

Single

90° Bend

10(6)

10(6}

14(7)

18(9)

28(14)

36(18)

Upstream Straight Lengths

Two 90° Bends in

Perpendicular

Planes

34(17)

36(18)

40(20)

48(24)

62(31)

70(35)

Reducer 2D

to D Over

1.5D to 3D

6(5)

9(5)

14(7)

22(11)

Gate Valve

Fully Open

12(6)

14(7)

20(10)

24(12)

Downstream

4(2)

5(2.5)

6(3)

7(3.5)

8(4)

Bends

Some tests have raised questions as to whether the required upstream straight length

of pipe is adequate (Branch 1995). Decrease in bend angles does not necessarily re-

duce the disturbing influence on the meter (Himpe et al. 1994). There does not

appear to be an optimum angle between the tapping position and the plane of the

bend (Branch 1995), although a considerable influence has been noted by Himpe

et al. (1994). Mattingly and Yeh (1991) gave the effect of distorted profile caused

by elbows upstream of orifice meters and for the same but with a tube bundle

straightener between 3.8D and 5.7D from the bend outlet. A sample of the results

is shown in Figure 5.5. They concluded that this flow conditioner may introduce

errors.

Conditioner/flowmeter combinations should preferably be calibrated as one

unit.

Fittings that Induce Swirl

Mattingly and Yeh (1991) also showed that, for Reynolds numbers between 10

and

in a 50-mm water flow facility, the angle of swirl caused by the double elbow

out of plane configuration decreased from about 18° to about 6° after 40D and

to about 3° after 80D. They questioned the 2° swirl criterion for safe operation of

orifice installations (cf. Brennan et al. 1989 and Morrison et al. 1995 whose work

may require a knowledge of the level of swirl in a particular pipe installation).

Morrison et al. (1990a) gave measurements that confirmed that larger beta ratio

orifice plates are more sensitive to swirl. They noted that expansion of the orifice

jet (vena contracta) leaving the plate, resulting from conservation of angular mo-

mentum, would be expected to have a greater effect on small beta ratios, contrary

to experience. On the other hand, the results of Brennan et al. (1991) appear to

be contrary to expectation with increased beta ratios in most cases improving the

performance downstream of tees and two elbows in perpendicular planes. In addi-

tion, the results show a much better performance by the straighteners than found

by Sattary (1991), which is referred to later.

104

ORIFICE PLATE METERS

• /

i i i i i

Beta

D 0.363

0 0.50

0.75

i i i i i i

(a)

8 16

Pipe diameters from

elbow outlet

3.0

2.0 -'

.£ 1.0

0.0

-1.0 -

•

"V,

Beta

Q 0.363

0 0.50

0.75

(b)

50 100

Pipe diameters from

double elbow outlet

.£

O -1.0

-2.0

(aa)

20 40 60

Pipe diameters from downstream

end of flow conditioner

(bb)

50 100

Pipe diameters from downstream

end of flow conditioner

Figure 5.5. Change in orifice coefficient when downstream of (from Mattingly and Yeh 1991

reproduced with permission of Elsevier Science): (a) Single elbow; (b) Closely coupled double

elbows out of plane; (aa) Single elbow with a tube bundle straightener; (bb) Closely coupled

double elbows out of plane with a tube bundle straightener.

Other Profile Distortions

Yeh and Mattingly (1994) measured the profile downstream of a reducer (approxi-

mately 3:2), and the effect of the reducer on the coefficient of an orifice plate flow-

meter. Their results appeared to confirm the ISO values for

= 0.5 and less, but not

for p

—

0.75 [cf. Morrison et al. 1992 who distorted the inlet profile to an orifice

plate by varying the ratio of flow in the outer (wall) area of the pipe to that flowing

through the center of the

pipe].

Flow Conditioners

McFaddin et

al.

(1989) found that, for a 100-mm (4-in.) line, a 2.5D long tube bundle

flow conditioner (19 x 12 mm tubes) 7D upstream of the orifice with fi = 0.75, the

minimum distance specified in the ANSI/API 2530 standard, the error can be as much

as 1%.

Kinghorn et al. (1991) found that the flat profiles downstream of etoile straight-

eners appeared to cause most of the residual negative errors in the orifice coefficient,

5.4 INSTALLATION CONSTRAINTS 105

as opposed to the positive errors due to swirling flow. To ensure an error of less than

±0.5%,

a straightener ID long should be placed upstream at least

• 6D for plates with a beta ratio of 0.5 and

• 14D for plates with a beta ratio of 0.8.

Even with 16D separation, virtually all tests suggested some effect from the straight-

ener.

Karnik et al. (1994) tested the effect of a 19-tube bundle in a 101.6-mm line

for good flow conditions and downstream of an elbow and looked at the effect on

an orifice plate. Their results are very interesting in showing that even though the

profile from the tube bundle at about 20D was very close to the fully developed

turbulent profile, approximating to Equation (2.4) with n = 7

the turbulence

intensity pattern is markedly different, suggesting that this is a factor in the re-

sponse of orifice plates. They showed that the orifice coefficient downstream of the

elbow and the tube bundle, compared with the correct value, was high by about

0.2% between 10D and 15D and fell to about

0.1%

high by about 20D. There was a

point closer to the orifice plate where the coefficients were approximately the same,

but it would be unwise to rely on this for precise measurements (cf. Morrow et al.

1991 who used an arrangement that allowed them to slide a tube bundle condi-

tioner along the pipe between a 90° long-radius bend and an orifice plate to obtain

the variation of discharge coefficient with position for a gas flow. Overall the re-

sults appeared to suggest that, if possible, the conditioner should be next to the

bend.)

Sattary (1991) concluded from the EEC orifice plate program on installation

effects that the ISO 5167 and AGA Report No 3 minimum straight length specifica-

tions needed to be revised. The results for conditioners 19D upstream of an orifice

in fully developed flows showed shifts of up to 0.33-0.5% for p = 0.57, rising to

about 0.57-0.75% for p = 0.75. For a p = 0.2, there was negligible effect from a

tube-bundle conditioner at 5D. The reader concerned with this topic is encouraged

to refer to the original paper, which has extensive experimental data and indications

that there is variation between the performances of the various straighteners. There

is some discrepancy between the various standards. For two bends in perpendicular

planes, by far the most serious disturbance, the ISO requirement for no loss in ac-

curacy is that the orifice should be at least 44D downstream for a p = 0.55 and 70D

for a p = 0.75. On the other hand, the blanket requirement for a flow straightener

is that there should be at least 20D from the fitting to the straightener and at least

22D from the straightener to the meter. This is a total of at least 42D plus the length

of the straightener, and greater than or equal to all other requirements for p up to

0.75,

apart from those for two or more bends in different planes. The equivalent

values for AGA for two bends or tees not in the same plane are (Sattary 1991) for

P =

0.57, 23.5D, and for p

0.75, 35.5D, and with a short tube bundle straightener

for the general case is 17D (straightener distance 5.5D + installation distance 11.5D).

Sattary's results appeared to suggest that the values without straightener were not

conclusive for ISO, but, apart from the two bends in perpendicular planes, the AGA

lengths may be too short.

106 ORIFICE PLATE METERS

Orifice Plates

•I Direction of flow

_ JL JL _JL _J

Figure 5.6. Other orifices (reproduced with permission of

Elsag

Bailey-Bush Beach Engineering

Division).

5.5 OTHER ORIFICE PLATES

Figure 5.6 gives a range of orifices that are useful for special purposes, data for some

of which may be obtained from

1042 Section 1.2: 1989.

The

quarter circle (quadrant) orifi

ceplate is for low Reynolds number flows, which

result from high viscosity liquids. The entry is more difficult to make precisely

than that of the square-edged orifice, and manufacturing tolerances are there-

fore critical. An expression for the discharge coefficient in the standard has an

uncertainty in the region of 2-2.5%.

The

conical entrance

design is for very low Reynolds number flows, which result

from very high viscosity liquids. The entry is again more difficult to make

precisely than that of the square-edged orifice, and manufacturing tolerances

are therefore critical. Provided that the standard is followed, C = 0.734 with

uncertainty of 2%.

Eccentric

and

chordal (segmental) orifices

are more suitable for flows that have a

second component in them. Of these, the eccentric orifice plate is preferred,

presumably on grounds of more accurate manufacture and more flexible sizing

and of being defined in the standard. Thus for a liquid with solid matter, one

would choose an eccentric orifice with the hole at the bottom of the pipe,

whereas for a liquid with gas entrained, an orifice at the top of the pipe would

be chosen. For p in the range 0.46-0.84, the standard gives the coefficient in

the range 0.597-0.629 with an uncertainty in the region of 1-2%. In cases

where the position of the second component is not clear, it may be necessary

to go to a chordal orifice with the edge vertical to allow the second component

to pass wherever it is in the pipe.

Ball

orifices

(see Chapter 8).

Slotted orifices

(see Chapter 8).

5.6 DEFLECTION OF ORIFICE PLATE AT HIGH PRESSURE

Jepson and Chipchase (1975) provided a formula to calculate the deflection in the

downstream direction and consequent error for plates operating at high pressure.