Барыкин С.Г., Плотникова Н.В. Системы искусственного интеллекта

Подождите немного. Документ загружается.

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Южно-Уральский государственный университет

Кафедра “Системы управления”

007(07)

Б269

С.Г. Барыкин, Н.В. Плотникова

СИСТЕМЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА

Конспект лекций

Челябинск

Издательство ЮУрГУ

2004

УДК 007(07)

Барыкин С.Г., Плотникова Н.В. Системы искусственного интеллекта:

Конспект лекций. – Челябинск: Изд. ЮУрГУ, 2004. – 85 с.

В пособии рассмотрены теоретические и практические вопросы построения

различных систем с элементами искусственного интеллекта; приведены

логические модели и фреймы для представления знаний, примеры построения

систем искусственного интеллекта; рассмотрены вопросы распознавания образов,

приведены алгоритмы обработки изображений в системах технического зрения и

моделях восприятия речи. Материал иллюстрирован описанием конкретных

систем искусственного интеллекта.

Пособие предназначено для студентов специальности 220200 –

«Автоматизированные системы обработки информации и управления», дневного

и заочного отделений, магистерских программ образовательных направлений

553000, 550200, а также может быть полезно студентам других специальностей,

изучающим курс систем искусственного интеллекта.

Ил. 42, табл. 6. список лит. – 15 назв.

Рецензенты: Б.Л. Маринин, Ю.Б. Курочкин.

 Издательство ЮУрГУ, 2004.

ВВЕДЕНИЕ

В последние годы в нашей стране и за рубежом существенно повысился

интерес к исследованию прикладных интеллектуальных управляющих систем, их

разработке и внедрению в промышленную и непромышленную сферы.

Первые результаты появились благодаря исследованиям, связанным с соз-

данием машинных программ, имитирующих творческую деятельность человека.

Они разрабатывались в рамках научного направления, получившего в дальней-

шем название «искусственный интеллект».

Впервые понятие «интеллектуальная машина» или «интеллектуальная сис-

тема» возникло по меньшей мере два десятка лет тому назад [3].

Интеллектуальные системы в последнее время стали весьма распростра-

ненным коммерческим продуктом, находящим широкий спрос пользователей-

специалистов в самых разнообразных областях инженерно-технической и науч-

но-технической сфер деятельности. Концептуальная архитектура любой интел-

лектуальной (в частности, экспертной) системы общеизвестна и содержит сле-

дующие основные блоки:

– база знаний с развитыми механизмами вывода на знаниях;

– интеллектуальный решатель (формулирующий постановку и общий план ре-

шения задачи);

– интеллектуальный планировщик (формирующий конкретный план решения

задачи);

– система объяснения;

– интерфейс с пользователем.

Интеллектуальные системы могут существенным образом различаться по

архитектуре и выполняемым функциями, но в них всегда в той или иной мере

присутствуют указанные блоки. Для реализации интеллектуальной системы не-

обходимо предусмотреть следующие слои обработки неопределенной информа-

ции (слои интеллектуальности):

– слой прогноза событий

– слой самообучения и адаптации;

– слой работы с базами событий, знаний и формирования решений;

– исполнительный слой.

Каждый из перечисленных слоев имеет свою функциональную специфику

и в реальной системе может состоять из нескольких уровней. При этом в самом

нижнем исполнительном слое могут использоваться классические модели систем

автоматического управления. Все остальные слои более высокого ранга можно

рассматривать как надстройку над традиционными классическими моделями, от-

вечающую требованиям современной информационной технологии работы со

знаниями и существенно расширяющую возможности этих моделей.

В зависимости от того, сколько слоев интеллектуальности имеет та или

иная система, можно говорить о разных степенях ее интеллектуальности.

Интеллектуальные системы – это системы, строящиеся с применением но-

вой информационной технологии обработки и использования знаний.

ГЛАВА 1. ПРЕДСТАВЛЕНИЕ ЗНАНИЙ

Термин «знание» в работах по искусственному интеллекту так же значите-

лен, как термин «данные» в области программирования. Переход от данных к

знаниям – логическое следствие развития и усложнения информационных струк-

тур, обрабатываемых на ЭВМ.

1.1.

ЛОГИЧЕСКИЕ МОДЕЛИ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ

Для описания внешнего мира и поиска решений в искусственном интел-

лекте широко используется язык и аппарат исчисления предикатов [8].

Исчисление предикатов

Для автоматизации процессов постановки и решения интеллектуальных за-

дач необходим адекватный язык. Этот язык должен служить не только и не

столько средством представления знаний (информации), сколько средством ло-

гического анализа интеллектуальных задач.

Обычные человеческие языки, развивавшиеся под влиянием практических

потребностей простоты общения (что далеко не всегда совместимо с точностью

и надёжностью логического анализа), для этой цели плохо подходят. По этой

причине практически необходимо использовать в качестве языка специально

созданный формализованный язык. Такой язык в противоположность обычному

языку должен следовать за логической формой и воспроизводить её даже в

ущерб краткости и лёгкости общения, если это будет необходимо. Главной отли-

чительной чертой такого формализованного языка является наличие в нём осо-

бой системы логического вывода или дедукции.

Логическая функция P(x

, …, x

), принимающая одно из значений «истина»

или «ложь», аргументы которой пробегают значения из произвольного множест-

ва M, называется предикатом Р в предметной области М. Аргументы x

, …, x

называются предметными переменным, а их конкретные значения называют

предметными постоянными. Предметные переменные и предметные постоянные

образуют класс логических понятий, называемых термами. В сущности, преди-

кат определяет некоторое отношение относительно объектов из М. При замеще-

нии аргумента

(предметной переменной) некоторым его значением а (пред-

метной постоянной) n-местный предикат P(x

, …, x

) превращается в (n–1)-

местный предикат и от x

он не зависит. Замена всех переменных предметными

постоянными дает 0-местный предикат или обычное высказывание.

Утверждение, что все x∈ M обладают свойством P(x), записывают с помо-

щью квантора общности ∀ x в виде ∀x P(x), а утверждение, что существует хотя

бы один объект x из М, обладающий свойством P(x), записывают с помощью

квантора существования ∃ x в виде ∃ x P(x). Предикат уже не зависит от пере-

менной, связанной квантором.

Выражения, которые можно образовывать применением к предикатам

кванторов и сентенциональных связок (¬ – отрицание, ∧ – конъюнкция, ∨ –

дизъюнкция, →– импликация, ∼ – эквивалентность), представляют собой форму-

лы логики предикатов. Всякая формула без свободных переменных (замкнутая

формула) представляет собой высказывание, которое или истинно, или ложно, а

всякая формула со свободными переменными задает некоторое отношение в

предметной области. Это отношение может быть истинным или ложным в зави-

симости от приписываемых значений свободных переменных. Для установления

значения формулы необходимо сначала определить значения входящих в данную

формулу предикатов при замещении свободных переменных элементами из

предметного множества. Затем последовательно используются общие свойства

сентенциональных связок и кванторов.

Перевод предложений с русского языка на язык логики предикатов при не-

которых навыках не вызывает затруднений. Пусть, например, предикат S(x) оп-

ределяет свойство x быть роботом, т.е. S(x) = «x – робот», а другой предикат

P(x)= «x – манипулятор». Тогда четыре категорических высказывания: а) «всякий

робот есть манипулятор»; б) «никакой робот не является манипулятором»; в)

«некоторые роботы являются манипуляторами»; г) «некоторые роботы не явля-

ются манипуляторами» можно представить символически па языке логики пре-

дикатов:

а)

));()(( xPxSx →∀

б)

));()(( xPxSx ¬→∀

в)

));()(( xPxSx

∧

∃

г)

)).()(( xPxSx ¬

∧

∃

Особый интерес в логике предикатов представляют общезначимые форму-

лы, которые истинны при любом значении входящих в них свободных перемен-

ных и предикатов. Исходя из понятия общезначимости, можно дать следующее

определение логического следствия: формула В логически следует (выводится)

из системы формул (посылок) A: {A

, A

, …, A

}, если формула А →В является

общезначимой. Отметим, что если В логически следует из А, то формула А

∧

может принимать только ложные значения. Этот факт выражают также иначе.

Говорят, что множество формул {A

U В} в этом случае является противоречием

(несовместно, неудовлетворимо). Справедливо и обратное утверждение: из не-

удовлетворимости множества формул {A

U В} вытекает логическое следование

В из А.

Язык предикатов широко используется при управлении роботами [9]. Мо-

дель среды робота представляется совокупностью формул исчисления предика-

тов, которым придано «содержание»: формулы интерпретируются как некоторые

утверждения, касающиеся рассматриваемой области. При данной интерпретации

всегда можно вычислить значение любой формулы.

Каждое действие робота может изменить модель среды. Вместе с тем робот

может выполнить только такое действие, которое допустимо для данной модели.

Например, робот не может вставить болт в отверстие, если этот болт не взят

схватом и не ориентирован подходящим образом.

Всевозможные действия робота определяются множеством операторов.

Оператор входит в это множество, если существует хотя бы одна модель среды, в

которой этот оператор может быть применен. Необходимо точно определить эф-

фект действия каждого оператора. Условия применимости оператора, формули-

руемые на языке логики предикатов, позволяют установить, можно ли применить

этот оператор в данной модели. Если его можно применить, то необходимо ука-

зать, как трансформируется модель среды после применения оператора.

Пусть М – модель среды, а В – условие применимости некоторого операто-

ра. Неудовлетворимость множества формул {М

U В} означает, что этот опера-

тор может быть применен. Часто оператор может зависеть от параметра, т. е.

)( pBB =

. В этом случае для применимости оператора достаточно найти хотя бы

одно значение параметра p

′

, для которого {

)( pBM

′

} является проти-

воречием.

Кроме этого, логическое следование некоторого утверждения из множества

посылок (аксиом) необходимо доказывать и при проверке достижимости цели

управления в данной модели. Пусть B – цель управления, сформулированная па

языке логики предикатов, а М – модель среды, построенная в результате некото-

рых предшествующих действий. Если В логически следует из М, т. е. {М

U В}

является противоречием, то цель управления достигнута. В противном случае

надо искать операторы, применимые в данной модели, с целью дальнейших пре-

образований.

Для построения машинных программ, автоматически доказывающих логи-

ческие следования некоторых утверждений на основе заданного набора посылок,

составляющих содержание модели, можно пользоваться различными правилами

вывода, разработанными в математической логике. Наиболее перспективным

правилом вывода в настоящее время признан метод резолюций (или иначе – ме-

тод резольвенций [11]) Дж. А. Робинсона (1965), который дает наиболее механи-

зируемый алгоритм доказательства. Его преимущество состоит в проверке ми-

нимального числа частных случаев при поиске противоречия.

Рассмотрим простой пример планирования действий манипуляционного

робота, с помощью которого можно проиллюстрировать применение аппарата

логики предикатов. Этот пример представляет такую перефразировку известной

задачи об обезьяне и бананах [9], которая в достаточной степени соответствует

задачам манипуляционных роботов. Кроме этого, в нашем примере, так же как и

в известной системе STRIPS [8], процесс логического доказательства теорем бу-

дет полностью отделен от процесса поиска в пространстве моделей среды (в от-

личие от других систем, в которых для отыскания нужной последовательности

операторов используются исключительно лишь формальные методы логики). В

нашем случае метод доказательства теорем используется только внутри некото-

рой заданной модели среды для ответов на вопросы, касающиеся применимости

различных операторов и достижимости цели. Это позволяет проиллюстрировать

сразу два аспекта рассматриваемого здесь эвристического направления искусст-

венного интеллекта: поиск в пространстве состояний и применение формальной

логики.

Пусть роботу-манипулятору дано задание навинтить гайку на болт. Поло-

жение болта задано вектором параметров с, а гайки – вектором b. Схват манипу-

лятора в начальный момент времени находится в положении а. Следовательно,

описание начальной модели среды содержит пять предикатов





















),схват(

),гайка(

aAT

bAT

SCREWED

INHAND

ONBOLT

Предикат ONBOLT имеет значение «истинно» только тогда, когда гайка

надета на болт, предикат INHAND имеет значение «истинно» только тогда, когда

гайка зажата между губками схвата, а предикат SCREWED имеет истинное зна-

чение, когда выполнено завинчивание.

В распоряжении манипулятора имеются пять операторов (элементарных

движений): «подойти» (u), «переместить» (v), «взять», «надеть», «завинтить».

Первый оператор – «подойти» (u) – выполняет перемещение в точку u только

схвата (без гайки), второй оператор – «переместить» (v) – выполняет перенос

гайки, взятой схватом в точку v. Смысл других операторов понятен, причем для

сокращения дерева поиска мы не учитываем возможность применения таких со-

ответственно противоположных по смыслу операторов, как «отпустить»,

«снять», «отвинтить».

Цель управления – получить такую модель средь из которой логически вы-

текает утверждение SCREWED.

Сначала опишем условия применимости операторов, а также модели сре-

ды, которые возникают после применения каждого оператора. Эти описания для

наших пяти операторов можно представить следующим образом:

1. Оператор «подойти» (u).

Условие применимости:

INHAND.

Результирующая модель среды отличается от модели предшествующей

указанному действию, лишь тем, что вместо предиката AT (схват,

∗ ), где

∗

– лю-

бой терм, появляется предикат AT (схват, u).

2. Оператор «переместить» (v).

Условие применимости:

)).,схват(),гайка()(( x

NHANDONBOL

∧

∃

∧

∧¬

Результирующее состояние содержит предикаты





















),схват(

),гайка(

vAT

SCREWED

INHAND

ONBOLT

3. Оператор «взять».

Условие применимости:

)).,схват(),гайк

()((

INHAND ∧

∃

∧

Результирующая модель получается из предшествующей модели путем

снятия знака отрицания у предиката

INHAND.

4. Оператор «надеть».

Условие применимости:

),схват(),гайк

( c

INHAND

∧

.Результирующая модель среды по-

лучается из предшествующей путем снятия знака отрицания у предиката

.INHAND¬

5. Оператор «навинтить».

Условие применимости:

),схват(),гайк

( c

NHANDONBOL

∧

. В

результате применимости этого оператора будет снят знак отрицания у предика-

та

¬ SCREWED.

Теперь перейдем к поиску последовательности операторов, обеспечиваю-

щих выполнение заданной технологической операции. Получить целевую модель

среды можно с помощью метода проб и ошибок, применяя возможные операто-

ры к начальной

И последующим моделям и всякий раз пытаясь доказать, что ут-

верждение SCREWED логически следует из утверждений, порожденных послед-

ним применением некоторого оператора. Так как очевидно, что модель среды M

дополненная отрицанием целевого предложения, не содержит противоречия, мы

заключаем, что цель в исходной модели не достигнута. Затем методом простей-

шего перебора определяем, какой из операторов применим. С этой целью можно

искать доказательство того, что условие применимости оператора следует из M

Человек сразу определил бы, что в модели M

можно применить только оператор

подойти (u), но машинная программа будет аккуратно проверять условия приме-

нимости каждого оператора. Например, для оператора «надеть» программа сна-

чала составит отрицание условия применимости

),схват(),гайка( c

INHAND

∨

и попробует доказать, что это предложение вместе с M

образует противоречие.

Но это ей не удастся. Поэтому будет сделан вывод, что данный оператор непри-

меним. Аналогичным образом машинная программа установит, что непримени-

мы в M

операторы «переместить» (v), «взять», «навинтить», но применим опера-

тор «подойти» (u), поскольку множество формул { M

U INHAND} неудовлетво-

римо.

В результате применения оператора «подойти» (u) возникает новая модель

среды с параметром u:





















),схват(

),гайка(

)(

uAT

bAT

SCREWED

INHAND

ONBOLT

Как только появляется новая модель среды, необходимо выяснить, сущест-

вует ли по крайней мере частный случай модели, из которой следует целевое ут-

верждение. В данном случае ни при каком значении u из M

(u) целевая модель

логически не следует.

Далее находим операторы, которые можно применить в модели M

(u). По-

прежнему можно применить оператор «подойти»

(u), но он оставляет модель M

без изменений. Подстановка в M

вместо u величины b дает частный случай этой

модели, в которой можно применить оператор «переместить» (v). Обозначим

этот частный случай через M

(b). В этом частном случае применимы операторы

«подойти» (u), который снова дает старую модель, и «взять».

Второй оператор порождает модель





















),схват(

),гайка(

bAT

SCREWED

INHAND

ONBOLT

Опять методом простого перебора устанавливаем, что оператор «перемес-

тить» (v) дает новую модель





















),схват(

),гайка(

)(

vAT

SCREWED

INHAND

ONBOLT

причем предшествующая модель является частным случаем полученной модели

(b).

Однако гораздо интереснее другой частный случай – M

(c). В этой модели

условие применимости оператора «надеть» уже является логическим следствием.

Применение этого оператора снимает знак отрицания у предиката

¬ ONBOLT и

тем самым обеспечивает условие применимости оператора «навинтить». В по-

«Подойти»

(

)

» «Надеть» «Навинтить»

(

)

(

)

Подстановка u = b Подстановка v = c

«Взять» «Пе

еместить»

(

)

следних моделях допустимы и некоторые другие операторы, но они возвращают

процесс поиска к уже пройденным моделям.

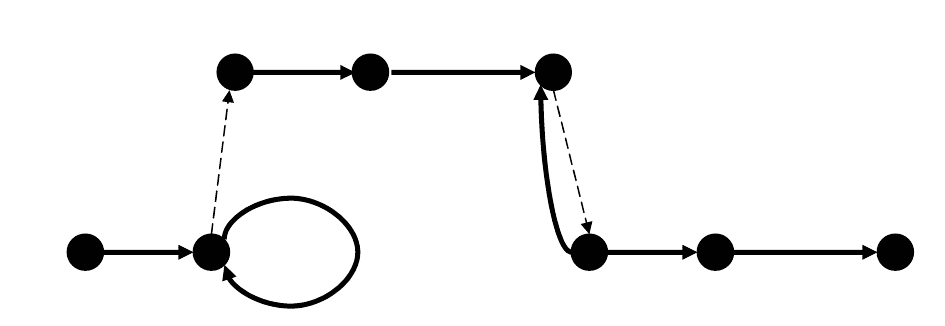
Весь процесс поиска целевой модели наглядно представлен на рис. 1.1. как

процесс поиска дуги на графе, каждая вершина которого представляет собой не-

которое состояние (модель), а каждая дуга характеризует действие, допустимое в

том состоянии, из которого эта дуга выходит.

Рис. 1.1. Граф действий и состояний при автоматическом планировании

операции «навинчивание гайки на болт»

Таким образом, логически доказывая условия применимости операторов,

исходя из множества утверждений текущей модели, находим допустимые опера-

торы и частные случаи модели, которые порождают новые допустимые действия

и новые модели. Построив целевую модель, с помощью обратного хода на графе

извлекаем план выполнения заданной технологической операции. В данном слу-

чае этот план реализуется последовательностью операторов: «подойти» (b);

«взять» «переместить» (с); «надеть»; «навинтить». Каждое элементарное движе-

ние этой синтезированной последовательности может быть реализовано на так-

тическом уровне системы управления в рамках кинематических алгоритмов.

Рассмотренный пример очень прост. С его помощью показано, что на стра-

тегическом уровне системы управления с помощью эвристического поиска мо-

жет быть хотя бы в принципе синтезирована последовательность действий, исхо-

дя из технологического задания. В задачах, имеющих практическую важность,

число вершин выстраиваемого графа, как правило, очень велико, а доказательст-

во теорем в сложной модели среды может потребовать значительной оператив-

ной памяти ЦВМ нереального машинного времени.

Кроме этого, адекватное внутреннее представление «рабочего мира» робо-

та во всем его многообразии – далеко не решенная задача. Аппарат логики пре-

дикатов предлагает здесь лишь некоторые возможности. Предложенные в на-

стоящее время решения двух основных проблем искусственного интеллекта:

проблемы эвристик и проблемы представления среды следует рассматривать как

только первые приближения).

(b) М

(v)