Барыкин С.Г., Плотникова Н.В. Системы искусственного интеллекта

Подождите немного. Документ загружается.

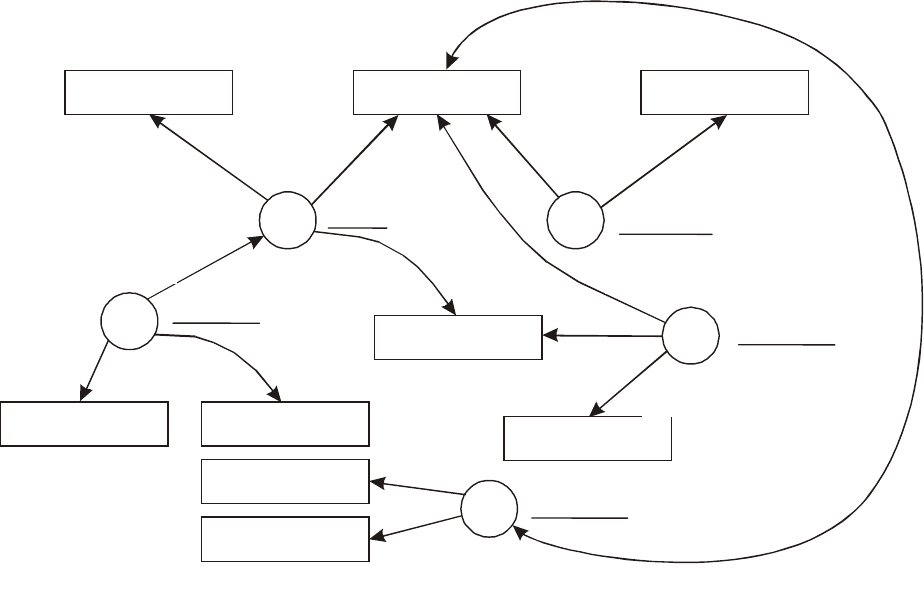
Рис. 1.9. Семантическая сеть

Важным понятием в семантических сетях является десигнат – уникальное

внутрисистемное имя, которое ставится в соответствие некоторому объекту

предметной области, если о нем в данный момент времени нет полной информа-

ции. Десигнат отражает наиболее значимый смысл объекта, в частности просто

факт его существования. Например, фраза типа «Станок С1 имеет накопитель»

содержит неопределенность относительно характеристик накопителя. Предпо-

ложим, что по мере поступления информации (это может происходить в процес-

се проектирования) будут уточнены емкости накопителя, его габариты и т. д. То-

гда указанную фразу можно представить следующим образом:

(F1: ИМЕЕТ агент СТАНОК объект D1)

(D1: имя НАКОПИТЕЛЬ)

(D1: габарит _________ )

(D1: емкость _________ ) .

Здесь F1 – метка факта; D1 – метка десигната. Пустые места заполняются в

процессе накопления данных значениями соответствующего атрибута. Таким об-

разом, в момент первого упоминания об объекте в базе данных заводится его де-

сигнат, которым можно манипулировать, не ожидая полной информации об объекте.

Введение десигнатов увеличивает гибкость семантической сети, однако их использо-

вание требует дополнительных вычислительных ресурсов.

Рассмотрим некоторые вопросы построения интеллектуальных банков

данных на основе семантических сетей. Основным принципом их организации

является разделение экстенсиональных и интенсиональных знаний, при этом

экстенсиональная семантическая сеть является основой базы данных, а интен-

агент

место

объект

агент

Робот

Кассета

Деталь

F2 F4

Обработка

Станок

Штабелер

Ячейка

Робокар

Склад

объект

закончил

содержит

перевозит

помещает

грузит

условие

«если»

агент

объект

агент

ад

есат

ад

есат

сиональная – базы знаний. Такое «расслоение» системы представления знаний

(СПЗ) существенно повышает ее выразительные возможности по сравнению, на-

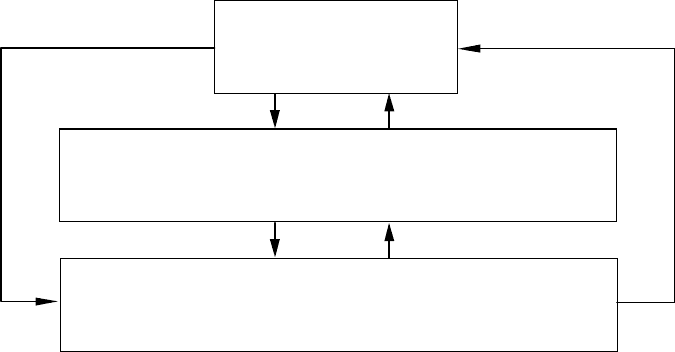
пример, с логическими моделями. Структура системы представления знаний та-

кого типа изображена на рис. 1.10. Условность этого изображения связана, в ча-

стности, с отсутствием строгого разделения указанных компонент СПЗ при их

реализации.

Система

управления

базой знаний

База знаний

Интенсиональная семантическая сеть

База данных

Экстенсиональная семантическая сеть

Рис. 1.10. Структура системы представления знаний

При функционировании СПЗ основным является информационно–

поисковый режим. Запрос представляет собой набор фактов (ситуацию), при

описании которых допускается использование переменных в позициях значений

атрибутов, атрибутов и имен отношений. Запрос можно представить графом, в

котором вершины, соответствующие некоторым переменным, не определены.

Поиск ответа заключается в решении задачи изоморфного вложения графа за-

проса (или его подграфа) в семантическую сеть. Можно выделить два основных

типа запросов – на существование и на перечисление. Запрос на существование

не содержит переменных и предусматривает ответ типа ДА, если изоморфное

вложение графа в семантическую сеть удалось, и НЕТ – в противном случае. При

обработке перечисляющего запроса происходит поиск (перечисление) всех воз-

можных изоморфных графу запроса подграфов в семантической сети, а также

конкретизация переменных.

Пусть, например, имеется запрос «Оператор сообщил, что робокар что-то

перевозит. Определить, что и куда перевозит робокар». Поиск ответа осуществ-

ляется в семантической сети, изображенной на рис. 1.9. Запрос можно предста-

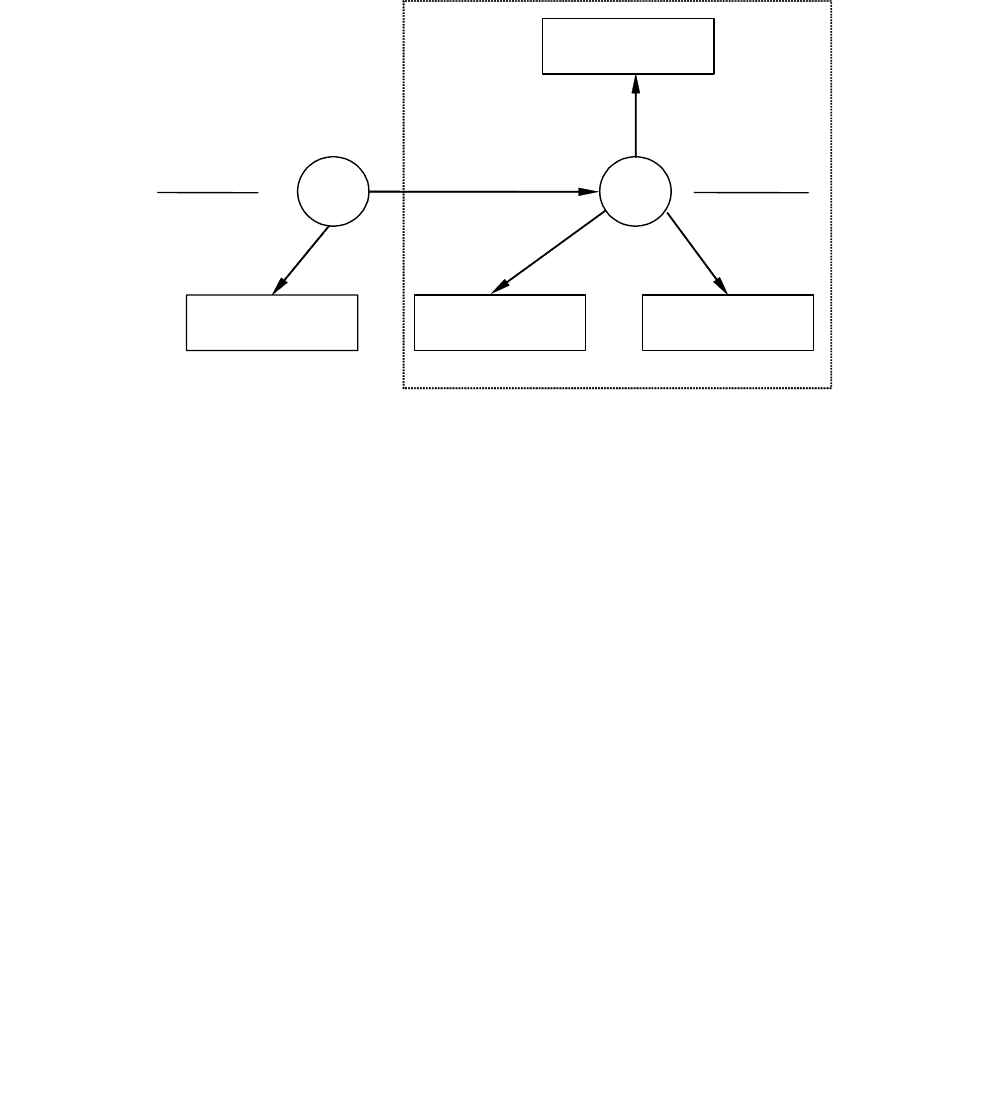
вить графом (рис. 1.11), в котором вершины X и Y требуют конкретизации, а F6

является фактом сообщения. Очевидно, звездообразный подграф факта F в графе

запроса (на рисунке выделен штриховой линией) может быть изоморфно вложен

в семантическую сеть при совмещении с F3 на рис. 1.9.

Y РОБОКАР ОПЕРАТОР

F F6

объект

что

пе

евозит сооб

ил

др

есат

агент

Рис. 1.11. Граф запроса

При этом будут конкретизированы вершины X и Y: X – КАССЕТА, Y –

СКЛАД. Ответ будет выглядеть так: РОБОКАР ПЕРЕВОЗИТ КАССЕТУ НА

СКЛАД. Этот пример иллюстрирует поиск ответа в семантической сети в упро-

щенной форме, так как здесь не рассматривается процесс интерпретации запроса,

который первоначально выражается на специальном языке общения.

Семантическая сеть может использоваться для представления как деклара-

тивных, так и процедуральных знаний. Представление декларативных знаний

использует так называемые базовые отношения, характеризующиеся тем, что их

экстенсионал полностью хранится в базе данных. Процедуральные знания связа-

ны виртуальными отношениями, которые не имеют экстенсионала, хранимого в

явной форме. В описании этих отношений содержатся правила (программы), по-

зволяющие конструировать факты по мере необходимости. Виртуальные отно-

шения реализуются в виде вычислимых отношений, имеющих функциональный

или предикатный характер, либо в виде правил, использующих свойства симмет-

ричности, рефлексивности или транзитивности (в тех случаях, когда они имеют

место в моделируемой предметной области).

ГЛАВА 2. СИСТЕМЫ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА

2.1. Игровые системы

В современной математике слово граф имеет особое значение. Граф со-

стоит из вершин, соединённых между собой рёбрами: каждой вершине при-

писывается определённый смысл. Каждое ребро указывает на определённое от-

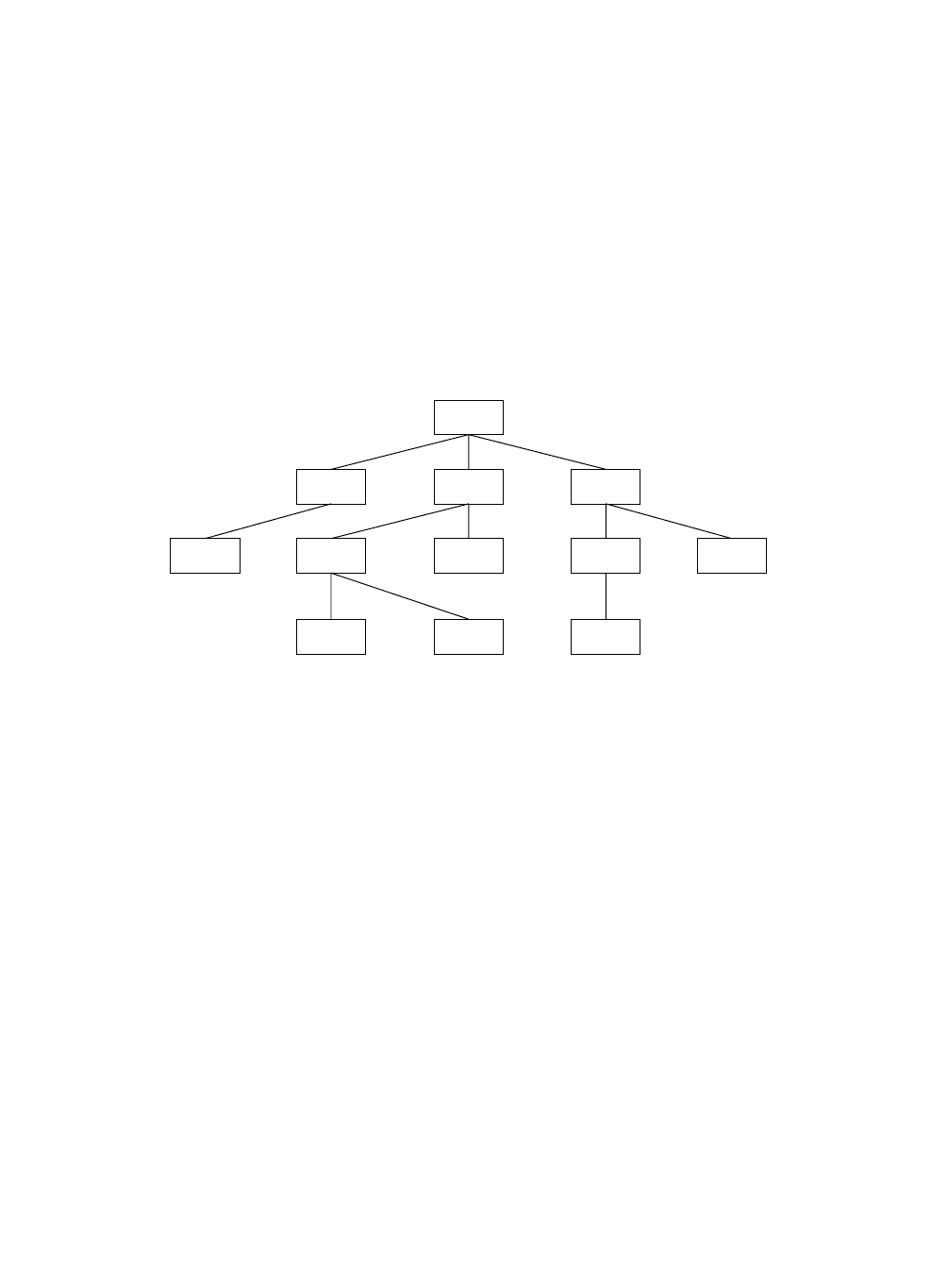
ношение между парой соединяемых их вершин [6]. На рис. 2.1. показано дерево,

вершины которого изображены прямоугольниками. Деревья, представляющие

системы обработки данных, в отличие от реальных деревьев обычно изображают

корнем вверх.

Рис. 2.1. Древовидная структура

На рёбрах графа, показанного на рис. 2.1, нет стрелок, хотя по смыслу они

асимметричны, – общее расположение показывает, как соединены вершины.

В проблеме искусственного интеллекта деревья представляют особый ин-

терес; тому имеется несколько причин. Одна из них заключается в том, что лю-

бой дискретный процесс принятия решений в заданной детерминированной сис-

теме может быть представлен в виде дерева. Если корень дерева соответствует

начальному состоянию системы, то его дочерние вершины соответствуют со-

стояниям, которые могут быть результатом применения различных операций из

числа имеющихся. Далее, для каждой из таких дочерних вершин существует не-

которое множество возможных операций, каждая из которых приводит к новому

состоянию, представляемому внучатыми вершинами, и т.д.

Игра в шахматы и другие игры с помощью вычислительных машин – про-

блемы, которым в работах по искусственному интеллекту уделяется большое

внимание. В программах, оказавшихся успешными для ведения целого ряда игр,

явным образом обследуется дерево, которое указывает возможные продолжения

игры из заданной начальной ситуации.

Древняя игра в шахматы бросает несомненный вызов учёным, работающим

в области искусственного интеллекта. Были попытки ещё до появления ЭВМ по-

строить автоматы для игры в шахматы. Но в лучшем случае это были системы с

ограниченным числом фигур.

С появлением вычислительных машин возникла возможность создания на-

стоящего автомата для игры в шахматы. Принцип работы точного автомата опи-

рается на исследование дерева возможных продолжений игры (дерево просмотра

возможностей).

Корневая вершина такого дерева представляет текущую конфигурацию

фигур на шахматной доске, а программа производит выбор хода. В середине

шахматной партии у игрока обычно имеется около тридцати возможных вари-

антов следующего хода. Возникающие в результате их перебора вершины могут

быть представлены как дочерние для данной корневой вершины.

В каждой из дочерних вершин возможно около тридцати ответов против-

ника, так что для изображения результирующих конфигураций потребуется ещё

около 900 вершин и т.д., дерево быстро «разрастается». Существуют два типа

вершин. Одни, наподобие корневой вершины, представляют конфигурации, в ко-

торых ход за программой; они называются альфа-вершинами. Вершины другого

типа, представляющие конфигурации, в которых ход за противником, называют-

ся бета-вершинами. Последующие уровни такого дерева возможностей заняты по

очереди альфа- и бета-вершинами.

Если бы дерево можно было обследовать полностью, т.е. вплоть до всех

листьев, представляющих все возможные окончания в данной игре, то имелась

бы возможность выбрать ход, обеспечивающий для машины выигрыш независи-

мо от реакций противника. В действительности же полный просмотр всего дере-

ва не возможен. Установлено [15], что для обследования всего дерева в середине

шахматной игры потребуется 10

лет машинного времени – в предположении

весьма быстродействующей машины. Если быстродействие такой машины уве-

личить ещё в миллион раз, то и при этом потребовалось бы 10

лет – тоже слиш-

ком много. Эффект комбинаторного взрыва проявился бы здесь со всей силой,

так что о полном просмотре дерева не может быть и речи. Вместо полного про-

смотра дерева в программах игры в шахматы обследуется лишь небольшая его

часть. В таком случае говорят, что дерево подвергается подрезке. Простейший

метод подрезки – обрыв дерева на определённой глубине, т.е. просмотр вперед

на некоторое фиксированное число полуходов (полуход – это ход одного из иг-

роков). Нельзя сказать, что это хороший метод игры, но даже при использовании

других методов допустимую глубину ограничивают. (Под «хорошей» подрезкой

понимается метод, обеспечивающий высокое качество игры при данном объёме

вычислительных затрат).

Тот факт, что просматривается только часть дерева, означает, что процесс

обследования должен заканчиваться в вершинах, которые не являются листьями.

Это терминальные вершины, или листья, обследуемого поддерева, но не полного

дерева. Методы, используемые в программах, основаны на числовой оценке для

каждой такой вершины относительной силы обоих игроков в момент достижения

данной конфигурации. Эта оценка принимается равной нулю, когда силы парт-

неров равны, она положительна, когда машина, по-видимому, имеет преимуще-

ство, и отрицательна, когда противник машины оказывается сильнее. Эту чис-

ленную оценку называют оценивающим полиномом (так как обычно она имеет

полиномиальный вид, или, проще говоря, вид взвешенной суммы), или статисти-

ческой оценочной функцией (с.о.ф.).

Важной компонентой любой статистической оценивающей функции явля-

ется материальное соотношение, или перевес фигур. Этот член просто соот-

ветствует сравнению фигур, имеющихся у игроков, причем каждой фигуре при-

дается определенное значение ценности. Самое высокое значение ценности име-

ет ферзь, затем (как существенно менее ценные) следуют в порядке убывания

ценности конь, слон и ладья, а наименее ценной из всех фигур является пешка.

Второй важной компонентой оценочной функции, вероятнее всего должна

быть некая мера относительной подвижности фигур, причем более сильным счи-

тается тот игрок, у которого подвижность фигур больше. Простым критерием

подвижности является число допустимых ходов, имеющихся у игрока. Можно

также дать численную оценку контроля центра и других критериев, знакомых

игрокам в шахматы.

После того как произведена оценка каждой терминальной вершины об-

следуемого поддерева, следующий шаг состоит в перенесении результатов этих

оценок вверх по дереву («вверх» означает в направлении корня дерева). Метод,

которым это достигается, называется минимаксным; он заключается в следую-

щем. Для альфа-вершин (представляющих позиции, в которых ход делает маши-

на) принимается значение, равное наибольшему значению из указанных для до-

черних вершин. Это абсолютно оправданно, поскольку в таком случае машина

сделает наиболее выгодный для себя ход. Однако для бета-вершин принимается

наименьшее из значений оценки для дочерних вершин, поскольку можно пред-

положить, что противник сделает ход, наименее выгодный машине.

В конечном итоге некоторое оценочное значение приписывается корневой

вершине. Поскольку она является альфа-вершиной, это значение будет наи-

большим среди значений дочерних вершин. Ход, который выбирает машина,

преобразует существующую на шахматной доске конфигурацию, представ-

ленную корневой вершиной, в конфигурацию, представленную той дочерней

вершиной, из которой было взято значение оценки для корневой вершины. Рас-

сматриваемая задача, безусловно, является плохо определенной, поскольку не-

возможен просмотр всего дерева. И даже если бы полный исчерпывающий про-

смотр всего дерева был возможен, эта процедура не обязательно указывала бы

совершенный ход, обеспечивающий победу. Тот ход, который человек-

шахматист рассматривал бы как наилучший, по-видимому, зависел бы от игро-

вых возможностей и других характеристик противника. Любой выбор, учиты-

вающий подобные обстоятельства, несомненно, представляет собой решение

плохо определенной задачи. Описанный же выше машинный метод ни в коей

мере не учитывает характеристики партнера по игре. Действие рассмотренного

нами метода было бы очень простым, если бы дерево отсекалось столь сильно,

что остались бы только корневая вершина и ее дочерние вершины. Тогда стати-

стическая оценочная функция (с.о.ф.) применялась бы к каждой дочерней вер-

шине, и та, что соответствовала бы наибольшему значению функции, определяла

бы следующий ход. Было обнаружено, что у программы, работающей таким об-

разом, очень легко выиграть. Пока еще не удалось найти форму с.о.ф., которая

могла бы быть достаточно эффективной. Чем на большее число шагов происхо-

дит просмотр вперед, тем лучше игра и тем в меньшей степени качество игры за-

висит от точного вида с.о.ф.

Шахматы отнюдь не единственная игра, которой уделялось внимание при

работе над проблемой искусственного интеллекта. Предметом исследования ста-

ли многие малоизвестные и известные игры, такие, например, как шашки.

Среди работ, посвященных моделированию с помощью ЭВМ игр, отлич-

ных от шахмат, наиболее известна программа Сэмюеля [15] для игры в шашки

для доски 8x8. Эта игра значительно проще шахмат Согласно оценкам, число

возможных игровых ситуаций в шашках равно кубическому корню из числа воз-

можных ситуаций в шахматах.

В общих чертах метод, использованный Сэмюелем для игры в шашки, ма-

ло отличался от наиболее распространенного подхода к машинной игре в шахма-

ты, т.е. также опирался на изучение дерева возможностей. Сэмюелю удалось

реализовать две формы обучения: накопление и обобщение.

Из этих двух форм накопление менее интересно и менее эффективно. Оно

сводится к хранению в памяти вычислительной машины большого числа конфи-

гураций на шашечной доске из числа тех, что возникают в ходе игры. Это кон-

фигурации, которые реально имели место и, следовательно, были представлены в

корневой вершине дерева (в отличие от гипотетических конфигураций, пред-

ставленных в остальных частях дерева).

Вместе с каждой конфигурацией в памяти хранилась также ее числовая

оценка, которая получалась путем построения дерева, применения с.о.ф. к тер-

минальным вершинам и передачи значений вверх по дереву посредством мини-

максной процедуры. Такая оценка в общем случае отличается от оценки, полу-

ченной путем непосредственного применения с.о.ф. и оказывается более полез-

ной при определении хода в игре.

Имея в памяти некоторое множество конфигураций вместе с их оценками,

программа в процессе работы ищет соответствие между конфигурацией, отве-

чающей каждой из вершин дерева, и конфигурациями из числа запомненных.

Если такое соответствие установлено, то хранимая в памяти оценка передается в

эту вершину – в результате отпадает необходимость строить какое-либо подде-

рево, которое могло бы возникнуть под этой вершиной Несомненным преимуще-

ством накопления следует считать экономию времени, поскольку накопление по-

зволяет избежать построения некоторых поддеревьев. Это одна из форм прямого

усечения дерева. Существует, однако, определенная связь между временем вы-

числения и качеством игры, поскольку размер дерева ограничивается отпущен-

ным временем. Таким образом, накопление либо обеспечивает экономию време-

ни, либо позволяет достичь лучшего качества игры за то же время путем исполь-

зования большего дерева.

Отметим еще одно обстоятельство, благодаря которому использование на-

копления улучшает качество игры. Когда находится соответствие между какой-

либо вершиной и конфигурацией из списка хранимых в памяти, в вершину пере-

носится оценка, сформированная тогда, когда данная конфигурация находилась в

корневой вершине и под ней имелось целиком все дерево возможностей. Следо-

вательно, эта оценка основывается на большем дереве, чем-то, которое было бы

сформировано под указанной вершиной, если бы такого соответствия не обна-

ружилось. И хотя с точки зрения вычислительных затрат накопление и представ-

ляет собой форму усечения, оно влияет на результат поиска так, словно ветви де-

рева там, где накопление использовалось, оказываются длиннее, чем они были

бы в отсутствие накопления.

Безусловно, размер списка конфигураций, который может храниться в па-

мяти и использоваться, ограничен сверху. Не все конфигурации, встречающиеся

в игре, могут храниться в памяти, и нужно, чтобы этот список не был перегружен

конфигурациями, которые вряд ли когда встретятся.

Другая форма обучения, использованная Сэмюелем, – обобщение. Оно по-

зволяет программе в ходе игры улучшать свою с.о.ф.

Обычно с.о.ф. представляет собой полином; в простейшем виде это поли-

ном первой степени, или взвешенная сумма, скажем s, которая вычисляется сле-

дующим образом:

...

332211

= akakaks

где а

, а

и т.д. – величины различных вычисляемых критериев, таких, как мате-

риальное соотношение, подвижность, контроль центра и пр. Они взвешиваются

по отношению друг к другу с помощью коэффициентов k

, k

, ... . Полином мо-

жет быть также и более высокой степени относительно переменных а

, например:

...

212,1

11,12211

++++= aakakakaks

но для иллюстрации метода достаточно рассмотреть случай полинома первой

степени. Качество игры зависит от подходящего выбора величин коэффициентов

, k

, ... и обобщение является средством их подгонки, обеспечивающей улуч-

шение игры. Метод обобщения представляет собой пример оптимизации с ис-

пользованием процедуры, часто называемой подъемом на гору. Имеется на-

чальный набор значений k

, k

, ... и в каждый момент времени эти коэффициенты

определяют рабочую точку. Рабочая точка перемещается в пределах многомер-

ного пространства по мере подгонки величин k

, в поисках положения, в котором

оптимизируется, определенная реакция, или целевая функция. Термин «подъем

на гору» взят здесь потому, что альпинист аналогичным образом изменяет свое

положение в двух измерениях (по широте и долготе), чтобы максимизировать

свою высоту.

Чтобы воспользоваться методом подъема на гору, следовало бы дать про-

грамме возможность сыграть некоторое количество игр с определенным партне-

ром, выбрав какое то начальное множество коэффициентов k

, а затем сыграть

еще некоторое количество игр, сделав пробное изменение в положении рабочей

точки. Таким пробным изменением могло бы быть незначительное увеличение

значения k

. Если программа во втором множестве игр выигрывает чаще, чем в

первом, го принимается новое значение k

; в противном случае происходит воз-

вращение к старой величине и производится какое то другое пробное изменение.

Очевидно, что при любом методе, зависящем от результатов всей игры в

целом, надо двигаться очень и очень медленно. Поскольку партнер, по всей ви-

димости, не может играть абсолютно ровно, необходимо, чтобы два указанных

множества игр были большими, однако при этом возникают свои трудности. Бы-

ло бы лучше найти средство для подбора величин k

в ходе ведения игры. И Сэ-

мюэль придумал, как это сделать.

Предложенный им способ основан на том, что качество игры программы

растет с глубиной просмотра возможностей. Кроме того, работа программы с

ростом глубины просмотра все в меньшей степени зависит от точного вида с.о.ф.

Таким образом, оценка конфигурации, получаемая в результате передачи оценок

вверх по дереву возможностей, в некотором смысле оказывается «лучше», чем

оценка, получаемая в результате прямого применения с.о.ф.

Если может быть найдено средство вычисления с.о.ф., обеспечивающее

четкое совпадение между переданным назад по дереву значением для каждой

конфигурации и результатом прямого применения с.о.ф. к той же самой конфи-

гурации, то такая оценка должна быть равнозначна изучению всего полностью

построенного дерева игры. В методе обобщения осуществляется подбор таких

коэффициентов k

, которые улучшают соответствие между результатом прямого

применения с.о.ф. и результатом использования той же самой с.о.ф., переданным

вверх по дереву возможностей.

Если s – результат прямой оценки с помощью с.о.ф., a S

– результат пере-

дачи оценки по дереву, то можно считать их разность ошибкой е, где

sse

−

Сэмюэль сделал так, что в ею программе вычисляется текущая корреляция

между е и а

, а

и т.д., положительная корреляция между е и любым значением а,

указывает, что соответствующий коэффициент k

, следует уменьшить, а отрица-

тельная корреляция означает, что его надо увеличивать.

При применении рассматриваемого метода требуется уделить внимание

обеспечению его устойчивости, так как можно получить схему, к бесконечному

«рысканию» вокруг оптимума. Окончательный вариант, используемый Сэмю-

элем, не дает плавного приближения к оптимуму, свойственного процедуре

подъема на гору. В нем после каждого хода производится весьма существенное

изменение величин коэффициентов k

Несмотря на сказанное о преимуществах, которые ожидаются от хорошего

согласования прямого применения с.о.ф. с переданными назад по дереву величи-

нами, из такого согласования не обязательно вытекает хорошая игра. Идеальное

согласие наблюдалось бы и в том случае, если все k

, положить равными нулю.

Но это, очевидно, никак не может привести к хорошей игре. На самом деле при

любом множестве k

, обеспечивающем хорошее качество игры, можно обратить

все знаки k

и получить очень слабую игру (фактически игру в поддавки). Однако

согласие между двумя типами оценок при этом будет столь же хорошим, как и

для первоначальных значений k

Метод позволяет прийти к состояниям, которые обеспечивают хорошее со-

гласие, но слабую игру. Чтобы избежать такой ситуации, коэффициент при од-

ном из членов с.о.ф. был зафиксирован и приравнен некоторой положительной

величине (скажем единице), тогда как другие коэффициенты изменялись. Выде-

ленный член был связан с оценкой материального соотношения, поскольку ра-

зумно предполагать, что игроку всегда выгодно, чтобы его шашки на доске со-

хранялись.

Люди подходят к решению таких задач, как шахматные, исходя из своего

жизненного опыта и навыков, приобретенных за многие годы жизни. Едва ли

стоит убеждать человека, что он должен стараться сохранять свои фигуры и за-

хватывать фигуры противника – эту мысль он усвоил еще в детстве, когда спо-

рил с товарищами из-за игрушек. Однако машине это необходимо «сказать»,

сделав положительным коэффициент при члене, обеспечивающим преимущество

в фигурах.

Установив коэффициент при материальном соотношении равным единице,

мы получим следующее выражение для с.о.ф.:

...

33221

akakas

Обобщение основано на подгонке численных параметров. Процедуру под-

гонки можно использовать для выбора тех членов, которые должны быть вклю-

чены в с.о.ф. Сэмюэль держал в своей программе больший «ассортимент» крите-

риев, чем тот, что допускался до использования в конкретной с.о.ф. в каждый

момент времени. Используемое множество критериев видоизменялось самым

непосредственным образом: если какое то из значений k

оставалось близким к

нулю в течение достаточно длительного времени, то тот член с.о.ф., к которому

относится этот коэффициент, изымался из рабочего множества, а на его место

ставился другой – из числа ожидающих своей очереди. Изъятый член добавлялся

к множеству ожидающих и мог быть заново внесен в с.о.ф. позже, при другой

замене.

Возможность изменения множества членов с.о.ф. придает данному методу

обучения новый характер. Теперь его можно воспринимать как некую самоорга-

низующуюся систему. Если же действие сводится только лишь к подгонке пара-

метров, то этот термин, по-видимому, не приложим. Здесь уместнее более «сла-

бый» термин – самооптимизация. Между этими понятиями нельзя провести чет-

кую границу, поскольку, по существу, нет четкого различия между образованием

новой связи (структурное изменение) и включением усиления, благодаря кото-

рому из нуля делается конечная величина (изменение параметра). Различие, од-

нако, состоит в том, насколько легче описать систему одним из способов, чем

другим.

Описанные методы обучения обладают еще одним существенным недос-

татком: заложенная в них программа не способна «усваивать» силу или манеру

игры своего противника и реагировать на нее (если это и происходит, то лишь