Барыкин С.Г., Плотникова Н.В. Системы искусственного интеллекта

Подождите немного. Документ загружается.

для распределения входных сигналов. Каждый элемент из множества входов Х

отдельным весом соединен с каждым искусственным нейроном. А каждый ней-

рон выдает взвешенную сумму входов в сеть. В искусственных и биологических

сетях многие соединения могут отсутствовать, все соединения показаны в целях

общности. Могут иметь место также соединения между выходами и входами

элементов в слое.

Рис. 2.13. Однослойная нейронная сеть

Многослойные сети обладают большими возможностями, чем однослой-

ные, и в последние годы были разработаны алгоритмы для их обучения.

Рис. 2.14. Многослойная нейронная сеть

Многослойные сети могут образовываться каскадами слоев. Внешние слои

многослойной сети называют входным и выходным слоями. Внутренние слои

называют скрытыми. Число скрытых слоев неограниченно. Выход одного слоя

является входом для последующего слоя. Подобная сеть показана на рис. 2.14 и

изображена со всеми соединениями.

∑

Массив весовых

коэффициентов

Массив весовых

коэффициентов

Многослойные сети могут привести к увеличению вычислительной мощ-

ности по сравнению с однослойной сетью лишь в том случае, если активацион-

ная функция между слоями будет нелинейной. Любая многослойная линейная

сеть может быть заменена эквивалентной однослойной сетью, если активацион-

ная функция между слоями будет линейной

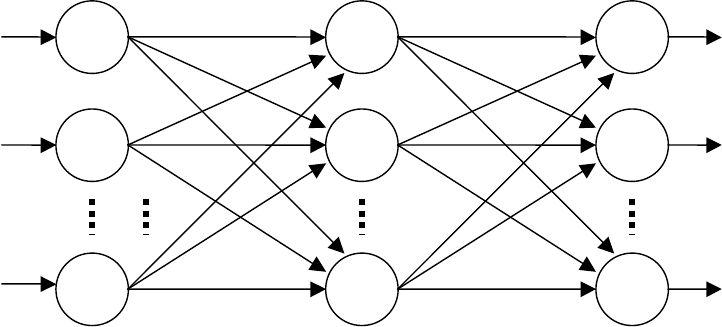
Двухслойный вариант сети с прямыми связями представлены на рис. 2.15.

Характерной особенностью таких сетей является равенство числа нейронов по

слоям и, кроме того, все нейроны входного слоя активизируются вектором вход-

ного сигнала, а все нейроны выходного слоя определяют выходной вектор.

Рис. 2.15. Двухслойная сеть с прямыми связями

В общем случае в многослойных сетях произвольной структуры возможны

различные конфигурации перекрестных связей. Вариант двухслойной сети с пе-

рекрестными связями приведен на рис. 2.16. Как видно из этого рисунка, нейро-

ны второго слоя имеют настраиваемые синаптические связи, как с выходов ней-

ронов первого слоя, так и непосредственно с устройства ввода нейрокомпьютера.

В общем случае в многослойных сетях произвольной структуры возможны

различные конфигурации перекрестных связей.

У сетей без обратных связей нет памяти, их выход полностью определяется

текущими входами и значениями весов. В некоторых конфигурациях сетей с об-

ратными связями предыдущие значения выходов возвращаются на входы; выход,

следовательно, определяется как текущим входом, так и предыдущими выхода-

ми. По этой причине сети с обратными связями могут обладать свойствами,

сходными с кратковременной человеческой памятью, сетевые выходы частично

зависят от предыдущих входов.

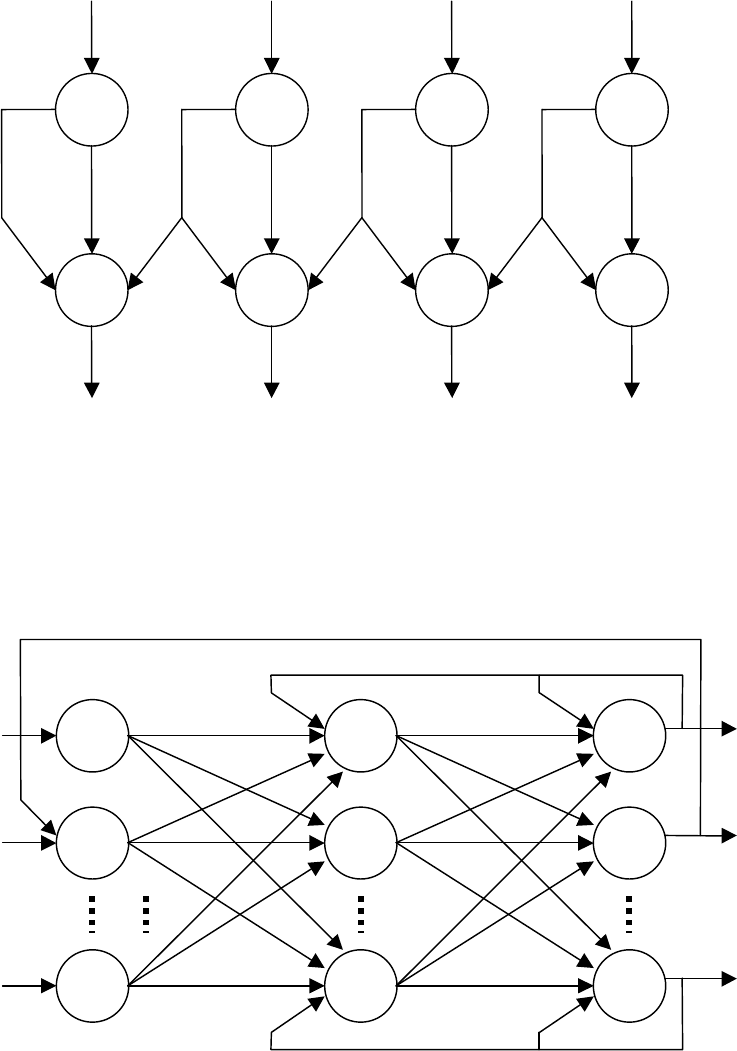
Введение обратных связей в НС как и в любую другую динамическую

систему, существенно меняет ее функциональные возможности. Обратной свя-

зью можно охватывать как отдельный слой так и несколько слоев и даже всю

сеть. На рис. 2.17 представлена двухслойная сеть с различными обратными свя-

зями.

Рис.2.16. Двухслойная сеть с перекрестными связями

Рис. 2.17. Двухслойная сеть с обратными связями

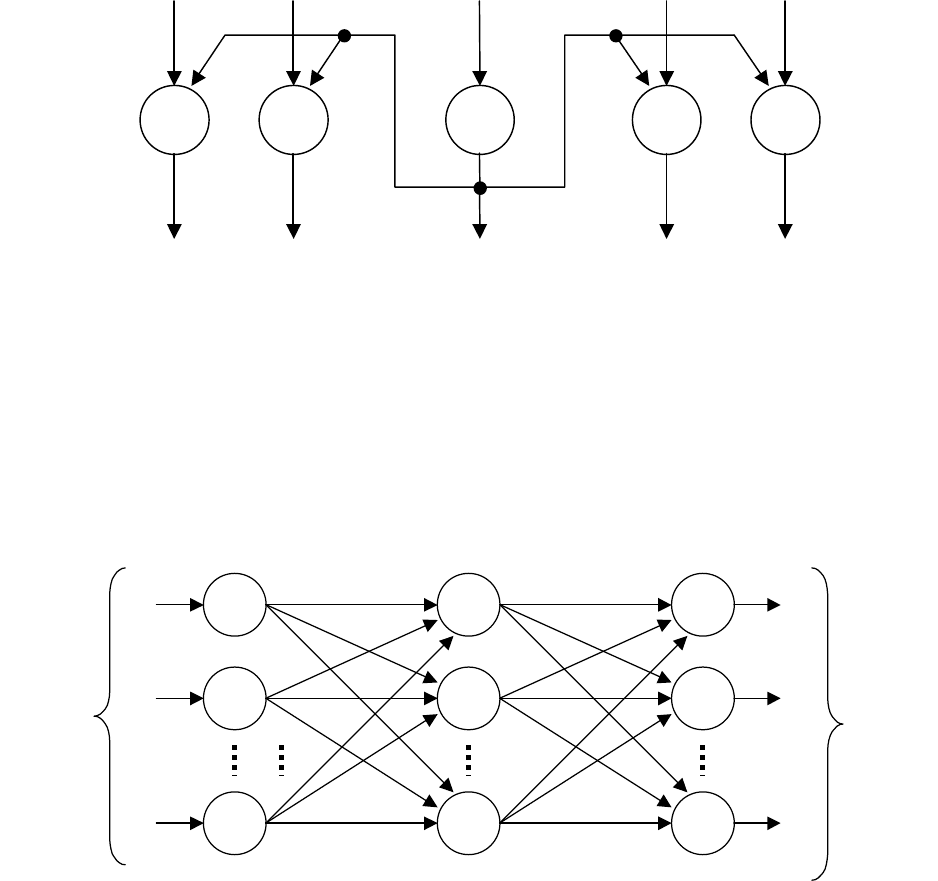
Сеть с латеральными связями. Введение в скрытые слои нейронной сети

латеральных связей позволяет контрастировать изображение на случайном фоне,

что повышает эффективность распознавания графических образов. Латеральные

связи бывают тормозящими и возбуждающими. В живой природе эти связи до-

вольно частое явление. На рис. 2.18 показан пример контрастирования сигналов

соседних нейронов в отдельном слое. Подавая сигналы через отрицательные ко-

эффициенты синаптической связи с центрального нейрона на два левых, доби-

ваются снижения активности этих нейронов. Подача сигналов на два правых

нейрона через положительные коэффициенты синаптической связи увеличивает

степень активности этих нейронов. В результате центральный и два правых ней-

рона будут значительно активнее двух левых, что эквивалентно повышению кон-

трастности входного образа (входного изображения).

Рис.2.18. Слой нейронной сети с латеральными связями

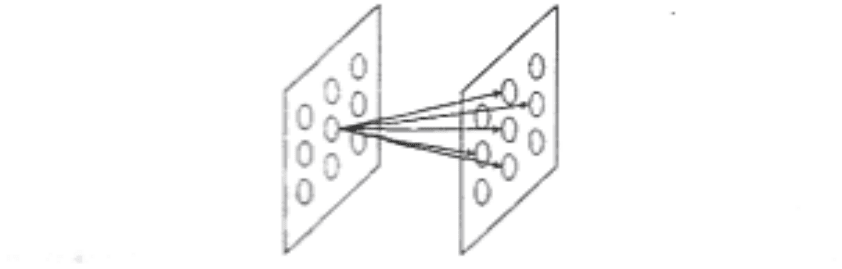
При решении задачи распознавания широко используют многослойные се-

ти, в которых каждый нейрон текущего слоя связан с каждым нейроном сле-

дующего слоя (рис. 2.19). Такой подход доказал свою работоспособность в раз-

личных практических применениях, но у него есть один недостаток – большая

избыточность нейронных связей.

Рис. 2.19. Одномерная полносвязная двухслойная сеть

Может получиться сеть с топологией, показанной на рис. 2.20. Здесь каж-

дый нейрон своими синаптическими связями проецируется на небольшую об-

Входные

сигналы

Выходные

сигналы

ласть следующего слоя. Для наглядности слои этой сети стоит представлять не

одномерными, a двухмерными.

Рис. 2.20. Нейронная

сеть с двухмерными

нейронными слоями

2.3.3. Математическое описание нейронных сетей

На основе математической модели одиночного нейрона (2.3) можно соста-

вить математическое описание (математическую модель) всей нейронной сети.

Рассмотрим некоторые из них:

Однослойная нейронная сеть:













++=

∑

kkki

wtxwwfty

1010

)()(

(2.8)

Двухслойная нейронная сеть с прямыми связями:

























++=

∑∑

kkkiii

wtxwfwwfty

10112202

)()(

(2.9)

Двухслойная сеть с перекрестными связями:

























∑∑∑

ikkii

txwwtxwfwfty

101122

)()()(

(2.10)

Выражение (2.10) описывает двухслойную сеть с полными перекрестными

связями.

Приняты следующие обозначения:

I = 1, 2, ..., N – число нейронов второго слоя; k = 1,2, ..., K – число нейронов

первого слоя; f

, f

– функции активации нейронов первого и второго слоев: w

10k

–

начальное возбуждение i-го нейрона первого слоя; w

20k

- начальное возбуждение

k-го нейрона второго слоя; w

, w

– весовые коэффициенты i-го нейрона второго

слоя и k-го нейрона первого слоя; y

(t) – i-я координата выходного вектора: x

(t) –

k-я координата входного вектора. В общем случае K

≠

N. Предполагается также,

что функции активации нейронов одного слоя одинаковые.

При решении одной и той же задачи сеть с перекрестными связями, как

правило, значительно проще сети с прямыми последовательными связями по

числу нейронов, используемых в сети.

Сеть с обратными связями:

∑

−+=

tbytxwfty

))1()(()(

, (2.11)

где b – синаптический коэффициент обратной связи; y(t–l) – значение выходного

сигнала нейрона в момент времени (t–1); n – число входов нейрона. Для двух-

слойной сети, имеющей N нейронов во втором слое и K нейронов в первом, ма-

тематическая модель имеет вид:

∑∑ ∑ ∑

== ===

−+−+−+=

iikkkkki

tybtybtxbxwfwfty

1,11

2211122

))1())1())1(((()(

(2.12)

Здесь b

2ik

– синаптические коэффициенты обратной связи с выходов ней-

ронов второго слоя на входы нейронов первого слоя: b

– коэффициенты обрат-

ной связи с выходов нейронов второго слоя на входы нейронов второго слоя; b

– коэффициенты обратной связи нейронов первого слоя. Остальные обозначения

такие же, как в выражениях (2.9) и (2.10).

2.3.4. Архитектура связей

На способ обработки информации решающим образом сказывается нали-

чие или отсутствие в сети петель обратных связей. Если обратные связи между

нейронами отсутствуют, обработка информации в сети однонаправлена. Входной

сигнал обрабатывается последовательностью слоев и ответ гарантированно по-

лучается через число тактов равное числу слоев (табл. 2.1).

Наличие же обратных связей может сделать динамику нейросети (называе-

мой в этом случае рекуррентной) непредсказуемой. В принципе, сеть может «за-

циклиться» и не выдать ответа никогда. Причем не существует алгоритма, по-

зволяющего для произвольной сети определить, придут ли когда-либо ее элемен-

ты в состояние равновесия.

Вообще говоря, то, что нейроны в рекуррентных сетях помногу раз прини-

мают участие в обработке информации позволяет таким сетям производить более

разнообразную и глубокую обработку информации. Но в этом случае следует

принимать специальные меры к тому, чтобы сеть не зацикливалась. Например,

ограничивать число итераций.

2.3.5. Задачи оптимизации при обучении нейронной сети

Пусть имеется нейронная сеть, выполняющая преобразование F: X→Y век-

торов Х из признакового пространства входов Х в вектора Y выходного простран-

ства

Y. Сеть находится в состоянии W из пространства состояний W. Пусть далее

имеется обучающая выборка (X

, Y

= 1… p. Рассмотрим полную ошибку Е,

делаемую сетью в состоянии W

()

(

)

[

]

∑∑∑

−=−==

αα

αααα

YWXFYWXFWEE .;;)(

(2.13)

Таблица 2.1

Сравнение архитектур связей нейросетей

Сравнение

сетей

Без обратных связей

(многослойные)

С обратными связями

Преимущества

Простота реализации.

Гарантированное получение

ответа после прохождения

данных по слоям

Минимизация размеров сети – нейроны

многократно участвуют в обработке дан-

ных. Меньший объем сети облегчает про-

цесс обучения

Недостатки

Требуется большее число

нейронов для алгоритмов

одного и того же уровня

сложности. Следствие –

большая сложность обу-

чения

Требуются специальные условия, га-

рантирующие сходимость вычислений

Отметим два свойства полной ошибки. Во-первых, ошибка E = E(W) явля-

ется функцией состояния W, определенной на пространстве состояний. По опре-

делению, она принимает неотрицательные значения. Во-вторых, в некотором

обученном состоянии W*, в котором сеть не делает ошибок на обучающей вы-

борке, данная функция принимает нулевое значение. Следовательно, обученные

состояния являются точками минимума введенной функции E(W).

Таким образом, задача обучения нейронной сети является задачей поиска

минимума функции ошибки в пространстве состояний W и для ее решения могут

быть использованы стандартные методы теории оптимизации.

Привлекательной чертой является единый принцип обучения нейросетей –

минимизация эмпирической ошибки. Функция ошибки, оценивающая данную

конфигурацию сети, задается извне – в зависимости от того, какую цель пресле-

дует обучение. Далее сеть начинает постепенно модифицировать состояние всех

своих синаптических весов таким образом, чтобы минимизировать эту ошибку.

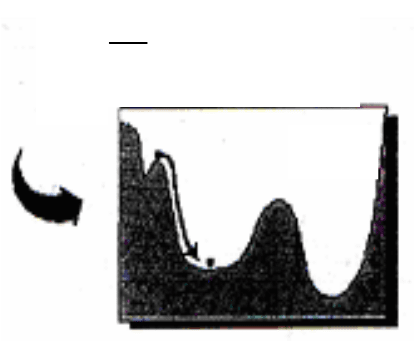
Образно этот процесс можно представить себе как поиск минимума функ-

ции ошибки E(w), зависящей от набора всех синаптических весов сети W (рис.

2.21).

Базовой идеей всех алгоритмов обучения является учет локального гради-

ента в пространстве конфигураций для выбора траектории быстрейшего спуска

по функции ошибки. Функция ошибки, однако, может иметь множество локаль-

ных минимумов, представляющих суб-оптимальные решения. Поэтому гради-

ентные методы обычно дополняются элементами стохастической оптимизации,

чтобы предотвратить застревание конфигурации сети в таких локальных мини-

мумах. Идеальный метод обучения должен найти глобальный оптимум конфигу-

рации сети.

()

−∇=

Рис. 2.21. Обучение сети как зада-

ча оптимизации

Различают алгоритмы обучения нейросетей с учителем и без учителя.

Сеть обучается, чтобы для некоторого множества входов давать желаемое

(или, по крайней мере, сообразное с ним) множество выходов. Каждое такое

входное (или выходное) множество рассматривается как вектор. Обучение осу-

ществляется путем последовательного предъявления входных векторов с одно-

временной подстройкой весов в соответствии с определенной процедурой. В

процессе обучения веса сети постепенно становятся такими, чтобы каждый

входной вектор вырабатывал выходной вектор. Нейронные сети сами моделиру-

ют себя в результате попыток достичь лучшей модели поведения.

Ошибка сети зависит от конфигурации сети – совокупности всех ее синап-

тических весов. Но эта зависимость не прямая, а опосредованная. В общем виде

функция ошибки имеет вид:

{

}

),(,,)(

ααα

xyyxEwE =

. (2.14)

Здесь

{

}

αα

yx ,

– набор примеров (т.е. пар входов-выходов), на которых

обучается нейросеть, а

(

)

{

}

wxy ,

– реальные значения выходов нейросети, зави-

сящие от конкретных значений ее синаптических весов. Такой способ обучения,

когда действительный выход нейросети сравнивают с эталонным, называют обу-

чением с учителем.

Векторы обучающего множества предъявляются последовательно, вычис-

ляется ошибка, веса подстраиваются для каждого вектора в соответствии с алго-

ритмом, стремящимся минимизировать ошибку, до тех пор, пока ошибка по все-

му обучающему массиву не достигнет приемлемо низкого уровня.

Возможен режим обучения, при котором желаемые значения выходов во-

обще неизвестны, и сеть обучается только на наборе входных данных

{

}

(

)

{

}

wxyxEwE ,,)(

αα

. (2.15)

Такой режим обучения сети называют обучением без учителя.

Обучающий алгоритм подстраивает веса сети так, чтобы получались согла-

сованные выходные векторы, т. е. чтобы предъявление достаточно близких

входных векторов давало одинаковые выходы. Процесс обучения, следователь-

но, выделяет статистические свойства обучающего множества и группирует

сходные векторы в классы. В этом случае сети предлагается самой найти скры-

тые закономерности в массиве данных (табл. 2.2).

Таблица 2.2

Сравнение режимов обучения нейросетей

Вид обучения С «учителем» Без «учителя»

Что подается в каче-

стве обучающих при-

меров

Набор пар «входов-выходов»

{

}

αα

yx ,

Только набор вход-

ных значений

{

}

Что требуется от сети

Найти функцию, обобщающую

примеры, в случае дискретных

– классифицировать вхо-

ды. В целом – научиться реа-

гировать схожим образом в

схожих ситуациях

Найти закономерно-

сти в массиве данных,

отыскать порождаю-

щую данные функ-

цию распределения,

найти более компакт-

ное описание данных

С практической точки зрения, «помеченные» данные

{

}

αα

yx ,

зачастую

дороги и не столь многочисленны, как «непомеченные»

{

}

, например, в слу-

чае, когда «учителем» является человек – эксперт. В силу этого обстоятельства

на таких данных можно обучить лишь относительно простые и компактные ней-

росети. Напротив, нейросети, обучаемые без учителя часто используют для пере-

работки больших массивов «сырых» данных – в качестве предобрабатывающих

фильтров.

Ограничившись лишь двумя описанными выше факторами, разделяющими

сети по типу обучения (программирования) и функционирования, получим сле-

дующую полезную классификацию базовых нейро-архитектур (табл. 2.3).

2.3.6. Обучение однослойных нейронных сетей с учителем

Персептрон – первая нейросетевая парадигма, доведенная до кибернетиче-

ской реализации. Теория персептронов является основой для многих других ти-

пов искусственных нейронных сетей, и персептроны иллюстрируют важные

принципы. В силу этих причин они являются логической исходной точкой для

изучения искусственных нейронных сетей.

Обучение персептрона является примером детерминистского подхода.

Детерминистский метод обучения шаг за шагом осуществляет процедуру

коррекции весов сети, основанную на использовании их текущих значений, а

также величин входов, фактических выходов и желаемых выходов.

Таблица 2.3

Классификация нейросетей

Тип обучения

Тип связей

С «учителем» Без «учителя»

Без обратных связей

Многослойные

персептроны

(аппроксимация функций,

классификация)

Соревновательные сети,

карты Кохонена (сжатие

данных, выделение при-

знаков)

С обратными связями

Рекуррентные аппрокси-

маторы

(предсказание временных

рядов, обучение в режиме

on-line)

Сеть Хопфилда

(ассоциативная память,

кластеризация данных,

оптимизация)

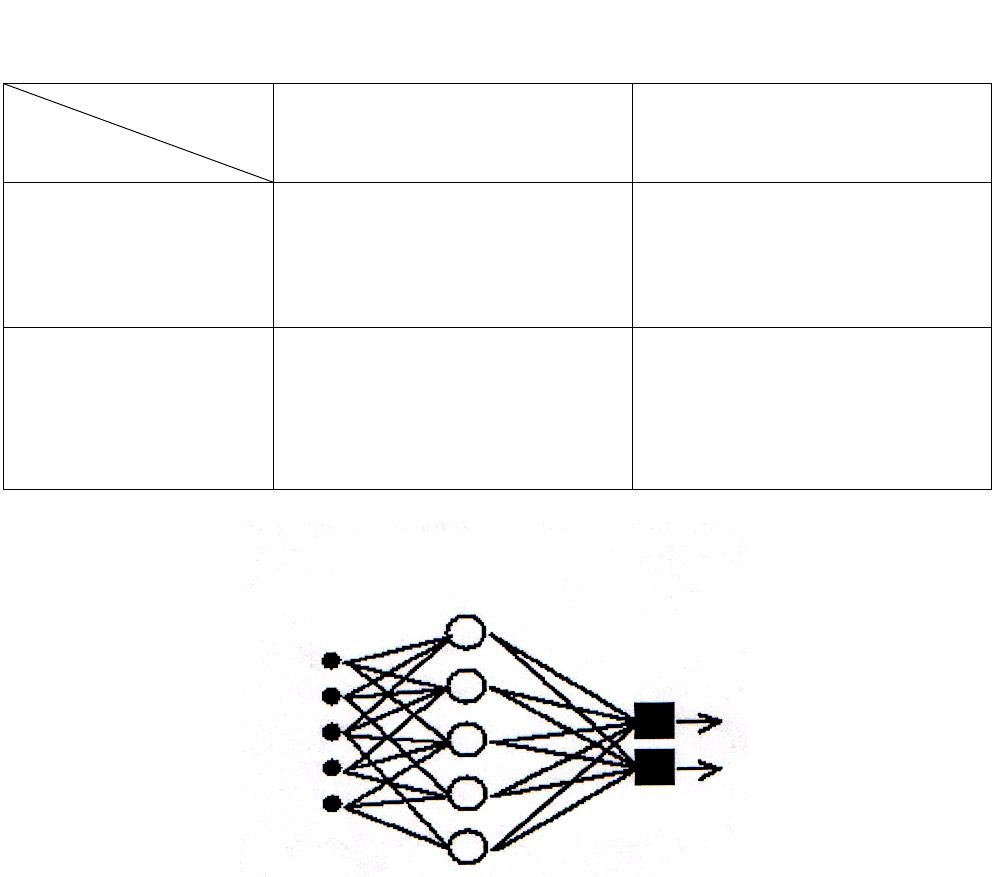
Рис. 2.22. Элементарный персептрон

Розенблатта

Простейший классический персептрон содержит нейроподобные элементы

трех типов: (рис. 2. 22) S-элементы принимают двоичные сигналы, А-элементы

выполняют нелинейную обработку информации и имеют изменяемые веса свя-

зей. R-элементы с фиксированными весами формируют сигнал реакции персеп-

трона на входной стимул.

Подавляющее большинство приложений связано именно с применением

многослойных персептронов. Как правило, используются именно сети, состоя-

щие из последовательных слоев нейронов.

-элементы

A-элементы

-элементы