Baumgarte T., Shapiro S. Numerical Relativity. Solving Einstein’s Equations on the Computer

Подождите немного. Документ загружается.

5.2 Hydrodynamics 161

0.1

0.05

0.1

0.05

−0.05

−0.1

−0.05

−0.1

−0.2

t /(2π/k)

dP/(P

)

/(B

) dv

/ h

0.2

0.1

(a)

(b)

(c)

468

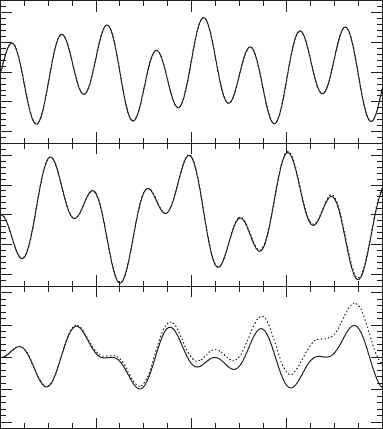
Figure 5.4 Analytic and numerical solutions for the perturbations of a magnetized ﬂuid due to the presence of a

linear, standing gravitational wave. The thick solid and thin dotted lines represent, respectively, the analytic and

numerical solutions, though the two lines are not readily distinguishable in plots (a) and (b). All quantities are

evaluated at z = 1/8 and are normalized as indicated. Time is normalized by the gravitational wave period.

[From Duez et al. (2005b).]

smaller gravitational wave strength leads to a smaller discrepancy with the analytic solution,

as was also demonstrated. Finally, the various MHD modes were extracted from the output

via velocity projections and the code was shown to correctly represent all three MHD

waves, plus the contribution from the particular solution.

It is not trivial to devise a simple test problem to calibrate the ability of a general

relativistic code to evolve an electromagnetic ﬁeld in a strongly-gravitating, dynamical

spacetime in which a black hole forms. It is harder still to devise for such a spacetime a

problem that calibrates a code’s performance both in the highly conducting MHD regime

and the nonconducting vacuum regime. But consider the following scenario for the col-

lapse of a magnetized spherical star to a black hole: Adopt the approximation that the

electromagnetic ﬁelds are sufﬁciently weak that the matter and gravitational ﬁelds can be

described by the unperturbed Oppenheimer–Snyder solution for the collapse of a spheri-

cal, homogeneous dust ball to a Schwarzschild black hole (see Chapter 1.4.) Assume the

matter to be perfectly conducting and threaded by a nearly uniform interior and a dipole

exterior magnetic ﬁeld at the onset of collapse. Determine the subsequent evolution of

the interior and exterior magnetic and electric ﬁelds without approximation: calculate the

ﬁelds analytically in the matter interior, assuming the MHD equations, and numerically in

162 Chapter 5 Matter sources

the vacuum exterior. Apply the familiar electromagnetic junction conditions to match the

ﬁelds across the stellar surface at each instant of time in order to determine the inner

boundary conditions for the integration of exterior electromagnetic ﬁelds.

Exercise 5.35 Here we seek the relativistic generalization of Newtonian initial data

describing a uniformly magnetized dust ball of radius R, matched onto an exterior

dipole magnetic ﬁeld. In orthonormal spherical polar coordinates, the Newtonian

interior is characterized by the constant magnetic ﬁeld

= B(cos θ,−sin θ,0), (Newtonian interior) (5.183)

assuming the ﬁeld is aligned with the z-axis, while the exterior is a pure dipole ﬁeld

given by

(cos θ,

sin θ,0) (Newtonian exterior). (5.184)

The junction conditions on the surface of the star require that the normal (i.e., radial)

component of the ﬁeld be continuous across the stellar surface. The tangential

discontinuity in B

implies the presence of a surface current.

(a) Use the OS interior metric (1.88) to show that a relativistic generalization of the

uniform interior ﬁeld may be speciﬁed by

ˆχ

= B cos θ



sin χ





sin χ



−2

, (5.185)

=−B sin θ



sin χ



sin χ



−2

. (5.186)

In particular, show that the above ﬁeld satisﬁes the constraint D

= 0 and reduces

to the uniform interior Newtonian ﬁeld in stars of low compaction.

(b) Use the Schwarzschild metric (1.51) together with Maxwell equations (5.142)

and (5.143) in vacuum to show that the relativistic generalization of the dipole

exterior ﬁeld is given by

=−

6µ

cos θ



ln(1 − x

−1

) + (1 + x

−1

/2)



, (5.187)

6µ

cos θ



(1 − x

−1

)

1/2

ln(1 − x

−1

) +

1 − x

−1

(1 − x

−1

)

1/2



. (5.188)

Here r

is the Schwarzschild (areal) radius, x

≡ r

/(2M), and µ

is the magnetic

dipole moment.

Hint: Introduce a vector potential A

via F

=∇

−∇

and solve for A

for

an exterior vacuum dipole ﬁeld in axisymmetry.

is given by

=−B



ln(1 − X

−1

) + (1 − X

−1

/2)



−1

, (5.189)

Wasserman and Shapiro (1983).

5.3 Collisionless matter 163

where R

and X

are the values of r

and x

on the stellar surface, and where B is

the factor appearing in equations (5.185)and(5.186).

Exercise 5.36 Show that the evolution of the interior magnetic ﬁeld in exercise 5.35

is given analytically by equations (5.185)and(5.186) all during OS collapse, pro-

vided the parameter B varies with proper time τ according to

B(τ ) = B



(τ )

(0)



2/3

, (5.190)

where ρ

(τ ) is given by equation (1.96).

The solution to the “magnetized OS collapse” problem formulated above has been

determined

and this simple scenario has been used to experiment with several alternative

time slicing conditions for handling black hole formation and the associated appearance

of singularities. The choice of time slicing is important for enabling the evolution of the

exterior electromagnetic ﬁeld to late times. The choices considered ranged from “singu-

larity avoiding” time coordinates, like maximal time slicing, to “horizon penetrating” time

coordinates, like Kerr–Schild slicing, accompanied by “black hole excision”.

The latter

choice allows for the integraton of the exterior electromagnetic ﬁelds arbitrarily far into

the future. At late times the longitudinal magnetic ﬁeld in the exterior transforms into

a transverse electromagnetic wave; part of the electromagnetic radiation is captured by

the hole and the rest propagates outward and escapes. The ﬁeld pattern at various times

is shown in Figures 5.5 and 5.6. The electromagnetic ﬁeld strength at a ﬁxed exterior

radius dies out as t

−4

, which agrees with the t

−(2l+2)

decay rate expected from perturbation

theory

and applicable here to an l = 1 dipole ﬁeld threading a spherical star undergoing

gravitational collapse (see Figure 5.7).

5.3 Collisionless matter

Several important astrophysical systems are made up of particles of collisionless matter. In

such systems, the mean-free-path for particle-particle interactions is much longer than the

scale of the system. Equivalently, the mean time for particle collisions is much longer than

the dynamical or “crossing” time scale of the system, i.e., the time it takes for a particle to

cross from one side of the system to the other. Systems of particles obeying this condition

are in the opposite limit from the hydrodynamical gases we treated above. One example of

a collisionless system is a star cluster, a large, self-gravitating, N -body system in which the

individual particles – the stars – interact exclusively via gravitation. In the strictly collision-

less limit, a cluster of ﬁnite total mass is treated as an inﬁnite swarm of point particles, each

of inﬁnitesimal mass. The stars then move in the smooth, background gravitational ﬁeld

Baumgarte and Shapiro (2003a).

For a discussion of black hole excision during stellar collapse, see Chapter 14.2.3.

Price (1972b).

164 Chapter 5 Matter sources

t/ M = 0.00

t/ M = 9.4

t/ M = 12.9

t/ M = 11.9

t/ M = 74.8

t/ M = 131.6

Figure 5.5 Snapshots of the exterior magnetic ﬁeld lines on select Kerr–Schild time slices for a homogeneous,

conducting dust ball of mass M that collapses from rest from an initial areal radius R

(0) = 4M. Points are

plotted in a meridional plane in areal radius. The white shaded sphere covers the matter interior; the black shaded

area covers the region inside the event horizon; the gray shaded area covers the region inside r

= M that is

excised from the numerical grid once the surface passes inside. The initial growth of the (longitudinal) ﬁeld is

due to ﬂux freezing in the interior and is followed by a burst of (transverse) electromagnetic radiation in the

vacuum exterior once the surface approaches the horizon at r

= 2M. In this time coordinate, using excision, the

exterior electromagnetic ﬁeld can be evolved reliably to arbitrary late times. By the end of the integration, all

exterior electromagnetic ﬁelds in the vicinity of the black hole have been captured or radiated away. [From

Baumgarte and Shapiro (2003a).]

established by their cumulative, smooth mass-energy distribution. In reality, the distribution

of stars in a cluster is not continuous, but discrete, so that the gravitational ﬁeld governing

their motion is granular. Consequently, the stars undergo stochastic, small-angle deﬂections

from their smooth orbits due the cumulative role of many distant “gravitational encoun-

ters” (i.e., small-angle, Coulomb scattering). Very occasionally, stars may even wander

close to their neighbors and experience large-angle, gravitational deﬂections. Moreover,

since stars are not point particles and have ﬁnite sizes, they can even undergo contact

collisions with other stars. Typically, gravitational scattering due to the granularity of the

gravitational ﬁeld is not important in the evolution of a large star cluster over a dynamical

(orbital) time scale, but only on a much longer, “relaxation” time scale. Physical collisions

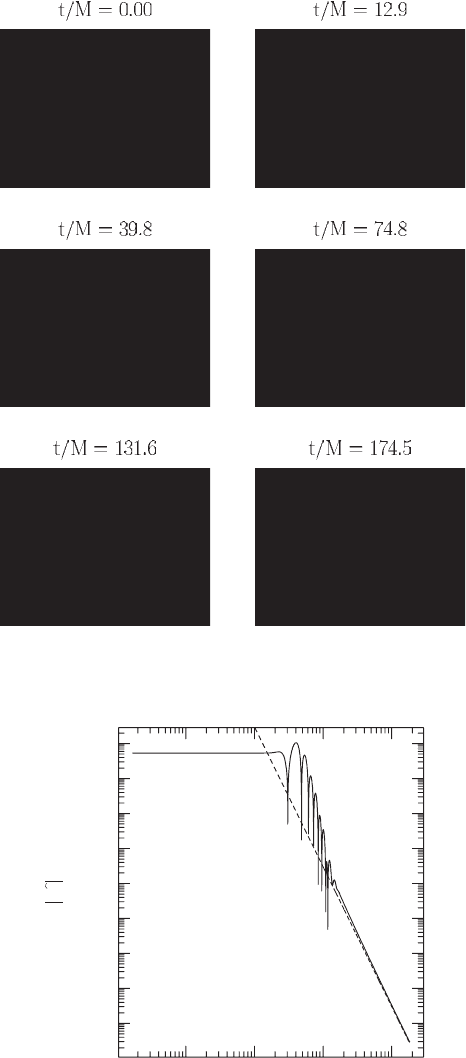
Figure 5.6 Far-zone view of the same collapse depicted in Figure 5.5. Note the transformation of the dipole ﬁeld

from a quasistatic longitudinal ﬁeld to a transverse electromagnetic wave. [From Baumgarte and Shapiro

(2003a).]

0.01

0.001

0.0001

110

−5

−6

−7

−8

−9

−10

100 1000

Figure 5.7 The absolute value of the orthonormal component of the radial magnetic ﬁeld |B

| at r

= 20M as a

function of time. The dashed line is a power law varying like t

−4

, the expected decay rate for an initial static

dipole electromagnetic ﬁeld in a spherical star undergoing collapse to a black hole. [From Baumgarte and

Shapiro (2003a).]

166 Chapter 5 Matter sources

resulting from direct impact are also unimportant on dynamical timescales in astrophysical

star clusters. For realistic systems, the star cluster may be treated as a perfectly collisionless

gas over dynamical time scales, while the effects of gravitational scattering or collisions

can be handled as perturbations if the evolution is tracked over longer, secular time scales.

Globular clusters consisting of N ∼ 10

stars, galaxies with N ∼ 10

stars and clusters

of galaxies consisting of N ∼ 10

galaxies are all familiar examples of nearly collisionless

clusters as deﬁned above. Another important example of a collisionless gas includes

cosmological “dark matter”, which comprises over 90% of the mass in the Big Bang

Universe. Dark matter halos, which might be clusters of neutrinos, neutralinos, axions, or

some other weakly interacting massive particle, are collisionless clusters. Here we shall

be particularly interested in relativistic systems. Astrophysical realizations of collisionless

relativistic systems include relativistic star clusters (including large-N clusters of compact

stars and (or) black holes) and collisionless dark matter halos consisting of relativistic

particles.

Readers may ﬁnd it useful to be familiar with the elementary principles of relativis-

tic kinetic theory before reading onward,

although the discussion below is reasonably

self-contained.

In kinetic theory, a large N -body system is described by a dimensionless phase-space

distribution function f (x

, p

). Assume for the moment that all particles in the system

have the same rest mass. Then the function f is is related to the number density of particles

in 6-dimensional phase space according to

f =

, (5.191)

where we have expressed the volume elements in physical space, d

x, and in momentum

space, d

p, in an orthonormal basis. The product d

p, as well as the distribution

function f , is a Lorentz invariant. The distribution function f satisﬁes the relativistic

Boltzmann equation,

D f

dλ

≡



dλ



∂ f

∂x



dλ



∂ f

∂p



δ f

δλ



coll

. (5.192)

Here the derivative is along the particle trajectory in phase space and λ is an afﬁne parameter

along that trajectory deﬁned so that the momentum is given by

≡

dλ

. (5.193)

For particles of ﬁnite rest mass m,wehaveλ = τ/m,whereτ is the particle proper time.

The Boltzmann equation (5.192) is a continuity equation in phase space, which says that

particles are created and destroyed along their trajectories in phase space by virtue of

See, e.g., Lightman and Shapiro (1978), Spitzer (1987), and Binney and Tremaine (1987), and references therein, for

detailed discussions of star cluster dynamics and evolution, and the role of gravitational encounters and collisions, in

Newtonian theory.

See, e.g., Misner et al. (1973), Section 22.6.

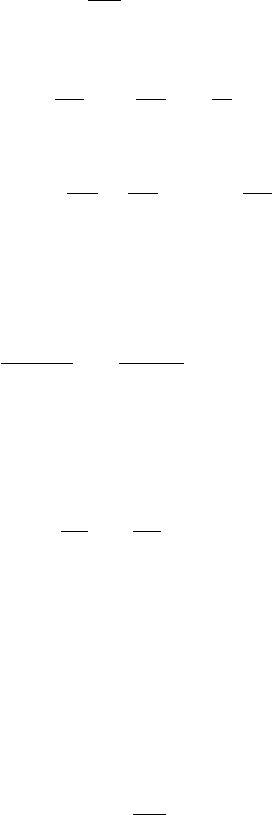
5.3 Collisionless matter 167

collisions, the rate of which is given by the term on the right hand side. Excluding all

long-range forces other than gravitation, so that the particle paths are geodesics except at

occasional points where scattering or collisions occur, we then have

dλ

=−

. (5.194)

Exercise 5.37 Show that the Boltzmann equation may be written in the form

D f

dλ

= p

D f



δ f

δλ



coll

, (5.195)

where

≡

∂

∂x

− 

∂

∂p

. (5.196)

Exercise 5.38 Derive the relativistic equation of radiation transport (5.93) from the

Boltzmann equation (5.195), accounting for photon emission and absorption.

start, use f ∝ I

/ν

to show that in an arbitrary frame the transfer equation can be

cast in the form

D(I

/ν

)



δ(I

/ν

)

δλ



coll

= e − a(I

/ν

), (5.197)

where e is an invariant source term due to photon emission and a is an invariant

sink term due to photon absorption. Setting h = 1 = c, evaluate equation (5.197)

in an inertial frame to recover the familiar form of the equation of radiation

transfer,

∂ I

∂t

+ n

∂ I

∂x

= η

− χ

, (5.198)

where we identify e as the invariant emissivity and a as the invariant absorption

coefﬁcient (opacity) according to

e = η

/ν

, a = νχ

. (5.199)

Focus now on physical scenarios in which collisions or scatterings are either absent

entirely or unimportant on time scales of interest. In that case the right hand side of

equation (5.192) may be set equal to zero; the resulting equation is usually referred to as

the collisionless Boltzmann equation,ortheVlasov equation:

D f

dλ

= 0. (5.200)

This equation shows that the distribution function in a collisionless gas is conserved

along the orbit of each particle in phase space, which is known as Liouville’s theorem.

Equation (5.200) is sometimes called the Liouville equation.

See Lindquist (1966), Castor (1972)andMihalas and Mihalas (1984) for a detailed discussion; see Shapiro and

Teukolsky (1983), Appendix I, for a brief introduction.

This result can also hold in a collisional gas, provided the collisions satisfy detailed balancing. Detailed balancing

always applies, for example, to systems in thermodynamic equilibrium.

168 Chapter 5 Matter sources

Let us cast the Liouville equation in a form most suitable for treating a swarm of

collisionless particles with a wide distribution of masses.

Consider a small group of

particles near a particular event x

in spacetime, with 4-momentum near a particular value

. As seen in its own rest frame, this group occupies a 3-dimensional volume d

in physical space and a 4-dimensional volume d

in momentum space. In a general

coordinate basis, d

and d

are given by

√

−gdx

(5.201)

−dp

√

−g

dmdp

√

−g

, (5.202)

where m =−(p

)

1/2

is the rest-mass of a particle with 4-momentum p

.Inderiving

the second equality for d

, we differentiated this “mass hyperboloid” relation to write

mdm =−p

, which we then substituted into the ﬁrst equality to change variables from

to m. If there are dN particles in the group, then the number density in phase space, or

distribution function, F is deﬁned by

F(x

, p

) =

. (5.203)

It is often convenient to specify a point in phase space by the the set of coordinates (x

, p

This set is particularly useful whenever the spacetime possesses a Killing vector ξ

,in

which case the scalar p

is conserved along geodesics. When the Killing vector is a

coordinate basis vector, say ∂

, then the component of p

along that basis vector, p

,is

a constant of the motion. Sometimes it is useful to employ other coordinate sets, such as

, p

, m).

For collisionless matter, the particles move along geodesics and the distribution function

satisﬁes the Liouville equation in the form

dτ

F = 0, (5.204)

where the Liouville operator

D/dτ represents differentiation with respect to proper time

along the trajectory of a particle in phase space:

dτ

≡



dτ



∂

∂x



dτ



∂

∂p

∂

∂x

−

∂g

∂x

∂

∂p

. (5.205)

The smoothed-out stress-energy tensor of a cluster of particles is determined by the

distribution function according to







. (5.206)

Our discussion is patterned after Ipser and Thorne (1968).

5.3 Collisionless matter 169

The smoothed-out gravitational ﬁeld of the cluster of particles is given by the met-

ric g

, which, as always, is a solution of Einstein’s equations G

= 8π T

.Tosolve

the ﬁeld equations in 3 + 1 form we need the matter source terms given by equa-

tions (5.1)–(5.2), which are computed as quadratures over the distribution function F,using

equation (5.206).

Exercise 5.39 Show that the source terms are given by

ρ =



m(W

F)d

, (5.207)



m(Wu

F)d

, (5.208)



m(u

F)d

, (5.209)

S = ρ −



mFd

, (5.210)

where W is deﬁned in equation (5.11).

For many calculations, it is adequate to consider systems in which all the particles

have the same rest mass, m

. The reason is that, according to the equivalence principle,

all particles follow the same geodesic paths, regardless of their mass, so this is not a

physically signiﬁcant restriction for a collisionless gas. There are several equivalent ways

of restricting our general description to particles of the same rest mass. One way is to

write

F(x

, p

) = f (x

, p

)δ(m − m

). (5.211)

The resulting 4-dimensional quadratures over F that determine the matter source terms

now reduce to 3-dimensional quadratures over f . For example, inserting the the right hand

side in equation (5.202)ford

gives

ρ = m



f )



W γ

1/2



, (5.212)

and similarly for the other source terms. This is equivalent to demanding that the invariant

4-dimensional volume, d

, in momentum space obey the constraint −p

= m

,which

allows us to generate an invariant, 3-dimensional volume in momentum space,



δ[(−p

)

1/2

− m

] =





(−g)

1/2

W γ

1/2

, (5.213)

where the integral is over dp

. When we now employ d

to integrate over the phase-space

distribution function f , deﬁned by

f (x

, p

) =

, (5.214)

170 Chapter 5 Matter sources

(recall equation 5.191), the stress-energy tensor deﬁned in equation (5.206) becomes







, (5.215)

and the quadratures for the matter sources reduce to the form given in equation (5.212).

Exercise 5.40 Show that when the collisionless gas consists of a single mass species,

the Liouville equation (5.204) reduces to

∂ f

∂t





∂ f

∂x





∂ f

∂p

= 0 (5.216)

or, explicitly,

∂ f

∂t

∂ f

∂x

−

∂g

∂x

∂ f

∂p

= 0. (5.217)

For stationary spacetimes, the distribution function of a collisionless gas is independent

of time and must be a function of the dynamical constants (or “integrals”) of orbital

motion. Likewise, any function of the constants of the motion yields a stationary solution

of the collisionless Boltzmann equation. This result is often quoted as Jeans’ theorem. This

proposition is not surprising, looking at equation (5.216), since any f that is a function only

of the momenta p

conjugate to the Killing vectors ξ

in the spacetime clearly provides

a stationary solution (recall that dp

/dt = 0). Jeans’ theorem is particularly useful in

constructing equilibrium solutions. Equilibrium solutions provide initial data for full scale

dynamical evolution simulations, which are necessary to determine the dynamical stability

of collisionless equilibria and the ﬁnal fate of unstable systems.

For spherical, static equilibrium systems, the general solution to the Liouville equation

depends on just two constants of the motion, the “energy at inﬁnity” E and the total

angular momentum J. Thus the distribution function has the form F = F(E, J, m). Adopt

a familiar Schwarzschild coordinate system (t, r,θ,φ) to describe the static spherical

spacetime, whereby the metric may be written as

=−e

2

+ e

2

(dθ

+ sin

θdφ

), (5.218)

where  and  are functions of r and the energy and angular momentum are given by

E =−p

, (5.219)

J =



sin



1/2

. (5.220)

Exercise 5.41 Show that E and J deﬁned in equations (5.219)and(5.220)are

constants of the motion in a static spherical spacetime.

These are the ﬁrst steps in the construction of a spherically symmetric equilibrium con-

ﬁguration. The dynamical equation for the matter, the Liouville equation, is automatically

solved given F = F(E, J, m). However the stress-energy tensor (5.206), as well as the