Bhushan B. Handbook of Micro/Nano Tribology, Second Edition
Подождите немного. Документ загружается.

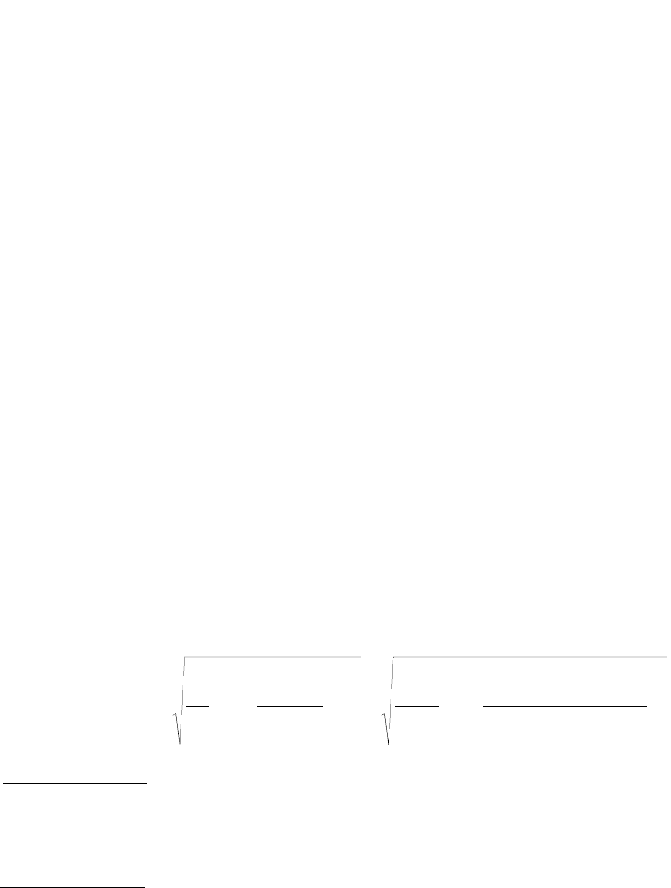
© 1999 by CRC Press LLC
found that the surface heights of a ground-glass surface were not symmetric like the normal distribution
but were best fitted by an ICS distribution with ν = 21.
4.3.2 RMS* Values and Scale Dependence
A rough surface is often assumed to be a statistically stationary random process
(Papoulis, 1965). This
means that the measured roughness sample is a true statistical representation of the entire rough surface.
Therefore, the probability distribution and the standard deviation of the measured roughness should
remain unchanged, except for fluctuations, if the sample size or the location on the surface is altered.
The properties derived from the distribution and the standard deviation are therefore unique to the
surface, thus justifying the use of such roughness characterization techniques.
Because of simplicity in calculation and its physical meaning as a reference height scale for a rough
surface, the rms height of the surface is used extensively in tribology. However, it was shown by Sayles
and Thomas (1978) that the variance of the height distribution is a function of the sample length and
in fact suggested that the variance varied as
(4.3.6)
where L is the length of the sample. This behavior implies that any length of the surface cannot fully
represent the surface in a statistical sense. This proposition was based on the fact that beyond a certain
length, L, the surface heights of the same surface were uncorrelated such that the sum of the variances
of two regions of lengths L
1
and L
2
can be added up as
(4.3.7)
They gathered roughness measurements of a wide range of surfaces to show that the surfaces follow the
nonstationary behavior of Equation 4.3.6. However, Berry and Hannay (1978) suggested that the variance
can be represented in a more general way as follows:
(4.3.8)
where n varies between 0 and 2.
If the exponent n in Equation 4.3.8 is not equal to zero of a particular surface, then the standard
deviation or the rms height, σ, is scale dependent, thus making a rough surface a nonstationary random
process. This basically arises from the multiscale structure of surface roughness where the probability
distribution of a small region of the surface may be different from that of the larger surface region as
depicted in Figure 4.4b. If the larger segment follows the normal distribution, then the magnified region
may or may not follow the same distribution. Even if it does follow the normal distribution, the rms σ
can still be different.
Other statistical parameters that are also used in tribology (Nayak, 1971, 1973) are the rms slope, σ′
x
,
and rms curvature, σ″
x
, defined as
(4.3.9)
*The rms values (of height, slope, or curvature) are related to the corresponding standard deviation, σ, of a surface
in the following way: rms
2
= σ
2
+ z
m
2
, where z
m
is the mean value. In this chapter it will be assumed that z
m
= 0; that
is, the mean is taken as the reference, such that rms = σ.
σ
2
≈ L
σσσ
2
12
2
1
2
2
LL L L+
()
=
()
+
()
σ
2
≈ L
n
′
=
∂
()
∂
=
−
()
−
()
∫
∑
+
=
−
σ
x
x
L
ij ij
ii
N
L
zx y
x
dx
N
zx y zx y
x
x
11
1
0
2
1
2
1
,,,
∆
© 1999 by CRC Press LLC
(4.3.10)
Here, although the rms slope and the rms curvature are expressed only for the x-direction, these values
can similarly be obtained for the y-direction. These parameters are extensively used in contact mechanics
(McCool, 1986) of rough surfaces.
The question that now remains to be answered is whether the rms parameters σ, σ′, and σ″ vary with
the statistical sample size or the instrument resolution. Figure 4.6 shows the rms data for a magnetic tape
surface (Bhushan et al., 1988; Majumdar et al., 1991). Along the ordinate is plotted the ratio of the rms
value at a magnification, β, to the rms value at magnification of unity. The magnification β = 1 corre-
sponds to an instrument resolution of 4 µm and scan size of 1024 × 1024 µm containing 256 × 256
roughness data points. The roughness data in the range 1 < β < 10 were obtained by optical interferometry
(Bhushan et al., 1988), whereas for β > 10, the data were obtained by atomic force microscopy (Majumdar
et al., 1991; Oden et al., 1992). An increase in β corresponds to an increase in instrument resolution with
the highest being equal to 1 nm. The data clearly show that the rms height does not change over five
decades of length scales and can therefore be considered scale independent over this range of length scales.
However, the rms slope increases with magnification as β
1
and the rms curvature increases as β
2
. Figure 4.7
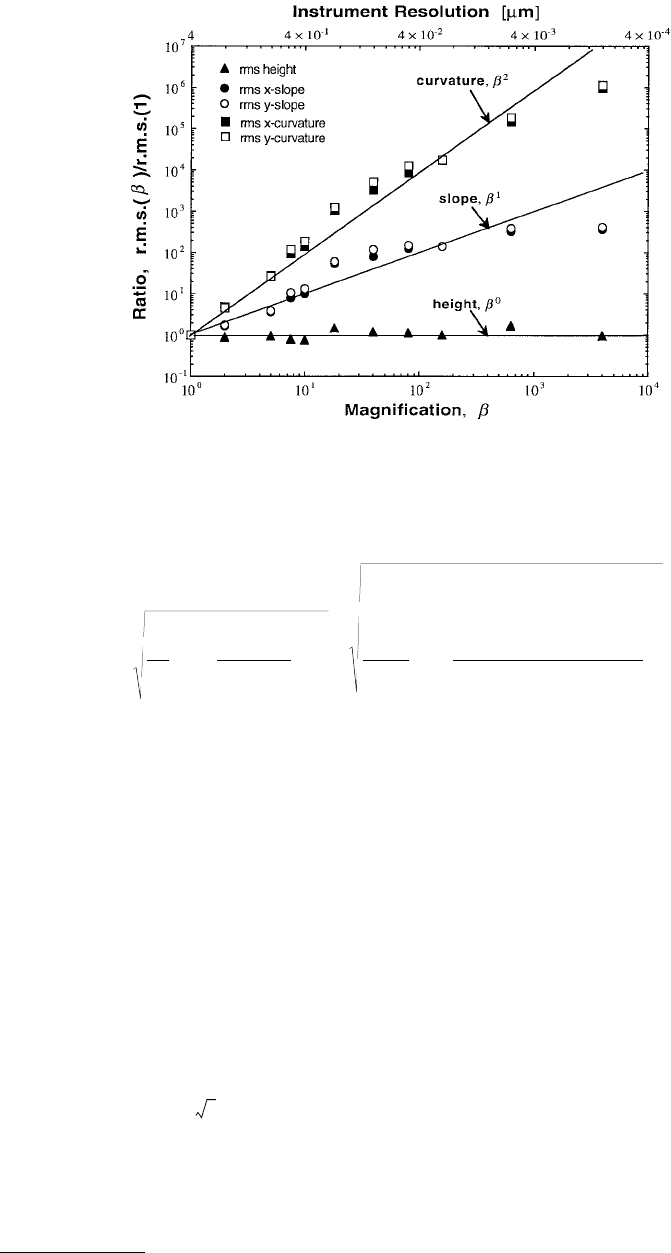
shows similar variations for a polished aluminum nitride surface where the roughness data was obtained
by atomic force microscopy. In this case, the rms height σ reduces with decreasing sample size but does
not follow the trend σ ≈ as suggested by Sayles and Thomas
(1978). Nevertheless, the variation does
make the surface a nonstationary random process. The rms slope and the rms curvature, on the other
hand, increase with the instrument resolution, as observed in Figure 4.7.
Although Figures 4.6 and 4.7 show statistics for specific surfaces, the trends are typical for most rough
surfaces that have been examined. The following can be concluded from these trends. The rms height,
FIGURE 4.6 Variation of rms height, slope, and curvature of a magnetic tape surface as a function of magnification,
β, or instrument resolution. The vertical axis is the ratio of an rms quantity at a magnification β to the rms quantity
at magnification of unit, which corresponds to an instrument resolution of 4 µm. Roughness measurements of β <
10 were obtained by optical interferometry (Bhushan et al., 1988), whereas that for β > 10 were obtained by atomic
force microscopy (Oden et al., 1992).
′′
=
∂
()
∂
=
−
()
+
()
−
()
∫
∑
+
+
=
−
σ
x
x
L
ij ij
ij
ii
N
L
zx y
x
dx
N
zx y zx y
zx y
x
x
11
2
2
2
2
0
2
2
1
2
2
,
,,
,
∆
L
© 1999 by CRC Press LLC
σ, is a parameter which could be scale independent for some surfaces but is not necessarily so for other
surfaces. The rms slope, σ′, and the rms curvature, σ″, on the other hand, always tend to be scale
dependent. Therefore, the rms height can be used to characterize a rough surface uniquely if it is scale
independent, as is the case of the magnetic tape surface in Figure 4.6. However, it is not clear under what
conditions the rms height is scale dependent or independent. These conditions will be explored in the
Section 4.3.3. However, the reasons can be qualitatively shown by the self-repeating nature of the surface
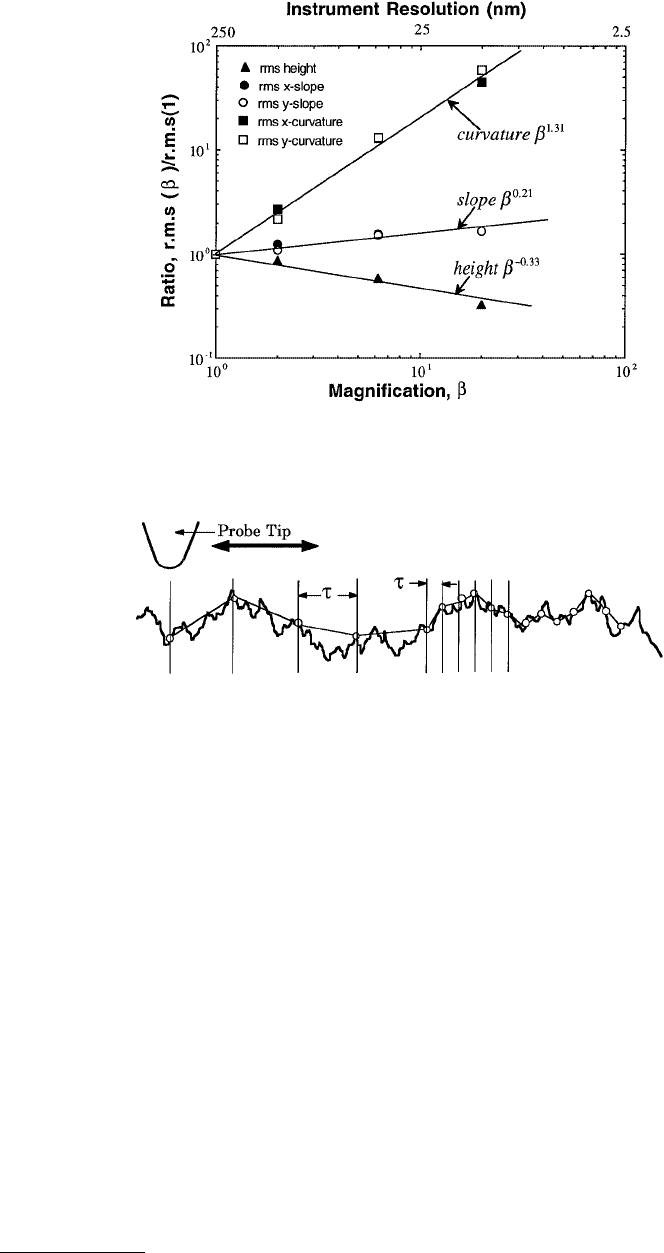
roughness depicted in Figure 4.8.
Given a rough surface, an instrument with resolution τ will measure the surface height of points that
are separated by a distance τ. If τ is reduced, new locations on the surface are accessed. Due to the multiple
scales of roughness present, a reduction in τ makes the measured profile look different for the same
surface. When τ is reduced, it is found that the straight line joining two neighboring points becomes
steeper on an average, as qualitatively observed in Figure 4.8. This increases the average slope and the
curvature of the surface. Therefore, the slope and the curvature fall victim to the “rough or smooth”
dilemma that is qualitatively discussed in Section 4.2. Figures 4.6 and 4.7 quantitatively exhibit scale
dependence of the rms slope and curvature. One can conclude these parameters cannot be used to
characterize a rough surface uniquely since they are scale dependent; that is, the use of these parameters
in any statistical theory of tribology can lead to erroneous results. It is thus necessary to obtain some
scale-independent techniques for roughness characterization.
FIGURE 4.7 Variation of rms height, slope, and curvature of a polished aluminum nitride surface as a function of
magnification, β, or instrument resolution.
FIGURE 4.8 Illustration of roughness measurements at different instrument resolution τ. As τ is reduced, the
surface that is measured is quite different, as qualitatively shown. The average slope and the average curvature of the
profile is higher for smaller τ.
© 1999 by CRC Press LLC
4.3.3 Fractal Techniques
4.3.3.1 A Primer for Fractals
The self-repeating nature of surface roughness has not only been found in surfaces but also in several
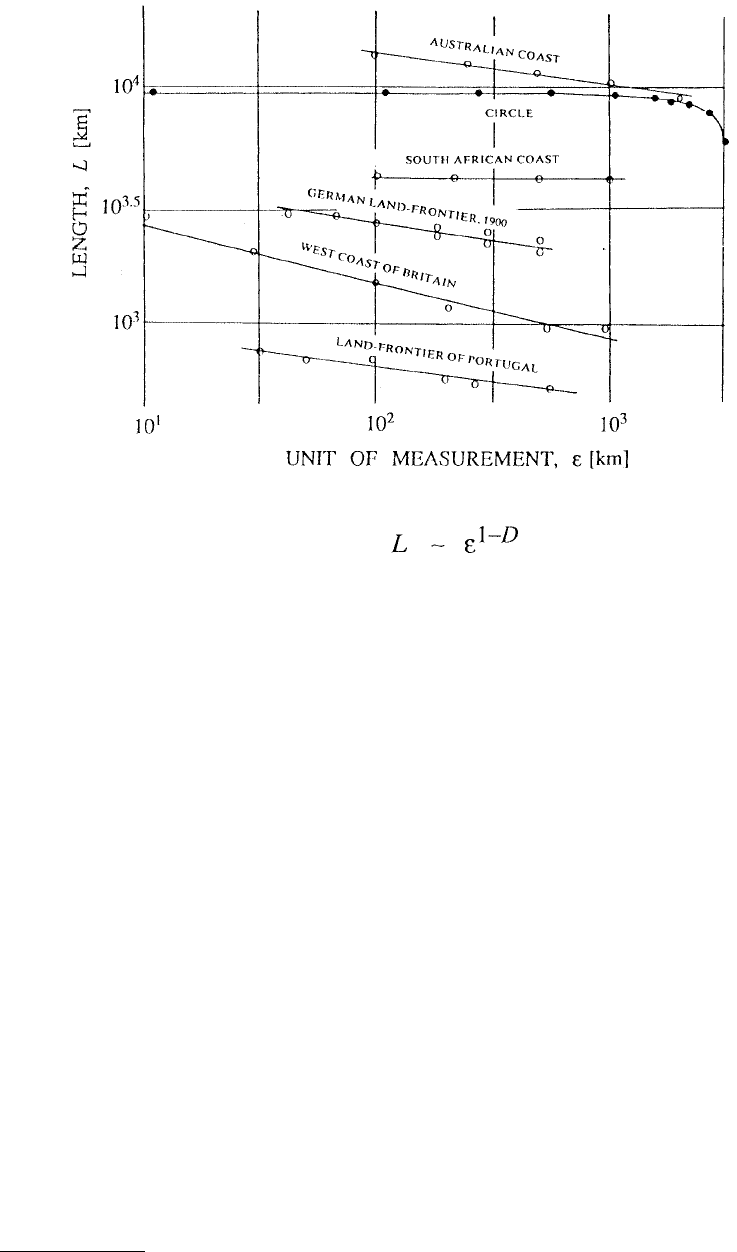
objects found in nature. In his classic paper, Mandelbrot (1967) showed that the coastline of Britain has
self-similar features such that the more the coastline is magnified, the more features and wiggliness are
observed. In fact, the answer to the question — “How long is the coastline of Britain?” — is it depends
on the unit of measurement and is not unique. This is shown in Figure 4.9 for several coastlines and also
for a circle. The fundamental problem of this scale dependence is that “length” as measured by a ruler
or a straightedge is a measure of only one-dimensional objects. No matter how small a unit you take for
the measurement, the length would still come out the same. In other words, if you take a straight line,
then the length would be the same whether you take 1 mm or 1 µm as the unit of measurement. The
reason for the scale independence at a very minute scale is that the line or the curve is made up of smooth
and straight line segments. However, if an object is never smooth no matter what length scale you choose,
then repeated magnifications will reveal different levels of wiggliness as shown in Figure 4.10. Large units
of measurement fail to measure the small wiggliness of the curve, whereas the small units of measurement
will measure them. In other words, different units of measurement will measure only some levels of the
wiggliness but not all levels. Thus, one would get a different number for the length of the object as the
unit of measurement is changed.
Since objects of the dimension unity are defined to have their lengths independent of the unit of
measurement, an object with scale-dependent length is not one-dimensional. Similarly, if the area of a
surface depends on the unit of measurement, then it is not a two-dimensional object.
FIGURE 4.9 Dependence of the length of different coastlines and curves on the unit ε of measurement. Note the
power law dependence of the length on ε.

© 1999 by CRC Press LLC
One of the properties of naturally occurring wiggly objects is that if a small part of the object is
enlarged sufficiently, then statistically it appears very similar to the whole object. For example, if you
look at the photograph of hills and valleys (with appropriate color), then unless the scale is given it will
be very difficult to say whether it is a photograph of the Rocky Mountains or a micrograph of a surface
obtained by a scanning electron microscope. This feature is called “self-similarity.” To characterize such
wiggly and complex objects which display self-similarity, Mandelbrot (1967) generalized the definition
of dimension to take fractional values such that a wiggly curve like the coastline will have a dimension D
between 1 and 2. Under such a generalized definition, the specific integer values of 0, 1, 2, and 3
correspond to smooth objects such as a point, line, surface, and sphere (or any three-dimensional object),
whereas the generalized noninteger values correspond to wiggly and complex objects which show self-
similar behavior. Self-similar objects that contain nonsmooth self-similar features over all length scales
are called fractals and the noninteger dimension characterizing it is called the fractal dimension. Detailed
discussions on fractal geometry can be found in several books
(Mandelbrot, 1982; Peitgen and Saupe,
1988; Barnsley, 1988; Feder, 1988; Vicsek, 1989; Avnir, 1989).
A rough surface, as shown in Figure 4.1, has fractallike features — it has wiggly features appearing
over a large range of length scales and, as will be shown later, they sometimes do follow the self-similar
hierarchy. Whereas mathematical fractals follow self-repetition over all length scales, rough surfaces have
a higher and lower length scale limit between which the fractal behavior is observed. Analogous to the
nonuniqueness of the length of a coastline, we have already seen the nonuniqueness of the rms height,
the rms slope, and the rms curvature. The question that a reader can ask is, can the fractallike behavior
of a rough surface be utilized to develop a characterization technique that will be independent of length
scales? Recent work (Kardar et al., 1986; Gagnepain, 1986; Jordan et al., 1986; Meakin, 1987; Voss, 1988;
Majumdar and Tien, 1990; Majumdar and Bhushan, 1990) has shown that this is sometimes possible
and is discussed below.
Figure 4.9 shows that if the length, L, of a coastline is plotted against the unit of measurement, ε, then
the length follows a power law of the form (Mandelbrot, 1967)
(4.3.11)
FIGURE 4.10 Repeated magnification of a coastline produces an
increased amount of wiggliness without any appearance of smoothness
at any scale. Note that the magnification is equal in all directions.
L
D
≈
−
ε
1

© 1999 by CRC Press LLC
where D is called the fractal dimension of the coastline. If D = 1, then the length is independent of ε and
it can be called a one-dimensional object. It is observed that this power law behavior remains unchanged
over several decades of length scales such that the value of D, which in some sense measures the wiggliness
of the curve, remains constant and independent of ε. Therefore, D is one parameter that can be used to
characterize a coastline. Another way of looking at this behavior is the following — although the coastline
seems a rather convoluted and complex geometric structure, the power law behavior represents a pattern
or order in this chaotic structure.
4.3.3.2 Fractal Characterization of Surface Roughness
The same concept can be used to characterize a rough surface. However, there is a difference between a
coastline and a rough surface. To show the self-similarity of a coastline, one needs to take a small part
and enlarge it equally in all directions to resemble the full coastline statistically, as qualitatively shown
in Figure 4.9. However, for a small region of a rough surface to statistically resemble* a larger region, the
enlargement should be done unequally in the vertical (z) and lateral (x and y) directions. Such objects,
which scale differently in different directions, are called self-affine (Mandelbrot, 1982, 1985; Voss, 1988).
To characterize a self-affine object one cannot use the length of the surface profile or the area of the
surface as a measure
(Mandelbrot, 1985). There are two other ways to characterize it — the power
spectrum P(ω) and the structure function, S(τ).
4.3.3.2.1 Power Spectrum
Consider a surface profile, z(x) in the x-direction. The power spectrum of the profile can be found by
the relation (Blackman and Tuckey, 1958; Papoulis, 1965):
(4.3.12)
where the coordinate x ranges from 0 to L. The power spectrum can be obtained from a measured
roughness profile by a simple fast Fourier transform routine
(Press et al., 1992). The square of the
amplitude of z(x) or the power at a frequency ω is equal to P(ω)dω. The rms height, the rms slope, and
the rms curvature can be obtained from the power spectrum (McCool, 1987; Majumdar and Bhushan,
1990):
(4.3.13)
(4.3.14)
(4.3.15)
where ω
l
and ω
h
are the low-frequency and the high-frequency cutoffs, respectively. For a roughness
measurement, the low-frequency cutoff is equal to the reciprocal of the sample length, ω
l
= 1/L and the
high-frequency cutoff is equal to the Nyquist frequency or equal to ω
h
= ½τ, where τ is the distance
between two adjacent points of the data sample. It is evident that the power spectrum is a more
*Statistical resemblance is for the power spectrum or structure function of the rough surface as shown later.
P
L
zx i x dx
L
ωω
()
=
() ( )
∫
1
0
2
exp
σωω
ω
ω
=
()
∫
Pd
l
h
′
=
()
∫
σωωω
ω
ω
2
Pd
l
h
′′
=
()
∫
σωωω
ω
ω
4
Pd
l
h
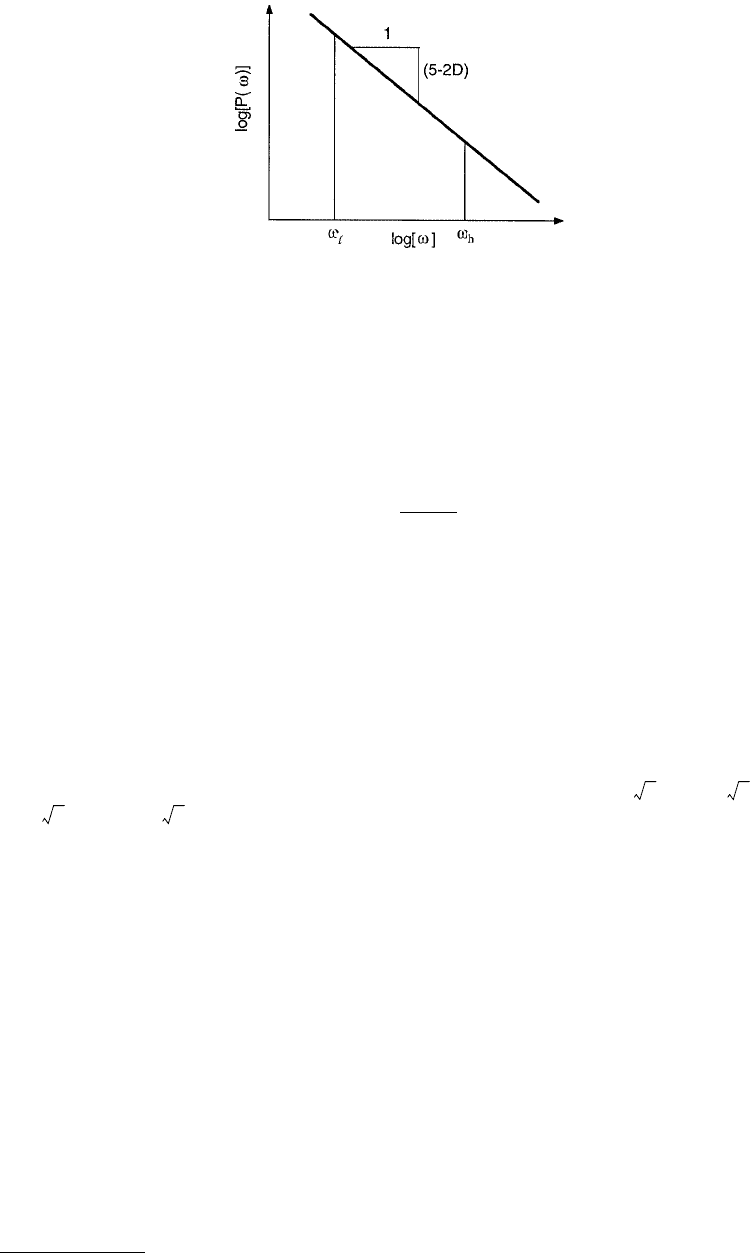
© 1999 by CRC Press LLC
fundamental quantity than the rms values since the rms values can be obtained from the spectrum, and
not vice versa.
For a fractal surface profile, the power spectrum follows a power law of the form (Mandelbrot, 1982;
Voss, 1988; Majumdar and Tien, 1990; Majumdar and Bhushan, 1990):
(4.3.16)
where 1 < D < 2 is the fractal dimension of the profile and C is a scaling constant, which depends on
the amplitude of the rough surface. If the power spectrum of a measured surface profile is found and
plotted against the frequency in a log–log plot, then the surface profile can be called fractal if the spectrum
follows a straight line, as qualitatively shown in Figure 4.11. The dimension D can be obtained from the
slope and the constant C from the power. Since the profile is a vertical cut through a surface, the dimension
of the surface, D
s
is equal D
s
= D + 1 only for an isotropic surface. For anisotropic surfaces one needs to
determine the fractal dimensions of surface profiles in different directions. For a fractal profile, the
independence of D and C from the length scale ω make them unique to a surface and can therefore be
used for roughness characterization. When the rms quantities are obtained from the fractal spectrum by
using Equations 4.3.13 through 4.3.15), they exhibit the following behavior: σ = ω
l
–(2–D)
= L
(2–D)
;
σ′ = ω
h
(D–1)
; σ″ = ω
h
D
. It is evident that the rms values depend either on the low-frequency or high-
frequency cutoff and are therefore scale dependent. Figures 4.6 and 4.7 confirm this experimentally and,
in fact, show the decrease in exponent by 1 as we go from the rms curvature to the rms slope and finally
to the rms height. The only difference that one finds in the rms quantities is that the rms slope and the
curvature depend on the high-frequency cutoff, whereas the rms height depends on the low-frequency
cutoff. The relation σ ≈ L
(2-D)
is exactly the same as suggested in Equation 4.3.8 with n = 2(2 – D). In
fact, the relation suggested by Sayles and Thomas (1978) in Equation 4.3.6 is a special case when D = 1.5.
The variance of the height distribution, σ
2
, is equal to the area under the power spectral curve as
mathematically shown in Equation 4.3.13. When the variance (or the rms height) is independent of the
sample size or any length scale, as demonstrated in Figure 4.6, the area under the power spectrum must
be constant and independent of ω
l
and ω
h
. Therefore, the fractal power law variation of the spectrum in
Equation 4.3.16 is clearly not valid for such a case since it always leads to ω
l
-dependence of the rms
height. One must note, then, that the fractal behavior is not followed all the time.
One of the practical difficulties of using the power spectrum to obtain the values of D and C is that
for a single measured roughness profile, the calculated spectrum turns out to be very noisy. This is because
the roughness profile is not bandwidth limited and is in fact a broad-band spectrum. However, the power
spectrum of any measured roughness will be limited to the Nyquist frequency ω
n
, on the high-frequency
FIGURE 4.11 Qualitative description of a fractal power spectrum plotted on a log–log plot. Note that the spectrum
is a straight line whose slope depends on the fractal dimension. A roughness measurement contains a lower, l, and
upper limit, L, of length scales which correspond to the frequency window between ω
l
= 1/L and ω
h
= 1/(2l).
P
C
D
ω
ω
()
=
−
()
52
C C
C C

© 1999 by CRC Press LLC
side. This gives rise to the problem of aliasing
(Press et al., 1992) which falsely translates the power of
frequencies in the range ω > ω
n
into the range ω < ω
n
. The problem comes about due to the discreteness
of the roughness measurement. To overcome this problem, we have found that the structure function
can yield more accurate estimation of D and C.
4.3.3.2.2 Structure Function
The structure function (Mandelbrot, 1982; Voss, 1988) is defined as
(4.3.17)
The summation on the right-hand side can be used for calculation of a measured surface profile con-
taining N points. As one can see, the structure function is easy to calculate since it does not involve any
transformation but simple height differences and averages. It is sometimes used in experimental and
theoretical analysis of velocity and scalar fluctuations in turbulent fluid dynamics
(Kolmogoroff, 1941).
In turbulence, the fluctuating quantity varies with time and space, whereas for rough surface, the same
varies with space. The problems are quite similar since in turbulence, too, the power spectrum of the
fluctuations is broadband and follows the power law behavior of Equation 4.3.16.
It is interesting to note that in some ways the structure function and the variance, σ
2
, of height in
Equation 4.3.4 are similar since both involve finding the average of the square of height differences.
However, the structure function uses height differences with points separated by a distance τ, whereas
for the variance, the height differences are with the mean height z
m
. The structure function yields much
more information than the rms height since by varying τ, one can study the roughness structure at
different length scales. This is, of course, not possible for the variance, σ
2
, which finds the average height
difference from the mean over the whole surface. In addition, the variance of the profile slope, S′(τ), can
be found as
(4.3.18)
A surface profile is said to be fractal if the structure function follows a power law behavior
as (Man-
delbrot, 1985; Voss, 1988; Majumdar et al., 1991)
(4.3.19)
This can also be derived from the power spectrum by the relation (Berry, 1978)
(4.3.20)
where D is the fractal dimension and G is a scaling constant that has units of length. When S(τ) is plotted
against τ on a log–log plot, the curve will be a straight line for a fractal profile. The dimension can be
obtained from the slope and G from the intercept at a certain value of τ. The two characterization
parameters, D and G, are unique for a fractal profile and are independent of any length scale τ. Thus,
they form the fundamental set of parameters for a rough surface profile. By using the fractal power law
spectrum of Equation 4.3.16 in Equation 4.3.20, the structure function becomes
(Berry, 1978)
S
L
zx zx dx
Nx
zx zx
L
ii
i
Nx
ττ
τ
τ
τ
()
=+
()
−
()
[]
=
−
()
+
()
−
()
[]
∫
∑
=
−
()
11
2
0
2
1
∆
∆
′
()
=
+
()
−
()
=
()
∫
S
L
zx zx
dx
S
L
τ
τ
τ
τ
τ
1
2
0
2
SG
DD
ττ
()
=
−
()
−
()
2122
SPidτ ω ωτ ω
()
=
() ( )
−
[]
−∞
∞
∫
exp 1

© 1999 by CRC Press LLC
(4.3.21)
such that the factor C of the power spectrum is related to the scaling constant G of the structure function as
(4.3.22)
Berry and Blackwell (1981) follow a slightly different definition of a fractal surface — a surface profile
is said to be a self-affine fractal when
(4.3.23)
where the parameter G is called “topothesy” following the term coined by Sayles and Thomas
(1978).
This definition is valid in the limit τ→0 and the fractal dimension D so obtained is called the Haus-
dorff–Besicovitch dimension
(Mandelbrot, 1982). For larger-scale roughness, Berry and Blackwell (1981)
suggest a simple model for S(τ) as
(4.3.24)
As τ→0, Equation 4.3.24 is recovered and when τ G(2σ/G)
1/(2–D)
, S(τ) = 2σ
2
. In this case it is assumed
that the rms height, σ, is independent of the sample size and can be obtained from roughness data for
a sample size larger than the correlation length, τ
c
= G(2σ/G)
1/(2–D)
. Experimental data will show that the
behavior of Equation 4.3.24 is followed by several surfaces and can be used as a good model for surfaces.
However, if the rms height is scale dependent, as observed by Sayles and Thomas
(1978), then the model
breaks down.
In the rest of the chapter the structure function will be used to study the statistical properties of rough
surfaces. This is due to its simplicity of use and the roughness information it reveals at different length
scales.
4.3.3.3 Roughness Measurements
Typically, roughness between 1 cm to about 10 µm is measured by stylus profilometers, between 500 and
1 µm by optical interferometry and between 100 µm and 1 Å by scanning tunneling or atomic force
microscopy. The overlaps in the length scales between these instruments are used to corroborate the
roughness measured by different techniques.
4.3.3.3.1 Stylus Profilometry
The roughness of machined (lapped, ground, and shape turned) stainless steel surfaces was measured by
a contact stylus profiler
(Majumdar and Tien, 1990). The instrument used a diamond stylus of radius
2.5 µm and had a vertical resolution of 0.5 nm. The scan lengths ranged from 50 to 30 mm with each
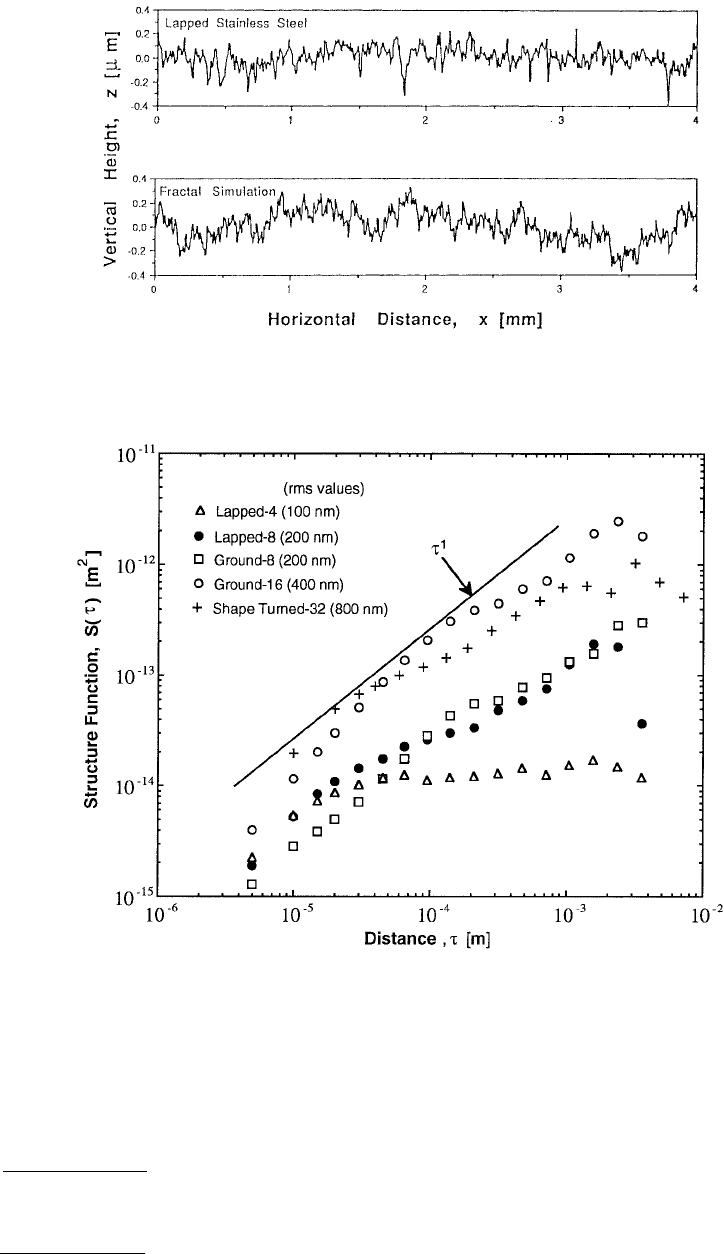
scan having 800 to 1000 evenly spaced points. Figure 4.12 shows the roughness profile of a lapped stainless
steel surface.
The structure functions, S(τ), of these surface profiles are plotted on a log–log plot in Figure 4.13.
Also shown is the straight line, S(τ) ≈ τ
1
, which corresponds to a fractal dimension of D = 1.5. It is
S
C
D
D
D
D
ττ
()
=
−
()
π−
()
−
()
−
()
2
23
2
23
22
sin Γ
C
DG
D
D
D
=
−
()
π−
()
−
()
−
()
2
23
2
23
21
sin Γ
SG
DD
ττ τ
()
=→
−
()
−
()
2122
0 for
S
G
DD
τσ
τ
σ
()
=−−
−
()
−
()
21
2
2
2122
2
exp
© 1999 by CRC Press LLC
evident that the experimental structure functions do follow a power law at small length scales. In fact,
although they do not coincide, they all tend to follow the same slope, that of D = 1.5. The higher value
of S(τ) for the rougher surfaces leads to a higher value of G. The structure function for the lapped-4*
FIGURE 4.12 Profile of lapped stainless steel surface measured by a stylus profilometer. Fractal simulation of the
profile was conducted by the Weierstrass–Mandelbrot function. (From Majumdar, A. and Tien, C. L. (1990), Wear
136; 313–327. With permission.)
FIGURE 4.13 Structure function of machined stainless steel surfaces whose roughness was measured by stylus
profilometry.
*The number associated with each process is the rms roughness produced in microinches. One microinch is equal
to 25.4 nm.
