Bhushan B. Handbook of Micro/Nano Tribology, Second Edition
Подождите немного. Документ загружается.

© 1999 by CRC Press LLC
of V(l) and K(l) will be used. There is no need to prove whether the surface is fractal or nonfractal. If
the surface is fractal, both these parameters will show scaling behavior. If the surface is nonfractal and
yet contains multiple length scales, this technique will allow one to incorporate the scale-dependent
information contained in V(l) and K(l). When the surface is perfectly periodic with wavelength, λ, then
K(l) will show a peak when l = λ/2. In general, V(l) and K(l) neither follow scaling behavior nor do
they show sudden jumps in the data but are a combination of both. It will be shown in Section 4.5 that
these characteristics can be used to develop theories of contact mechanics and other tribological phe-
nomena. Before that, it is necessary to understand how this technique can be used to characterize
anisotropic surfaces.
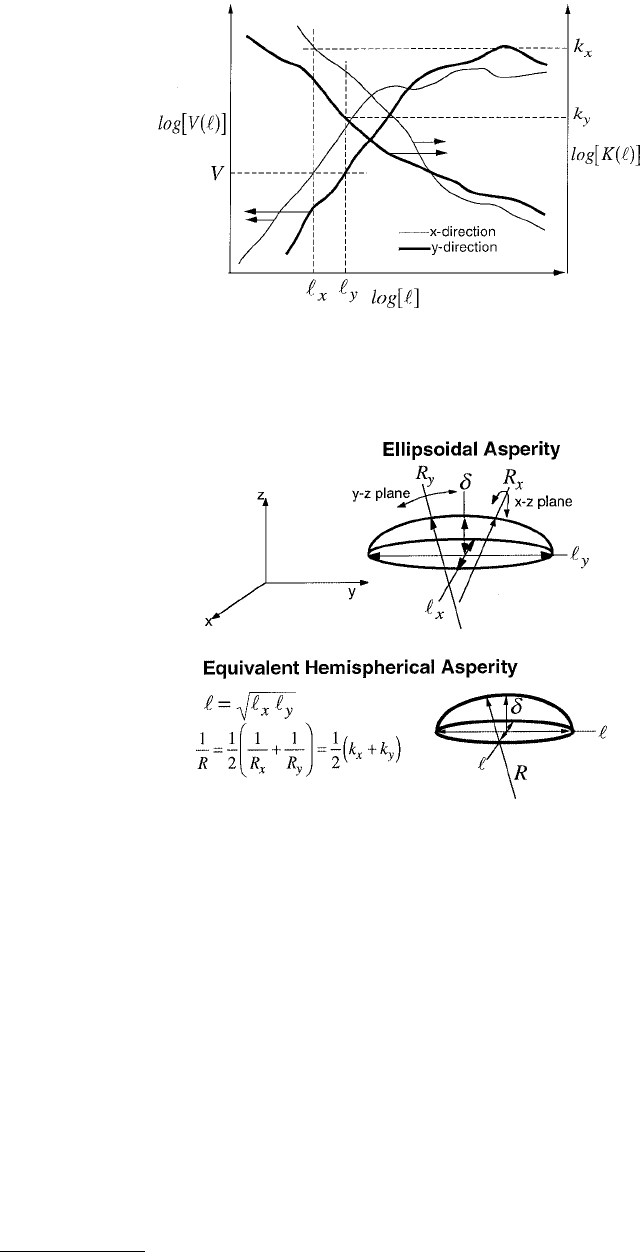
Consider a typical plot of V
x
, V
y
, K
x
, and K
y
as a function of l for a general anisotropic surface in
Figure 4.25. An asperity on this surface will have an elliptic base with major and minor axes l
x
and l
y
and curvatures k
x
and k
y
as shown in Figure 4.26. The values of l
x
and l
y
can be found from Figure 4.25
by taking the intersection of a horizontal line with the V
x
and V
y
curves. Intersections of the vertical lines
through l
x
and l
y
with the K
x
and K
y
curves give the respective curvature values of k
x
and k
y
. Note that
it is possible to have more than one intersection of a horizontal line with the curves V
x
and V
y
producing
FIGURE 4.25 Qualitative demonstration of a typical V vs. l and K vs. l plot for the generalized roughness
characterization technique. Note that, in general, the surface is anisotropic such that the curves are different in the
x- and y-directions.
FIGURE 4.26 (a) Schematic diagram of an ellipsoidal asperity of an anistropic surface. (b) Equivalent hemispherical
asperity that can be used to study the mechanics of contact with a flat hard plane.
© 1999 by CRC Press LLC
more than one value of l
x
and l
y
, as shown in Figure 4.25. The area of an asperity base is a = πl
x
l
y
. For
more than one value of l
x
and l
y
, the product l
x
l
y
can be obtained for different combinations, and
therefore for a particular value of V = constant (horizontal line) it is possible to have different asperity
base areas. For each combination of l
x
l
y
, the effective curvature of an ellipsoidal asperity of base area a
is k(a) = 0.5(k
x
+ k
y
). This will be used in the contact mechanics of ellipsoidal asperities (Timoshenko
and Goodier, 1970) with a flat plate. The procedure followed above collapses the anisotropic roughness
data in the x- and y-directions in Figure 4.25 into a plot of V and k vs. the asperity base area a.
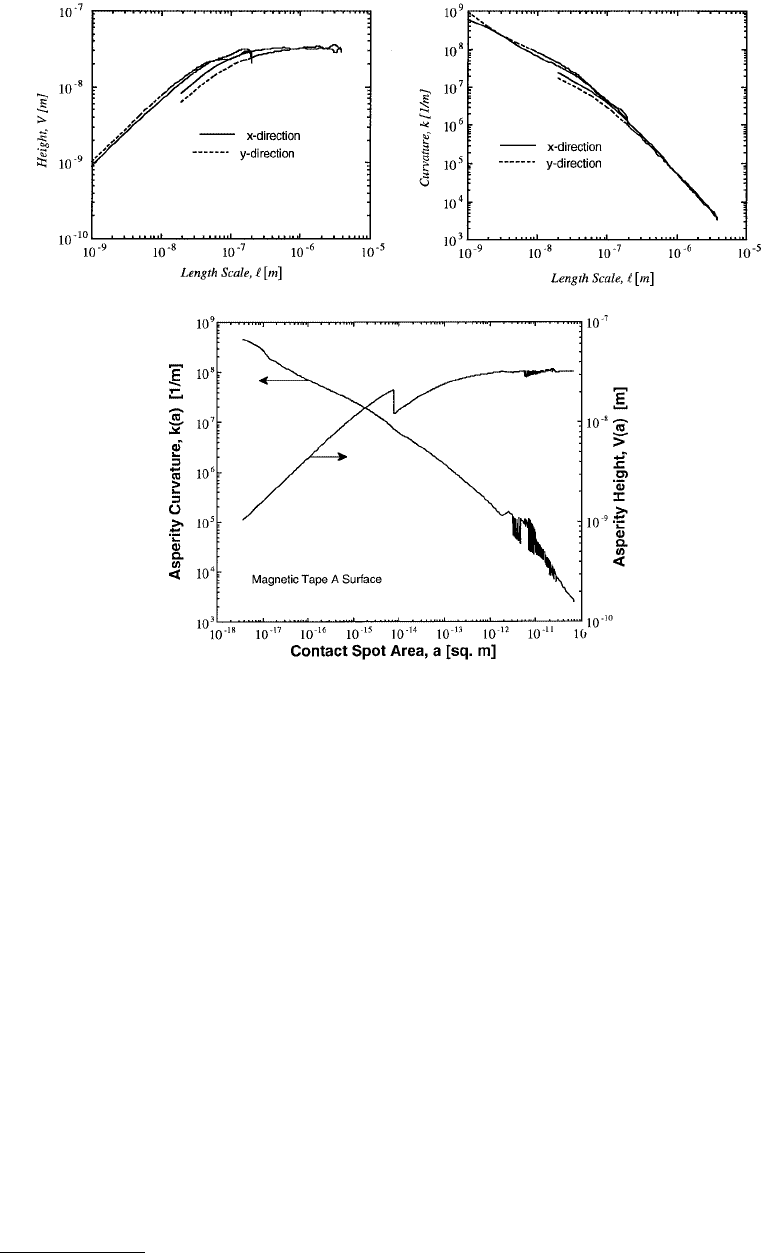
Roughness data of a magnetic tape surface will be taken as an example to demonstrate the application
of the generalized contact mechanics model. Figure 4.27a shows the plots of V
x
, V
y
, K
x
, and K
y
as a function
of l for a magnetic tape, whereas Figure 4.27b shows the collapsed data of V(a) and K(a) as a function
of asperity base area, a. The roughness was measured by an atomic force microscope and the details of
the measurement as well as the surface images are described elsewhere
(Oden et al., 1992).
It is evident that this generalized roughness characterization technique does not demand any require-
ments for either a scaling fractal surface structure or a surface with single scale of asperities. In that
respect, it is more powerful than the other techniques, as will be shown in Section 4.5. However, the
simplicity of the rms characterization or the fractal techniques that use only G and D is more than that
of the generalized technique. As will be shown later, numerical integration must be performed to get any
meaningful results for contact mechanics and size distribution.
FIGURE 4.27 Variation of surface height V and curvature K for the magnetic tape A surface. (a) V and K vs. l for
two orthogonal directions; (b) V and K vs. the asperity base area. This collapses the curves in (a) by the procedure
discussed in the text.

© 1999 by CRC Press LLC
4.4 Size Distribution of Contact Spots
As discussed in Section 4.2, our goal in characterizing rough surfaces is to determine the size and spatial
distribution of contact spots due to asperity–asperity contact. Conventional methods in tribology (Bhus-
han, 1990) use an asperity density, η, as a measure of number of spots per unit area and a mean diameter,
–
d, as a measure of the average spot size. Although η counts the number, it does not involve the size
distribution which may be useful for scale-dependent tribological phenomena. In addition, the asperity
density under elastic contact theory is found by its statistical relationship to the rms height and the
curvature as (Bhushan, 1984a,b)
(4.4.1)
(4.4.2)
where F is the normal load, E is the elastic modulus, and A
a
is the apparent area. As has been proved
earlier, the rms parameters are not unique for a surface. Therefore, any estimate of the asperity density
using these parameters is also not unique.
4.4.1 Observations of Size Distribution for Fractal Surfaces
The multiscale nature of surface roughness suggests that there will be spots of different sizes. As can be
observed in Figure 4.3, which is a simulation of a real surface contact, the spots come in all sizes and
shapes. As a general trend it is evident that there is a greater number of smaller spots than larger ones.
Consider first a fractal surface of profile dimension D and surface dimension D + 1. In the study of
geomorphology of Earth, Mandelbrot (1975) found that the cumulative size distribution of islands on
Earth’s surface follows the power law N(a) ≈ a
–D/2
, where N is the total number of islands with area larger
than a and D is the fractal dimension of the coastline of the islands. The coastline is a self-similar curve
for which the dimension D is related to the surface dimension D
s
by the relation D = D
s
– 1. If the surface
of, for example, a machined metal or a thin-film magnetic disk is enlarged enough, the hills and valleys
would appear similar to that found on Earth’s surface. The contact spots formed by a horizontal cut of
such a surface by a contact plane would be analogous to the islands formed by cutting the Earth’s surface
by that of the ocean. Therefore, it can be expected that the contact spots would also follow a power law
relation of the form:
(4.4.3)
where the distribution is normalized by the area of the largest contact spot a
L
. The size distribution of
contact, n(a), is defined such that the number of contact spots between a and a + da is equal to n(a)da.
For a fractal surface, the distribution n(a) can be obtained from N(a) of Equation 4.4.3 as
(4.4.4)
η
σ
σσσ
≈
′′
()
′′
FEA
a
d ≈
′′
σ
σ
Na
a
a
L
D
()
=
2
na
dN
da
D
a
a
a
L
D
()
=− =
2
2
© 1999 by CRC Press LLC
If any instrument is used to count the number of spots and measure their diameters, the values would
obviously be finite and nonzero, respectively. Therefore, conventional parameters such as the contact
spot density η and the mean diameter
–
d can be used to quantify the size distribution of contact spots.
However, note that in the distribution of Equation 4.4.3 the number of the largest spot is unity, whereas
the number of spots of area a → 0
would tend to infinity. There is obviously a discrepancy between the
two methods. One must note that since any measuring instrument is limited by its resolution, not all
spots on the contact interface can be detected. In other words, both η and the mean spot diameter are
instrument-dependent parameters as has been analytically shown
(Majumdar and Bhushan, 1990). The
fractal model does not involve these parameters and allows the smallest spot area to tend to zero with
their number tending to infinity.
4.4.2 Derivation of Size Distribution for Any Surface
The power law behavior of Equation 4.4.4 is not only an experimental observation, but can be proved
rigorously as follows. Consider a rough surface to contact a hard flat plane such that the surface mean
and the plane is separated by a distance, d. Then the real area of contact, A
r
, can be written in two ways:
(4.4.5)
The first integral is the summation over all the contact spots where a
L
is the area of the largest contact
spot. The second integral is over the probability distribution g(z) of the surface heights as described in
Section 4.3.1, where A
a
is the apparent surface area. The size distribution n(a) can, hence, be found as
(4.4.6)
where the chain rule is used for the right-hand side.
Now dA
r
/dz is related to g(z) as
(4.4.7)
The factor dz/da must be derived from the deformation of a single asperity. Consider an asperity of
curvature k(a) in contact with a flat hard plane such that the contact area is equal to a and the deformation
is equal to δ. Since δ increases in the negative z-direction, dz/da = -dδ/da.
4.4.2.1 Size Distribution under Elastic Deformation
If the contact is under elastic deformation, then according to Hertzian theory
(Timoshenko and Goodier,
1970; Johnson, 1985) the asperity deformation δ is related to the area a of contact and curvature k as
(4.4.8)
such that dz/da is equal to
(4.4.9)
A n a a da A g z dz
r
a
a
d
L
=
()
=
()
∫∫
∞
0
na
a
dA
da a
dA
dz
dz
da
rr
()
==
11
dA
dz
Agd
r
zd
a
=
=−
()
δ=
()
π
ak a
dz
da
ka
a
ka
dk
da
=−
()
π
+
()
1

© 1999 by CRC Press LLC
Combining this with dA
r
/dz, the size distribution n
e
(a) can be written as
(4.4.10)
This is an important result, because the only assumption that has been made in deriving this result is
that the asperity has an ellipsoidal shape of an effective curvature k(a). It is a general relation for any
surface — fractal or nonfractal. If the surface deformations are predominantly elastic, then the largest
contact spot area, a
L
, can be found by using Equation 4.4.10 in the equality of Equation 4.4.5 to get
(4.4.11)
where Ω(d) is the cumulative probability distribution defined as
(4.4.12)
To use the size distribution, n
e
(a), of Equation 4.4.10 in any tribological analysis, it is necessary to find
the probability distribution, g(z), and the curvature, k(a), as a function of spot area a, and the separation
d between the two surfaces. The probability distribution, g(z), can be assumed to be a Gaussian or perhaps
some nonsymmetric function. The curvature, k(a), can be obtained by the generalized roughness char-
acterization technique discussed in Section 4.3.4. The separation, d, can be found by studying the contact
mechanics which depends on the applied normal load on the surface, the size distribution, n
e
(a), the
surface roughness, and the material properties such as hardness and elastic modulus. This will be dealt
with in Section 4.5.
4.4.2.1.1 Gaussian Height Distribution
If the surface heights have a Gaussian distribution, then the size distribution reduces to
(4.4.13)
where σ is the standard deviation of the surface heights. The largest contact spot area, a
L
, can be found
from Equation 4.4.12 to be
(4.4.14)
where erfc( ) is the complementary error function. Thus one would get a relation between a
L
and the
nondimensional height d/σ.
4.4.2.1.2 Fractal Surface
If the surface is a fractal with a profile dimension of D, then we saw earlier that the radius of curvature,
R, behaved as R = a
D/2
/G
D–1
such that k(a) = G
D–1
/a
D/2
. Therefore the size distribution, n
e
(a), varies with
spot size as
na
Akagd
a
a
ka
dk
da
e
a
()
=
()()
π
+
()
1
ka
a
ka
dk
da
da
d
gd
a
L
()
+
()
=
π
()
()
∫
1
0
Ω
Ω dgzdz
d
()
=
()
∞
∫
na
Aka
a
a
ka
dk
da
e
e
a
d
()
=
()
π
+
()
π
−
1
2
22
2σ
σ
ka
a
ka
dk
da
da
d
e
a
d
L
()
+
()
=π
π
⋅
()
∫
−
1
2
2
0
2
22
σσ
σ
erfc

© 1999 by CRC Press LLC
(4.4.15)
It is evident that the variation of n
e
(a) ≈ a
–(1+D/2)
is exactly what was observed by Mandelbrot
(1975) for
the distribution of islands on Earth’s surface and given in Equation 4.4.4. This is a mathematical derivation
of the experimentally observed distribution.
The largest island size, a
L
, can be found for a Gaussian fractal surface by using the relation k(a) =
G
D–1
/a
D/2
in Equation 4.4.14 to get the relation
(4.4.16)
Using the fact that , we find that
(4.4.17)
4.4.2.2 Size Distribution under Plastic Deformation
When the contact is under plastic deformation, then using volume conservation the area of contact is
found to follow (Chang et al., 1987):
(4.4.18)
where δ
c
(a) is the critical deformation such that when δ > δ
c
, the deformation is plastic and when δ <
δ
c
the deformation is elastic. It is clear that when δ = δ
c
, the relation for elastic deformation in
Equation 4.4.8 is retrieved. In this case, dz/da is equal to
(4.4.19)
More will be discussed on the critical deformation δ
c
in the section on contact mechanics whereas now
it will be stated that it depends on the contact area a and curvature as δ
c
= φ/k(a), where φ depends on
the material properties. By using this, the size distribution under plastic deformation is
(4.4.20)
For a Gaussian height distribution, one can follow the analysis for elastic deformation to obtain the
relation for the largest island. For a fractal surface with profile dimension, D, such that k(a) = G
D–1
/a
D/2
,
the size distribution can be shown to follow the relation:
na
AG gd
a
D
e
a
D
D
()
=
()
π
−
−
()
()
+
1
21
2
2
a
G
d
e
L
D
D
d
22
1
2
2
2
22
−
()
−
()
−
=π
π
()
σ
σ
σ
erfc
σ=
−−
()()
()
GL D
DD12
2Ψ
aL
D
d
e
L
d
D
=
ππ
()
−
−
()
2
2
22
2
2
22
Ψ
erfc σ
σ
δ
δ
=
()
+
()
π
c
aaka
22
dz
da
d
da
ka a
ka
dk
da
c
=− +
()
π
+
()
1
2
1
δ
na
Aka g d
a
k
dk
da
a
k
dk
da
p
a
()
=
()()
π
−
π
++
φ
2
1
2
1
3
© 1999 by CRC Press LLC
(4.4.21)
4.4.2.3 Size Distribution under Elastic-Plastic Deformations
In the next section it will be shown that when surface contact involves a combination of elastic and plastic
deformations there exists a critical contact spot area, a
c
, such that all spots smaller than the critical area,
a < a
c
, deform plastically and all spots larger than a
c
, a > a
c
, deform elastically. Under these circumstances,
the largest contact spot area, a
L
, must be found by the equation:
(4.4.22)
where n
e
(a) and n
p
(a) are given by Equations 4.4.10 and 4.4.20, respectively. If the surface is assumed to
have a Gaussian surface height distribution, Equation 4.4.22 reduces to
(4.4.23)
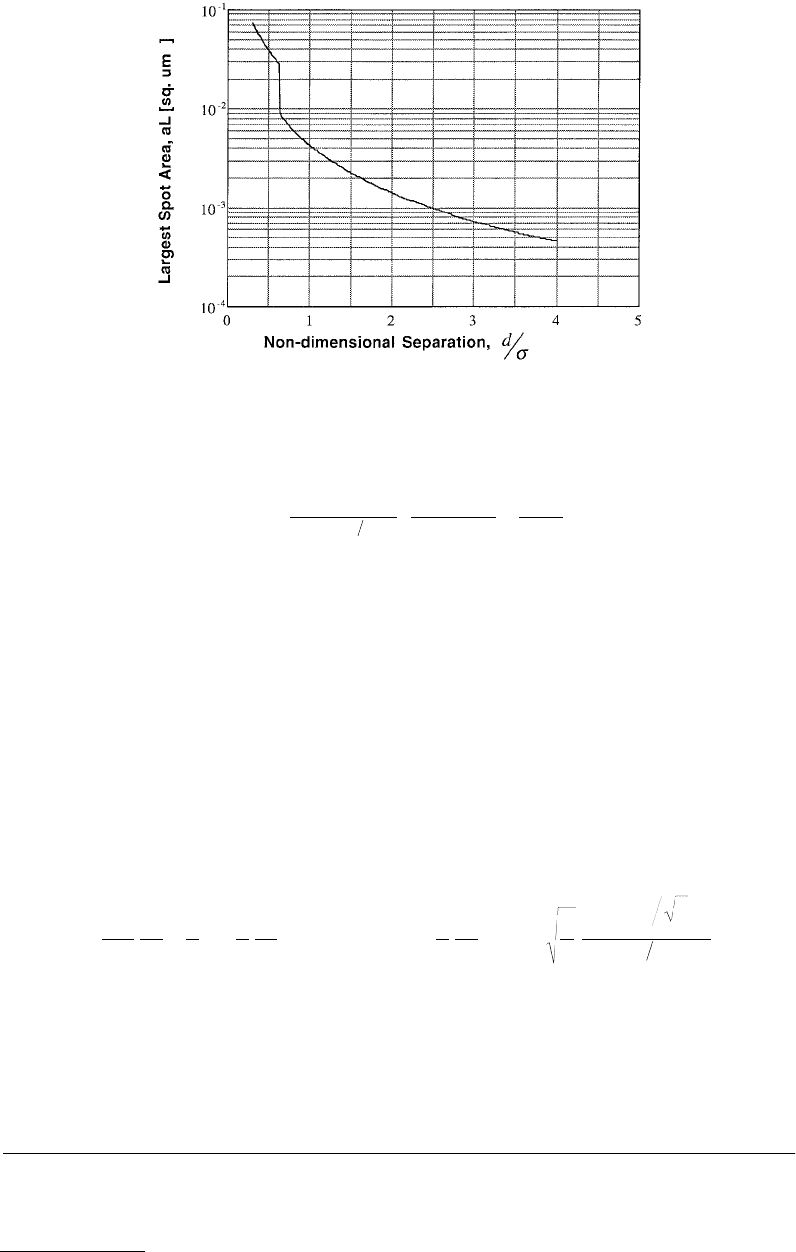
The relation between the largest contact spot, a
L
, and the nondimensional separation d/σ for a magnetic
tape surface in Figure 4.28. It is assumed here that φ = 0.072 and a
c
= 0.35 µm
2
as will be shown in the
next section. The relation between curvature k(a) as a function of a is obtained from the generalized
roughness characterization technique discussed in Section 4.3.4.
4.5 Contact Mechanics of Rough Surfaces
In Section 4.4, the size distributions of contact spots were obtained as a function of the separation d
between two surface mean planes as well as the height distribution, g(z), and standard deviation, σ, of
FIGURE 4.28 Relation between the largest contact spot, a
L
, and the nondimensional separation d/σ between the
magnetic tape A surface and a flat hard plane.
na
AG gd
a
Da
G
D
p
a
D
D
D
D
()
=
()
π
π
+
−
−
()
+
()
−
()
−
()
1
12
1
21
4
2
4
φ
naada naada A d
p
a
e
a
a
a
c
c
L
()
+
()
=
()
∫∫
0
Ω
ka
k
dk
da
a
k
dk
da
da k a
a
k
dk
da
da
d
e
aa
d
cc
()
−
π
++
+
()
+
=π
π
∫∫
−
φ
σσ
σ
2
1
2
11
2
2
3
00
2
22
erfc

© 1999 by CRC Press LLC
the equivalent surface. However, a relation between the load F and the separation d occurs is still not yet
obtained. To do so, it is necessary to understand the elastic and the plastic deformations of the surface
asperities in contact. Then one can finally determine the size distributions of contact spots for a given
load and material properties. That will become the starting point to study friction, wear, and other
tribological phenomena.
Static contact between two surfaces can be modeled as the contact between an equivalent surface and
a flat hard plane as discussed in Appendix 4.3. In the past, several theories of elastic–plastic contact
between a rough surface and a flat hard plane have been proposed. The most popular of these is the
Greenwood–Williamson (GW) (1966) model. A brief description of this model is presented here and
more descriptions are available in several review papers and textbooks. This subsection will present a
critical review of when the GW model can and cannot be applied. Note that the GW model is taken as
representative of the several “constant-curvature” models available in the literature
(McCool, 1986).
4.5.1 Greenwood–Williamson Model
4.5.1.1 The Model
The GW model assumes the surface to be composed of hemispherical asperities all having the same
radius of curvature R. The summit heights or asperity peaks are distributed randomly about a mean
summit plane and follow a Gaussian distribution with a standard deviation, σ
s
, as shown in Figure 4.29.
Note that the distribution of the summits is not the same as that of the surface. The summits are presumed
to be uniformly distributed over the rough surface with a known density D
sum
of summits per unit area.
The probability, Ω
0
, that a randomly selected summit has a height in excess of some value d, can be
found from the cumulative probability distribution as
(4.5.1)
where
–
z
s
is the summit height normalized by the summit rms height, σ
s
. This is the probability that a
randomly selected summit will contact a smooth hard plane when the distance between the plane and
the surface mean is equal to d. Since the surface density of summits is D
sum
, the average expected number
of contacts, n, per unit area is
(4.5.2)
For a summit of height, z
s
, which exceeds the separation, d, the deformation, w, is equal to w = z
s
– d.
Then according to Hertz’s theory of elastic contact (Timoshenko and Goodier, 1970; Johnson, 1985)
between a sphere and flat plane, the area of contact for this summit is
FIGURE 4.29 Model of surface roughness used in the GW (1966) model of contact mechanics.
Ω
0
d
gz dz
s
ss
d
s
σ
σ
=
()
∞
∫
nD
d
s
=
sum
Ω
0
σ
© 1999 by CRC Press LLC
(4.5.3)
The corresponding asperity load is
(4.5.4)
where E is the elastic modulus of the equivalent surface and is given as
(4.5.5)
where ν is the Poisson’s ratio and the subscripts 1 and 2 correspond to the two surfaces.
Using these expressions for microcontact of a single asperity, the expected values of the total area of
contact, A
r
, and load, F
n
, can be found as
(4.5.6)
where Ω
n
(t) is equal to
(4.5.7)
The GW model contains three parameters that need input from the roughness characteristics — R,
σ
s
, and D
sum
. Nayak (1971, 1973) used statistical analysis to show that their values depend on the variances
of the surface height, σ
2
, the surface slope, σ′
2
, and the surface curvature, σ″
2
. The final expression for
the real area of contact and load reduces to
(4.5.8)
where α is a nondimensional parameter defined as
(4.5.9)
It is interesting to note that a plot of A
r
vs. F
n
is essentially a plot of Ω
1
vs. Ω
3/2
. If a Gaussian distribution
is used for the surface height distribution, it can be shown that this follows a power law A
r
≈ F
n
0.95
.More
details of the GW model, in particular for plastic deformation, and other theories of contact can be found
in McCool
(1986).
aRwRzd
s
=π =π −
()
fERw ERzd
s
==−
()
4
3
12 32
4
3
12
32
1
11
1
2
1
2
2
2
E
v
E
v
E
=
−
+
−
A
A
RD
d
F
A
ER D
d
r
a
s
s
n
a
s
s
=π
=
σ
σ
σ
σ
sum
sum
Ω
Ω
1
12 32
32
4
3
Ω
n
n
t
txtgxdx
()
=−
()()
∞
∫
A
A
d
F
A
E
d
r
as
n
as
=−
()
=
′
−
()
0 064 0 897
0 033 0 897
12
1
34
32
..
..
α
σ
σα
σ
Ω
Ω
α
σσ
σ
=
′′
′
2
2
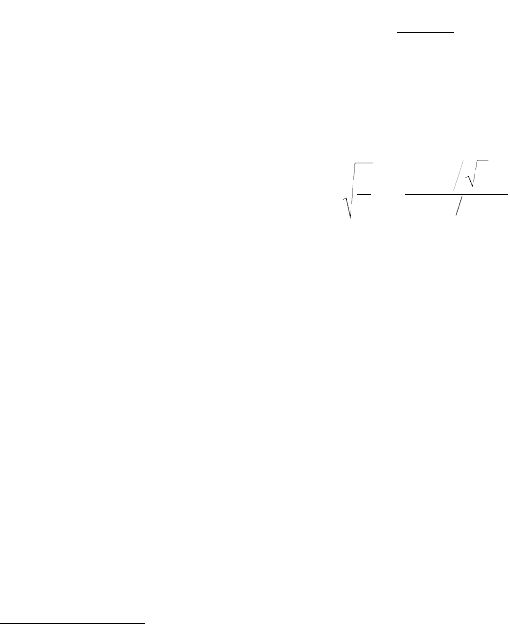
© 1999 by CRC Press LLC
4.5.1.2 A Critique
The GW model is based on the assumption that all the asperities have the same radius of curvature R.
Therefore, the requirement of the GW model is that the surface must be made up of asperities of a single
length scale. The question is whether or not real surfaces follow this behavior. Polycrystalline materials,
which have a very narrow distribution of grain sizes, fit this requirement since they can have surfaces
whose asperities are made up of a single grain. Also, machining processes such as turning, shaping, or
milling can produce a textured surface that contain grooves made by moving the tool at a certain feed
rate. Although the surface will be highly anisotropic, with texture marks only in one direction, the profile
in one direction will be sinusoidal-like and can fit the description of the GW model. In both these cases,
there exists a dominant surface length scale — the grain size for a polycrystalline surface or the texture
grooves for a machined surface. The assumption of a constant-radius asperities of the GW model suggests
that the model is applicable when a surface contains such a dominant length scale.
However, when a surface contains multiple length scales with no dominant scale, the GW model cannot
be applicable. This is because the rms slope and curvature depend on the instrument resolution for
surfaces with multiple length scales. In addition, the rms height can sometimes be instrument dependent
as we saw earlier. Note that multiscale surfaces can, but need not be, fractal in structure. In these cases,
the assumption of constant-radius asperities of the GW model is not valid. In addition, the parameter
α in Equation 4.5.9 is also scale dependent, making the predictions of the GW model questionable for
multiscale surfaces.
In Section 4.2, it was emphasized that an important parameter necessary for tribological analysis is
the size distribution, n(a). However, the GW model does not directly provide this information but gives
the total real area of contact A
r
. This can only be useful in studying friction and wear if τ(a) and
·
v(a) in
Equations 4.2.1 and 4.2.2 are independent of the contact spot area a. In general, τ(a) and
·
v(a) do depend
on the area, and therefore the size distribution is necessary. We can derive the distribution using
Equation 4.4.10 to be
(4.5.10)
where R is the radius of asperity curvature and is assumed constant. By using this, the area of the largest
island can be found as
(4.5.11)
if the height distribution is assumed to be Gaussian. Note that for multiscale surfaces, the radius of
curvature R is not a constant, thereby making Equations 4.5.10 and 4.5.11 scale dependent.
To overcome the difficulties of the constant-radius assumption of the GW model, Majumdar and
Bhushan
(1991) proposed a model of elastic and plastic contact between rough fractal surfaces. The
Majumdar–Bhushan (MB) model allows for asperity curvature to vary with size. The results obtained
by this model are quite interesting and at times drastically different from the GW model. The following
analysis gives the development of this model.
4.5.2 Majumdar–Bhushan Model
Consider an asperity of radius of curvature R being deformed by a hard plane as shown in Figure 4.26b.
Initially, the asperity will deform elastically but beyond a critical deformation, δ
c
, the material will deform
inelastically. For ductile materials this would lead to plastic deformations, whereas for brittle materials
fracture would occur. The critical deformation can be written as
(Greenwood and Williamson, 1966)
na
Agd
Ra
a
()
=
()
π
aR
d
e
L
d
=π
π
()
−
2
2
22
2
σ
σ
σ
erfc
