Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

4.5.4 Cantor Set Contact Models

A new approach to modeling contact mechanics between two rough surfaces has recently been explored

(Warren et al., 1996; Warren and Krajcinovic, 1996a). This approach models the surface as a self-afﬁne

Cantor set (see Figure 4.41), such that laterally and vertically the surface is divided further and further

by the recursive algorithm

(4.5.27)

FIGURE 4.39 (a) Histograms of the number of contact spots, n(a)∆a found of a particular range of spot areas for

two different real contact areas. The numbers n(a)∆a area for 1 mm

of apparent area of rigid disk C. (b) Histogram

of the total contact area of spots in a certain size range as a percentage of the apparent area, an(a)∆a/A

. Note that

the percentages of the real area of contact found by adding up the contributions of each bin are not equal to those

claimed. (From Bhushan, B. and Dugger, M. T. (1990), Wear 137, 41–50. With permission.)

Lateral:

Vertical:

The fractal dimension of the surface obtained through this algorithm was derived to be

(4.5.28)

where s is the number of remaining asperities after the recursive algorithm breaks up a big asperity into

s-smaller ones. For example, the surface in Figure 4.41 uses s = 2. The second term in Equation 4.5.28 is

the dimension of the Cantor set, D

= ln(s)/ln(sf

), which breaks up a line into a set of points.

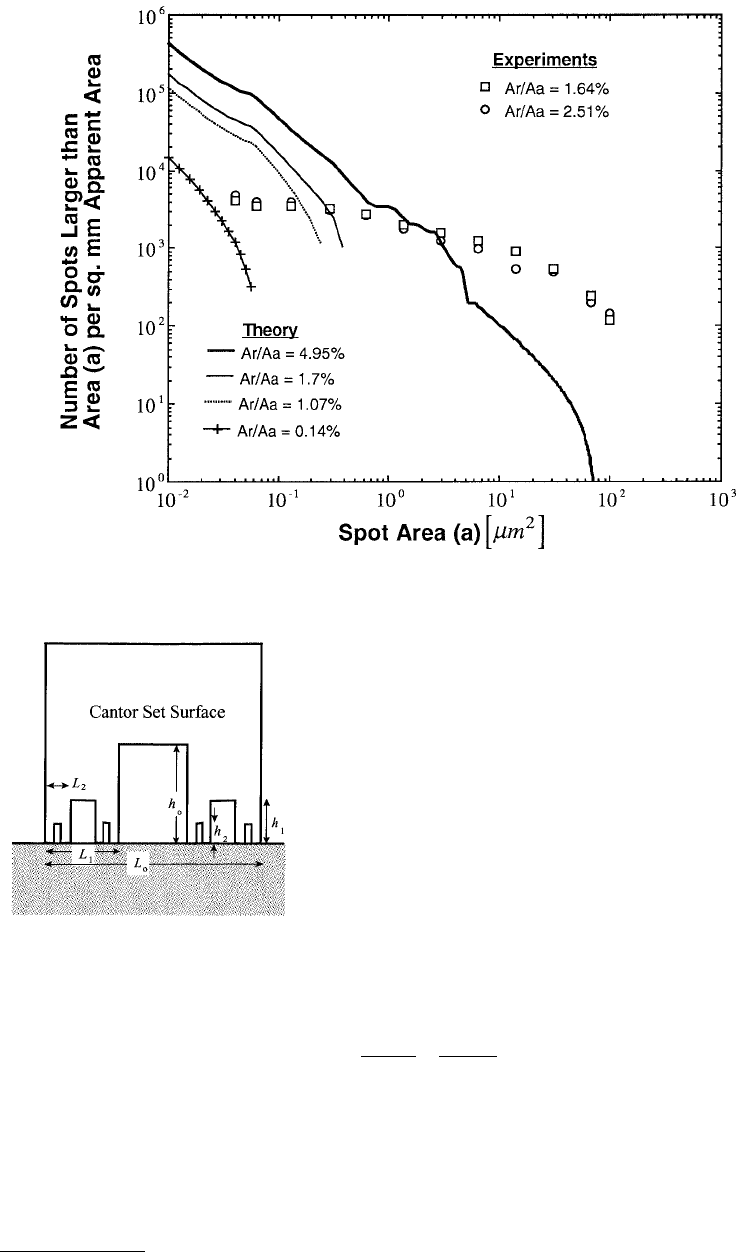
FIGURE 4.40 Comparison of the cumulative size distributions experimentally obtained and theoretically predicted.

FIGURE 4.41 Illustration of a Cantor set surface constructed by

dividing the bottom surface length, L

, into three segments and

removing the middle segment of length L

/3 height, h

. The two other

segments are again broken into three more segments and the middle

segment removed. This recursive algorithm can be continued to

obtain a fractal surface. (From Warren, T. L. et al. (1996), J. Appl.

Mech. 63, 47–53. With permission.)

()

−

()

Warren et al. (1996) ﬁrst developed a model of contact between rigid–perfectly plastic Cantor surface

with a hard ﬂat surface. They found that the load and the real area of contact depended on the defor-

mation, δ, as follows

(4.5.29)

where

(4.5.30)

In a following paper, Warren and Krajcinovic (1996a) considered the contact between randomized Cantor

surfaces which behaved as elastic–perfectly plastic. They found similar correlations as above. A compar-

ison of their predictions with experimental data of Handzel-Powierza et al. (1992) is shown in Figure 4.42.

The advantage of the generalized Cantor surface models over previous fractal models is that the size

and spatial distributions of contact spots is a natural outcome of the recursive algorithm for producing

the surface. This can be very useful for studying the interaction of contact spots during sliding for

phenomena (Warren and Krajcinovic, 1996b) such as stick-slip as well as static and kinetic friction.

However, the models still need to be developed further so as to study realistic surfaces.

4.6 Summary and Future Directions

In this chapter, it was established that surface roughness plays a vital role in microtribology. Rough

surfaces are ubiquitous in nature, and in fact it is rare that a surface is perfectly ﬂat. Therefore, any

realistic study of tribology must include the effects of surface roughness. Contact between two rough

surfaces occurs in the form of discrete spots. It is at these contact spots that all the forces responsible for

friction and wear are generated. These spots are not of the same size and are not uniformly distributed

over the contact interface. Due to the occurrence of surface roughness over several decades of length

scales, ranging from nanometer to millimeter scales, the contact spots have a wide distribution of sizes.

Since interfacial forces have been found to be size dependent, it is very important to determine the size

distribution of contact spots. In addition, dynamic and force interactions between neighboring spots are

also important thus requiring knowledge of the spatial distribution of contact spots.

In order to study the inﬂuence of surface roughness on microtribology, it is ﬁrst necessary to charac-

terize surface roughness in a way that can be easily used to develop models and theories of friction and

wear. What is of vital importance is the size and spatial distribution of contact spots. Such distributions

FIGURE 4.42 Comparison between the predictions of the

Cantor set model (Warren and Krajcinovic, 1996b) and the

experiments (Handzel-Powierza et al., 1992).

∝∝δδ

αα

;

α=

−

+−

are inﬂuenced both by roughness and the contact mechanics of surfaces. In this chapter it was shown

that conventional methods of roughness characterization using rms values of surface height, slope, and

curvature can depend on the resolution of the roughness-measuring instrument and are not unique to

a surface. Therefore, theories based on such parameters can produce misleading results. Roughness

measurements show that most surfaces are composed of small asperities that sit on larger asperities,

which sit on even larger asperities in a hierarchical manner. To characterize this intrinsic multiscale

structure of surface roughness, one must develop techniques that are independent of any length scale.

The hierarchical structure allows fractal geometry to be used to characterize a surface by two scale-

independent parameters — fractal dimension D and amplitude scaling constant G. The latter has units

of length. The relation between the fractal parameters (D and G) and the conventional rms quantities

were also developed. Roughness measurements also showed that there exist some surfaces that do not

follow the scaling hierarchical behavior that fractal characterization demands. A generalized technique

was therefore developed which can characterize both fractal and nonfractal surfaces. This technique can

be used directly in theories of contact mechanics that ﬁnally yield the size distribution of contact spots

needed to develop theories of friction and wear.

A new relation for the size distribution of contact spots was developed in terms of surface height

probability distribution and asperity curvature for different asperity sizes. This relation is general and

can be applied to both fractal and nonfractal surfaces. It was encouraging to ﬁnd that application of the

fractal scaling law for asperity curvature in this general size distribution produced a well-known empirical

power law behavior.

Since the size distribution of contact spots depends not only on the roughness but on the contact

mechanics, the last section dealt with some contact mechanics theories. As representative of classical

theories, the Greenwood–Williamson model was discussed and critiqued. It was shown that the GW

model is applicable only when the surface contains a single dominant roughness scale. Machined surfaces

with periodic grooves or polycrystalline surfaces with a narrow grain size distribution are typical exam-

ples. However, roughness measurements show that many surfaces do not follow this behavior and are

best described by fractal scaling laws. A fractal contact theory showed that for elastic contact between

surfaces, the real area of contact A

and the compressive load F

follow a power law of the form F

≈ A

where the exponent α varies between 0.75 and 1 depending on the fractal dimension D. Since several

surfaces were found to be fractal in certain length regimes and nonfractal in others, there was a need to

develop a generalized theory of contact mechanics. This was developed and was based on the generalized

roughness characterization technique. To demonstrate the use of this theory, contact of a magnetic thin-

ﬁlm rigid disk was studied. The prediction for real area of contact as a function of compressive load was

in close agreement with experimental results. The theory gave the load, real area of contact, and the size

of the largest contact spot as a function of the surface separation. In addition, the size distribution of

contact spots was also determined as a function of the real area of contact, but was found to be in poor

agreement with experimental observations. The reasons for this disagreement were explored.

Despite recent progress in surface roughness characterization and contact mechanics, there still exist

several unanswered questions and unaddressed issues. We have assumed that contact spots of isotropic

surfaces are circular and those of anisotropic surfaces are elliptical. This is not necessarily true since even

for isotropic surfaces, the spots can be elongated in one direction. However, the direction of elongation

is random for isotropic surfaces and nonrandom in anisotropic surfaces. The noncircular contact spots

for isotropic surfaces is clearly shown in the simulation of Figure 4.3. Therefore, the assumption of circular

contact spots is not correct and must be changed. In this chapter we have considered asperity deformation

due to a ﬂat hard plane. The problem of asperity indentation into a ﬂat but softer surface has not been

addressed.

Although this chapter establishes the importance of size and spatial distributions of contact spots in

the development of tribological theories, the issue of spatial distribution has not been addressed at all.

The spatial distribution is needed to study stress interactions and for dynamic interaction between contact

spots. This is very important for high surface deformation cases and for the transition between static

and kinetic friction. The problem lies not in developing a relation for the spatial distribution but

developing a method that can be used in a theory or model of neighboring asperity interaction. That

itself has not been developed or properly understood. Therefore, the question of neighboring asperity

interaction and the spatial distribution is an open problem that needs future attention.

References

Avnir, D. (1989), The Fractal Approach to Heterogeneous Chemistry, J. Wiley, New York.

Bak, P., Tang, C., and Wiesenfeld, K. (1988), “Self-Organized Criticality,” Phys. Rev. A, 38, 364–374.

Barnsley, M. (1988), Fractals Everywhere, Academic Press, San Diego.

Beckmann, P. and Spizzichino, A. (1963), The Scattering of Electromagnetic Waves from Rough Surfaces,

Macmillan, New York.

Berry, M. V. and Hannay, J. H. (1978), “Topography of Random Surfaces,” Nature, 271, 573

Berry, M. V. (1978), “Diffractals,” J. Phys. A, 12, 781–797.

Berry, M. V. and Blackwell, T. M. (1981), “Diffractal Echoes,” J. Phys. A Math. Gen., 14, 3101–3110.

Bhushan, B. (1984a), “Prediction of Surface Parameters in Magnetic Media,” Wear, 95, 19–27.

Bhushan, B. (1984b), “Analysis of the Real Area of Contact between a Polymeric Magnetic Medium and

a Rigid Surface,” J. Tribol., 106, 26–34.

Bhushan, B. (1990), Tribology and Mechanics of Magnetic Storage Devices, Springer-Verlag, New York.

Bhushan, B. and Blackman, G. (1991), “Atomic Force Microscopy of Magnetic Rigid Disks and Sliders

and Its Applications to Tribology,” Trans. ASME, J. Tribol., 113, 452–457.

Bhushan, B. and Doerner, M. F. (1989), “Role of Mechanical Properties and Surface Texture in the Real

Area of Contact of Magnetic Rigid Disks,” J. Tribol., 111, 452–458.

Bhushan, B. and Dugger, M. T. (1990), “Real Contact Area Measurements on Magnetic Rigid Disks,”

Wear, 137, 41–50.

Bhushan, B., Wyant, J. C., and Meiling, J. (1988), “A New Three-Dimensional Non-Contact Digital Optical

Proﬁler,” Wear, 122, 301–312.

Blackman, R. B. and Tuckey, J. W. (1958), The Measurement of Power Spectra, Dover, New York.

Brown, S. R. and Scholz, C. H. (1985), “Closure of Random Elastic Surfaces in Contact,” J. Geophys. Res.,

90(B7), 5531–5545.

Carlson, J. M., Langer, J. S., Shaw, B. E., and Tang, C. (1991), “Intrinsic Properties of a Burridge–Knopoff

Model of an Earthquake Fault,” Phys. Rev. A, 44, 884–897.

Chang, W. R., Etsion, I., and Bogy, D. B. (1987), “An Elastic-Plastic Model for the Contact of Rough

Surfaces,” J. Tribol., 109, 257–263.

Church, E. L. (1988), “Fractal Surface Finish,” Appl. Opt., 27, 1518–1526.

Feder, J. (1988), Fractals, Plenum Press, New York.

Gagnepain, J. J. (1986), “Fractal Approach to Two-Dimensional and Three-Dimensional Surface Rough-

ness,” Wear, 109, 119–126.

Ganti, S. and Bhushan, B. (1995), “Generalized Fractal Analysis and Its Applications to Engineering

Surfaces,” Wear, 180, 17–34.

Greenwood, J. A. and Williamson, J. B. P. (1966), “Contact of Nominally Flat Surfaces,” Proc. R. Soc.

London, A 295, 300–319.

Handzel-Powierza, Z., Klimczak, T., and Polijaniuk, A. (1992), “On the Experimental Veriﬁcation of the

Greenwood-Williamson Model for the Contact of Rough Surfaces,” Wear, 154, 115–124.

Israelachvili, J. N. (1992), Intermolecular and Surface Forces, 2nd ed., Academic Press, San Diego.

Israelachvili, J. N., McGuiggan, P. M., and Homola, A. M. (1988), “Dynamic Properties of Molecularly

Thin Liquid Films,” Science, 240, 189–191.

Johnson, K. L. (1985), Contact Mechanics, Cambridge University Press, Cambridge.

Jordan, D. L., Hollins, R. C., and Jakeman, E. (1986), “Measurement and Characterization of Multiscale

Surfaces,” Wear, 109, 127–134.

Kardar, M., Parisi, G., and Zhang, Y. C. (1986), “Dynamic Scaling of Growing Interfaces,” Phys. Rev. Lett.,

56, 889–892.

Knopoff, L. (1990), “The Modeling of Earthquake Occurrence,” in Disorder and Fracture, (J. C. Charmet,

S. Rou, and E. Guyon, eds.), pp. 284–300 Plenum Press, New York.

Kolmogoroff, A. N. (1941), “Dissipation of Energy in the Locally Isotropic Turbulence,” CR (Doklady)

Acad. Sci. URSS, 32, 16–18. Also in Turbulence — Classic Papers in Statistical Theory (S. K. Fried-

lander and L. Topper, eds.), pp. 159–161, Interscience Publishers, New York, 1961.

Landman, U., Luedtke, W. D., Burnham, N. A., and Colton, R. J. (1990), “Atomistic Mechanisms and

Dynamics of Adhesion, Nanoindentation and Fracture,” Science, 248, 454–461.

Majumdar, A. and Bhushan, B. (1990), “Role of Fractal Geometry in Roughness Characterization and

Contact Mechanics of Surfaces,” ASME J. Tribol., 112, 205–216.

Majumdar, A. and Bhushan, B. (1991), “Fractal Model of Elastic-Plastic Contact between Rough Surfaces,”

ASME J. Tribol., 113, 1–11.

Majumdar, A. and Tien, C. L. (1990), “Fractal Characterization and Simulation of Rough Surfaces,” Wear,

136, 313–327.

Majumdar, A., Bhushan, B., and Tien, C. L. (1991), “Role of Fractal Geometry in Tribology,” Adv. Inf.

Storage Syst., 1., 231–266.

Mandelbrot, B. B. (1967), “How Long is the Coast of Britain? Statistical Self-Similarity and Fractional

Dimension,” Science, 155, 636–638.

Mandelbrot, B. B. (1975), “Stochastic Models for the Earth’s Relief, the Shape and the Fractal Dimension

of the Coastlines, and the Number-Area Rule for Islands,” Proc. Natl. Acad. Sci. U.S.A., 72,

3825–3828.

Mandelbrot, B. B. (1982), The Fractal Geometry of Nature, W. H. Freeman, New York.

Mandelbrot, B. B. (1985), “Self-Afﬁne Fractals and Fractal Dimension,” Phys. Scr., 32, 257–260.

Mate, C. M., McClelland, G. M., Erlandsson, R., and Chiang, S. (1987), “Atomic-Scale Friction of a

Tungsten Tip on a Graphite Surface,” Phys. Rev. Lett., 59, 1942–1945.

McCool, J. I. (1986), “Comparison of Models for the Contact of Rough Surfaces,” Wear, 107, 37–60.

McCool, J. I. (1987), “Relating Proﬁle Instrument Measurements to the Functional Performance of Rough

Surfaces,” J. Tribol., 109, 264–270.

McGuiggan, P., M., Israelachvili, J. N., Gee, M. L., and Homola, A. M. (1989), “Measurements of Static

and Dynamic Interactions of Molecularly Thin Liquid Films between Solid Surfaces,” in New

Materials Approaches to Tribology: Theory and Applications, L. E. Pope, L. L. Fehrenbacher, and

W. O. Winer, eds), Materials Research Society Symposium, 140, 79–88.

Meakin, P. (1987), “Fractal Scaling in Thin Film Condensation and Material Surfaces,” CRC Crit. Rev.

Solid State Mater. Sci., 13, 143–189.

Nayak, P. R. (1971), “Random Process Model of Rough Surfaces,” ASME J. Lubr. Technol., 93, 398–407.

Nayak, P. R. (1973), “Random Process Model of Rough Surfaces in Plastic Contact,” Wear, 26, 305–333.

Oden, P. I., Majumdar, A., Bhushan, B., Padmanabhan, A., and Graham, J. J. (1992), “AFM Imaging,

Roughness Analysis and Contact Mechanics of Magnetic Tape and Head Surfaces,” ASME J. Tribol.,

114, 666–674.

Papoulis, A. (1965), Probability, Random Variables and Stochastic Processes, McGraw Hill, New York.

Peitgen, H. O. and Saupe, D. (1988), The Science of Fractal Images, Springer-Verlag, New York.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P. (1992), Numerical Recipes, 2nd ed.,

Cambridge University Press, New York.

Sayles, R. S. and Thomas, T. R. (1978), “Surface Topography as a Nonstationary Random Process,” Nature,

271, 431–434.

Sornette, A. and Sornette, D. (1989), “Self-Organized Criticality and Earthquakes,” Europhys. Lett., 9,

197–202.

Suh, N. P. (1986), Tribophysics, pp. 35–41, Prentice-Hall, NJ.

Thomas, T. R. (1982), Rough Surfaces, Longman, New York.

Timoshenko, S. and Goodier, J. N. (1970), Theory of Elasticity, 3rd ed., McGraw-Hill, New York.

Vicsek, T, (1989), Fractal Growth Phenomena, World Scientiﬁc, New Jersey.

Voss, R. F. (1988), “Fractals in Nature: From Characterization to Simulation,” in The Science of Fractal

Images, (H. O. Peitgen and D. Saupe, eds.), pp. 21–70, Springer-Verlag, New York.

Warren, T. L. and Krajcinovic, D. (1996a), “Random Cantor Set Models for the Elastic Perfectly Plastic

Contact of Rough Surfaces,” Wear, 196, 1–15.

Warren, T. L. and Krajcinovic, D. (1996b), “A Fractal Model of Static Coefﬁcient of Friction at the Fiber-

Matrix Interface,” Composites: Part B, 27, 421–430.

Warren, T. L., Majumdar, A., and Krajcinovic, D. (1996), “A Fractal Model for the Rigid-Perfectly Plastic

Contact of Rough Surfaces,” J. Appl. Mech., 63, 47–54.

Williams, E. D. and Bartlet, N. C. (1991), “Thermodynamics of Surface Morphology,” Science, 251,

393–400.

Yamada, K., Takeda, N., Kagami, J., and Naoi, T. (1978), “Mechanisms of Elastic Contact and Friction

between Rough Surfaces,” Wear, 48, 15–34.

Appendix 4.1 — RMS Values for Multifractal Surfaces

Roughness measurements have shown that structure function does not always follow a single power law

over a wide range of length scales, but may follow two or more power laws at different length regimes.

This can be mathematically written as

(A4.1.1)

where l

is a transition length scale where the fractal behavior changes. The question is how the rms

height is related to the fractal parameters — D

, D

, G

, and G

. If the length, L, of the measured roughness

sample is smaller than l

, that is, L < l

, then regime 2 is never accessed and the problem can be analyzed

as a single fractal behavior, as shown with the help of Equation 4.3.25. If L > l

, then rms height can

be found as

(A4.1.2)

When the length, L, is much larger than the critical length, l

, that is, L  l

, then the ﬁrst term in

Equation A4.1.2 is dominant. In such a case, the rms height, σ, is dominated by large-scale roughness

of regime 2 and one can again use the relation of Equation 4.3.25 for a single fractal behavior. Note that

in such a case, σ is only related to G

and D

of regime 2 and not to D

and G

, of regime 1.

If the surface proﬁle follows two fractal regimes as shown in Equation A4.1.1 then the rms slope is

equal to

(A4.1.3)

where it is assumed that L > l

> l such that the sample length, L, and the instrument resolution, l, fall

on the different fractal regimes demarcated by the critical length scale, l

. If they fall in the same regime,

then the rms slope is obtained by Equation 4.3.27. Often it is found that L  l

 l, in which case the

rms slope varies as

(A4.1.4)

Here it is found that the rms slope depends on the fractal parameters G

and D

of only fractal regime 1.

This is in contrast with the rms height which depends on the parameters of fractal regime 2.

()

−

()

−

()

for regime 1

for regime 2

112

212

21 2

22 22 22

=+=

−

()

−

()

−

()

−

()

−

()

∞

−

()

−

()

−

()

∫∫

DDD

′

−

()













−

























−

()













−

()

−

()

−

()

−

()

∫∫

−

()

−

()

−

























′

−

()













−

()

Appendix 4.2 — Autocorrelation Function and Fractal Parameters

The structure function, S(τ), can be broken up and written as

(A4.2.1)

where z

is the surface mean height and R(τ,L) is the autocovariance function deﬁned as

(A4.2.2)

It is evident that R(0,L) = σ

(L). Therefore, the autocovariance function is often written as R(τ,L) =

(L)f(τ,L), where f(τ,L) is called the autocorrelation function and is equal to unity for τ = 0. The

autocorrelation function is related to the structure function and the rms height as

(A4.2.3)

When the rms height, σ, is independent of the sample size, L, then it can be characterized by the

structure function model proposed by Berry and Blackwell (1981) given in Equation 4.3.24. By using

Equation 4.3.24 in Equation A4.2.3, the autocorrelation function can be obtained to be

(A4.2.4)

where the correlation length is τ

= G(2σ/G)

1/(2–D)

It is interesting to note that an approximate autocorrelation function that is often used to model rough

surface proﬁles, for optical scattering by rough surfaces in particular

(Beckmann and Spizzichino, 1963;

Church, 1988) is the exponential decay function of the form:

(A4.2.5)

where τ

is called the correlation length. Comparison with Equation A4.2.4 shows that this approximate

function corresponds to a speciﬁc case of D = 1.5 — a Brownian fractal. This can also be veriﬁed another

way. The autocovariance function, σ

f(τ), and the power spectrum are Fourier transforms of each other

such the power spectrum can be written as

zx z zx z dx

zx z zx z zx z zx z dx

LRL

mm mm

ττ

στ

()

−

()

−

()

−

()













()

−

()

−

()

−+

()

−

()

−

()













()

−

()

[]

∫

zx z zx z dx

zx z zx z

imim

ττ

()

−

()

−

()

−

()

−

()

−

()

∫

∑

−

()

∆

()

=−

()

=−













=−

























−

()

−

()

−

()

exp exp

2122

()

=−













exp

(A4.2.6)

By using this, the power spectrum corresponding to the autocorrelation function of Equation A4.2.5 is

found to be

(A4.2.7)

Note that for high spatial frequency, ω  ½ πτ

, this spectrum follows the power law behavior of P(ω) ≈

–2

. When compared to the fractal power spectrum, P(ω) ≈ ω

–(5–2D)

, this corresponds to the Brownian

fractal, D = 1.5.

Appendix 4.3

Consider a reference plane such that the height of surface 1 is z

(x) and that of surface 2 is z

(x) as shown

in Figure A4.3.1. The surface means are separated by a distance d. One can construct an equivalent surface

z(x) = z

(x) – z

(x). The mean height of the equivalent surface is located at a vertical position 〈z〉 = 〈z

〉 –

〈z

〉 = –d from a ﬂat hard plane at z = 0. This hard plane is the contact plane since contact is made

between the two surfaces at any position x when z(x) = z

(x) – z

(x) ≥ 0.

Normalized by the surface means, the equivalent surface is related to surfaces 1 and 2 as follows:

(A4.3.1)

The variance of the equivalent surface can be found as

(A4.3.2)

If the surfaces are statistically uncorrelated, then the last integral in Equation 4.5.2 is equal to zero. Then

the variances of the equivalent surface is equal to the sum of the variances of the two surfaces as σ

+ σ

. Similarly, for uncorrelated surfaces, the structure function and the power spectrum of the

equivalent surface can be written as

(A4.3.3)

Pfidωστ ωττ

()

−

()

−∞

∞

∫

exp

στ

τω

()

+π

()

zx d z x z z x z

()

−

()

−

()

−

()

112 2

()

−

()

−

()













−

()

−

()

−

()

∫

∫∫

zx d dx

zx z zx z

zx z zx z dx

SS S

PPP

τττ

ωωω

()