Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

The second term in the equation for P accounts for the attractive forces which act to deform the

tip–sample geometry, causing the nonrigid materials to bulge out toward each other during the tip–sam-

ple approach. The third term has a prefactor of 1 instead of 2, as is the case for DMT, because of the

reduction in attractive force due to the bulged geometry. That is, the bulge prevents the full attractive

force from being attained. In the equation for δ, the second term represents the distance that the surfaces

deform toward each other. However, the Hertzian functional relationship between penetration depth and

contact radius, δ ~ a

, is retained, and there is no adhesion hysteresis.* The imagery associated with

loading and unloading for Hertz, DMT, and BCP is that they are smooth processes, whereas in the

JKRS model, both loading and unloading are abrupt.

A good exercise is to plot P and δ as a function of a. (P is shown as a function of δ in Figure 5.9.)

How do R, ϖ, and K inﬂuence a?

5.4.2.5 JKRS Mechanics

In the JKRS analysis (Johnson, Kendall, Roberts, Sperling — 1964 and 1971) there are no forces between

the surfaces when they are not in contact, upon contact short-ranged attractive forces suddenly operate

within the contact area, and the tip–sample geometry is not constrained to remain Hertzian. This set of

assumptions applies well to highly adhesive systems that have large radii of curvature and low stiffness.

During unloading, a connective neck is formed between the tip and sample, and contact is ruptured at

negative loads. This causes adhesion hysteresis.

(5.15)

What are the values of a when P = 0 and δ = 0? How do they compare to BCP, DMT, and Hertz?

In the example in Section 5.1, we considered the residue of an eraser binding to paper. This very

compliant material sticking to a nominally ﬂat surface is a good example of a typical JKRS system, where

the material deforms locally in the contact region in response to surface forces, thereby increasing the

residue–paper adhesion over what would be expected for Hertz, DMT, or BCP.

5.4.2.6 Maugis Mechanics

A more complex, yet more accurate, description of sphere–ﬂat mechanics was formulated by Maugis in

1992. It is more accurate in that one does not have to assume a particular limit for the materials properties;

Maugis mechanics applies to all systems, from large compliant spheres with strong adhesion, to small

diamond/diamond systems with low adhesion. The parameter λ,

(5.16)

is used to characterize this spectrum of materials possibilities. As can be seen, large λ is for the more

compliant, adhesive combinations, and vice versa, for small λ. In the limit of inﬁnite λ, the Maugis

equation approaches those of JKRS theory, and the pull-off force goes to –1.5πRϖ. For the limit of λ

equals zero, the system responds like the DMT mechanics, and the pull-off force approaches –2πRϖ.

Measuring the pull-off force is therefore not an accurate method to determine ϖ.

*The values for P and δ at which contact is made and broken, i.e., P = –πRϖ and δ = –(π

Rϖ

), correspond

to the case for the Maugis λ = 0.8785, deﬁned in Section 5.4.2.6. This choice results in a large outward bulge so that

no sharp discontinuities exist in the force curve, yet the mathematics remain simple, in that there is no hysteresis.

A good ﬁt to data is obtained at low loads, less so at higher loads.

=−π

=−













206

In the Maugis model, by analogy with the plastic zone ahead of a crack, the adhesion is represented

by a constant additive traction acting over an annular region around the contact area. The ratio of the

width of the annular region to the radius of the contact area is denoted by m. The set of equations relating

λ, m, a, δ, and P is

(5.17)

Additionally, the theory predicts that an instability always occurs when the tip–sample force is con-

trolled (with the exception of λ = 0), and, when the tip–sample displacement is controlled, the instability

occurs for λ larger than about 0.94. The instability, the jump from a ﬁnite contact radius to none, generates

adhesion hysteresis.

5.4.2.7 Comparison of the Five Theories

In each previous subsection one theory was presented. There may be cases when the assumptions made

for a given approach do not exactly describe the materials combinations or the tip–sample geometry.

The Maugis mechanics clearly has an advantage here, as all systems, from rubber/rubber to diamond/dia-

mond are adequately described. Table 5.2 presents the major assumptions and limitations inherent to

each theory, while Table 5.3 summarizes the pertinent normalized equations. You should be able to

progress from Equations 5.18, below, and Equations 5.11 through 5.17 to Table 5.3 by substitution. The

deﬁnitions of the normalized contact radius

–

A, load

–

P, and the penetration depth

–

∆ are

(5.18)

TABLE 5.2 Comparison of the Contact Mechanical Theories Discussed in this Chapter

Theory Assumptions Limitations

Hertz No surface forces Not appropriate for low loads if surface forces present

DMT Long-ranged surface forces act only outside

contact area

May underestimate contact area due to restricted

geometry

Geometry constrained to be Hertzian Applies to low λ systems only

BCP Long-ranged surface forces act only outside

contact area

May underestimate pull-off force due to Hertzian

function for geometry

Hertzian functional dependence for

geometry

Applies to moderate λ systems

JKRS Short-ranged surface forces act only inside

contact area

May underestimate loading due to surface forces

Contact geometry allowed to deform Applies to high λ systems only

Maugis Periphery of tip–sample interface modeled

as a crack that fails at its theoretical strength

Solution analytical, but parametric equations

Applies to all values of λ

12 1

11 1

22 2













−+ −

()

−

[]













−+ − −

[]

=−













−

=−







λϖ

mm m

arctan

arctan ,







−+ −

[]

22 2

11mm marctan .

radius ,A













Figures 5.9 and 5.10, in which the normalized load is plotted as a function of normalized indentation

depth, compare the ﬁve theories that we have summarized. Much is missing from what is presented here:

the effects of plastic deformation, viscoelasticity, surface roughness, and chemical bonding, to name just

a few. On the other hand, the equations in this section can be applied to a wide variety of materials

systems, and the plots of Figures 5.9 and 5.10 show how even completely elastic systems give rise to

adhesion hysteresis and therefore energy dissipation. This may be a useful way of understanding frictional

behavior.

5.4.3 Adhesion in Nanometer-Sized Contacts

In the previous subsection on contact mechanics and adhesion hysteresis, two important assumptions

to the discussions were (1) that even though adhesion hysteresis was possible, there was no permanent

damage to either the tip or sample; and (2) that the materials involved were not composed of discrete

particles, but rather were continuous media. These can be dangerous assumptions for the case of nanom-

eter-sized contacts. In this section, we shall show how the tip–sample system can widely stray from

continuum elastic theory.

TABLE 5.3 Summary Table of the Contact Mechanical Theories

Theory Normalized equations

Hertz

DMT

BCP

JKRS

Maugis

∆

=−

∆

PA A

=− −

=−

1∆

PA A A

=−

∆

12 1

11 1

22 2

322 2 2

=−+− −+−+− −

=− −+ −

=− −

()

[]

λλ

mm m

PA A m m m

arctan arctan ,

arctan

∆

load

depth













∆

5.4.3.1 Surface Forces Alone Can Induce Plasticity

If surface forces are high, and the contact radius small, a great deal of pressure can build up underneath

the tip even in the absence of an externally applied load. In some cases, surface forces alone can induce

plasticity. Plastic deformation, that is, permanent deformation, can generate hysteresis in both the positive

and negative load sections of force–indentation depth curves. Whereas energy loss due to elastic defor-

mation occurs in the last few nanometers before contact is broken, plasticity-related energy dissipation

can happen at both high and low indentation depths.

We deﬁne Π as an effective peripheral attractive force, as in Equation 5.14 above. U

represents the

surface energy, equal to –πa

ϖ, and δ is the indentation depth changed by the load P.

It can be shown that the contact radius a increases in such a way that it is as if a load of P + 2Π were

acting upon it, as opposed to just P + Π.

For a wide range of materials parameters, the following approximation predicts a load for the onset of

plasticity.

where Y is the elastic limit (yield stress). The smaller the curvature radius, the higher the pressure beneath

the tip. From the last three equations, a radius can be calculated at which and below which plasticity can

be expected. It is R ≈ 0.7ϖK

, an expression that depends heavily on the modulus and yield stress. As

an example, consider clean metals in vacuum: their moduli are of the order of 100 GPa, their yield stresses

about 10 GPa, their works of adhesion approximately 3 J/m

. We therefore expect that for tip radii less

than or equal to around 20 nm, the metal will plastically deform. Covering the surface with even one

layer of a low-surface-energy material can reduce the work of adhesion by one or even two orders of

magnitude, so that radii of a few tens of nanometers no longer permanently deform the materials. But

the main point here is that the assumption of perfectly elastic behavior for SPM experiments and many

tribological systems is not necessarily valid.

5.4.3.2 Molecular Dynamics Simulations

In Section 5.4.2, we introduced continuum contact mechanical theories, where the tip and sample were

modeled as continuous media. At the scale of SPM experiments, this view is not always appropriate.

Matter is composed of atoms, and its fundamental structure should be reﬂected in theoretical models of

tip–sample interactions. One way of accounting for the atomistic nature of matter is with molecular

dynamics simulations (Rapaport, 1995).

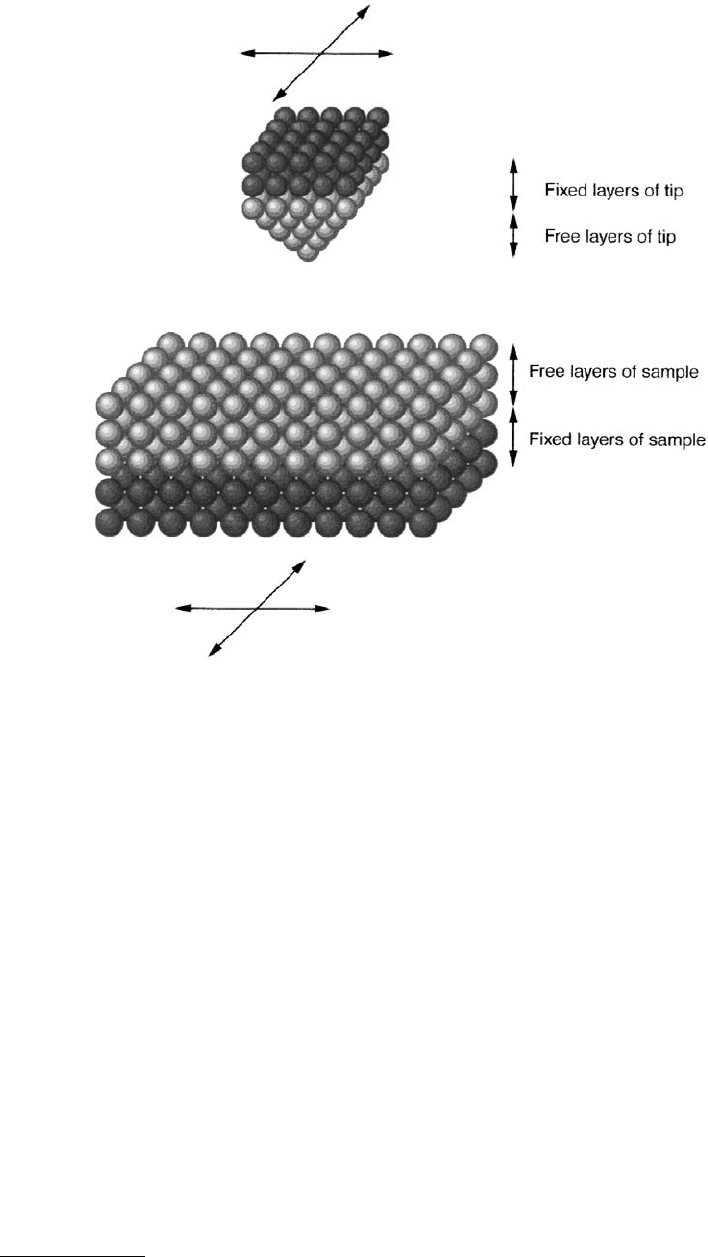
In a molecular dynamics simulation, a set of atoms is modeled. They are arranged into a desired

pattern, e.g., a tip held over a sample, as in Figure 5.11. Typically, a few layers of atoms are held ﬁxed to

a speciﬁed position, but allowed to vibrate about their respective origins so that their ﬂuctuations reﬂect

the system temperature. The remaining atoms are free to respond to whatever forces may act upon them.

They may change their position or energy. The ﬁxed layers of atoms may be moved toward and then

away from each other so as to model indentation experiments; or, if they are slid sideways with respect

to each other, they model friction. The velocity and position of each atom are calculated as a function

of time; these data are stored and later analyzed to yield snapshots, or even movies, of the system evolution.

Simulated force curves can also be obtained.

Π=−

∂













ϖ3

+Π=2

PaY+Π=π15 11

..,

Keeping track of the position and velocity of several thousand atoms requires an enormous amount

of computer time. A major consideration in molecular dynamics simulations is how many atoms can

one afford to study, and what should the simulated time be? “Afford,” in this sense, is how long the

researcher is willing to wait for the results? The more atoms, the more realistic the simulations because

the typical real-world tip of 50 nm radius may comprise a million atoms in its lower hemisphere. Similarly,

the typical physical experiment takes place over orders of magnitude longer times than the usual computer

experiment.

Another important decision in molecular dynamics simulations is the choice of interatomic potentials.

If a simple interatomic potential, such as Lennard–Jones (α/r

– β/r

), is used, the results apply very

well to noble gas solids, where the atoms only marginally interact with each other. The results do not

reﬂect the directionality of covalent chemical bonds, or the sea of electrons surrounding the atomic nuclei

in metals. Lennard–Jones potentials are employed because they are computationally “inexpensive,” in

other words, fast. Computationally expensive potentials are implemented when behavior speciﬁc to

bonding or the plasticity of metals is of interest.

Comparing predictions from continuum mechanics and molecular dynamics is very interesting. Both

approaches yield about the same results for the expected attractive force and neck height for the tip–sam-

ple contact. Some further examples of what is predicted from molecular dynamics are the transfer of

atoms from the lower surface energy material to the higher, the ductile extension of the more plastic

FIGURE 5.11 Typical setup for a molecular dynamics simulation. Atoms are arranged to form a tip and sample,

where several layers of atoms far from the contact point act as thermal sinks and are free only to vibrate around their

ﬁxed central positions. The free atoms move in response to the forces acting upon them. Two-dimensional boundary

conditions are indicated by the crossed arrows.

material upon tip retraction, and the elongation of the resulting connective neck between tip and sample

by atomic units. By simulating nanoscale tip–sample interactions via molecular dynamics, more phys-

ical phenomena can be revealed than by using continuum mechanics theories, but the effort required

for the “computer experiments” is much greater than for traditional modeling.

5.4.3.3 Experimental Observations

The values for the parameters in Equation 5.16 usually give a Maugis λ of the order of 1 for AFM

experiments in air or dry nitrogen. This inconveniently lies between the JKRS and DMT extremes.

Accordingly, it is not easy to predict if there will be signiﬁcant elastic adhesion hysteresis during an

experiment.

Gross plastic behavior can usually be observed in SPM images. If permanent damage occurs, images

evolve as a function of time. Often people zoom out after scanning a small area to compare the original

scan region with neighboring ones. Small changes, such as plastic deformation below the sample surface,

are more difﬁcult to spot by this imaging method. If good force curve acquisition is possible with your

instrument, it is best to check the reversibility of the force curve up to the load at which the images

are collected.

It has been observed in ultrahigh vacuum experiments that just one layer of adsorbate on a clean

surface is enough to change adhesional behavior drastically from plastic to elastic. In general, one can

apply elastic theory to adsorbate-covered surfaces, and reserve the effects of plasticity for very clean,

high-surface-energy systems such as metals in vacuum. One known exception to this is gold, which has

a low yield stress and is very ductile, and forms long extruded “atomic wires” between the tip and samples

upon unloading.

5.4.4 Overview

In this section, we have tried to distinguish among (1) anelastic energy dissipation, where the near-surface

region absorbs energy as does a dashpot; (2) elastic energy dissipation, where the near-surface region of

a complaint sample is temporarily deformed into a connective neck; and (3) plastic energy dissipation,

where the near-surface region is permanently changed. All three processes create adhesion hysteresis

in force curves, with the result that adhesive forces are greater in magnitude than attractive forces. If

the force curve data are acquired quasi-statically, then anelasticity is not a factor. The ﬁrst surface layer

has an important role in determining the work of adhesion for the asperity and ﬂat. The yield stress of

the near surface, relative to the work of adhesion and the local curvature radius, ﬁxes the dissipation

process, i.e., elastic or plastic. The elastic modulus of the near surface, relative to the work of adhesion

and the local curvature radius, determines the amount of energy dissipated for the elastic case.

5.5 Closing Words

5.5.1 Interpreting Your Data

It is essential that your instrument is well calibrated, that you understand the sources of error, and

that you avoid, or at least understand, artifacts. As you interpret your data, pay attention not only to

the magnitude of the surface and adhesive forces, but also to the force–distance relationship (Figures 5.6

through 5.8). This can help you decide which forces or processes are active. Naturally, more than one

process may be operative at the same time. When considering the results of molecular dynamics simu-

lations, remember that computer experiments are a logical result of the assumptions that were made

when the program was written. For example, many simulations neglect the fact that electrons have spin,

so that normally magnetic materials may not have magnetic moments in a simulation. Magnetic forces

can overpower other effects, and this may or may not lead to difﬁculties when comparing computer with

real-world experiments.

The concepts discussed in this chapter will be most helpful to you if you are interpreting your

nanotribological results in terms of adhesion hysteresis. One should keep in mind that there are other

approaches to understanding friction; more than one conceptual framework may be useful for a given

situation. Coulomb, 200 years ago, proposed the “cobblestone” theory of friction, where surface asperities

act as cobblestones in a street; the bigger the asperities, the rougher the ride, and the more energy is used

for travel. Modern experiments show that even on atomically ﬂat surfaces the molecular packing and tilt

of long-chained hydrocarbon monolayers affect the frictional response. Bowden and Tabor (1950, 1964)

understood the friction and wear of metal–metal sliding in terms of the plastic deformation of asperity

contacts.

5.5.2 Outlook

Part of the excitement in nanotribology is due to the great intellectual simpliﬁcation associated with the

routine way in which we can now make single point contacts between the tip of an SPM and a sample

surface. In this chapter, we have tried to introduce to readers those ideas, equations, and concepts that

should help speed them on the way to a good grasp of the surface forces and adhesion interactions

relevant to this growing ﬁeld. Of course, the gap between laboratory experiments that study one single

contact and the real world where thousands or millions of asperities are involved remains enormous,

and it is not clear if the lubrication engineer will ever make practical use of nanotribology. But it is hoped

that at least we have broadened the reader’s appreciation of asperity interactions.

We close with a list of questions that may stimulate future work.

• What are the effects of water vapor and surface adsorbates in friction force measurements?

• How does friction affect the imaging mechanisms in scanning probe microscopy?

• Do existing theories quantitatively account for all of the features of force curves?

• To what extent do traditional continuum mechanics explain nanometer-scale tribological pro-

cesses, and how well do they agree with atomistic simulations?

• Can we develop fundamental understanding of friction, lubrication, and wear?

The interpretation of surface forces and adhesion measurements is challenging. Even if you under-

stand your instrumental artifacts, and are conﬁdent about the interpretation of your data, you must

still put your work in the context of the research and current thinking of other groups. The future

prospects for continued intriguing research in nanotribology are excellent.

Acknowledgments

The timely work of F. Oulevey on some of the graphics is very much appreciated. F. Hutson was kind to

review the manuscript.

References

Bhushan, B. (1997), Micro/Nanotribology and Its Applications, Vol. E330, Kluwer Academic, Dordrecht.

Bowden, F. P., and Tabor D. (1950, 1964), The Friction and Lubrication of Solids, Parts I & II. Clarendon

Press, Oxford.

Briggs, G. A. D. (1995), Advances in Acoustic Microscopy, Plenum, New York.

Burnham N. A. and Colton, R. J. (1993), “Force Microscopy,” in Scanning Tunneling Microscopy and

Spectroscopy: Theory, Techniques and Applications (D. A. Bonnell, ed.), pp. 191–249, VCH Publish-

ers, New York.

Israelachvili, J. N. (1992), Intermolecular and Surface Forces, Academic Press, New York

Johnson, K. L. (1985), Contact Mechanics, Cambridge University Press, New York.

Rapaport, D. C. (1995), The Art of Molecular Dynamics Simulation, Cambridge University Press, New York.

Singer, I. and Pollock, H. M. (1992), Fundamentals of Friction: Macroscopic and Microscopic Processes,

Vol. E220, Kluwer Academic, Dordrecht.

Colchero, J. et al. “Friction on an Atomic Scale”

Handbook of Micro/Nanotribology.

Ed. Bharat Bhushan

Boca Raton: CRC Press LLC, 1999

Friction on

an Atomic Scale

Jaime Colchero, Ernst Meyer,

and Othmar Marti

6.1 Introduction

6.2 Instrumentation

The Force-Sensing System • The Tip

6.3 Experiments

Atomic-Scale Imaging of the Friction Force • Thin Films and

Boundary Lubrication • Nanocontacts • Quartz

Microbalance Experiments in Tribology

6.4 Modeling of an SFFM

Resolution in SFFM • Deformation of Tip and Sample •

Modeling of SFM and SFFM: Energy Dissipation on an

Atomic Scale

6.5 Summary

Acknowledgments

References

6.1 Introduction

The science of friction, i.e., tribology, is possibly together with astronomy one of the oldest sciences.

Human interest in astronomy has many reasons, the awe experienced when observing the dark and

endless sky, the fear associated with phenomena such as eclipses, meteorites, or comets, and perhaps also

practical issues such as the prediction of seasons, tides, or possible ﬂoods. By contrast, the interest in

tribology is purlye practical: to move mechanical pieces past each other as easily as possible. This goal

has not changed essentially since tribology was born. Ultimately, the person who a few thousand years

ago had the brilliant idea to pour water between two mechanical pieces was working on the same problem

as the expert tribologist today, the only difference being their level of knowledge. A better understanding

of friction and wear could save an enormous amount of energy and money, which would be positive for

economy and ecology. On the other hand, friction is not only negative, since it is fundamental for basic

technological applications: brakes as well as screws are based on friction.

The ﬁrst approach to tribology is due to Leonardo da Vinci at the beginning of the 15th century. In a

certain sense he introduced the idea of a friction coefﬁcient. For smooth surfaces he found that “friction

corresponds to one fourth its weight”; in other words, he assumed a friction coefﬁcient of 0.25. To appreciate

these tribological studies one should bear in mind that the modern concept of force was not introduced

until about 200 years later. The next tribologist was Amontons around the year 1700. Surprisingly, the

model he proposed to explain the origin of friction is still quite modern. According to Amontons, surfaces

are tilted on a microscopic scale. Therefore, when two surfaces are pressed against each other and moved,

a certain lateral force is needed to lift the surfaces against the loading force. Assuming that no friction

occurs between the tilted surfaces, one immediately ﬁnds from purely geometric arguments

where

is the tilting angle on a microscopic scale. This model relates the friction to the microscopic

structure of the surface. Today we know that this model is too simple to explain the friction on a

macroscopic scale, i.e., everyday friction. In fact, it is well known that surfaces touch each other at many

microasperities and that the shearing of these microasperities is responsible for friction (Bowden and

Tabor, 1950). Within this model the friction coefﬁcient is related to such parameters as shear strength

and hardness of the surfaces. On an atomic scale, however, the mechanism responsible for friction is

different. As will be discussed in more detail in this chapter, the model for explaining energy dissipation

in a scanning force microscope (SFM) is that the tip has to overcome the potential well between adjacent

atoms of the surface. For certain experimental conditions, which are in practice almost always realized,

the tip jumps from one stable equilibrium position on the surface to another. This process is not reversible,

leads to energy dissipation, and, therefore, on average to a friction force. The similarity between Amon-

tons’ model of friction and these modern models for friction on an atomic scale is evident. In both cases

asperities have to be passed, the only difference is the length scale of these asperities, in the ﬁrst case

assumed to be microscopic, in the second case atomic.

Although tribology is an old science, and in spite of the efforts and progress made by scientists and

engineers, tribology is still far from being a well-understood subject, in fact (Maugis, 1982),

“It is incredible that, all properties being known (surface energy, elastic properties, loss properties), a

friction coefﬁcient cannot be found by an

a priori

calculation.”

This is in contrast to other ﬁelds in physics, such as statistical physics, quantum mechanics, relativity,

or gauge ﬁeld theories, which in spite of being much younger are already well established and serve as

fundamental theories for more complex problems such as solid state physics, astronomy and cosmology,

or particle physics. A fundamental theory of friction does not exist. Moreover, and although recently

considerable progress has been made, the determination of relevant tribological phenomena from ﬁrst

principles is right now a very complicated task, indeed (Anonymous, 1995):

“What is needed … would be to calculate the results of moving a probe of known Miller surface of a

perfect crystal and calculate how energy is generated in the various phonon modes of the crystal as a

function of time.”

From another point of view, the difﬁculties encountered in tribology are not so surprising taking into

account the diversity of phenomena which in principle can contribute to the process of friction. In fact,

for a detailed understanding of friction the precise nature of the surfaces and their mutual interaction

have to be known. Adsorbed ﬁlms which can serve as lubricants, surface roughness, oxide layers, and

maybe even defects and surface reconstructions determine the tribological properties of surfaces. The

essential complexity of friction has been described very accurately by Dowson (1979):

“… If an understanding of the nature of surfaces calls for such sophisticated physical, chemical,

mathematical, materials and engineering studies in both macro and molecular terms, how much more

challenging is the subject of … interacting surfaces in relative motion.”

An additional problem in tribology is that until recently it has not been possible to ﬁnd a simple

experimental system which would serve as a model system. This contrasts with other ﬁelds in physics.

There, complex physical situations can usually be reduced to much simpler and basic ones where theories

can be developed and tested under well-deﬁned experimental conditions. Note that it is not enough if

such a system can be thought of theoretically. For testing the theory this system has to be constructed

lat load

()

⋅tan