Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

then bends again in the new scan direction — the signal polarity therefore changes sign — until the

critical force is reached. Then the whole stock-slip process starts again but with opposite polarity. We

note that the area enclosed by the lateral force curve has the dimension of energy and, in fact, this area

represents the energy dissipated during each scanning cycle. A more precise description of stick-slip

behavior is given in Section 6.4.3.3.

If the sample is scanned slowly in the direction perpendicular to the fast scan which corresponds to

the acquisition of the lateral force curves, then two-dimensional maps of the lateral force are obtained,

as shown in Figure 6.7. These two ﬁgures illustrate the two usual ways of representing data in SFFM.

From the lateral force curve the friction is directly read off: the friction corresponds to half the height

of the lateral force curve. Two-dimensional images, on the other hand, show the variation of the friction

on different spots on the sample. Most conveniently, two-dimensional images with the data corresponding

to the back-and-forth scan are acquired simultaneously; then all data is available and one can choose

between the most convenient representation.

The amazing and puzzling feature about the two ﬁgures shown is the fact that they show a variation

of the lateral force that corresponds to the atomic periodicity. For a tungsten tip with a typical radius of

50 nm on graphite (E

HOPG

 5GPa) and loading forces of up to 100 µN, Equation 6.16 leads to a contact

radius of almost 100 nm, corresponding to a contact of more than 100,000 unit cells. One possible

explanation for this evident misﬁt between contact area and apparent resolution is that imaging is due

to a ﬂake of surface material which adheres to the tip and is dragged over the surface. Since the periodicity

of the “tip”-ﬂake and the sample is equal, this would lead to a coherent interaction and thus to the

observed atomic periodicity. This explanation is very plausible for the present experiment and generally

for experiments involving layered surface materials and high loads. Similar experiments performed by

the same group on mica, which is also a layered material, showed again atomic resolution of the friction

force (Erlandson et al., 1988).

These ﬁrst experiments had two major difﬁculties. First, the normal force could not be controlled

directly but had to be estimated. Second, the cantilevers used had a high force constant. The rapid

development of SFM led, on the one hand, to microfabricated cantilevers with integrated tips (Albrecht,

1989; Albrecht et al., 1990; Akamine et al., 1990; Wolter et al., 1991) and, on the other hand, to new

detection schemes, in particular to the optical beam deﬂection method (Meyer and Amer, 1988, 1990b;

Alexander et al., 1989; Marti et al., 1990). Historically, it is interesting to note that both developments —

and not only the second as is commonly assumed — were equally important for the success of SFFM.

In fact, a year before the successful application of the optical beam deﬂection method for measuring

lateral forces two of the authors had already tried this technique with the ﬁrst microfabricated cantilevers.

However, since these ﬁrst cantilevers lacked the tip which induces the bending moment that causes the

cantilever to twist, no reasonable signal corresponding to lateral forces was detected.

FIGURE 6.7 Two-dimensional map of the lateral force

recorded as the tip is moved 2 nm from left to right. The

spatial variation of the lateral force has the periodicity of

the HPOG surface. (From Mate, C. M. et al. Phys. Rev. Lett.

59, 1942–1945. With permission.)

The optical beam deﬂection method in combination with microfabricated cantilevers and integrated

tips not only allowed the simultaneous measurement of normal and lateral forces, it also increased the

lateral force resolution by more than one order of magnitude. Figure 6.8 shows an image corresponding

to the topographic signal measured simultaneously with the lateral force taken at an estimated loading

force of about 20 nN. As in the previously described experiment, the lateral force signal shows the typical

stick-slip behavior. Surprisingly, the slip motion occurs near a minimum in the topographic signal and

not near its maximum, which is what is predicted by usual models. One possible explanation of this

behavior is that a delay in the topographic signal is introduced due to the ﬁnite response time of the

feedback loop.

A detailed study of the relative phase between the topographic and the lateral force signal is due to

Ruan and Bushan (1994b). In this work topographic and lateral force images of a HPOG surface were

acquired simultaneously. The surface was imaged with commercial microfabricated Si

cantilevers

under ambient conditions. The corresponding raw data as well as the Fourier ﬁltered images are seen in

Figure 6.9. From the ﬁltered images, the relative displacement of the two images is easily determined: the

lattices corresponding to topographic and lateral force signals are shifted by about one third unit cell.

To explain this phenomenon, the authors argue that the lateral force signal is not necessarily always due

to stick-slip motion and to dissipative phenomena. In fact, the lateral force can be decomposed in a

conservative and a nonconservative component. The latter component is due to energy dissipation and

is proportional to the area enclosed by the lateral force curve (see Figure 6.6 or 6.32). Only this noncon-

servative component can be considered a friction force. The conservative component, on the other hand,

is not related to energy dissipation. For example, if lateral forces act on the tip in noncontact SFM in

such a way that no stick-slip is observed and correspondingly no energy is dissipated, then this lateral

force would be truly conservative.

If stick-slip occurs, then the slip distance is smaller than the interatomic distance, but of this order.

From the data shown in Figure 6.9 the lateral displacement of the tip during slip is calculated to be

0.01 nm and thus much less than the 0.1 nm between maxima and minima in the images shown, which

can be considered a typical slipping distance. From this the authors conclude that the lateral force signal

measured is not simply due to the stick-slip motion of the tip. The authors propose that the signal

observed is due to a conservative interatomic interaction which results in an atomic-scale variation of

FIGURE 6.8 Oscilloscope traces corresponding to the topography (upper trace) and to the lateral force (lower trace)

taken as the tip scans over a mica surface. Both traces were acquired simultaneously. The corrugation is about 0.2

nm for the topography and 1 nN for friction. (From Marti, O. et al. (1990), Nanotechnology 1, 141–144. With

permission.)

FIGURE 6.9 Set of atomically resolved images taken on HOPG with an Si

cantilever and a microfabricated tip.

The left images are raw data and the right images have been Fourier ﬁltered to show the different positions of the

maxima in the topographic and the friction images. The bottom image shows the relative positions of these maxima,

which are shifted with respect to each other. (From Ruan, J. and Bhushan, B. (1994), J. Appl. Phys. 76, 5022–5035.

With permission.)

the lateral force. By using Fourier expansion of the interaction potential, the normal and lateral forces

between tip and sample are calculated (Ruan and Bhushan, 1994b). For one lateral dimension (x-axis)

the argument elaborated on in this work can be summarized as follows: for a surface potential of type,

which describes, on the one hand, the atomic corrugation of the surface and, on the other, the decrease

of the normal force for increasing tip–sample distance, normal and lateral forces are calculated as

Therefore, minima and maxima of the normal and lateral forces are shifted by one quarter lattice spacing

with respect to each other. In the constant-force mode, topographic image is obtained by adjusting the

position of the sample to maintain a constant force. Hence, minima and maxima of the normal force

and of the topography coincide and are both shifted with respect to the lateral force. This explains

qualitatively the relative phase between the topographic image and the lateral force in the case of purely

conservative forces. For a detailed understanding of the lateral force and its relation to the normal force

and the topography, the exact shape of the interaction potential has to be known and other phenomena

such as the elasticity and deformation of the tip–sample contact (see Section 6.4.3.5) have to be taken

into account.

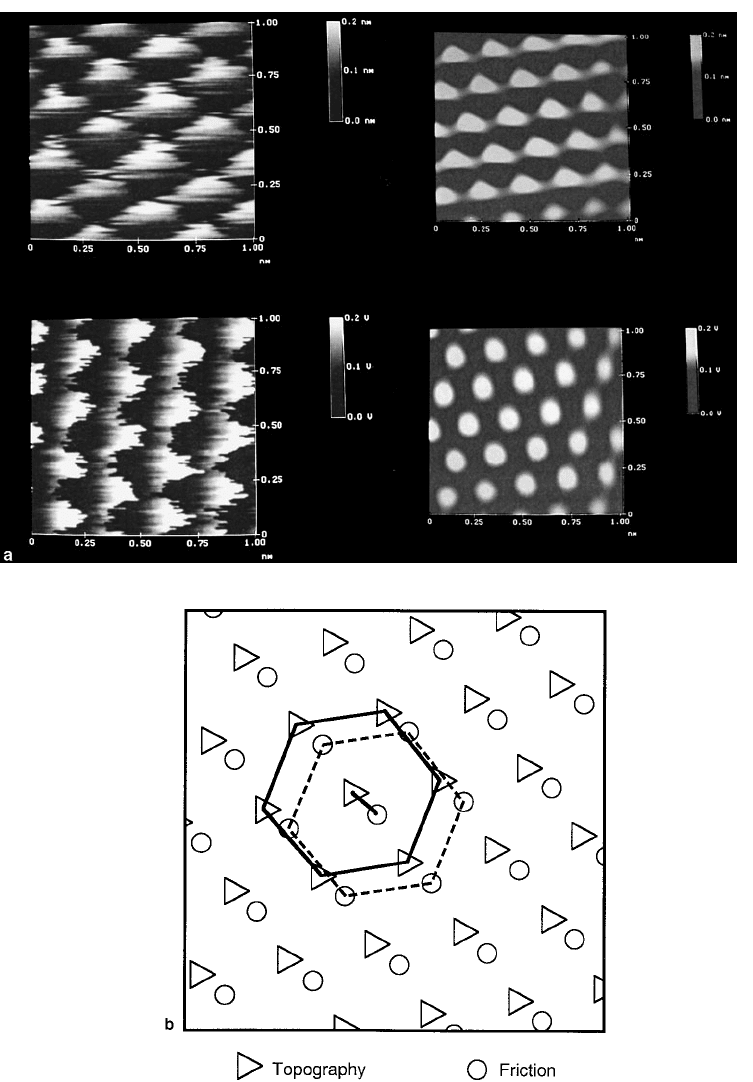
Two-dimensional images of the mica surface are shown in Figure 6.10. The images correspond to the

topography, the lateral force, and the normal force (from left to right). Essentially all images have the

sixfold symmetry of the hexagonal mica lattice, even though in the topographic image clearly some

directions are more pronounced. The lateral force image shows the typical stick-slip behavior and the

increase in lateral force at the beginning of each line discussed above. It is interesting that an effect due

to the friction force can be observed also in the topographic image. In fact, at the beginning of each line

some atoms seem to be “stretched.” This stretching is about one lattice constant long (0.52 nm). In

principle, two effects can be responsible for this stretching: bending and torsion of the macroscopic

cantilever at the beginning of the lateral force curve — this was discussed above — or the deformation

of the microscopic tip–sample contact (Colchero, 1993). In the case of the images shown, the displacement

of the cantilever was estimated to be only 0.1 nm and is thus too slight to explain the observed effect.

Therefore, the second option seems more probable. We would like to stress that this stretching is not

unique to the images shown but, on the contrary, quite common and is even seen in scanning tunneling

microscopy, where it is also explained by a sticking effect of the tip–sample contact (Albrecht, 1989).

Another interesting feature is seen in the image corresponding to the normal force, which shows rather

sudden peaks with the lattice periodicity. To understand this, we ﬁrst note that the topographic image

and the normal force image are complementary: if the feedback system does not appropriately correct

the height of the piezo (topographic signal), then the cantilever will be deﬂected (normal force signal).

Images taken in the constant-height mode show no contrast in the topographic image, in this case all

information is in the normal force image. Images taken in the constant-deﬂection mode, on the other

hand, should show no contrast in the normal force image, all information being in the topographic

image. Since feedback systems are never ideal, in this second case usually a small amount of structure is

visible also in the normal force image. However, in the case of the normal force image shown in Figure 6.10

the magnitude of the variation as well as its shape cannot be explained only by assuming as low feedback.

This is seen as follows: if a tip scans over a corrugated surface assumed to be approximately harmonic,

then the tip will “see” a harmonic variation of the surface height. Due to the ﬁnite bandwidth of the

VxzV kxe

surf

, cos ,

()

⋅

−

kV kxe

zzx

xxx

=−

∂

=⋅

()

⋅

=−

∂

=⋅

()

⋅

−

surf

cos ,

sin .

FIGURE 6.10 Two-dimensional images of the mica surface taken in air with an Si

cantilever and a microfabricated tip. Atomic resolution of the lattice

periodicity on mica is seen in all three images. The upper images represent raw data (in the case of the topographic image a plane has been substracted) and

the lower images have been Fourier ﬁltered to enhance the atomic periodicity. The left images correspond to the topography, the center ones to the lateral

force, and the right ones to the normal force. The scan range is about 5 nm.

feedback loop, the topographic and the normal force signal correspond to low-pass and high-pass

ﬁlteredimages of the real surface. Therefore, both images should again be harmonic. Their amplitudes

and their respective phase will depend on the time constant of the feedback system. The topographic

and the normal force images shown, however, have a different structure. While the topographic image

is indeed rather smooth — which can be explained by ﬁltering due to the feedback system — the normal

force image shows sudden peaks. These peaks are explained by an effect of the stick-slip motion. In fact,

if we assume that the tip sticks to some point on the surface until the lateral force exceeds some critical

value, whereupon the system becomes unstable and jumps to a new position, then it seems reasonable

that the normal force varies as the tip jumps into the new equilibrium position. This has important

consequences for the correct interpretation of images: if stick-slip occurs, the tip jumps over part of the

unit cell which accordingly is not imaged. Moreover, since the lattice spacing of the unit cell is reproduced

in the images, this further implies that the part of the unit cell which is imaged is stretched. A more

elaborate explanation for these sudden jumps has been proposed by Fujisawa et al. (1993) and will be

discussed in the next section. However, this different explanation does not modify the main message:

when stick-slip is observed, which is equivalent to a nonzero friction force and thus to energy dissipation,

then only a fraction of the unit cell is imaged, since the tip rapidly jumps over the other part of the unit

cell (Colchero, 1993). A more detailed description of this process will be presented in Section 6.4.3.3.

At this point again the question can be raised whether or not in the present case atomic resolution is

possible taking into account the ﬁnite contact radius. Taking again Equation 6.16 and assuming an Si

tip of about 30 nm radius, we estimate a contact radius of 2.5 nm, which is roughly the size of the image

shown and therefore again much larger than the periodicity resolved. Therefore, in this context, the high

resolution still has to be explained. Moreover, the above considerations regarding imaging within the

unit cell, although in principle important, are rather academic at the present point.

6.3.1.2 Two-Dimensional Stick-Slip

In the preceding discussion the frictional force was assumed to act only in the direction of the (fast)

scan. This is analogous to macroscopic friction, where the friction force is parallel to the relative velocity

of the sliding bodies. According to the simple model discussed above, the tip sticks to potential minima

on the surface until the lateral force built up due to the scanning motion of the tip exceeds the force

needed to shear the tip–sample junction. The potential minima were assumed to lie along the scanning

direction. A surface is, however, a two-dimensional structure and accordingly the potential minima do

not have to lie necessarily on the line deﬁned by the scan, that is, the line which the tip would follow if

no friction forces act on the tip. We will call this line the scan line. Depending on the symmetry of the

surface, the minima of the surface potential can be arranged in a very complex way. The tip, on the other

hand, can be deﬂected in principle in any direction, as was discussed in detail in Section 6.2.1.1. Therefore,

if the tip is scanned along an arbitrary line over a surface, the tip will not only stick to points exactly on

the scan line — in fact, for most scan lines there might not be any sticking points exactly on the scan

line — but will “look” for the most favorable sticking points off the scan line. Since the tip is then deﬂected

from the scan line, this induces lateral forces which are perpendicular to the direction of motion of the

tip and thus to the usual friction force. Therefore, for a real two-dimensional surface and a real SFFM

setup the tip motion is expected to be much more complex than the one-dimensional stick-slip motion

described usually. This two-dimensional stick-slip motion has been studied by Fujisawa et al. (1993) in

detail and published in a long series of papers (for a review, see Morita et al., 1996).

The ﬁrst question that arises in this context is how to detect this two-dimensional motion. With the

optical beam deﬂection method it is possible to detect simultaneously bending and torsion of a cantilever.

A lateral force causes a torsion of the cantilever if this force acts along the x-axis (see Figure 6.1 for the

convention used) and a bending if this force is along the y-axis (see Section 6.2.1.1). In the latter case,

the friction force can be separated from the normal force by taking the difference of the back and the

forward scan. Finally, we recall that in the case of typical rectangular cantilevers the force constants for

displacements along the x-axis and the y-axis are of similar magnitude, namely,

where c is the force constant for bending due to a normal force (see Equations 6.3, 6.5, and 6.8) and the

convention is used that the long axis of the cantilever is along the y-direction. Therefore, with the optical

beam deﬂection method and with appropriate cantilevers it is possible to detect simultaneously lateral

forces in both directions parallel to the sample (see Section 6.2.1.1).

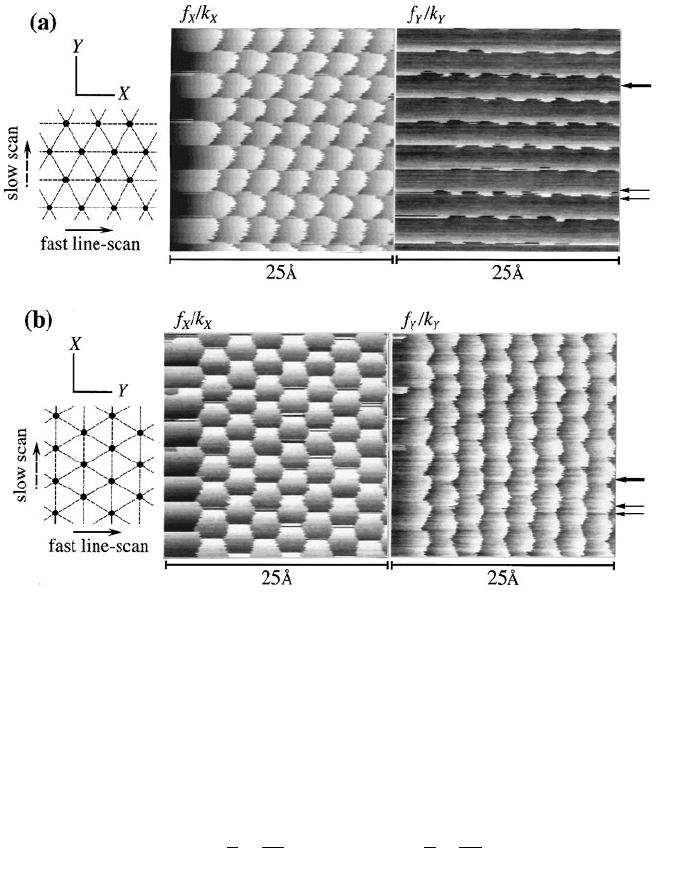
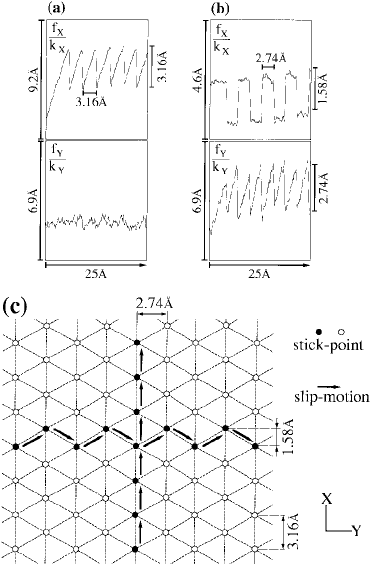
Figure 6.11 illustrates the two-dimensional stick-slip behavior for an Si

tip on an MoS

surface,

which is a layered material with a lattice periodicity of 0.274 nm. The upper images (Figure 6.11a)

correspond to the usual setup in SFFM where the fast scan is along the x-axis. The left image shows the

torsion of the cantilever — this is the image which is usually acquired as the friction image — and the

right image the bending of the cantilever. The lower images (Figure 6.11b) were taken with the fast scan

along the y-direction. Again, the left image shows the torsion and the right image the bending of the

cantilever. The fast scan in all images is from left to right. The ﬁrst and the last images are easily

understood: they reﬂect the typical one-dimensional stick-slip behavior. While the ﬁrst image is measured

FIGURE 6.11 Images illustrating the two-dimensional stick-slip behavior taken with an Si

tip on an MoS

surface.

The images labeled f

correspond to a twisting of the cantilever and the images labeled f

to a bending. For the

upper images (a), the fast scan is perpendicular to the cantilever (this is the usual imaging mode), and for the lower

ones (b) the fast scan is parallel to the cantilever (y-axis). The cantilever is aligned along the y-direction (see Figure 6.1

for the convention used). The thick arrows mark the positions of the sections corresponding to the lateral force curve

shown in Figure 6.14, and the thin arrows to lines from which the sections shown in Figure 6.12 were obtained.

(From Morita, S. et al. (1996), Surf. Sci. Rep. 23, 1–41. With permission.)

tors

tip tip

and

⋅













⋅=⋅













⋅ ,

in the usual torsion mode, the last image is measured by scanning along the cantilever. The other two

images cannot be explained within the one-dimensional stick-slip behavior. In particular, note the square-

wave shape of the third image.

To understand the two-dimensional stick-slip motion in detail, one should remember that the surface

can be described by a two-dimensional potential with a symmetrical arrangement of minima and maxima.

If no external forces act on an ideally sharp tip, then the last tip atom will move to the energetically most

favorable position which is a minimum of the tip–sample potential and the whole tip will correspondingly

be caught in this minimum. To move the tip from this minimum, a shearing force is needed. We consider

ﬁrst two special cases in which the tip is scanned parallel to the symmetry axes of the crystal which

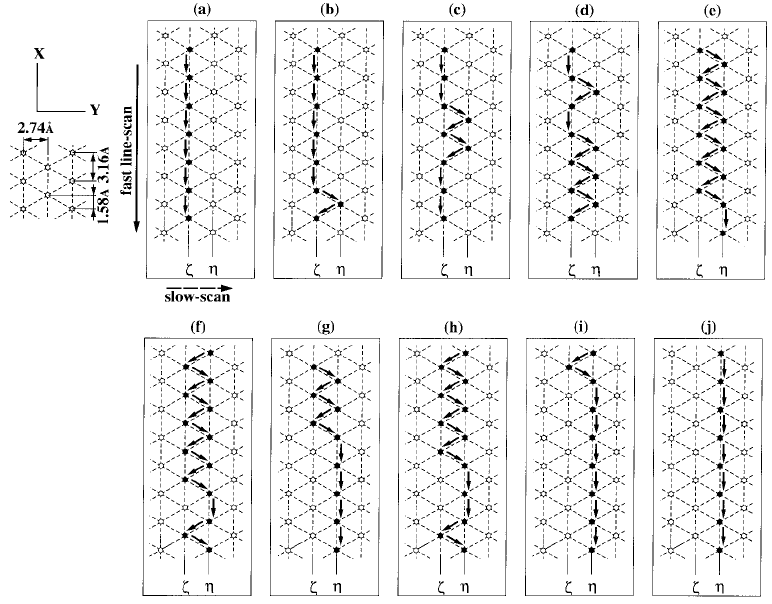
contains the potential minima (see Figure 6.13). In the ﬁrst case, the tip is moved on a line going through

these minima (for example, the lines ζ or η in Figure 6.13), and thus in an energy “valley.” The tip will

then stick in the nearest minimum until the shearing force built up during the scanning motion is high

enough so that the tip jumps into the next minimum along the scan line. Since the tip is caught in an

energy valley, only forces parallel to the scan line are measured and the stick-slip behavior is that of one-

dimensional stick-slip. Such a scan line is marked with a thick arrow in Figure 6.11a. The measured

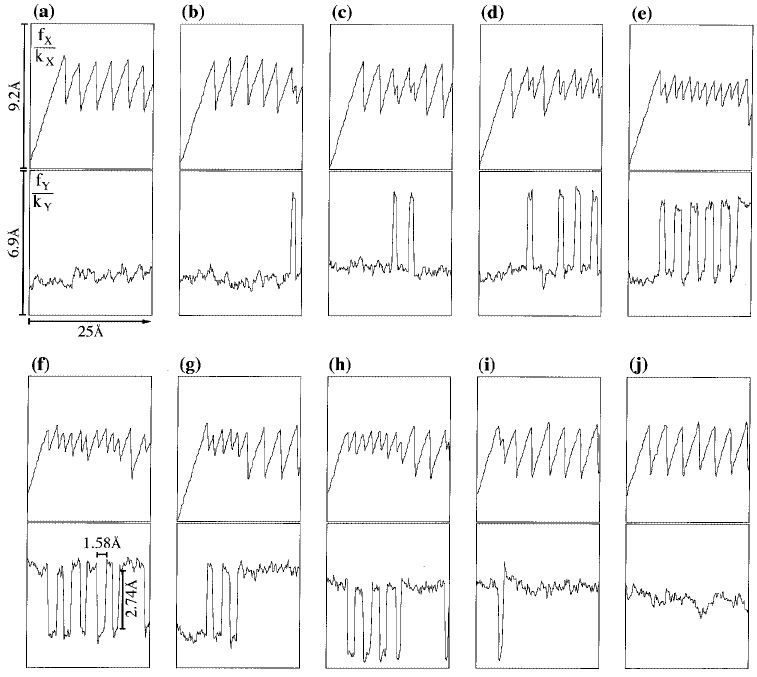
deﬂection of the cantilever corresponding to such a line scan is shown in Figure 6.12a and j, as well as

FIGURE 6.12 Signals corresponding to the line scans between the two thin arrows in Figure 6.11a. The signals

labeled f

correspond to the twisting of the cantilever and the signals labeled f

to its bending. Curves (a) and

(j) can be considered to show the “classical” one-dimensional stick-slip behavior: the cantilever is only twisted as the

tip is scanned perpendicular to the cantilever (x-axis) in an energy valley. (From Morita, S. et al. (1996), Surf. Sci.

Rep. 23, 1–41. With permission.)

in Figure 6.14a. Now let us consider a second case, where the tip is assumed to move between the lines

containing the potential minima (for example, a scan line halfway between the positions ζ and η in

Figure 6.13). The tip can then be considered to move over the maxima of the surface potential and the

minima lie on both sides of the scan line. If the cantilever is soft enough in the direction perpendicular

to the scan line, the tip will move to the nearest minimum off the scan line which induces a force

perpendicular to the scan direction. As the tip is scanned but still sticks to this point, a lateral force is

built up oriented along the scan direction (x-axis). This force increases linearly with the scanned distance,

while the lateral force perpendicular to scan line remains constant. When the (total) lateral force built

up during the scanning motion is high enough, the tip snaps into the nearest minimum, which now is

on the other side of the scan line. This behavior leads to a lateral force signal which is triangular-shaped

in the case of the component along the scan line and rectangular-shaped in the case of the component

perpendicular to this line (see Figure 6.12e and f). The intermediate cases where the tip is scanned neither

through the potential minima nor through the potential maxima are a combination of the two cases

discussed. Figure 6.12a to j shows the signals corresponding to scan lines between the thin arrows in

Figure 6.11a, and Figure 6.13a to j the motion of the tip reconstructed from these signals. Interestingly,

a region exists around the lines containing the potential minima where the tip is caught in the valleys

containing the potential minima, so that no jumps perpendicular to the scan line are observed. This is

seen in Figure 6.11, for example, around the position marked with the thick arrow (and also the corre-

sponding signals in Figure 6.14).

The cases described above assumed scanning parallel to the symmetry axis of the surface containing

the stick points. If the scan is perpendicular to this direction, essentially the same behavior is observed.

However, then the trivial case — scanning through the stick points — does not occur; therefore a

FIGURE 6.13 Two-dimensional stick-slip motion of the tip reconstructed from the signals shown in Figure 6.12.

(From Morita, S. et al. (1996), Surf. Sci. Rep. 23, 1–41. With permission.)

rectangular-shaped signal is always observed in the direction perpendicular to the scan line. This is seen

in Figure 6.14, which shows the signals for two different orthogonal scan lines and the corresponding

paths reconstructed from the measured motion of the tip.

In the images shown, the axes of the crystal, of the motion of the tip, and of the cantilever were aligned

with respect to each other. More speciﬁcally, the x-axis of the cantilever was parallel to the symmetry

axis of the surface containing the stick points and this axis in turn deﬁned one of the two perpendicular

fast-scan directions. If the scan is not aligned with respect to the crystal axis, the two-dimensional stick-

slip is even more complex than described above (Figure 6.15). In this case, the square wave signal

corresponding to the jumping of the tip between points on both sides of the central scan line is not ﬂat

as in the images before, but has a slope. This is seen as follows: let us assume that the tip sticks to some

point and that the sticking points are a long the x-axis. If the tip is now moved along a scan line which

is not parallel to the x-axis of the cantilever, then the tip will be moved away from the sticking point not

only in the x-direction, but also in the y-direction. This will induce lateral force components F

and F

which increase linearly with the scanned distance until the total lateral force built up during the scanning

motion is high enough to induce a slip into the next sticking point. Moreover, the values of the lateral

force corresponding to the stick-slip points are not all equal as in the previous case. However, they can

be calculated from the exact geometry of the experimental setup (Gyalog et al., 1995; Morita et al., 1996).

In conclusion, although the general two-dimensional stick-slip behavior can be very complex, it can

be understood within a simple model of the surface assuming that the potential minima of the two-

dimensional surface potential correspond to sticking points to which the tip adheres. It is evident that

FIGURE 6.14 (a) and (b) Friction signals measured in the two acquisition channels corresponding to twisting of

the cantilever (f

) and to bending of the cantilever (f

) shown for two different orthogonal scan lines. (c) Motion

of the tip reconstructed from the measured deﬂection of the cantilever. The signals shown correspond to the scan

lines at the positions marked by the thick arrows in Figure 6.11a and b. (From Morita, S. et al. (1996), Surf. Sci. Rep.

23, 1–41. With permission.)