Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

height, which demonstrates that the movement of these particles does not change the normal orientation

of the aliphatic chains. From this observation the shear strength at the interface between the substrate

and the LB ﬁlm can be determined. The contact area is given by the geometric dimensions of the sheared

island. In the case of Figure 6.23 the island area is 4900 nm

. The lateral force to shear the island is 5 nN.

A shear strength of τ = 1 ± 0.2 MPa is deduced.

Another class of boundary lubricants are ﬂuorocarbons. Direct comparison of ﬂuorocarbons and

hydrocarbons by SFFM on a nanometer scale provides a very effective way to study the lubricating

properties of these compounds. In one particular study, a 1:1 molar mixture of arachidic acid

COOH), AA, and partially ﬂuorinated ether carboxylic acid (C

–O–C

COOH), PFCEA,

complexed to a polymeric counterion (polyvinylpyridine), was deposited by LB technique. Monolayers

are formed on oxidized silicon (Meyer et al., 1992b) while bilayers are formed on hydrophobized silicon

(100) (Overney et al., 1992). Figure 6.24 shows a (2 × 2 µm

) area of a mixed bilayer of AA and PFECA.

Circular domains are surrounded by a sealike, ﬂat region. The step height is 1.6 nm, which corresponds

to approximately twice the difference between the longer hydrocarbons and the ﬂuorocarbons (≈1 nm).

The deviation from the expected value is possibly related to a certain tilt of the ﬂuorocarbons which

increases the step height. Therefore, the higher, circular domains are assigned to the hydrocarbons, while

the surrounding ﬂat regions are formed of ﬂuorinated bilayers. Within the circular domains, holes and

grooves of 5 nm depth are observed, which is consistent with the height of a bilayer of AA. The holes

reach all the way to the silica substrate, conﬁrmed by the large frictional forces recorded on these regions.

By contrast, the ﬂuorinated regions are free of holes. With higher forces, we observe that particles of

hydrocarbons are pulled out and sheared out of the scanning area while the ﬂuorocarbons remain

undeformed. Control ﬁlms of pure AA and pure PFECA show the same tendency. The hydrocarbon ﬁlms

have many defects and are easily deformed while the ﬂuorinated ﬁlms are rather uniform and cannot be

broken by the probing tip. The deformation conditions can be controlled by adjusting normal force and

scan speed. Therefore, nanometer lithography can be performed and “smileys” can be drawn, as shown

in Figure 6.25

The lateral force measurements indicate high friction on the substrate, intermediate friction on the

ﬂuorocarbon and small friction on the hydrocarbon domains. The ratio is approximately 10:4:1. At ﬁrst

sight the larger friction on the ﬂuorinated regions is surprising. From compounds such as Teﬂon (PTFE),

reduced friction is expected. However, it is known from surface force apparatus measurements that the

shear strength on ﬂuorinated LB ﬁlms is increased compared to the hydrogenated ﬁlms (Briscoe and

Evans, 1982). Nevertheless, ﬂuorinated ﬁlms are good boundary lubricants. They combine intermediate

friction with high resistance to rupture.

Finally, another interesting study on boundary lubrication is due to Salmeron et al. (1995). This group

prepared a alkythiol monolayer on an Au(111) surface. From electron-, helium-, and X-ray diffraction

FIGURE 6.23 Topographic , (a) and (c), and friction (b) and

(d), images of a double bilayer of Cd–arachidate. Scan size is

× 2 µm

, the loading force is 4 nN for the upper images and

16 nN for the lower ones. The total vertical scale in the topo-

graphic image is 24 nm and in the friction image 14 nN. No

damage is observed in the upper images at low loading forces.

At higher loading, however, small islands and ﬂakes are

sheared away. For example, the island indicated by the arrow

in image (a) is not observed in (c). (From Meyer, E. et al.

(1992), Phys. Rev. Lett. 69(12), 1777–1780. With permission.)

studies it is known that these thiols arrange in a × r30° structure with respect to the gold substrate.

This structure was also found by SFFM, which is noteworthy, since it shows that the structure of the

thiols remains stable in spite of the high tip–sample interaction which is typical for SFM and SFFM. As

the loading force was increased over a certain threshold value, which was of the order of a few hundred

FIGURE 6.24 SFFM images of a bilayer of a 1:1 mixture of PFECA and AA; the scan size is 4 × 4 µm

. The circular

islands in the topographic image (a) correspond to the hydrocarbons (AA) and the surrounding “sea” is composed

of ﬂuorocarbons (PFCEA). The friction image (b) shows low friction on the hydrocarbon phase, medium friction

on the ﬂuorocarbon phase, and high friction on the substrate. The ratio of the friction force on the different materials

is 1:4:10 and friction forces are in the nN range. (c) shows a schematic diagram of the arrangement of AA and PFCEA

on the hydrophobized silicon substrate. (From Overney, R. M. et al. (1992), Nature 359, 133–135. With permission.)

FIGURE 6.25 SFFM images of a monolayer of a 1:1 mixture of PFCEA and AA; the

scan size is 2.4

× 2.4 µm

. The topographic image (a) shows the circular islands of AA

which are also seen in Figure 6.24. If the forces applied with the SFFM tip are high

enough, “smileys” can be written. Image (b) shows the corresponding friction force

image. (From Meyer, E. et al. (1992), Thin Solid Films, 220, 132–137. With permission.)

3 3

nanonewtons, a transition takes place and the Au(111) lattice of the underlying surface is imaged (see

Figure 6.26). This transition is reversible: as the force was lowered about 100 nN below the critical force

of the ﬁrst transition, the image corresponding to the × r30° structure was recovered. The exact

values for the critical forces corresponding to the transitions varied from experiment to experiment and

depended mainly on the tip radius. Moreover, for tip radii larger than about 100 nm, these transitions

were not observed. The pressure at which the transitions occur was approximately constant, with a value

of about 1 GPa for the transition thiols–Au(111). This is a huge pressure, much higher than that at which

bulk gold yields and only slightly lower than the observed yield pressure of nanoscale gold contacts.

These observations are explained qualitatively as follows. At the critical pressure, the thiol chains are

pushed aside by the tip, but the head groups still remain chemically bound to the gold–substrate (see

Figure 6.26). Therefore, around the tip the thiol molecules are more densely packed, which results in a

radial inward pressure. This pressure can lift the tip again and restore the original conﬁguration if the

pressure is reduced. A more-detailed analysis is found in Salmeron et al. (1995).

Summarizing, we have discussed some applications of SFFM that are relevant for a better understand-

ing of lubrication. Adsorbed water can act as a lubricant also on a nanoscale. Films of one molecular

height are found to be effective lubricants. The observation that one bilayer of lubricant causes about

the same reduction of friction as two or more layers is of interest for the fundamental understanding of

boundary lubrication. Thiol monolayers on gold show stability up to very high pressures.

6.3.3 Nanocontacts

The experiments discussed previously made use of the imaging capabilities of the SFFM. SFFM and SFM,

however, are not limited to the acquisition of images. Essentially, an SFM and quite generally a scanning

probe microscope can be operated in two modes, the well-known imaging mode where the sample is

scanned, and a nonimaging mode where the decay of the interaction is studied by varying the tip–sample

distance over a ﬁxed location. The latter mode is sometimes referred to as the spectroscopic mode. In

this section, we will discuss the application of this mode to study the dependence of friction on the

normal force. For tribological studies, this mode is experimentally more complicated than in other cases,

since the tip evidently has to move in order to measure a friction force. Different experiment techniques

have been developed to measure friction at a point while moving the tip. On the one hand, several friction

images of the same region may be taken at different loads. By taking the friction value corresponding to

the same point in the different images, a friction vs. load curve is obtained. With this technique, friction

vs. load curves can be constructed at every point of the image (Meyer et al., 1992a). This method is

especially convenient if the sample is inhomogeneous and the variation of friction on different regions

of the sample is to be studied. Another method is to assume that the sample is homogeneous over a

certain area and take one friction image in which the loading force is increased or decreases for each new

FIGURE 6.26 SFM study of a C

alkanethiol monolayer at low

load (about 30 nN, left images), high load (about 300 nN, middle

images), and again low load (right images). The top images show

a schematic setup of the tip–sample system and the images in the

middle the acquired topographic signals. The lower images are two-

dimensional Fourier transforms of the corresponding topographic

images showing the relation between the alkanethiol monolayer and

the Au(111) lattices. (From Salmeron, M. et al. (1995), in Forces in

Scanning Probe Methods, pp. 593–598, NATO ANSI Series Kluwer,

Dordrecht. With permission.)

3 3

scan line (Hu et al., 1995). In this case from each line a friction value is obtained as the average friction

force along the line. The whole “image” therefore gives a friction vs. load curve. This method gives a

higher signal-to-noise ratio, since all the points along a line are averaged to obtain one data point on the

friction vs. load curve. Finally, modulation techniques (Yamanaka and Tomita, 1995; Colchero et al.,

1996a) as well as histogram techniques (Marti, 1993; Lüthi et al., 1995) have also been proposed.

In macroscopic friction, the relation between friction and load is usually linear and is expressed through

the well-known friction coefﬁcient: F

fric

= µ · F

. On the other hand, it is known experimentally that the

true contact area is also proportional to the loading force (Bowden and Tabor, 1964). Moreover, for

certain statistical distribution of roughness, this relation can be shown to be theoretically correct for

elastic contacts (Greenwood, 1992a,b). Therefore, on a macroscopic scale the linear relations

between loading force F

, friction force F

fric

, and contact area A hold. For low loads, we know from

different continuum models that for single asperity contacts, the relation between contact area and

loading force is not linear (see Section 6.4.2). The question arises, whether for nanoscale contacts the

last proportionality — F

fric

∝ A — is correct. This seems to be the case and correspondingly the friction

vs. load curve increases in a nonlinear way. Therefore, the notion of friction coefﬁcient is no longer well

deﬁned. Instead, it appears that shear strength is the fundamental parameter which describes friction in

nanoscale contacts (see discussion below).

The importance of studying frictional behavior with varying load was recognized already in the ﬁrst

SFFM experiments. Mate et al. (1987) found a linear relation between friction and load for a tungsten

tip on graphite, in contrast to what has just been discussed. Essentially, the same behavior was found on

other surfaces in a series of early SFFM experiments. Putman et al. (1995) studied the friction vs. load

curve in various environments. In ambient conditions they found a nonlinear relation, whereas in an N

or an Ar atmosphere, where the liquid ﬁlm covering tip and sample is reduced, a linear behavior is found.

Putman et al. propose that this dependence of friction on environmental conditions is due to the surface

roughness of the tip and to contaminants: in ambient conditions with about 55% relative humidity, the

liquid ﬁlm and possibly also other contaminants may smooth the tip surface, so that the tip forms a

single contact with the sample. If the liquid ﬁlm is absent, the contact may be due to microasperities

which lead to the same behavior as in macroscopic friction. The linear behavior of friction vs. load curves

is therefore considered to be an artifact. In a way, the tip–sample contact in this case is still “macroscopic,”

that is, at many ill-deﬁned contacts and not at one single and well-deﬁned contact. This study shows the

importance of having a well-deﬁned tip.

To separate the dependence of the friction on the area from intrinsic properties of the tip–sample

contact, it is useful to rewrite the friction as (Schwarz et al., 1996)

(6.13)

where S

is a frictional force per area, A

is the contact area, R is the tip radius, and E* is an effective

modulus of elasticity which is deﬁned in Equation 6.16. The last relation follows assuming a Hertzian

contact and a normal force F

which is corrected for the adhesion between tip and sample: F

= F

load

, with F

load

external loading force and F

the adhesion force between tip and sample. As discussed in

Section 6.4.2, other relations describing the load-area dependence can also be assumed. The frictional

force per unit area can be interpreted as the shear strength of the tip–sample junction, according to the

n fric

fric

∝

FSAS

fric

=⋅ =⋅π⋅

⋅













macroscopic model of friction by Bowden and Tabor (1964). If this shear strength is assumed constant,

then the friction is only determined by the contact area. Another simple relation is

where p is the pressure on the contact, which can be shown to follow from a thermally activated model

of the Erying type (Eyring, 1935; Briscoe and Evans, 1982). With this dependence, Equation 6.13 can be

written as

(6.14)

The ﬁrst term is proportional to the contact area, while the second is proportional to the normal force,

as in the case of macroscopic friction. Note that this conceptually simple linear dependence on normal

force is due to a nontrivial dependence of the friction on the area and on the shear strength.

In their experiments Schwarz et al. (1996) investigated the friction of C

on a GeS substrate as a

function of load. Interestingly, they found a different behavior on these two materials. While the friction

vs. load curve on the C

followed excellently an F

2/3

dependence, the friction vs. load curve on the GeS

substrate was approximately linear. For a good ﬁt to the experimental data on the GeS substrate, however,

the friction had to be described by both factors of Equation 6.14, which implies a complex relation.

In a similar experiment, Carpick et al. (1996a,b) found that the friction vs. load curve of a Pt tip on

mica was described almost perfectly assuming a constant shear strength and a load–area relation as

predicted by the JKR theory (see Section 6.4.2, Equation 6.20) of elastic contacts. To avoid possible

contamination, the experiments were performed in UHV, including the cleaving of the mica to expose

a fresh surface. To ensure a well-deﬁned tip shape, the tip was imaged using a faceted SrTiO

(305)

surface, as proposed by Sheiko et al. (1993), and found to be paraboloidal to a very good approximation.

To acquire one friction vs. load curve, images were taken by varying the load for every line, as discussed

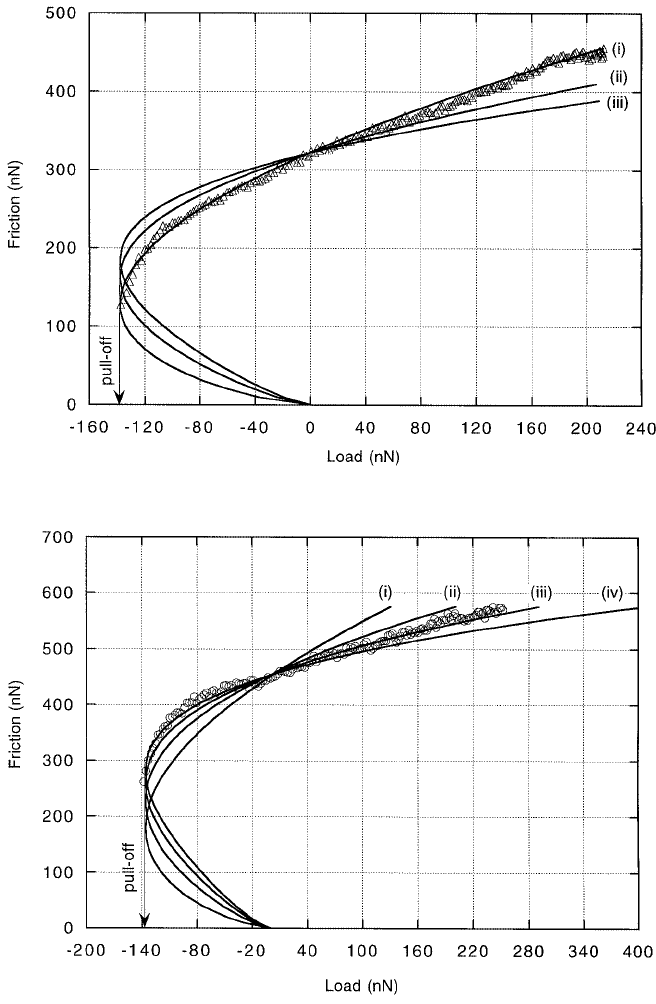
above. Typical friction vs. load curves are shown in Figure 6.27. The nonlinear behavior is evident. The

experimental data points have been ﬁtted to a contact area vs. load curve as predicted by the JKR theory.

Since the agreement between the ﬁt and the data is very good, the shear strength of the contact can be

assumed to be constant, so that the dependence on friction is determined only by the contact area.

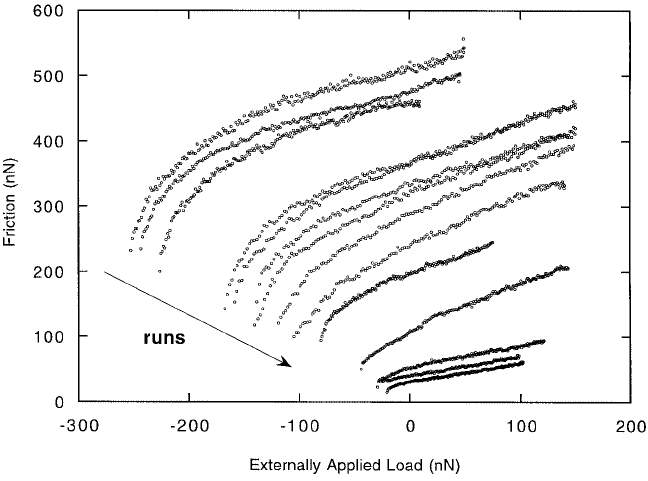
Another result of these experiments was that adhesion and friction decreased by more than an order

of magnitude during the experiments, that is, as more and more curves were acquired (Carpick et al.,

1996b). The authors checked that this decrease was not due to wear of the tip, which in any case would

increase the radius of curvature and thus also adhesion as well as friction. Every friction vs. load curve

could be ﬁtted by a JKR curve as described above (see Figure 6.28). From this, the authors deduce that

the decrease in friction is due to changes in the chemistry of the interface, which appears in the JKR

equation through the surface energy (see Equation 6.20). Since the experiments were performed in UHV,

not many mechanisms can explain this behavior. The authors propose either progressive graphitization

of hydrocarbon residues on the tip, or adsorption of K from the mica on the tip as possible explanations.

Nevertheless, it is quite surprising that even under UHV conditions, where contaminant layers are absent,

the friction of the tip–sample junction can be affected in such a dramatic way.

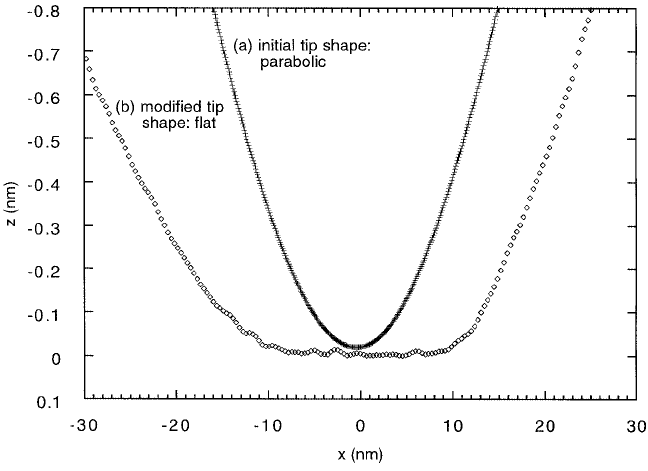
To investigate the effect of tip shape on the friction vs. load curve, Carpick et al. deliberately blunted

the tip and showed that unlike in the previous experiment the corresponding friction vs. load curve did

not follow the JKR area–load relation for a spherical tip in contact with a ﬂat sample (Carpick et al.,

1996a). As shown in Figure 6.27, an appropriate extension of the JKR theory for a tip with a general

shape y(r) = c · r

, however, could be ﬁtted almost perfectly to the experimental data. The best ﬁt

corresponded to the exponent n which was deduced from the measured tip shape by imaging a faceted

SrTiO

(305) surface. Therefore, although tip shape determines the friction vs. load curve in a nontrivial

way, if the tip shape is known its contribution can be taken into account.

Sp S p

()

=+⋅

α ,

FaFbF

nnfric

=⋅ +⋅

Similar results have been reported recenty by Schwarz et al. (1997). They show that even though the

absolute friction scales with the tip radius, its fundamental behavior does not vary for tip radii between

10 and 125 nm. In these experiments they also ﬁnd a shear strength which is independent of pressure.

The experiments described above were limited to the study of the frictional behavior of the tip–sample

contact. Experiments have also been performed to investigate other properties of tip–sample contacts

with scanning probe methods. More speciﬁcally, the formation of nanonecks has been investigated by

FIGURE 6.27

STM by measuring the current as a sharp tip is indented into a sample surface. The conductance of these

necks has been shown to vary in integer steps of the quantum resistance (Agraït et al., 1993; Pascual et al.,

1993). This can be explained in terms of the number of conductance channels which ﬁt in the minimum

cross section of the tip–sample contact. Other experiments have been performed to study the physics of

tip–sample contact not only with STM but also in combination with SFM (Rubio et al., 1996; Stalder,

1996). These studies suggest that during neck formation very strong pressures, compressive as well as

tensile, act in the neck and that substantial atomic rearrangement occurs, as predicted by molecular

dynamics simulations. Moreover, on a nanoscale materials seem to be much harder than on a macroscopic

scale (Agraït, 1996), which is in accordance with other studies (Bhushan and Koinkar, 1994) and can be

explained by the absence of defects in small nanometric volumes. These studies on the formation of

nanonecks have had up to now no direct consequences on atomic-scale tribology; we believe, however,

that both topics are very strongly related and that in the near future similar experiments will be done

which are indeed directly connected to tribology on a nanoscale.

6.3.4 Quartz Microbalance Experiments in Tribology

In SFM and SFFM the interaction between tip and sample is usually very strong and correspondingly

the pressures are very high. To study tribological processes at very low interaction and pressures, the

SFFM is at the moment not the ideal instrument. In this regime, the quartz microbalance (QCM) has

been applied successfully to study energy dissipation on an atomic scale. A QCM is essentially a crystalline

piece of quartz glass. Since this material is piezoelectric, if it is cut and segmented appropriately, it can

FIGURE 6.27 A: Friction vs. load curve of a Pt tip on a mica surface taken under UHV conditions. The curve

marked (i) corresponds to an area vs. load curve as predicted from the JKR theory for a spherical tip. B: Friction vs.

load curve of a Pt tip on mica after blunting of the tip. The curves shown corresponds to area vs. load curves according

to JKR theory for increasingly ﬂatter tip proﬁles: curve (i) is for a spherical or paraboloidal tip (z(r) ~ r

), curve (ii)

for z(r) ~ r

, curve (iii) for z(r) ~ r

, and curve (iv) for z(r) ~ r

. Each of these curves has been least-square ﬁtted

to the experimental data, the best ﬁt being for the shape measured experimentally and shown below. C: Experimentally

determined tip proﬁles (see text) showing the initial and ﬁnal tip shape which agree very well with the corresponding

friction vs. load curves. (From reference Carpick, R. W. et al. (1996), J. Vac. Sci. Technol. B 14(2), 1289. With

permission.)

be oscillated mechanically by applying a harmonic signal of correct frequency. Commonly a QCM is

used in vacuum chambers to measure evaporation rates: when material is deposited on the QCM, due

to the increment in mass its resonance shifts and from this shift the mass can be calculated (Lu and

Czanderna, 1984).

To study tribological processes, Krim and co-workers (Krim et al., 1991; Daly and Krim, 1996) use a

QCM which is driven in transverse mode, the motion of the QCM being then parallel to its surface.

Since a QCM is essentially a harmonic oscillator, three parameters determine its behavior: the resonance

frequency, a driving amplitude, and the quality factor Q of the resonance, which is a measure of how

much energy is lost during one oscillation. Typical values for the resonance frequency f

, driving ampli-

tude a

, and the Q-factor in the experiments to be described are f

≈ 8 MHz, a

≈ 20 nm, and Q ≈ 10

respectively.

A metal ﬁlm — usually Au or Ag — is evaporated prior to the experiment as the substrate for the

friction measurements. The surface roughness of these ﬁlms was measured by STM, X-ray reﬂectivity,

and liquid nitrogen adsorbtion measurements. Since the estimated sliding distance of the ﬁlms on the

substrate is of the order of 2 nm and therefore considerably smaller than the typical grain size, the effect

of surface roughness is assumed to be small. Experiments are performed in a vacuum chamber in a liquid

nitrogen bath. A noble gas — Kr or Xe — is brought into the chamber and adsorbs under equilibrium

conditions onto the metal surface on the QCM. At 77.4 K these ﬁlms are known to adsorb as one- or

two-monolayer-thick ﬁlms. The ﬁrst monolayer adsorbs ﬁrst as a liquid, which then solidiﬁes as the

partial pressure of the gas is increased and the monolayer is compressed.

During an experiment, a ﬁlm is deposited by slowly increasing the partial pressure of the gas, while

the shift in resonance frequency and the variation of the Q-factor is measured. The shift in resonance

frequency δf is proportional to the (areal) mass density ρ (unit: Kg/m

) deposited on the QCM, and the

FIGURE 6.28 Series of friction vs. load curves of a Pt tip in contact with mica taken under UHV conditions. As

more and more curves are acquired, the pull-off force as well as the friction force decreased. Each of these curves

can be ﬁtted to a JKR curve. The reduction of adhesion and friction observed in this experiment is not due to a

change in tip shape as in the previous ﬁgure, but due to a reduction in surface energy and shear stress which is caused

probably by variations of the structure or chemistry of the interface. (From reference Carpick, R. W. et al. (1996),

Langmuir 12(3), 3334–3340. With permission.)

variation of the Q-factor is a measure of the energy dissipated by the presence of the ﬁlm. From these

measured quantities, the so-called slip time,

of the ﬁlm is calculated (Krim and Widom, 1988). This slip time can be interpreted as a characteristic

time until friction stops the relative motion of the ﬁlm, i.e., a damping time. Since the total mass is

proportional to the frequency shift, the slip time can be considered to be normalized with respect to the

number of atoms which have been adsorbed. Assuming a friction force proportional to the sliding velocity

of the ﬁlm (Stokes law), it can be shown that 1/τ is proportional to the mean energy dissipated per atom

(Krim et al., 1991). The friction itself can be written in terms of the shear stress S needed to slide the

ﬁlm over the surface:

where ρ is the areal mass density and v the velocity of the ﬁlm. This relation implies a friction which is

proportional to velocity and therefore of Stokes-type as is typical for gas or liquid ﬂow. In fact, the

coefﬁcient ρ/τ can be interpreted as interfacial viscosity. The velocity dependence of the friction has been

conﬁrmed experimentally (Krim et al., 1991).

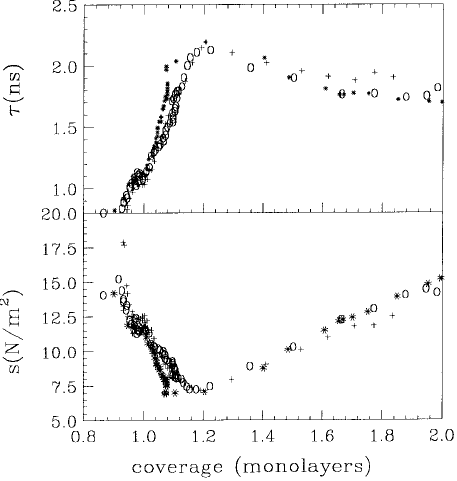
Figure 6.29 shows the result of an experiment where xenon is adsorbed on a silver (111) surface (Daly

and Krim, 1996, 1997). The slip time τ decreases until the ﬁrst monolayer is completed. As this monolayer

is compressed and solidiﬁes, the slip time increases; therefore, the friction of the ﬁlm decreases (not

shown). The same behavior is observed for Kr on Ag and Au (Krim et al., 1991). This is interesting and

counterintuitive because it means that, unlike in macroscopic friction, a solid noble gas ﬁlm on a metal

substrate slides easier than a liquid one. The ﬁlms are thus “slippier when dry” (Krim, 1996). Similar

results have been obtained theoretically by Cieplak et al. (1994), who attribute the friction to phonon

processes within the ﬁlm–substrate system (see also Solokoff, 1990). Other possible contributions to the

friction are due to the electronic resistance felt by the electrons in the metals as they are inﬂuenced by

the moving ﬁlm (Levitov, 1989; Persson, 1991, 1993). The experiments by Krim and co-workers, including

some recent results (Daly and Krim, 1996, 1997), seem to indicate that phonon processes are mainly

responsible for the friction observed. This is in accordance with friction in SFFM, which can also be

interpreted in terms of phonon creation (see Section 6.4.3.3). The underlying mechanism would then

be similar even though the range of shear stress is almost ten orders of magnitudes different.

6.4 Modeling of an SFFM

In the preceding sections, many experiments have been described which we believe are relevant to the

processes governing friction on an atomic scale. We have tried to explain most results with simple

arguments along the way. No deeper knowledge of theoretical work in nanotribology has been assumed.

In this section, the attempt will be made to explain some of the addressed experiments in more detail

and to describe basic concepts involved in SFM and SFFM. Since SFM, SFFM, and nanotribology in

general are part of a still very young ﬁeld, many phenomena are still far from being fully understood,

both from an experimental as well as from a theoretical point of view. The fundamental question in

tribology is, of course, how energy is dissipated. Essentially, two different mechanisms have been pro-

posed, one involves phonic and the other one electronic excitation. Very much has also been learned

from molecular dynamics simulations as well as from ﬁrst principles calculations. To study tribological

phenomena, these latter approaches are very difﬁcult and complex, due to the large number of atoms

()

1 Q

Sv=⋅

involved in tribological processes: while the main interaction might involve only a few atoms on each of

the sliding surfaces, the elastic deformation reaches much farther into the two interacting bodies and

ﬁnally, the volume into which elastic waves — that is, phonons — can be scattered is even larger.

Therefore, very different length scales are typically involved in tribological processes even if interaction

is through a small, well-deﬁned nanometer contact. Similar arguments lead to the conclusion that also

very different timescales can be involved. Recently, mixed atomistic and continuum models have been

proposed (Tadmor et al., 1996), but the situations treated up to now with this approach are very simple.

Molecular dynamics and surface physics are treated in detail in this book in Chapters 11 and 3 by Harrison

et al. and by Ferrante and Abel, respectively. Essentially, the scope of this section is to describe the processes

encountered in SFFM. In particular, we will try to address the following main questions in SFFM:

What is the reason for the high apparent resolution?

What is the mechanism for the stick-slip motion? and

How and where is energy dissipated?

We will limit the present section to simple models which, although much less precise, still explain some

fundamental aspects of friction on an atomic scale (Zhong and Tománek, 1990; Tománek et al., 1991;

Colchero and Marti, 1995; Colchero et al., 1996b; Gyalog et al., 1995). These models can be considered

an extension of a molecular model of friction proposed by Tomlison (1929).

6.4.1 Resolution in SFFM

Mostly, the total interaction of tip and sample in SFM can be calculated by adding all the interactions

between inﬁnitesimal volumes of tip and sample. Here, a similar approach will be presented, which

however will assume that the interaction takes place between the surfaces of tip and sample (for a similar

FIGURE 6.29 Top: Slip time vs. coverage for a xenon ﬁlm deposited on a silver surface for three different surfaces.

One monolayer has been deﬁned as 5.970 atoms/nm

, the spacing of the compressed monolayer, and the slip time

is normalized with respect to this point. Bottom: Corresponding shear stress for the xenon ﬁlm on the silver surfaces

as a function of coverage. This shear stress is the force per unit area required to slide the ﬁlm at a constant speed of

1 cm/s (the order at which the ﬁlms are moving). (From Daly, C. and Krim, J. (1996), Phys. Rev. Lett. 76(5), 803–806.

With permission.)